识别低渗油藏甜点的试井解释体系及其应用
2014-06-27廖新维赵晓亮李东晖陈晓明
叶 恒, 廖新维, 赵晓亮, 李东晖, 陈晓明
(中国石油大学(北京) 石油工程学院, 北京 102249)
0 引言
中国低渗透油藏储量资源丰富,是目前油田增储上产的主要阵地,开发潜力巨大[1].比如,1990年探明低渗透油层地质储量为21 214×104t,占当年总探明储量的45.9%; 1995年探明低渗透油层地质储量增加到30 796×104t,占当年总探明储量的比例高达72.7%[2,3].随着低渗、特低渗油藏在油藏开发中发挥着越来越重要的作用,如何识别甜点已经成为开发的重要问题.
试井技术是一种探测油层的直接方法[4],也是在油气田勘探中了解地层特征的一种被广泛使用的技术[5].对于低渗、特低渗油藏,利用试井技术时,特别需要注意多解性的问题[6].因此,本文建立了一套试井解释体系,降低了试井解释的多解性,并阐述了利用该体系来识别低渗透油田甜点的原理及方法.
1 基本原理与方法
1.1 单井拟合
测试井都采用不稳定试井方法.首先,对单井的不稳定试井测试资料进行初步地拟合,在此阶段仅以拟合曲线为目标.如图1所示,通常在进行低渗油藏试井解释时,油井大多经过压裂,低渗透油藏深层压裂产生的裂缝大多是垂直裂缝,表现出裂缝特征[7].但由于测试时间的限制,双对数曲线的特征响应不明显,多种模型都可以拟合.因此,降低多解性,已成为亟需解决的问题.
基于此目的,本文建立了一套基于时空尺度的“三维”试井分析技术.该方法充分利用了试井曲线在时间和空间的三维尺度上的交互性,降低了试井解释的多解性,获得了准确的井筒和地层参数.同时,还把信息源的分布、信息的再现和再生有机地结合起来了[8].
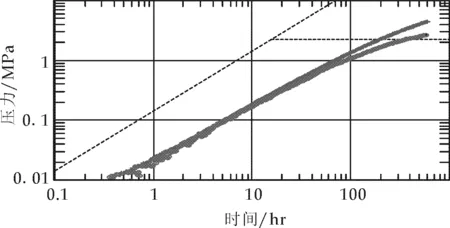
图1 低渗透油藏压力恢复双对数曲线
1.2 利用“三维”试井技术确定合理的解释模型与解释结果
1.2.1 筛选典型井组
为保证试井解释精度,首先需要筛选出典型井组进行分析.其筛选标准如下:
(1)至少应有一口井在时间尺度有两年的测试资料,以便分析动态特征. (2)井组中至少有注水井的测试资料,以便规定外推地层压力上限.
(3)井组中至少应有3口油井的测试资料,以便充分进行空间尺度的交互验证.
(4)试井测试资料对应的原始双对数曲线,压力导数曲线和压力曲线最好要出现“分叉”,防止仅对井储段进行解释[9].
对于没有分叉的双对数曲线,数量不能超过一条,且同年井组中要有其它井的测试资料,用于判断不分叉双对数曲线解释结果的正确性.
1.2.2 利用基于时空尺度的“三维”试井分析技术对典型井组进行分析
对经上述过程筛选出的典型井组,优先进行分析.以井组为单位,对试井资料进行单井时间尺度上的分析,对比不同年份相同井的测试资料,进行合理性地分析,以确定该井动态变化最可能性的结果与原因,从而调整相对应的解释模型与结果.
随后,对井组中同一年相似测试时间的井进行分析,在空间尺度上验证试井分析的合理性,以调整相对应的解释模型与结果,识别并删除无效的试井测试曲线,确定最终结果.其流程见图2所示.
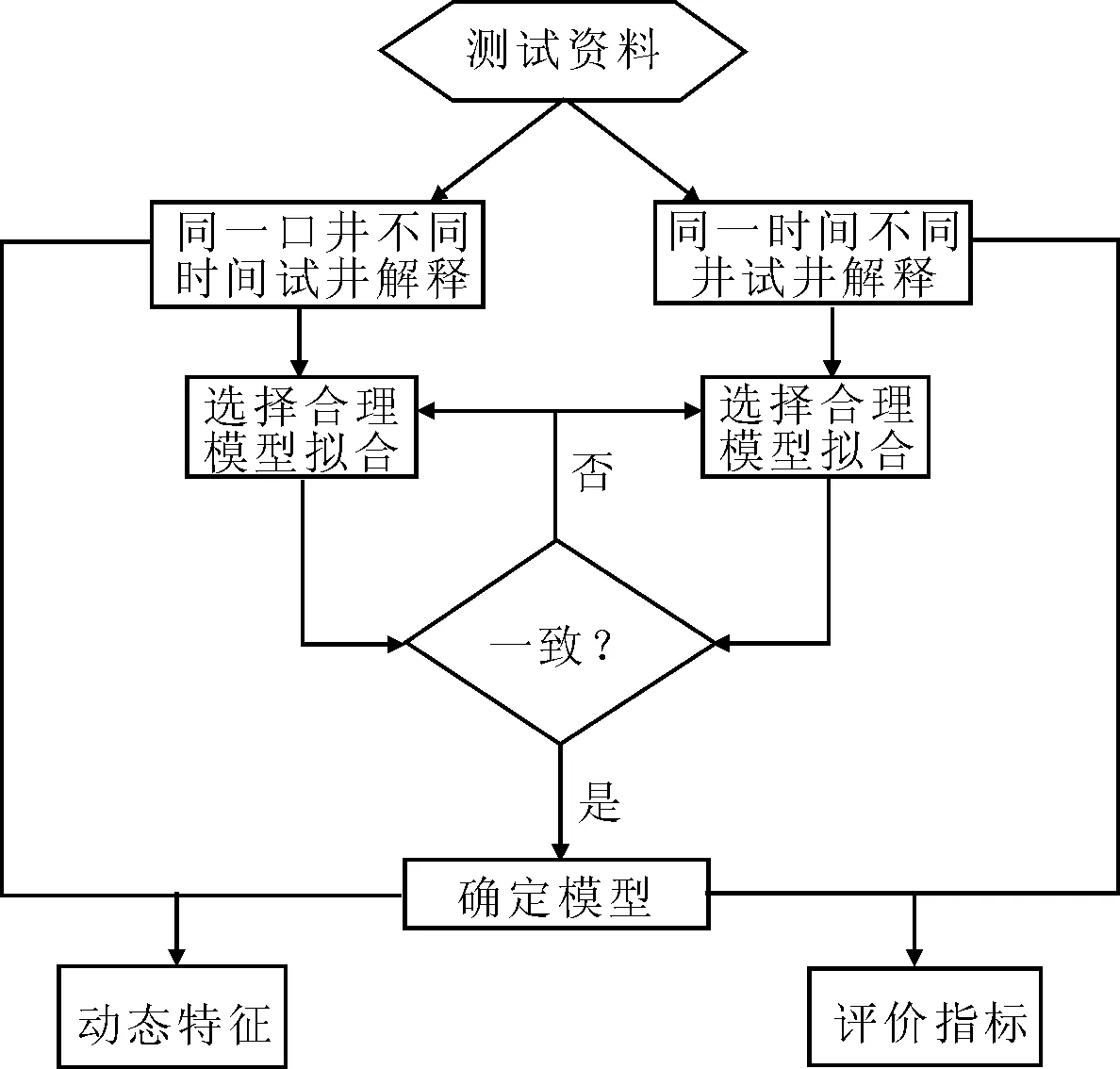
图2 基于时空的试井分析技术流程
1.2.3 利用基于时空尺度的“三维”试井分析技术对所有井组进行分析
由于对典型井组采用了基于时空尺度的试井资料解释分析技术,从而可以确定井组对应的储层性质的大致范围.通常情况下,相邻井组间物性差异不大,以此为基础,依次对所有测试井组进行基于时空尺度的试井解释分析,最终确定所有井次的解释结果.并结合数值模拟技术拟合出理论曲线,分析实测曲线出现的原因.
1.3 用克里格插值方法计算储层物性的空间分布并提出甜点
对于点的插值方法有很多种,包括泰森(Thiessen)多边形方法、反距离加权法、移动拟合法、样条函数、克里格(Kriging)插值法等[10].
考虑到实测有效厚度的不准确性,插值过程中没有对渗透率插值,而是对相近时间的地层系数进行插值.对于采用径向复合模型的解释结果,采用外区地层系数,是为了更好地反映储层基质性质.由于地层系数在空间上的连续性变化是非常不规则的,所以不能用简单的平滑数学函数进行模拟.
克里格插值方法着重于权重系数的确定,从而使内插函数处于最佳状态,即对给定点上的变量值提供最好的线性无偏估计.此外,克里格插值在几种方法中具有最好的外推能力,以及最为广泛的使用范围[11],而常常应用于地学统计中.因此,本文对空间分布状况的研究采用克里格(Kriging)插值法.
对于普通的克里格方法[12],一般公式为:
其中,Z(xi)是n个样本点的观测值,Z(x0)为待定点值,λ为权重 ,权重由克里格方程组决定.
其中,C(xi,xj)为样本点之间的协方差,C(xi,xo)为样本与插值点之间的协方差,μ为拉格朗日乘子.插值数据的空间结构特征由半变异函数描述,其表达式为:
其中,N(h)为被距离区段分割的试验数据对数目.
根据插值对象的特性,选取适当的理论变异函数模型.指数模型中插值对象的相关性在无穷远处才消失[13],显然不能符合我们地层系数的实际情况.故本文选用球状模型,其特点是空间相关随距离的增长而逐渐衰减,当距离达到某一值(变程)后,空间相关消失[14],符合我们对地层系数非均质的认识.
在插值的过程中,由于水井周围的储层遭到了长期的冲刷,水井周围的渗透率远大于正常值,并不能还原真实的地层系数.为保证插值的精度,在插值过程中忽略了水井的数据.最后,用不同的颜色标注不同井组地层系数的情况,颜色越深,地层系数越大.再通过插值图识别出可能的甜点位,并用生产数据进行验证,最终提出甜点位置以指导生产.
综上所述,本文建立了一套完整的识别低渗油藏甜点的试井解释体系.其流程图见图3所示.
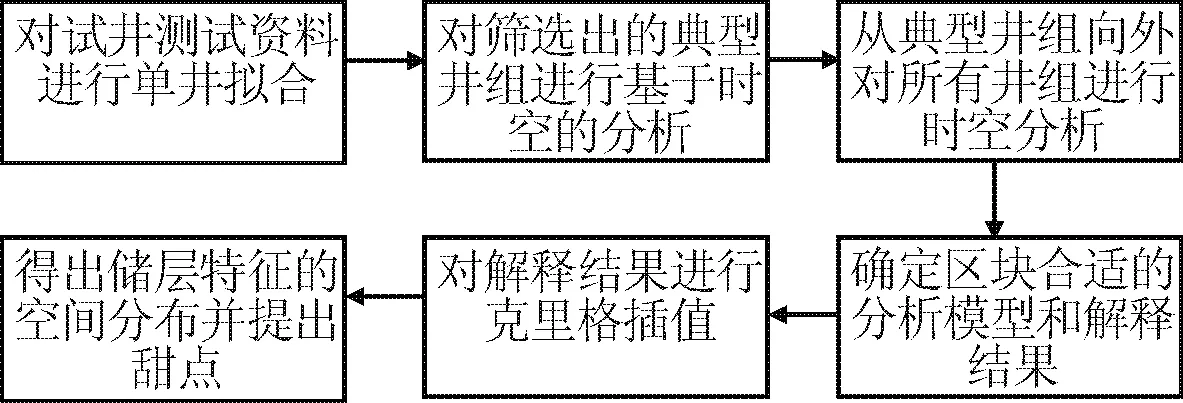
图3 试井解释体系流程
2 油田应用
长庆油田某作业区于2008年开始规模建产.为了更好地认识储层参数和空间分布特征,在2011年和2012年两年期间,对该作业区进行了多达72口井次的试井测试.将建立的试井解释体系应用于该作业区,其最终预测的甜点处与实际情况较为吻合.
首先,对单井进行各种可能性模型的拟合,如X90-89井,分别用三种模型进行拟合,如图4所示.
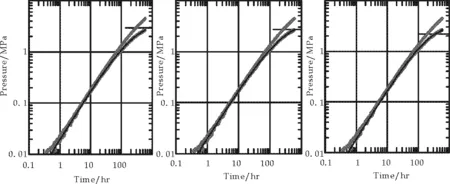
图4 分别使用均质、有限导流和径向复合模型拟合
其次,通过筛选标准,筛选出了X93-100、X93-102、X87-96和X93-80等四个典型井组.现以X93-100井组为例,说明建立的基于时空尺度的试井分析技术的使用.
对X93-100井组,进行了五口井次的测试,分别是X93-100井(2011年),X94-100井(2011年、2012年),X93-99井(2012年),X92-99井(2011年).其井位图如图5所示.
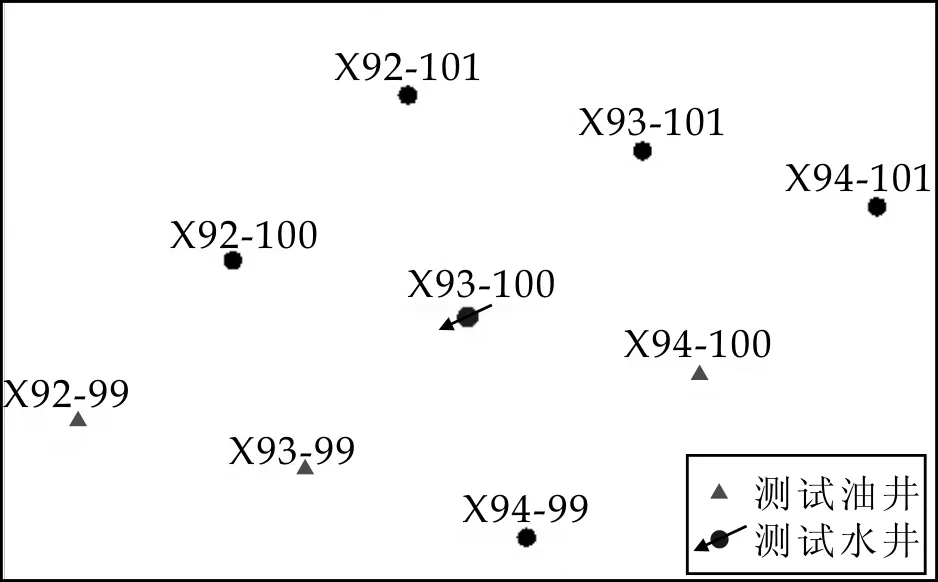
图5 X93-100井组井位图
先对中心水井X93-100进行拟合,外推地层压力为20.31 MPa.因此,在对油井的测试资料拟合过程中,外推地层压力一般不会高于20.13 MPa.
然后,对X94-100井进行单井时间尺度上的分析,如表1所示.对2011年试井曲线选用不同模型拟合时,外推压力和储层的渗透率差异较大,并且2012年测试对应的储层物性和外推压力好于2011年的情况,不符合注采比从1.75下降到0.78的客观事实.考虑到未分叉曲线的多解性,这两年曲线拟合结果的正确性,有待从空间的角度上来进行验证.对应的双对数曲线如图6所示.
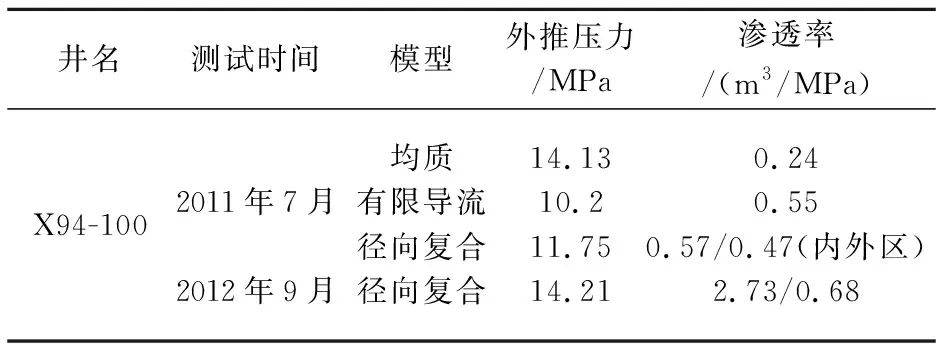
表1 X94-100井解释结果
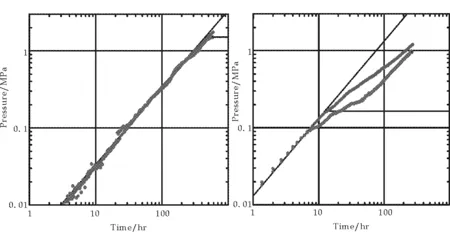
(a)2011曲线 (b)2012曲线图6 X94-100对应的双对数曲线
如上所述,由于低渗油藏测试数据的局限性,使得在时间尺度上的分析结果的多解性得不到很好地解决.因此,需要进行基于空间尺度上的试井测试资料解释.对X93-100井组,在2012年对X94-100井和X93-99井进行了试井测试.其测试资料对应的双对数曲线如图7所示.
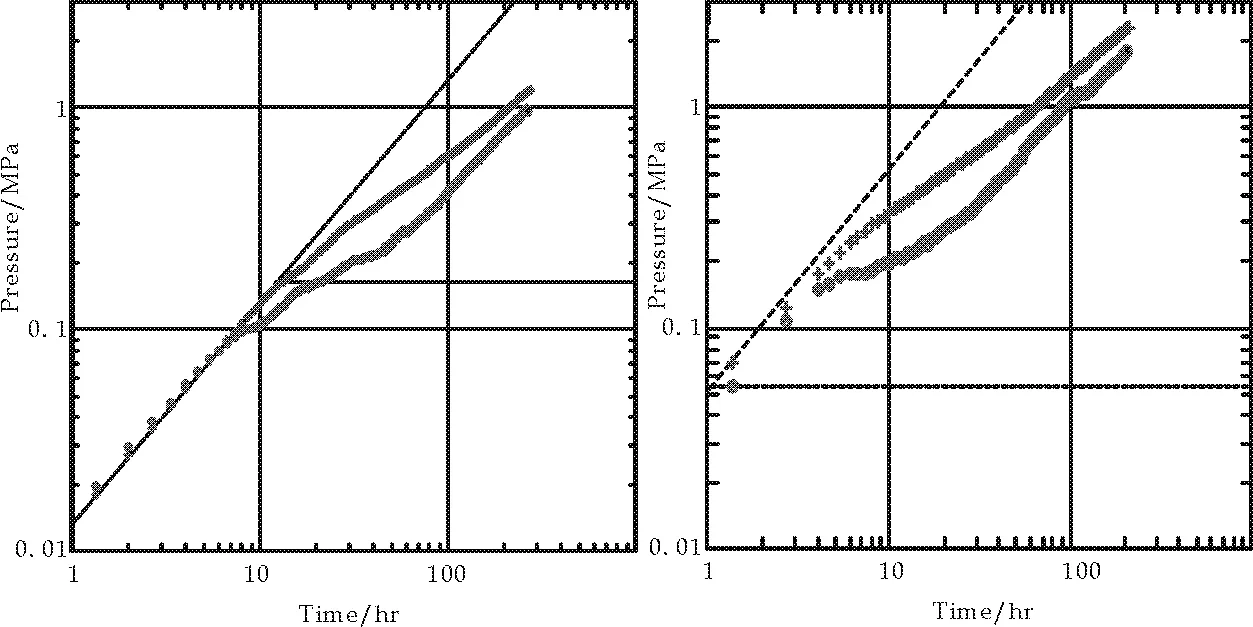
(a)X94-100井 (b)X93-99井图7 2012年试井双对数曲线
对X93-99井的测试资料进行拟合,应用径向复合和裂缝有限导流能力模型都能得到较好地拟合.由于该作业区原始地层压力为13.27 MPa,并且压力水平保持较好.因此,对于X93-99井,径向复合模型拟合的外推压力更符合实际情况.
另外,从空间尺度上来看,同一时间在空间上相近的两口井的测试资料解释结果中的储层性质应该接近.X94-100井和X93-99井的解释结果,当选用径向复合模型时,外推压力和储层渗透率(外区渗透率)最为接近.因此,选用径向复合模型对X94-100井和X93-99井的解释结果较为可靠.
2012年的测试井拟合结果如表2所示.

表2 井组2012年测试资料试井解释结果
最后,对余下的X92-99井进行解释分析.从空间尺度,参考邻井X93-99井的解释结果,对X92-99井试井结果进行调整分析,结果见表3所示.
比较X92-99井与X93-99井的解释结果,随着测试年的增加,压力减少,渗透率也相应地减少,符合我们的客观认识.将2011年X92-99井的解释结果与2011年X94-100井的解释结果进行对比分析,X94-100井的解释结果压力或者渗透率太小,不合理.经过多次调参,对X94-100井在2011年的测试数据,仍然不能得到合理的解释结果.因此,删除X94-100井在2011年的解释结果,以便保证后续插值的精度.
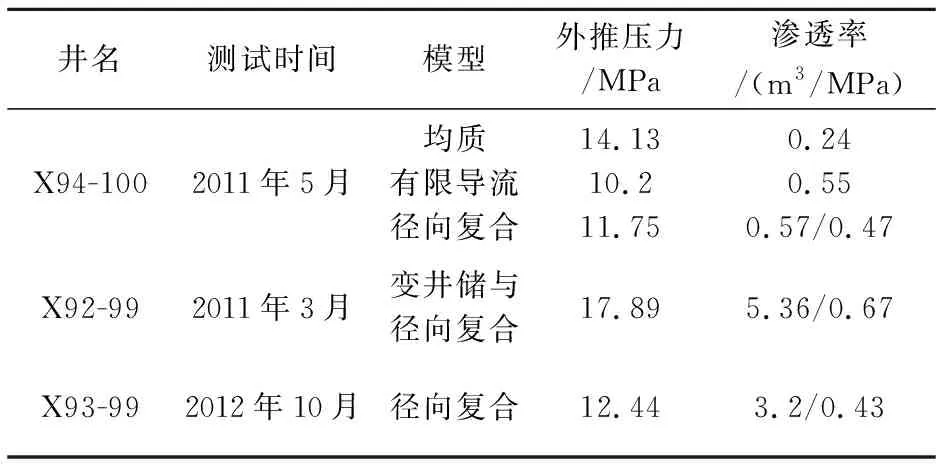
表3 井组2011年测试资料试井解释结果(2012年临井作为对比)
当确认了基本模型和大概的储层物性参数以后,对试井曲线再次进行调参,增大井组中井之间相关性和解释结果的合理性.最终的拟合结果见表4所示.
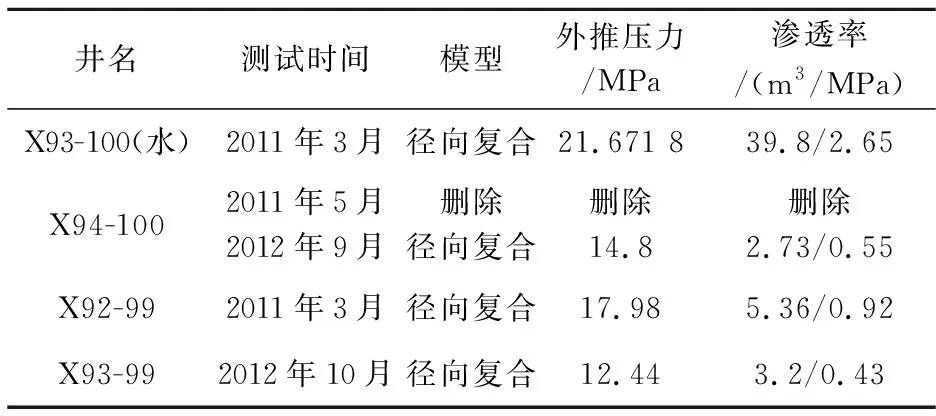
表4 X93-100井组最终解释结果
最终拟合曲线见图8所示.

(按照表4井排列顺序)图8 最终拟合曲线
在完成典型井组的试井解释分析后,以拟合结果为基础,按照就近原则,依次完成其它井组试井资料的解释分析,从而最终对所有井次试井资料进行分析,以确认拟合结果.
该区块油井都经过压裂,但是通过对井组的分析,基于拟合程度和物性参数,多数测试油井采用了径向复合模型而非裂缝模型.为分析造成这一现象的原因,利用数值模拟技术模拟了压裂工艺造成的试井理论曲线[15],如图9所示.
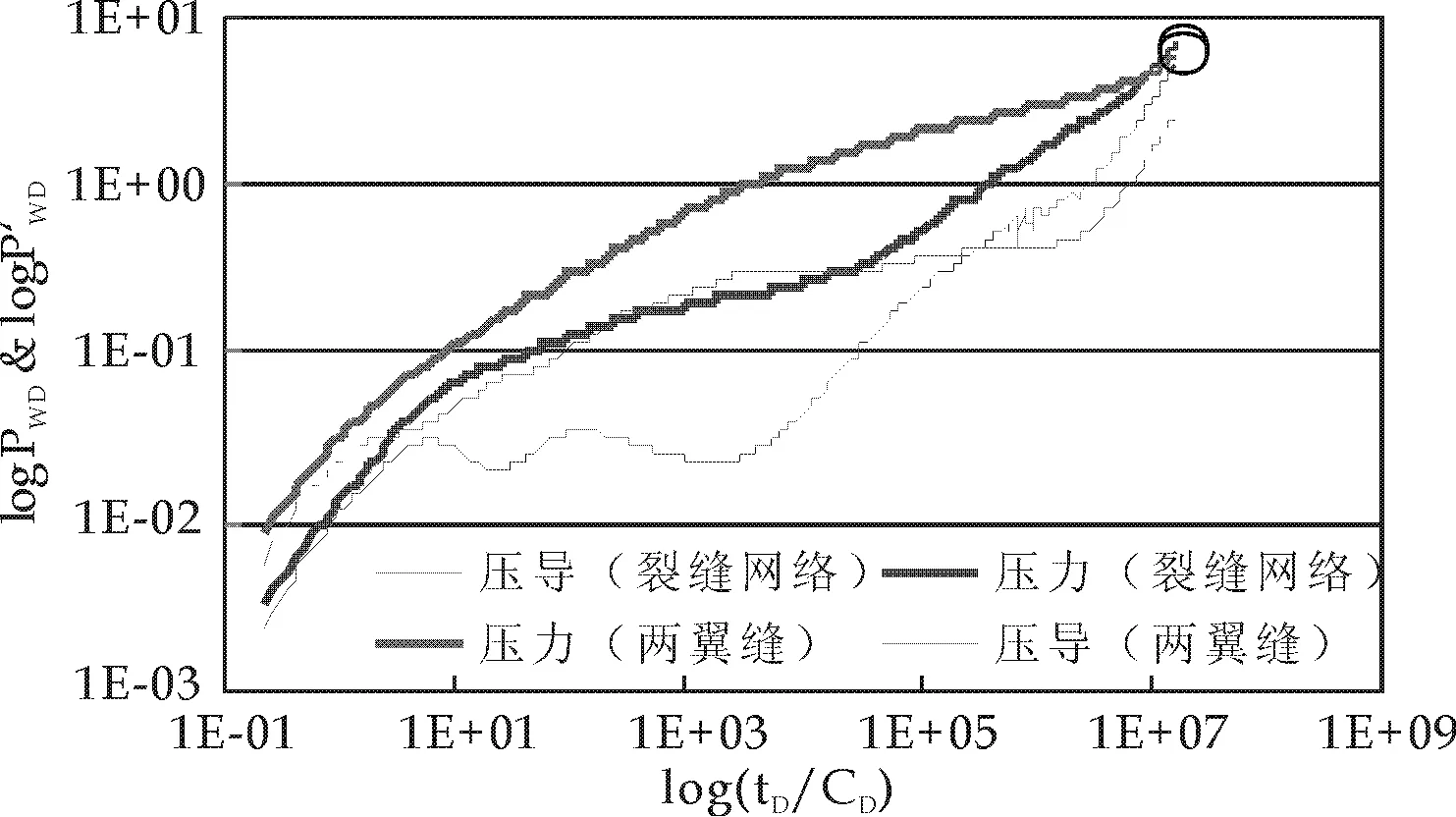
图9 数值模拟理论曲线
对比数模理论曲线和实测曲线,实测曲线介于理论曲线表现出的两翼缝和裂缝网络特征响应之间,这可能是由于在压裂过程中使用滑溜水等工艺,导致压裂过程中在主缝的基础上形成了部分次生缝[16].虽然没有形成裂缝网络,但形成了一个近似改造内区的特征响应.
分别对2011年和2012年该区块试井测试资料的解释结果,进行克里格插值,如图10所示.
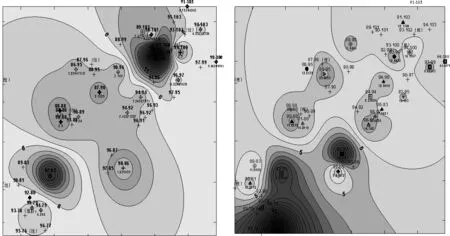
图10 地层系数空间分布插值
由图10可知,在作业区上中下三个区域可能存在高地层系数区.结合工作制度,中部高地层系数区的出现是由于采油井转注,形成了局部排状注水,长期注水冲刷导致物性好,这是人为的情况,所以被排除.
而剩下的两个高地层系数区则可能是相应的甜点.为了验证结论,通过分析生产动态数据,发现甜点处井的产量都比较大.因此,通过上述试井解释体系,较为成功地预测了区块的甜点位置,对后续工作具有一定的指导意义.
3 结论
(1)建立了一套完整的识别低渗油藏甜点的试井解释体系.实例分析表明,该体系具有很好的实用价值.
(2)基于时空尺度的“三维”试井解释技术能够很好地降低试井解释的多解性,排除无效的测试结果,保证了试井解释的精度.
(3)在基于时空尺度的试井解释技术的基础上,利用克里格插值方法可以有效地评价甜点的位置.这为低渗油藏确定主力产区,布新井等提供了参考依据.
[1] 王光付,廖荣凤,李江龙,等.中国石化低渗透油藏开发状况及前景[J].油气地质与采收率,2007,14(3):84-89.
[2] 同登科,葛家理.分形油藏非达西低速渗流模型及其解[J].大庆石油地质与开发,1996,15(3):18-23.
[3] 同登科,葛家理.分形油气藏不稳定渗流时关于续流和表皮效应的影响[J].天然气工业,1997,17(1):55-57.
[4] 汪宏伟,何鹏举,刘军峰,等.低渗透油藏试井技术应用[J].油气井测试,2012,21(2):26-29,76.
[5] 廖新维,沈平平.现代试井分析[M].北京:石油工业出版社,2002:1-4.
[6] 刘能强.实用现代试井解释方法[M].5版.北京:石油工业出版社,2002:23-24.
[7] 黄成江.试井资料在低渗透油藏评价中的应用[J].油气地质与采收率,2011,18(2):83-86,116.
[8] 吴洪彪,刘立明,陈钦雷,等.四维试井理论研究[J].石油学报,2003,24(5):57-62.
[9] 姚榛榛.低渗透气藏试井分析方法及应用研究[D].大庆:大庆石油大学,2006.
[10] 朱求安,张万昌,余钧辉.基于GIS的空间插值方法研究[J].江西师范大学学报(自然科学版),2004,28(2):183-188.
[11] 翟进乾.克里金(kriging)插值方法在煤层分布检测中的应用研究[D].太原:太原理工大学,2008.
[12] 刘湘南,黄 方,王 平.空间分析原理与方法[M].2版.北京:科学出版社,2008:194-206.
[13] 蔡元菲.快速三维克里金插值方法研究及实现[D].成都:电子科技大学,2013.
[14] 张小艳,谭 勇.变差函数球状模型的自动拟合与实现[J].物探与化探,2010,34(2):253-257.
[15] H Wang,X Liao,H Ye.The performance evaluation of old well after SRV in ordos basin tight oil reservoir[C]//Trinidad & Tobago Energy Resources Conference.Port of Spain,Trinidad and Tobago: Society of Petroleum Engineers,2014:1-13.
[16] 王文东,赵广渊,苏玉亮,等.致密油藏体积压裂技术应用[J].新疆石油地质,2013,34(3):345-348.
