变系数EV模型在人民币汇率中的应用

王 雁， 张德生， 王丽辉， 荀新新

(西安理工大学 理学院， 陕西 西安 710054)

0 引言

汇率是两种货币之间兑换的一种比率，在世界经济中发挥着重要的作用.它不仅会影响国家的宏观调控，而且会影响其经济结构.汇率波动是产生汇率风险的重要因素，而汇率风险所产生的经济损失严重程度取决于未来汇率在受险时间内的变动幅度，这就要求对未来汇率走势进行准确的预测.

在汇率研究的方法中,时间序列分析法是应用最广泛的.一般地，在时间序列分析法中经常会遇到高维数据，为解决这一问题学者们提出了变系数模型，因为变系数模型既继承了非参数回归的稳健性特点又保留了线性模型的直观性和易解释性，其中测量误差EV模型目前应用比较广泛.Datta, auri S.，Rao，J.N.K.，Torabi，Mahmoud[1]等人用误差线性回归模型来研究小范围客观的贝叶斯估计；Loannis Andrianakis[2]，Andrea Spoto[3]对于EV模型的研究效果作了分析；崔恒建[4]采用调整的加权最小二乘法估计结构关系EV模型的变系数；刘强、薛留根[5]考虑了在响应变量随机缺失情形下的线性EV模型；杜理论[6]提出了协变量带测量误差的非参数回归分析的估计方法；何其祥[7]研究了当响应变量为区间数据时的EV线性回归模型；尤太林[8]从正交回归分析的角度讨论了EV模型的参数估计；罗鹏首[9]讨论了在数据带有测量误差的情况下，研究EV模型中参数估计；李春会、朱永忠[10]根据最小二乘法对结构EV模型进行参数估计，并证明了基于数据剔除线性模型与均值漂移模型的参数估计的等价性；靳志同等人[11]提出异方差线性EV模型的T-型回归估计模型；王秀丽[12]考虑半参数可加线性EV模型中参数检验问题，提出了经验似然比检验统计量；田瑞琴、薛留根[13]考虑了纵向数据线性EV模型的变量选择.而关于自适应变系数EV模型的研究还比较少，周丽[14]在李泽华[15]的变系数EV模型系数参数核估计的基础上研究了自适应变系数EV模型的估计及性质，并通过计算机模拟加以研究.

本文主要将文献[14]中自适应变系数EV模型应用在人民币美元汇率预测的研究中，并与其它几种变系数模型的实证结果进行比较.

1 自适应变系数EV模型

1.1 自适应变系数EV模型基本框架

自适应变系数EV模型[14]的形式为：

(i=1,2,…,n)

(1)

其中：

xi=(xi0,xi1,…,xip)T；ui=(ui1,…,uip)T

g(ui)=(g1(ui),…,gp(ui))T;u=βTx;

Xi=(Xi1,…,Xip)T;

1.2 自适应变系数EV模型中的参数估计

对于模型(1)中的参数估计步骤如下：

以估计g0(·)为例来说明.

第一步：设定系数函数g0(·)取它的数学期望，这时就将非参数模型变为标准的线性模型.

令b0=E(g0(u))，μ0=E(xi0)=E(Xi0)；

α=μ0b0;b=E[g(u)];

bT=(b1,…,bp)T=(E[g1(u)],…,E[gp(u)])T；

则模型(1)变为标准的线性模型：

(2)

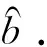
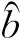
其中w(u)=w(u,u1,u2,…,un)为一列权函数，即

K(·)为R1上的概率密度函数，hn(hn>0)为窗宽，满足w(u)≥0.

(3)

将u=βTx代入到(3)中得出g0(βTx)的第二步估计为：

第五步：对于参数β的估计采用文献[16]中的方法.

2 自适应变系数EV模型实证研究

2.1 样本选取

本文选取人民币与美元兑换的中间价2006年1月至2013年5月共89个数据，其中2006年1月至2012年12月，共84个数据用于拟合建立模型，2013年1月至2013年5月，共5个数据进行预测.数据来自国家外汇管理局http://www.safe.gov.cn/wps/portal/sy/tjsj_hlzjj_inquire.

2.2 数据处理及平稳性检验

为了检验原始数据序列{xt}的平稳性，利用单位根(ADF)检验，如表1所示.

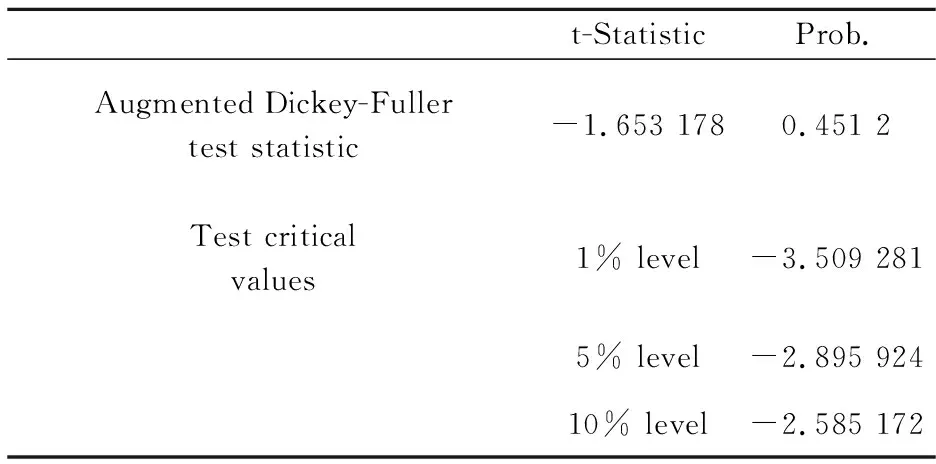
表1 原数据的平稳性检验

若假设显著性水平α=0.05，由表1可知，概率值0.451 2>0.05，说明原始数据序列不平稳.

通过试算，考虑{xt}取对数的二阶差分序列，即预处理的序列为{yt}：

yt=100×(logxt-2×logxt-1+logxt-2)

这里xt为每月的即期汇率，xt-1为前一月的汇率，xt-2为前两月的汇率，yt为预处理后的序列.

利用Eviews5.0单位根检验方法，对预处理后序列{yt}平稳性检验，其检验结果如表2所示.

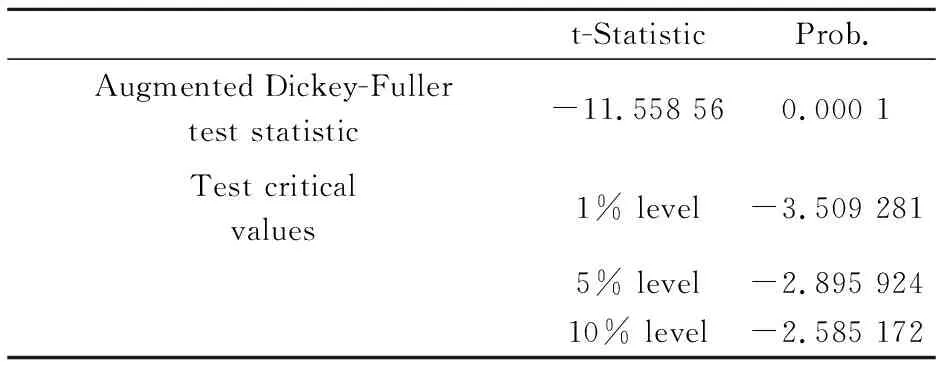
表2 预处理序列的单位根检验

在显著性水平为α=0.05的假设下，由概率值0.000 1<0.05，说明预处理序列平稳，可以进行建模.其中原始数据图如图1所示，预处理后的序列图如图2所示.

图1 原始数据图

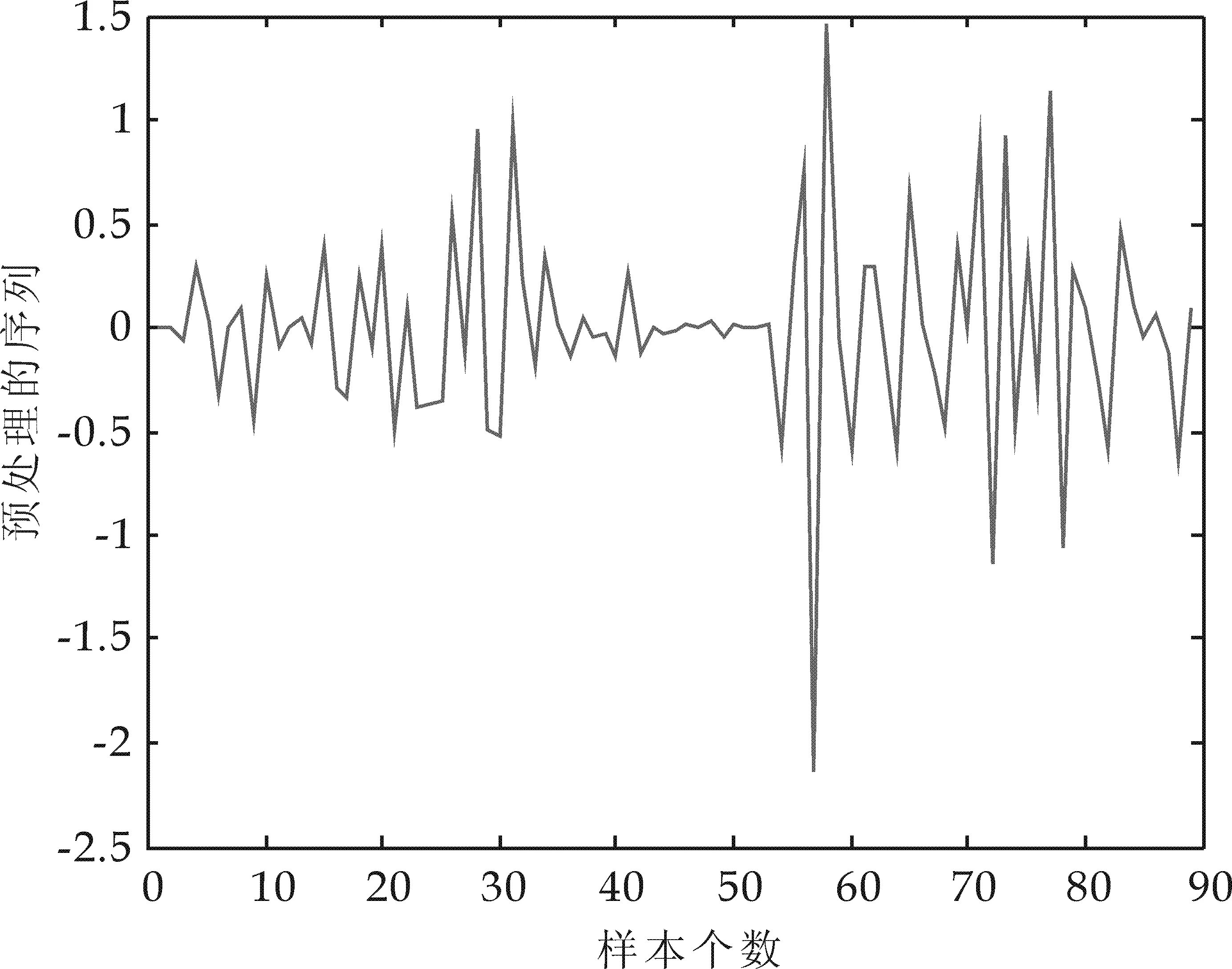
图2 预处理序列图

2.3 模型的建立及预测

建立模型之前首先要确定模型的带宽和滞后阶数，滞后阶数采用Cross-Validation方法来确定，取滞后阶数的上界K=10，经过Matlab7.0编程，得出cv(k)值在k=1时达最小；另外，选取最优核函数K(u)=0.75(1-u2)+，采用交错鉴定法确定最优窗宽.选用局部线性估计，通过Matlab7.0编程得出最佳带宽h=0.2.则所建立的自适应变系数EV模型的表达式如下：

(t=1,…,n)

(4)

其中xt、xt-1分别表示人民币美元汇率经过平稳化处理后的第t个与第t-1个数据，(xt0,xt-1)的值不能精确观测，其观测值相应的为(Xt0,Xt-1)，且E(εt,et-1)=0,Cov(εt,et-1)=σ2I2，σ2>0.

根据所建模型(4)，经过Matlab7.0编程可以得到人民币美元汇率2006年1月～2012年12月的拟合值，并将数据还原，然后将所得的拟合值和原始数据进行比较，结果如图3所示，由此可知，拟合值与真实值比较接近，拟合效果好.

图3 自适应变系数EV模型的拟和效果

用所建的自适应变系数EV模型对人民币美元汇率进行预测前，还需要检验模型的稳定性.本文采用χ2检验对残差序列进行平稳性检验，由Matlab7.0编程计算得出该模型残差序列的χ2检验的统计量值为15.372，明显小于显著性水平为0.01时的χ2检验的临界值23.209 3，说明残差序列通过了白噪声检验，该模型稳定，可以用来进行预测，并将结果还原，预测结果如表3和图4所示.

表3 自适应变系数EV模型的预测结果 (单位：人民币元)

图4 自适应变系数EV模型预测结果

2.4 几种变系数模型的预测比较

为了进一步说明自适应变系数EV模型的优越性，我们用函数系数自回归(FAR)模型和自适应函数系数自回归(AFAR)模型分别对2013年1月至2013年5月，共5个数据进行五步预测，并画出三个单模型的五步预测结果对比图，如图5所示.

图5 三个模型预测对比图

由图5可知,自适应变系数EV模型的五步预测效果并不明显，为了便于更好的说明，我们通过计算平均绝对误差(MAE)和均方误差(MSE)比较其拟合效果和预测效果如表4和表5所示.

表4 拟合误差的比较(单位：人民币元)

表5 预测结果的比较(单位：人民币元)

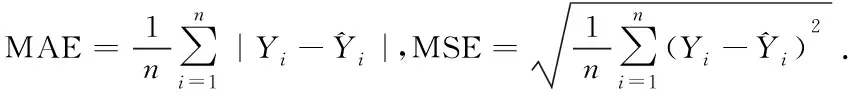
从表4与表5可以看出，在三个变系数的单模型中，FAR模型拟合和预测效果最差；AFAR模型次之；由于在自适应变系数EV模型中结合了变系数模型和误差向量模型的优点，从而使得拟合效果最好，其预测精度也优于其他两种模型.

3 结论

本文将自适应变系数EV模型在原有计算机模拟试验的基础上应用在人民币美元汇率的研究中，最后将FAR模型、AFAR模型和自适应变系数的EV模型在人民币美元汇率中的预测效果进行比较，由于在自适应变系数EV模型中考虑了误差向量，从而使得该模型有较高的预测精度.

[1] Datta Gauri S.,Rao J.N.K.,Torabi Mahmoud.Pseudo-empiric-al Bayes estimation of small area means under a nested error linear regression model with functional measurement errors[J].Journal of Statistical Planning and Inference,2010,140(11):2 952-2 962.

[2] Loannis Andrianakis,Peter G.Challenor.The effect of the nugget on Gaussian process emulators of computer models[J].Computational Statistics & Data Analysis,2012,56(12):4 215-4 228.

[3] Andrea Spoto,Luca Stefanutti,Giulio Vidotto.On the unidenti-fiability of a certain of skill multi map based probabilistic kno-wledge structures[J].Journal of Mathematical Psychology,2012,56(4):248-255.

[4] 崔恒建．变系数线性EV模型参数的调整加权最小二乘估计及其渐近性质[J]．系统科学与数学，2007，27(1)：82-92．

[5] 刘 强，薛留根．缺失数据下线性EV模型中参数的经验似然置信域[J]．数学的实践与认识，2008,38(24)：147-151．

[6] 杜理论，基于核实数据EV模型的非参数回归函数估计[D]．天津：南开大学，2010．

[7] 何其祥．区间数据下EV线性回归模型修正的广义最小二乘估计[J]．系统管理学报，2011，20(4)：480-484．

[8] 尤太林.EV模型的正交回归分析[D]．贵阳：贵州财经学院，2011．

[9] 罗鹏首.函数系数部分线性EV模型的局部多项式估计[D]．上海：华东师范大学，2012．

[10] 李春会，朱永忠．基于均值漂移模型的线性结构EV模型异常点分析[J]．重庆理工大学学报(自然科学)，2012，26(5)：101-104．

[11] 靳志同，任晴晴，赵玲玲．异方差线性EV模型T-型估计在确定面波震级与地震矩关系式中的应用[J]，防灾科技学院学报，2012，14(2)：50-53．

[12] 王秀丽．半参可加部分线性EV模型中参数的经验似然比检验[J]．山东师范大学学报(自然科学版)，2013，28(3)：1-4．

[13] Tian Rui Qin，Xue Liu Gen.Variable selection for the linear EV model with longitudinal data[J].Chinese Journal of Applied Probability and Statistics,2013,29(3):246-260.

[14] 周 丽.自适应变系数EV模型的估计及性质[D]．长沙：湖南师范大学，2009．

[15] 李泽华.变系数EV模型系数参数的核估计[D]．长沙：湖南师范大学，2006．

[16] 范剑青，姚琦伟.线性时间序列[M]．北京：高等教育出版社，2005：243-248，256-261．