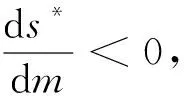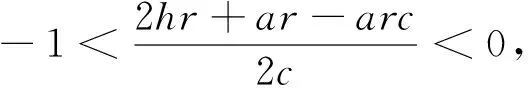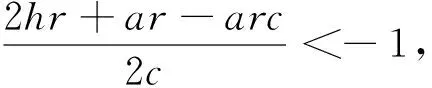庇护效应下一类改进的Holling-Tanner反应扩散捕食模型的定性分析
2014-06-27岳宗敏白云霄蔡永丽
岳宗敏, 白云霄, 曹 慧, 蔡永丽
(1.陕西科技大学 理学院, 陕西 西安 710021; 2.中山大学 数学与计算科学学院, 广东 广州 510275)
0 引言
捕食-食饵系统是生物界最常见的两种群关系,建立数学模型[1,2]研究种群关系是生物数学研究的重要内容,相关结果已有不少[3-7], 关于Holling-Tanner系统以及基于比率依赖的Holling-Tanner系统已有了广泛的研究[8-12], 文[13]研究了具有Smith增长改进了的Holling-Tanner系统:
(1)
其中食饵种群在时刻t的密度为x(t),并假设该种群的增长规律满足方程
(2)
2009年陈凤德[14]等人研究了一定比例的食饵进入避难所的Leslie-Gower型捕食-食饵系统
(3)
其中mx(t)表示时刻t时一定比例的食饵被庇护空间保护,并且m∈(0,1).通过使用特征根法,分析了避难所效应对该系统全局稳定性的影响,得到无论怎样改变庇护空间中食饵的数量,系统(3)的稳定性始终不发生改变,即避难所效应不影响系统的稳定性.
受以上论文启发,本论文所要研究的系统如下:
(4)
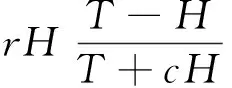
H(x,y,0)>0,P(x,y,0)>0,(x,y)∈Ω.
1 系统的持久性
定理1[15]对于t>0,系统(4)所有解是非负的,并且满足
(5)
定义如果存在正常数M0=M0(H0,P0),使得对于系统(4)所有满足初值H0>0,P0>0的解(H,P)都有
(6)
成立,则称系统(4)的是持久的.
定理2若(1-m)(1+c) 证明:设(H,P)是系统(4)的一个正解,可知 由抛物方程比较原理可知,当时(1-m)(1+c) 故对于任意ε>0,存在T∈(0,+∞),使得H(x,y,t)∈Ω×(T,+∞),有H(x,y,t)≥μ-ε. 由系统的第二个方程可知 由抛物方程比较原理,令ε→0,可得: 由 可知,当系统(4)满足条件ar+hr+m-1>0时系统存在正平衡点E*(H*,P*),其中 正平衡点处的雅可比矩阵为 在系统(4)的线性化系统的平衡点E*(H*,P*)附近加一个时空小扰动,即令 得到微扰线性系统的特征多项式为 |λE-J+Dκ2|=0 其中 可得色散关系: λ2-tr(κ)λ+Δ(κ)=0 (7) 这里 tr(κ)=-(d1+d2)κ2+j11-s (8) Δ(κ)=d1d2κ4+(d1s-d2j11)κ2- (9) 方程(7)的根为: (10) 定理3当ar+hr+m-1>0时, (2)s=s*时,系统在正平衡点E*(H*,P*)周围会出现hopf分支. 时,系统在正平衡点E*(H*,P*)会出现Turing失稳. 这里 (11) 证明: (1)易知s>s*时,tr(κ)<0成立;由于 (12) (2) Hopf分支产生的条件为:Im(Δ(κ))≠0,Re(Δ(κ))=0,κ=0,所以代入(7)、(8)可得Hopf分支参数s的临界值: (3)Turing失稳的条件为Δ(κ)<0且tr(κ)<0. 由(8)可知,当Δ(κ)最小时, 此时 Δ(κ)min= (13) 所以当 有Δ(κ)min<0,又因为s>s*时,tr(κ)<0成立. 证毕. 定理4若系统(4)的正平衡态E*存在,且同时满足条件 (S1):(1-m)(1+c) (S2):2rμ(a+h)2-(h+2-2m+(a+h)2)(T+cH*)≥0 (S3):μ(a+h)2(2h-1+m)-hT(1-m)≥0 则系统的正平衡态E*是全局渐近稳定的. 证明:构造lyapunov函数 (14) E(t)=∬ΩV(H(x,t),P(x,t))dxdy (15) (16) [(H-H*)+(P-P*)]2× (17) 由上 并且 分以下三种情形讨论: 从上面的分析可知,在扩散系数一定的情况下,随着庇护作用的加强,对于系统的稳定性有着促进的作用.在某种程度上适当的加强庇护作用可以使不稳定的正平衡点E*(H*,P*)变得稳定,从而使得濒临灭绝的物种得以持续生存. [1] 王顺庆,王万雄,徐海根.数学生态学稳定性理论与方法[M].北京:科学出版社,2004. [2] 张芷芬,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,1985. [3] 陈兰荪,井竹君.捕食者-食饵相互作用中微分方程的极限环存在性和唯一性[J].科学通报,1984,29(9):521-523. [4] 范 猛,王 克.一类具有HollingII型功能性反应的捕食者-食饵系统全局周期解的存在性[J].数学物理学报,2001(4):492-497. [5] 张 娟,马知恩.一类具有HollingII类功能性反应且存在两个极限环的捕食系统的定性分析[J].生物数学学报,1996,11(4):37-42. [6] 刘启宽,张兆强,陈 冲.一类具有功能反应的食饵-捕食者模型的定性分析[J].重庆理工大学学报(自然科学版),2010,24(1):118-122. [7] S.B.Hsu,T.W.Huang.Global stability for a class of predator-prey systems[J].SIAM Journal on Applied Mathematics,1995,55(3):763-783. [8] A.Gasull,R.E.Kooij,J.Torregrosa.Limit cycle in the Holling-Tanner mode[J].Publicacions Matemtiques,1997,41(1):149-167. [10] T.Saha,C.Chakrabarti.Dynamical analysis of a delayed radio-dependent Holling-Tanner predator-prey model[J].Journal of Mathematical Analysis and Applications,2009,358(2):389-420. [11] Z.Liang,H.pan.Qualitative analysis of a radio-dependent Holling-Tanner predator-prey model[J].Journal of Mathematical Analysis and Applications,2007,334(2):954-964. [12] M.Banerjee,S.Banerjee.Turing instabilities and spatio-temporal chaos in ratio-dependent Holling-Tanner model[J].Mathematical Biosciences,2012,236(1):64-76. [13] 杨晓峰,靳 祯,任变青.具有Smith出生的改进的Holling-Tanner模型的定性分析[J].陕西科技大学学报(自然科学版),2010,28(4):8-11. [14] F.D.Chen,L.J.Chen,X.D.Xie.On a Leslie-Gower predator-prey model in corporating a prey refuge[J].Nonlinesr Analysis,2009,10(5):2 905-2 908. [15] Z.M.Yue,W.J.Wang.Qualitative analysis of a diffusive ratio-dependent Holling-Tanner model with Smith growth[EB/OL].http://dx.doi.org/10.1155/2013/267173,2014-03-01.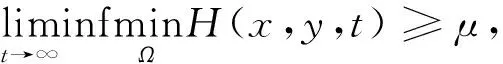
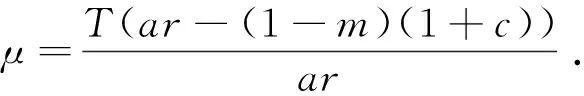
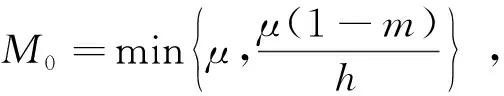
2 平衡点的局部稳定性
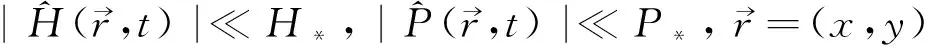
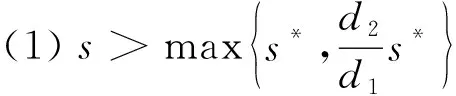
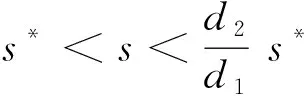
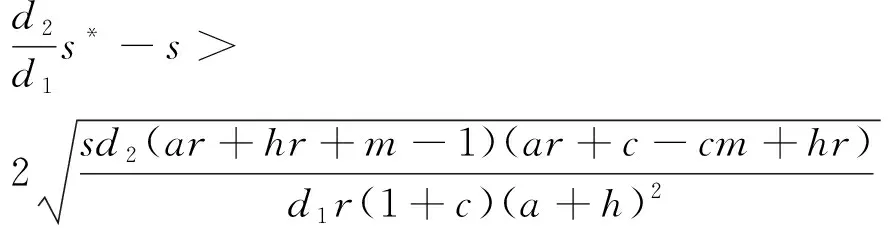
3 正平衡点的全局稳定性
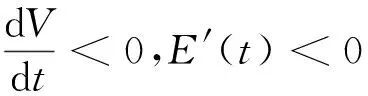
4 庇护效应对系统的影响