一种确定六边形蜂窝芯材共异面弹性模量的简单有限元法

孙德强， 高田莉， 王庆庆， 李文娥，王晨阳， 孙建建， 郑波波

(1.陕西科技大学 设计与艺术学院， 陕西 西安 710021； 2.西安理工大学 印刷包装工程学院， 陕西 西安 710048)

0 引言

六边形蜂窝芯材是一种重要的二维多孔材料，常用六边形蜂窝芯材如图1所示.每一个周期性的特征单元有4个长为l厚为t的倾斜孔壁，2个长为h厚为2t的竖向孔壁.整个蜂窝芯x3方向上的厚度为b.t/l称为壁厚边长比，h/l称为边长比，θ为扩展角.

关于蜂窝芯材共异面弹性模量的求解，近半个多世纪来有很多研究.概括起来主要有能量法、有限元法、实验法和均匀化理论.在能量法方面，Kelsey给出了异面剪切模量G13*和G23*的计算公式[1].基于Kelsey的计算原理Gibson和Ashby导出了各孔壁等厚的蜂窝芯材力学参数的计算公式[2].考虑到商用蜂窝材料双壁厚的影响，Burton和Noor对Gibson公式进行了修正，得出了其力学参数的数学公式，但这些公式没有考虑孔壁伸缩和剪切变形[3].后来富明慧加入了孔壁的伸缩变形，但没有考虑剪切变形的影响，而且他所计算的蜂窝芯是单壁厚的[4].Grediac利用有限元法计算了蜂窝特征单元的异面参数，对Gibson的共面剪切模量公式进行了修正[5].Guo利用二维梁单元法对Gibson的E1*和E2*进行了修正.Chung和Papka[6]在对圆形聚碳酸酯蜂窝材料进行力学响应分析时，采用了基于Timoshenko梁理论的二次梁单元，很好的再现了其静动态响应过程.虽然Timoshenko梁单元适合分析微薄或短粗梁，包含了梁的剪切变形，但是蜂窝铝芯厚度范围变化很大，很多情况下有很大的b/t值，此时就不宜采用梁单元来分析计算，应采用壳单元进行.孙德强等人在利用有限元法分析三角形蜂窝共面动力学行为时就采用了壳单元[7].实验方法上，Nast为等边六边形商用蜂窝纸芯的各项弹性模量设计了实验测试方法；Foo等设计了Nomex纸蜂窝结构的共异面弹性模量的试验测试方法，并对实验样品尺寸的壳模型进行了有限元数值模拟计算，对结果进行了比较，但是计算时采用的模型尺寸大，计算量大[8].在均匀化理论方面，Shi和Tong利用均匀化理论计算了蜂窝材料的性能参数，这种方法考虑了蜂窝的高度和局部线性扭曲的影响，计算精度高[9].

作者曾综合考虑蜂窝孔壁的弯曲、伸缩和剪切变形，推导了其共异面弹性模量的精确计算公式，并设计了基于特征单元的共异面弹性模量的可靠有限元计算方法[10].但这种有限元法要施加复杂的边界条件，构建过程非常复杂.

图1 六边形蜂窝芯材的结构

本文构建了一种基于单元阵列的六边形蜂窝芯材共异面弹性模量的简单有限元计算模型，并利用该模型针对多种尺寸的样品进行了大量的模拟计算.计算结果与已有理论计算结果进行了比较分析，以验证有限元计算模型的可靠性.

1 相关理论

对于如图1所示的双壁厚六边形蜂窝芯材来说，共异面弹性模量E1*、E2*和E3*的Gibson and Ashby公式分别：

(1)

(2)

(3)

其中，Es为壁材的杨氏模量.除了弯曲这一主要变形因素外，共面模量计算公式(1)和(2)没有考虑其余变形因素.综合考虑孔壁的弯曲、拉伸和剪切变形，在Gibson和Ashby共面模量的计算公式基础之上，我们又推导了共面模量E1*和E2*的精确计算公式[10]：

(4)

(5)

其中，vs为孔壁材料的泊松比.

2 有限元建模和计算方法

为了确定六边形蜂窝芯材共面弹性模量，根据ASTM的测试标准[11]，样品的长宽和厚度应分别为220 mm、130 mm和15 mm.根据实验标准GJB 130.1-1986和GJB 130.5-1986，利用压缩试验测试蜂窝芯异面模量时样品的长宽厚应统一为60 mm，单元数量不少于50.我们曾研究并使用基于特征单元的有限元法计算六边形蜂窝芯材共异面弹性模量[10].尽管这样的模型计算效率高，但需要施加复杂的约束以模拟周期性的边界条件.因此，这样的模型很难再现样品实际承受的载荷条件.

图2 有限元几何模型尺寸参数

为了克服这一缺陷，在此建立了基于单元阵列的有限元计算模型，求解E1*、E2*和E3*所用样品沿x3方向的视图分别如图2(a)～(c)所示，特征单元的尺寸图如图2(d)所示.该模型是用ANSYS/Multiphysics

建立并求解.合理控制单元数量使样品的外形尺寸刚好稍大于试验样品的标准尺寸.使用线弹性壳Shell99进行网格划分.竖向孔壁上壳的厚度是斜向孔壁上壳厚度的两倍.在计算共面模量时，一端所有节点固定，在另一端的所有节点上施加拉伸位移载荷.共面弹性模量E1*和E2*的位移载荷分别为ΔL1和ΔL2.在求解E3*的模型中，底面所有线上节点都固定，在上表面所有线上施加位移载荷ΔL3.壁材是各向同性线弹性的，杨氏模量、泊松比和密度分别设为68.97 GPa、0.35和2 700 kg/m3.

三种有限元受力分析计算后可得到固定节点的合力分别为∑F1,∑F2和∑F3.图2(a)中用来求解E1*的样品在x1和x2方向上样品的单元数量分别为m1和n1.则L1=2m1lcosθ+(2m1-1)t，W1=n1(lsinθ+h)+lsinθ.图2(b)中用来求解E2*的样品在x2和x1方向上样品的单元数量分别为m2和n2.则L2=m2(lsinθ+h)+lsinθ，W2=(2n2+1)lcosθ+2n2t. 图2(c)中用来求解E3*的样品在x2和x1方向上样品的单元数量分别为m3和n3.则L3=m2(lsinθ+h)，W3=2n3lcosθ+(2n3-1)t.最终，三个模量的计算公式分别为：

E1*=L1×∑F1/(W1b×ΔL1)

(6)

E2*=L2×∑F2/(W2b×ΔL2)

(7)

E3*=b×∑F3/(L3W3×ΔL3)

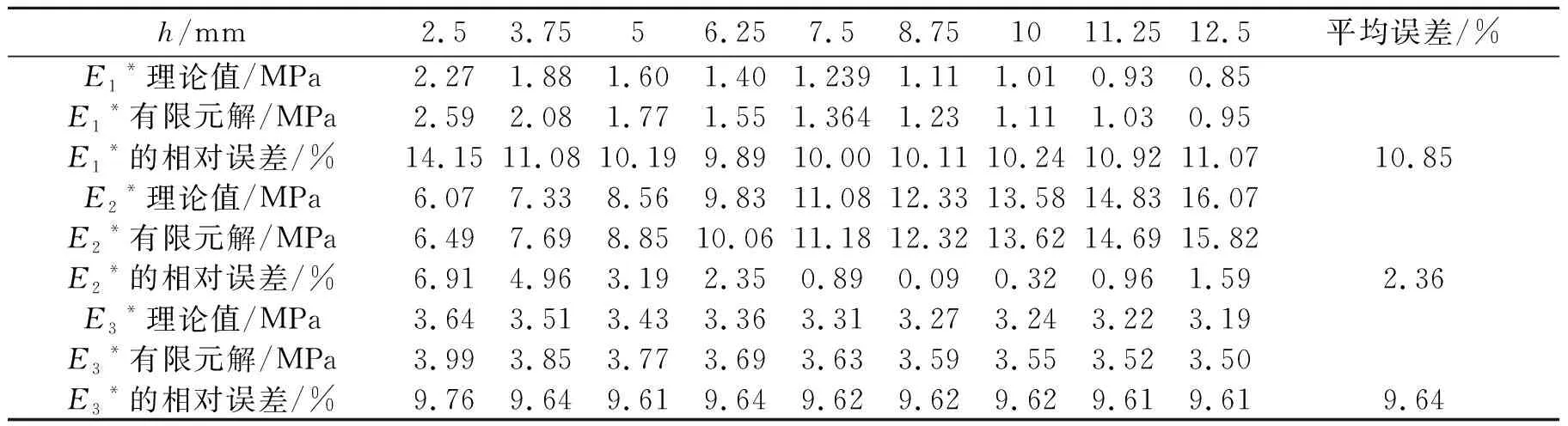
(8) 表1 h/l变化时E1*,E2*,E3*的值及其误差

表2 θ变化时E1*,E2*,E3*的值及其误差

表3 t变化时E1*,E2*,E3*的值及其误差

3 验证与分析

为了验证有限元计算模型的可靠性，固定l=5 mm，h/l=0.5～2.5，θ=10～80 °，t=0.05～0.3 mm.保持h/l、θ和t其中之一变化，其余参数固定的情况下，进行相应共异面弹性模量的计算，以研究这一变化的参数对所有弹性模量的影响.

保持θ=45 °和t=0.15 mm，h/l变化的9组样品进行模拟计算，计算得到的E1*、E2*和E3*列于表1.保持t=0.15 mm和h/l=1.5，θ变化的8组样品进行模拟计算，计算得到的E1*、E2*和E3*列于表2.保持h/l=1.5和θ=45 °，t变化的11组样品进行模拟计算，计算得到的E1*、E2*和E3*列于表3.

由表1～3中的数据可以看出，有限元计算的弹性模量要比相应理论值略大，但对于所有样品相对误差最大不超过11%.在误差允许的范围内，可认为有限元解与理论解相吻合，印证了前述有限元模型的可靠性.

4 结论

对现有六边形蜂窝芯材弹性模量计算方法的研究表明，很有必要来构建基于单元阵列的相应有限元计算方法.本文构建了相关有限元模型，并介绍了相关计算原理.该模型参考相关试验标准进行，载荷条件施加简单方便.利用该模型，对具有各种结构参数的样品进行了大量模拟计算.将理论计算结果和有限元计算结果进行对比分析，发现两者吻合较好，证明了本有限元模拟方法的可靠性.

[1] Kelsey S,Gellatly R,Clark B.The shear modulus of foil honeycomb cores[J].Aircr. Eng.,1958(30):294-302.

[2] Gibson L J,Ashby M F.Cellular solids:structures and properties,2nd ed.[M].Cambridge:Cambridge University Press,1997.

[3] Burton W,Noor A.Assessment of continuum models for sandwich panel honeycomb cores[J].Comput.Methods Appl.Mech.Eng.,1997,145(3-4):341-360.

[4] 富明慧,尹久仁.蜂窝芯层的等效弹性参数[J].力学学报,1999,31(1):113-118.

[5] Guo X,Gibson L.Behavior of intact and damaged honeycombs:A finite-element study[J].Int.J.Mech.Sci.,1999,41(11):85-105.

[6] Scott D Papka,Stelios Kyriakides.In-plane crushing of a polycarbonate honeycomb[J].International Journal of Solids and Structures,1998,35(3):239-267.

[7] 孙德强,宫 凯,李国志,等.三角形蜂窝的共面冲击动力学[J].陕西科技大学学报,2013,31(1):98-105.

[8] Choon Chiang Foo,Gin Boay Chai,Leong Keey Seah.Mechanical properties of Nomex material and Nomex honeycomb structure[J].Composite Structures,2006,19(3):177-183.

[9] Shi G,Tong P.Equivalent transverse shear stiffness of honeycomb cores[J].Int.J.Solids Struct.,1995,32(10):1 383-1 393.

[10] 孙德强,张卫红,孙玉瑾.蜂窝铝芯的弹性模量和材料效率分析[J].力学与实践,2008,30(1):35-40.

[11] ASTM Section 15-1998,General products,chemical specialities and end use products[S].