卫星定位定轨系统SPODS:理论与测试
2014-06-27魏子卿阮仁桂贾小林吴显兵宋小勇冯来平朱永兴
魏子卿,阮仁桂,贾小林,吴显兵,宋小勇,毛 悦,冯来平,朱永兴
1.西安测绘研究所,陕西西安 710054;2.地理信息工程国家重点实验室,陕西西安 710054
卫星定位定轨系统SPODS:理论与测试
魏子卿1,2,阮仁桂1,2,贾小林1,2,吴显兵1,2,宋小勇1,2,毛 悦1,2,冯来平1,2,朱永兴1,2
1.西安测绘研究所,陕西西安 710054;2.地理信息工程国家重点实验室,陕西西安 710054
卫星定位定轨系统SPODS是西安测绘研究所开发的GNSS定位定轨软件。该软件目前能够处理GPS数据,具有高精度GPS定位定轨能力。本文简要介绍SPODS的基本理论和性能测试情况。性能测试使用了2009年1月4日至10日大约127个lGS站采集的GPS数据。结果表明,GPS卫星轨道解与lGS最终轨道的1D RMS差为1.1 cm;站坐标日解的重复性,水平分量为1.5 mm,高度分量为4.5 mm;极坐标和日长变化解与lGS最终产品的一致性,分别为0.025 mas、0.093 mas和0.013 ms/d。
GNSS;精密定位;精密定轨;ERP确定;卫星定位定轨系统
1 引 言
全球导航卫星系统(GNSS)是当今最重要的空间大地测量技术之一。导航定位和授时是GNSS的基本功能。正是由于它的精密定位功能,GNSS给大地测量带来了革命性变化,给地学的其他领域也带来了新的活力。当然,精密定位必须有精密轨道支撑,也必须有相应的软件手段。开发精密定位定轨软件,一直都受到学者们的高度重视。目前国内外已涌现诸多优秀软件,如麻省理工学院(MIT)和Scripps海洋研究所(SIO)联合研制的GAMIT/GLOBK,伯尔尼大学研制的BERNESE,喷气推进实验室(JPL)研制的GIPSY-OASIS,武汉大学研制的PANDA等。这些软件已用于IGS轨道产品的生成,有些软件还在地学界广泛应用。认识到精密定位定轨的重要性,以及自主开发相关软件的必要性,西安测绘研究所近年一直致力于GNSS定位定轨软件的研制,特别是第二作者以主要精力投入程序的编写,目前已研制成功首版卫星定位定轨系统(satellite positioning and orbit determination system,SPODS)。本文将简要介绍SPODS的基本理论及其性能测试情况,以此作为该项努力的阶段性小结。
2 理 论
SPODS的软件结构和数据流程如图1所示。
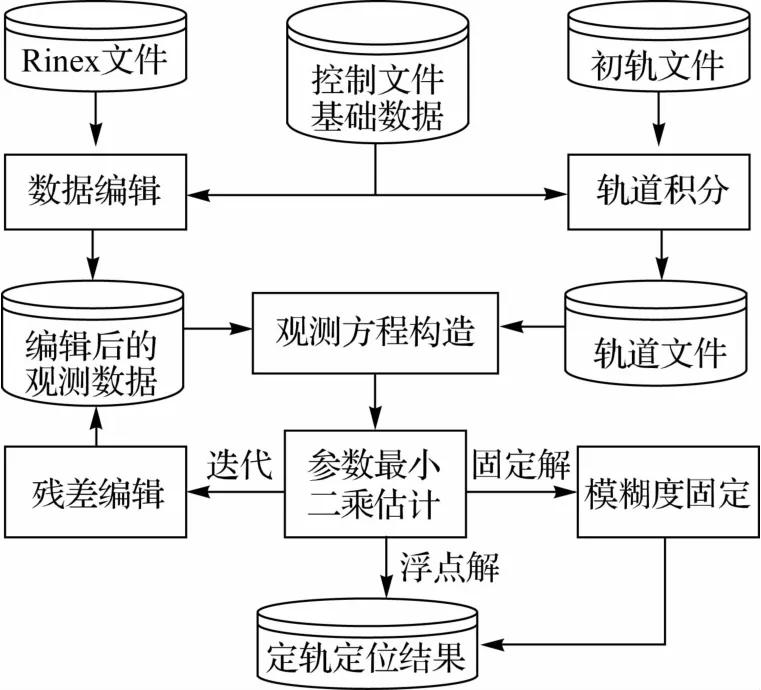
图1 软件结构及数据流程Fig.1 Software structure and data flow
SPODS采用双频消电离层组合的非差相位和伪距作为观测量。采用TurboEdit法[1]进行相位周跳检测和修复。不可修复的周跳加以标记,在后续的参数估计过程加入模糊度参数。通过验后残差分析,进一步探测周跳和粗差。如此迭代,直至未发现新的周跳和粗差为止。
固定模糊度在双差相位上实现[2-5]。参考文献[4]方法,首先依次在星座级和全网级选取独立双差模糊度,然后依据累积概率(阈值设为≥99%),序贯地将模糊度固定于最近的整数。用伪距和相位的MW组合[2],先固定宽巷模糊度,后固定窄巷模糊度。实际表明,固定模糊度会使站坐标和轨道参数的解算精度提高1~2倍[2]。
卫星轨道用初始状态向量和一组动力学模型参数描述[6]。卫星位置、状态转移矩阵和敏感矩阵在等间隔点上的值,利用Adams-Bashforth-Moulton预报校正积分器,通过数值积分得到。它们在任意时刻的值,利用拉格朗日多项式插值得到。考虑的摄动力包括:地球非球形引力、日月与行星摄动、太阳光压及相对论效应。地球引力采用12阶EGM96模型,考虑了固体潮和极潮引起的引力位变化[7],引力加速度表示为卫星坐标x、y、z的函数形式[6,8]。日月与行星历表采用JPL DE405。太阳光压采用ECOM模型,用D、Y、B方向的常数和周期摄动加速度表示[9]。
轨道计算在地心天球参考系GCRS进行,卫星轨道产品和站坐标参考于国际地球参考系ITRS。GCRS与ITRS之间的关系用以地球定向参数为函数的旋转矩阵表示,它们之间的转换按照IERS Conventions(2003)[7]进行,岁差-章动模型采用IAU2000A[7]。EOP参数初值采用IERS A公报值,极坐标和UT1顾及了由海潮引起的周日和半周日变化,极坐标还考虑了相应于周期小于2 d的空间运动的天平动改正[7]。
观测量的改正项包括:卫星和接收机天线相位中心偏差和变化、卫星相对论钟差、对流层延迟、电离层延迟、潮汐(固体潮、极潮和海潮负荷)位移改正。相位数据还考虑了Wind-up效应[10]改正。卫星和接收机天线相位中心偏差和变化数据取自IGS ANTEX文件,相位中心改正顾及了卫星姿态影响[11]。对流层延迟改正使用标准大气,采用Saastamoinen天顶延迟模型和Beohm&Neill的映射函数[12]。潮汐位移改正执行IERS Conventions(2003)[7]。
估计参数划分为全局参数和局部参数。前者包括静态测站坐标、卫星轨道参数(初始状态参数和力模型参数)、ERP参数、对流层参数(湿天顶延迟和延迟水平梯度)和模糊度参数等。后者包括动态测站(如果有的话)坐标参数和卫星与接收机钟差参数(用白噪声模型化)。参数估计采用最小二乘法。逐历元构建观测方程,组成法方程,并进行局部参数约化,将约化法方程累加到总(约化)法方程。全局参数通过总约化法方程矩阵的Cholesky分解求逆[13]得到。然后将全局参数逐历元后向回代得到局部参数,并计算验后残差。程序算法充分利用设计矩阵的稀疏特性,以求节约内存和提高计算效率。
SPODS用FORTRAN 90/95编写,约25 000行代码。
3 测 试
SPODS的测试使用了2009年1月4日至10日大约127个IGS站的GPS数据,采样间隔为30 s。127个站的分布如图2所示。
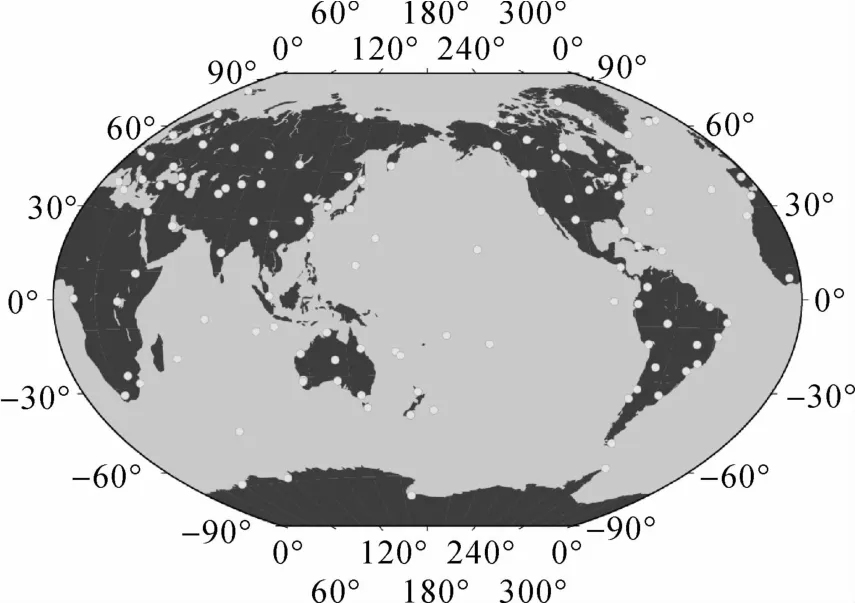
图2 测试用的IGS站分布图Fig.2 Distribution of IGS stations used in the test
SPODS的测试条件:
(1)非差消电离层伪距和相位的先验误差分别取2.0 m和2 cm,按照1/sin2E(E为高度角)赋权,高度截止角取10°。
(2)站坐标初值取自IGS05.SNX文件,其中10个站的每一坐标分量的先验误差取2 cm,其余站取1 km。
(3)卫星轨道参数包括6个初始状态参数和5个光压模型参数(D0、Y 0、B0、Bc和Bs)[9],它们的初值通过广播星历拟合得到。
(4)EOP先验值取自IERS A公报。估计参数包括:极坐标xp、yp及其变率xp、yp,以及日长变化δlod/lod。
(5)每2 h估计1个湿分量天顶延迟参数,每天估计1组对流层延迟水平梯度参数。
SPODS的测试结果:
下面给出SPODS的卫星轨道、站坐标和ERP参数解。值得说明,通过比较SPODS轨道和ERP解与IGS综合产品的不符值,评估前者的精度(accuracy);通过比较SPODS站坐标单日解的重复性,评估其精密度(precision)。
3.1 GPS轨道
将卫星轨道的SPODS单日解与当周的IGS最终轨道比较,得到两种轨道的径向(R)、迹向(T)、法向(N)及三维(3D)位置的RMS差值。图3按天号绘出所有卫星的平均RMS差。图3显示,径向RMS差不超过1 cm,迹向和法向不超过1.5 cm,3D位置不超过2.5 cm。关于7 d的平均RMS差,3个方向依次为0.9 cm,1.1 cm和1.2 cm。
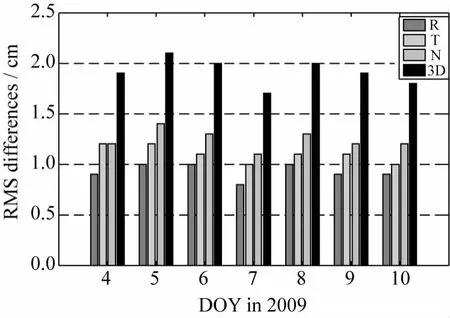
图3 SPODS轨道与IGS最终轨道之差的RMS值Fig.3 RMS differences between SPODS orbits and final IGS orbits
类似的,比较9个IGS分析中心的最终轨道与IGS最终轨道,得到前者与后者的1D位置差的RMS值。图4是10个轨道与IGS最终轨道的RMS 1D差之序列图,其中XRI标示SPODS轨道。由图看出,相对9个IGS分析中心的轨道,SPODS轨道处于相当不错的地位。
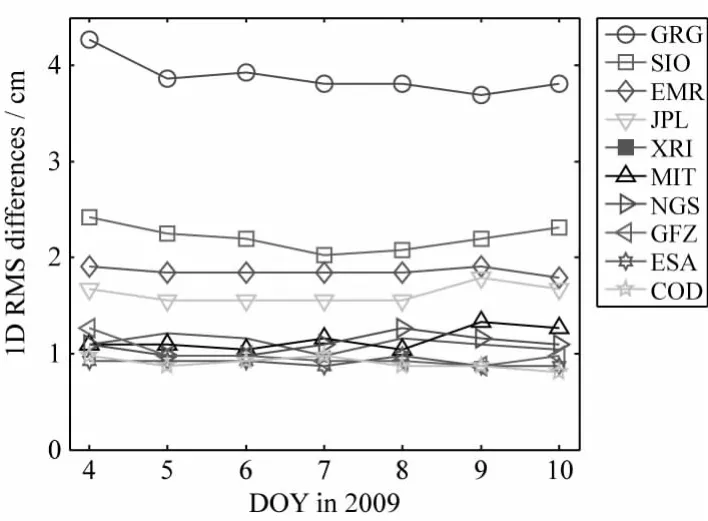
图4 SPODS/IGS分析中心最终轨道与IGS最终轨道之差的RMS 1D值Fig.4 RMS 1D differences between SPODS/IGS analysis centre orbits and final IGS orbits
3.2 站坐标
图5绘出每天均有数据的99个站的北(N)、东(E)和上(U)分量坐标的平均日重复性。可以看出,N/E分量的重复性在5 mm以内,U分量小于10 mm(两站除外)。关于7 d的平均日重复性,3个分量分别为1.5 mm、1.5 mm和4.2 mm。
3.3 ERP参数
表1列出SPODS的ERP日解与IGS综合产品的差值。可以看出,其差值对于xp、yp和δlod/lod分别不超过0.05 mas、0.12 mas和0.03 ms/d。关于7 d的RMS差,它们分别为0.025 mas、0.093 mas和0.013 ms/d。
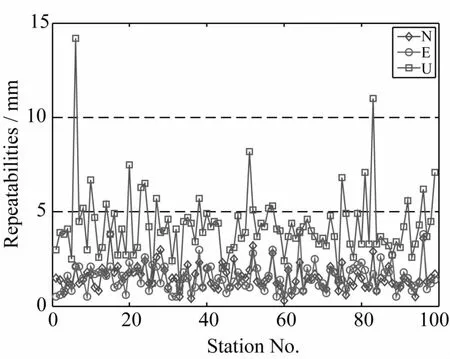
图5 SPODS站坐标解的重复性Fig.5 Repeatabilities of SPODS daily solutions of station coordinates

表1 SPODS ERP解与IGS ERP最终值的差值Tab.1 Differences between SPODS ERP solutions and final IGS ERP values
4 结 论
西安测绘研究所近年一直致力于GNSS定位定轨软件的研制,目前已取得初步成果,研制成功卫星定位定轨系统SPODS第一版。利用2009年1月4日至10日大约127个IGS站的GPS数据进行的性能测试结果表明,站位置水平分量的日重复性为1.5 mm,垂直分量日重复性为4.5 mm;GPS卫星轨道与IGS最终轨道的1D差为1.1 cm。极坐标和日长变化解与IGS最终综合值分别符合至0.025 mas、.093 mas和0.013 ms/d。数据显示,目前SPODS解已具有相当好的精度水平。
下一步任务是,改进SPODS的性能,增强其功能,近期拟增加处理北斗数据的能力。
致谢:感谢德国地学研究中心(GFZ)的葛茂荣博士,同他的讨论和交流使笔者获益颇多,特别是他对光压模型参数的意见,对软件研制起到很大作用。
[1] BLEWITT G.An Automatic Editing Algorithm for GPS Data[J].Geophysical Research Letter,1990,17(3):199-202.
[2] BLEWITT G.Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km[J].Journal of Geophysical Research,1989,94(B8):10,187-110,203.
[3] DONG D N,BOCK Y.Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J].Journal of Geophysical Research,1989,94(B4):3949-3966.
[4] GE M,GENDT G,DICK G,et al.Improving Carrier-Phase Ambiguity Resolution in Global GPS Network Solutions[J].Journal of Geodesy,2005,79(1-3):103-110.
[5] MERVART L.Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System[D].Berne:University of Berne,1995.
[6] MONTENBRUCK O,GILL E.Saltellite Orbits Models,Methods,and Applications[M].Berlin:Springer-Verlag,2001.
[7] MCCARTHY D D,PETIT G E.IERSConventions(2003)[R].Frankfurt am Main:Verlag des Bundesamtes für Kartographie und Geod¨asie,2004.
[8] CUNNINGHAM L E.On the Computation of the Spherical Harmonic Terms Needed during the Numerical Integration of the Orbital Motion of an Artifical Salellite[J].Celestial Mechanics,1970(3):207-216.
[9] SPRINGER T A.Modeling and Validating Orbits and Clocks Using the Global Positioning System[D].Berne:Astronomical Institute,University of Berne,1999.
[10] WU J T,WU S C,HAJJ G A,et al.Effects of Antenna Orientation on GPS Carrier Phase[J].Manuscripta Geodaetic,1993,(18):91-98.
[11] BAR-SEVER Y E.A New Model for Yaw Attitude of Global Positioning System Satellites[J].Journal of Geodesy,1997,70:714-723.
[12] BOEHM J,NEILL A,TREGONING P,et al.Global
Mapping Function(GMF):A New Empirical Mapping Function Based on Numerical Weather Model Data[J/OA].Geophysical Research Letters,2006,33(L07304).[13] BIERMAN G J.Factorization Methods for Discrete Sequential Estimation[M].New York:Academic Press,1977:241.
(责任编辑:张燕燕)
Satellite Positioning and Orbit Determination System SPODS:Theory and Test
WEl Ziqing1,2,RUAN Rengui1,2,JlA Xiaolin1,2,WU Xianbing1,2,SONG Xiaoyong1,2,MAO Yue1,2,FENG Laiping1,2,ZHU Yongxing1,2
1.Xi’an Research lnstitute of Surveying and Mapping,Xi’an 710054,China;2.State Key Laboratory of Geo-information Engineering,Xi’an 710054,China
The Satellite Positioning and Orbit Determination System(SPODS)is a software package for GNSS positioning/orbit determination,developed by the Xi’an Research lnstitute of Surveying and Mapping.So far it has been able to treat GPS data and has the capability of high precision GPS positioning and orbit determination.The underlying theory and the performance test are briefly addressed.The test utilizes the GPS data collected from some 127 lGS stations during days 4~10 of 2009.The results show that the rms 1D difference is 1.1 cm between SPODS orbits and final lGS combined orbits,and that the repeatability of daily solutions of station coordinates is 1.5 mm for horizontal components,and 4.5 mm for height component,and that the consistency of ERP solutions with final lGS values is 0.025 mas,0.093 mas and 0.013 ms/d respectively for pole coordinates and changes in length of day.
GNSS;precise positioning;precise orbit determination;ERP determination;SPODS
P228
A
1001-1595(2014)01-0001-04
2013-09-23
魏子卿(1937—),男,中国工程院院士,近期研究方向为大地坐标系、大地边值问题及GNSS测量。First author:WEl Ziqing(1937—),male,academician of Chinese Academy of Engineering,majors in geodetic coordinate system,geodetic boundary value problem and GNSS.
WEI Ziqing,RUAN Rengui,JIA Xiaolin,et al.Satellite Positioning and Orbit Determination System SPODS:Theory and Test[J].Acta Geodaetica et Cartographica Sinica,2014,43(1):1-4.(魏子卿,阮仁桂,贾小林,等.卫星定位定轨系统SPODS:理论与测试[J].测绘学报,2014,43(1):1-4.)
10.13485/j.cnki.11-2089.2014.0001
修回日期:2013-10-10
