含二次矩及记忆强度的做市商资产定价模型

坚红玲

(新疆大学数学与系统科学学院，乌鲁木齐 830046)

含二次矩及记忆强度的做市商资产定价模型

坚红玲

(新疆大学数学与系统科学学院，乌鲁木齐 830046)

讨论了在做市商机制下，当图表分析者的条件期望及方差均是加权移动平均过程时的基于基本面分析者及图表分析者的行为资产定价模型。同时在市场分数中引入了记忆强度，通过稳定性和分支分析，讨论了记忆强度、加权过程及时变二次矩过程对模型稳定性和分支的影响。

异质性念;二次矩;记忆强度;稳定性

以有效市场假说为前提，以现代资产组合金融理论为基石建立起来的传统资产定价理论已具有完备的理论框架，但实证研究表明该理论还有不符合实际情况的地方。行为金融学通过引入投资者在价格预期方面存在的意见分歧来构建基于投资者异质信念的均衡资产定价模型，解释了大量金融理论所无法解释的金融异象，同时也表明了在投资者异质信念下资产定价研究的重要性。

大量资产价格模型是建立在代表性交易者及理性预期的极度信息假设之上。金融资产价格动力学是将交易者的异质性与有限理性相结合。早期MarkB.Garman［1］，Day和Huang［2］等引入了有限理性，随后Brock和Hommes［3－4］引入自适应理性均衡的概念。有限理性的交易者能够根据过去行为结果选择不同的交易策略，这种动态系统能产生复杂动力学行为。Chiarella和He［5－7］对文献［4］的模型进行了扩展，在瓦尔拉斯拍卖人机制和做市商机制下考虑时变(同质)方差、异质风险、学习过程的情况，研究了相对风险态度、不同的学习机制、不同的市场出清机制对资产价格动力学的影响。Gaunerdorfer［8－9］在适应性函数中引入了稳定性因素，考虑了时变方差、技术交易规则仅与最近观察价格有关，在市场分数中加入了补偿函数，两者都能阻止价格产生投机泡沫。Roberto Dieci［10］讨论了极限几何衰减过程下市场分数为固定和时变时的价格动力学。Carl［11］引入了不同于文献［10］的另一学习过程，同时表明这种二次矩能改变非线性动力学的结果。MiroslavVerbi cˇ［12］在市场分数中引入了记忆强度。

金融市场模型中确定资产价格时使用最多的是瓦尔拉斯拍卖人机制和做市商机制。相对瓦尔拉斯均衡拍卖人机制来说，做市商机制能对市场做更为贴近的分析。很多文献考虑的是一次矩(价格或收益的)异质期望而不是二次矩，而二次矩(条件方差)估计比一次矩(条件期望)更容易。因此，交易者更加倾向于方差估计。

本文在文献［11］的基础上考虑了做市商机制下的资产价格模型，结合文献［12］对记忆强度的讨论，建立了做市商机制下含二次矩及记忆强度的资产价格模型，利用差分理论及分支理论讨论了主要参数对平衡点的稳定性及分支的影响。

1 含二次矩及记忆强度的资产定价模型

考虑金融市场中存在一种风险资产和一种无风险资产的情况。总收益为R=1+r，r为每个交易阶段的无风险收益率，pt表示t时期的风险资产价格，yt为t时期的股息，¯y是股息过程的期望，则t+1时期h类交易者的财富为

其中Rt+1=pt+1+yt+1－Rpt为超额收益。假设h类交易者有CARA效用函数uh(W)=－exp［－ahW］，ah为风险厌恶系数，则最大化期望效用财富的最优需求为

其中:Eh，t，Vh，t分别表示基于t时期信息集Ft= {pt，pt－1，…;yt，yt－1，…}时h类交易者的条件期望及条件方差;p*=¯y/(R－1)是常基准价格。

在下面的讨论中，将所有的交易者分为基本面分析者和图表分析者。

基本面分析者的条件期望及方差为:

2 确定性动力系统的讨论

对于式(11)，令随机项为0，xt+1=pt+1－p*，得到相应的6维确定性动力系统，并令yt+1=xt，则系统可表示为下列形式:

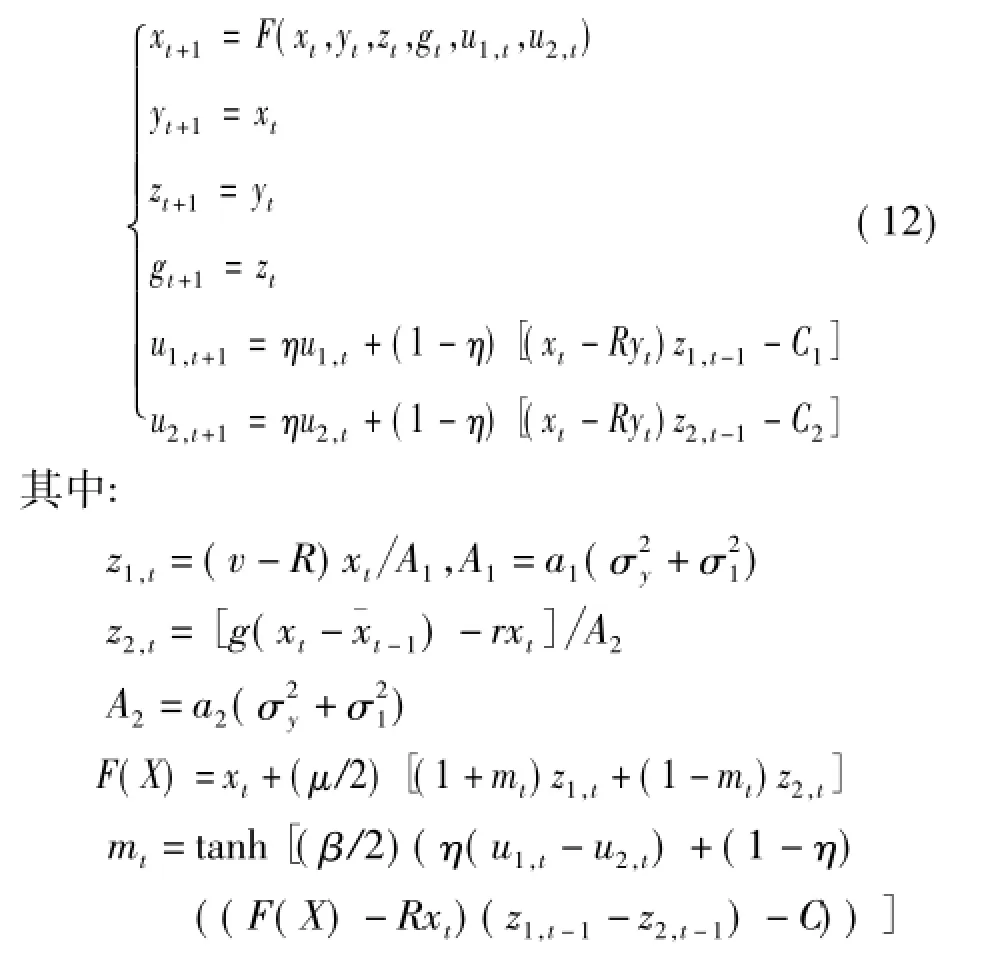
3.1 基本面分析者与追风者

现在来讨论g＞0时平衡点的存在性及局部渐近稳定性。

定理1对于6维确定性系统(12)，存在唯一的平衡点X*=(0，0，0，0，－C，0)，相应的基准价格pt+1=p*。

定理2假设g＞0，对于确定性系统(12)，有以下几种情况:

情况1当［R(x0+a)－a］x0＜1+4A1/ μ(1+m0)时，p*是局部渐进稳定的(LAS)，当且仅当w∈［0，1)时，v＜v3(g)=c1/g－c2－c3g;w= 1时，g＜g'=2A1［μ(1+m0)］。当v=v3(g)时存在一对共轭特征根λ=exp［±iθ］，产生Hopf分支。

情况2当4A1［μ(1+m0)］＜［R(x0+a)－a］/x0＜1+4A1/μ(1+m0)时，存在w∈［0，1)，使

①w＜w1时，存在g*＞0使p*是LAS，当且仅当g＜g*，v＞v2(g);g＞v－13(1)，v＜v3(g)，v2(g)=［R(x0+a)－a］x0－4A1μ(1+m0)－(2aw x0)g;

②w1≤w＜1时，p*是LAS，当且仅当g＜v－12(0)，v＞v2(g)，g＞v－13(1)，v＜v3(g);

③w=1，p*是LAS，当且仅当g＜v－12(0)，v＞v2(g)，g＜g3，当v=v2(g)时存在特征值λ=－1，产生Flip分支，v=v3(g)时产生Hopf分支。

情况3当［R(x0+a)－a］x0≥1+4A1/μ(1+m0)时，存在g*＞0，w1、w2满足0＜w1＜w2＜1时:

①w＜w1时，不存在稳定区域;

②w1≤w≤w1时，p*是LAS，当且仅当g＜g*，v＞v2(g);g＞v3－1(1)，v＜v3(g);

③w2≤w＜1时，p*是LAS，当且仅当g＜(0)，v＞v2(g);g＞(1)，v＜v3(g);

当g＞0时，由π1＞0恒成立，4个条件减少为π2＞0，π3＞0，π4＞0。因此平衡点的局部稳定区域边界取决于(g，v)参数图中π2=π3=π4=0的相对位置。由π2=π3=π4=0可得下列方程:

当［R(x0+a)－a］x0＜1+4A1［μ(1+m0)］时，平衡点在(g，v)平面上的稳定区域及分支边界如图1所示。由定理2知:随着w的增加，平衡点的稳定区域不断增加。分支边界与均值回馈速率、外推速率及加权平均过程的权重有极大相关性。在经济意义下，基本面分析者具有稳定市场的作用，图表分析者具有不稳定市场的作用。然而，当基本面分析者反应过激时也能使市场价格不稳定，在一定情况下，图表分析者反应不足也能使市场趋于稳定。

图1 g＞0时情况1的稳定区域及分支边界

3.2 基本面分析者与逆风者

由定理3知:平衡点在(g，v)平面上的稳定区域及分支边界有3种不同情况，分别如图2～4所示。当外推速率较小(较大)时，逆风者具有稳定(不稳定)作用。基准价格的稳定性取决于两类交易者活动的均衡程度。注意到随着g的增加，v2(g)，v3(g)均减少。这意味着当基本面分析者反应过激(v较大)时，逆风者外推速率的稳定区域在不断增加;当最近一时期的权重w较大(即过去的价格权重1－w较小)时，逆风者对市场价格反应不足，导致市场价格周期性波动;当最近一时期的权重w较小(即过去的价格权重1－w较大)时，基本面分析者有稳定市场的作用，故市场价格在基准价格附近上下波动。

图2 w∈［w2，1］时平衡点的稳定区域及分支边界

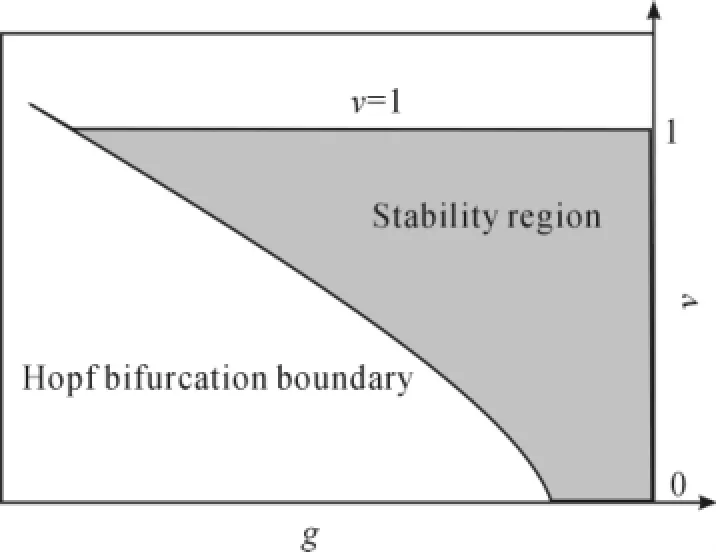
图3 w∈［0，w1］时平衡点的稳定区域及分支边界

图4 w∈(w1，w2)时平衡点的稳定区域及分支边界

3 结束语

本文建立了含二次矩及记忆强度的做市商资产价格模型。在该模型基础上讨论了图表分析者为追风者及逆风者时的平衡点的稳定区域及主要参数对模型的影响。结果显示:模型存在唯一的基本平衡点;记忆强度的引入不改变模型的平衡点及稳定区域;无论图表分析者是追风者还是逆风者，都不会产生Pitchfork分支;二次矩的引入能更好地模拟资本市场。

［1］Garman M.Market microstructure［J］.Journal of Financial Economics，1976(3):257－275.

［2］Day，Huang，Bulls.bears and market sheep［J］.Journal of Economic Behavior and Organization，1990，14:299－329.

［3］Brock W，Hommes C.A rational route to randomness［J］.Econometrica，1997，65:1059.

［4］Brock W，Hommes C.Heterogeneous beliefs and routes to chaos in a simple asset pricing model［J］.J Econom Dyn Control，1998，22:1235.

［5］Chiarella C，He X.Asset pricing and wealth dynamics under heterogeneous expectations［J］.Quantitat Finan， 2001(1):509.

［6］Chiarella C，He X.Heterogeneous beliefs，risk and learning in a simple asset pricing model［J］.Comput Econom，2002，19:95－132.

［7］Chiarella C，He X.Heterogeneous beliefs，risk and learning in a simple asset pricing model with a market maker［J］.Macroeconom Dyn，2003(7):503.

［8］Gaunersdorfer A.Endogenous fluctuations in a simple asset pricing model with heterogeneous agents［J］.J Econom Dyn Control，2000，24:799－831.

［9］Gaunersdorfer A，Hommes C，Wagener F.Bifurcation routes to volatility clustering under evolutionary learning［J］.Journal of Economic Behaviour$＆$Organization，2008，67:27－47.

［10］Dieci R，Foroni I，Gardini L，et al.Market mood，adaptive beliefs and asset price dynamics［J］.Chaos Solitons and Fractals，2006，29:520－534.

［11］Carl Chiarella，He X Z，Duo Wang.A behavioral asset pricing model with a time－varying second moment.Chaos［J］.Solitons and Fractals，2006，29:535－555.

［12］Miraslov Verbi c.On the role of memory in an asset pricing model with heterogeneous beliefs［J］.Financial Theory and Practice，2008，32(2):195－229.

［13］王联，王暮秋.常差分方程［M］.乌鲁木齐:新疆大学出版社，1991:202－204.

(责任编辑 刘舸)

Asset Pricing Model with Second Moment and Memory Intensity under Market Maker

JIAN Hong－ling
(College of Mathematics and Systems Science，Xinjiang University，Urumqi 830046，China)

We develop a simple behavioral asset pricing model with fundamentalists and chartists in order to study price behavior under the market maker scenario when chartists estimate both conditional mean and variance by using a weighted averaging process and introduce the fractions with memory intensity.Trough a stability and bifurcation analysis，the model impact of memory intensity，the weighting process and time－varying second moment are examined.

heterogeneous expectations;second moment;memory intensity;stability

O211.9

A

1674－8425(2014)04－0143－07

10.3969/j.issn.1674－8425(z).2014.04.030

2013－10－11

坚红玲(1989—)，女，甘肃人，硕士研究生，主要从事数理金融研究。

坚红玲.含二次矩及记忆强度的做市商资产定价模型［J］.重庆理工大学学报:自然科学版，2014(4):143－149.

format:JIAN Hong－ling.Asset Pricing Model with Second Moment and Memory Intensity under Market Maker［J］.Journal of Chongqing University of Technology:Natural Science，2014(4):143－149.