实矩阵的正交相似标准形

呙林兵,陈忠 (长江大学一年级教学工作部,湖北荆州 434025)

实矩阵的正交相似标准形

呙林兵,陈忠 (长江大学一年级教学工作部,湖北荆州 434025)

通过对实数域上矩阵当特征值全为实数、全为虚数和既有实数又有虚数的情形下矩阵的正交相似标准形研究,得到了任意实矩阵正交相似标准形的具体形式,对矩阵的标准形的内容进行了补充。

矩阵;正交矩阵;特征值;标准形

矩阵标准形有多种形式,在很多文献中对实矩阵的等价标准形、相似标准形、合同标准形以及实对称矩阵的正交相似标准形进行研究[1-2],但对一个任意实矩阵,具有怎样的正交相似标准形,没有进行讨论。下面就实矩阵的特征值全为实数、全为虚数和既有实数又有虚数的情形下,对矩阵的正交相似标准形进行了研究。

1 基本概念

2 主要定理

定理1 设A为n阶实方阵,且A的特征值λ1,λ2,…,λn都是实数,则必存在正交矩阵Q,使得QTAQ为上三角矩阵,且对角线上的元素为λ1,λ2,…,λn。

又因相似矩阵有相同的特征值[3],则A1的特征值必为λ2,λ3,…,λn,对A1用数学归纳法,则存在n-1阶正交矩阵Q1,使得:

由引理1知H1为正交矩阵,从而Q也为正交矩阵。

推论1[3]任意的实对称矩阵A必存在正交矩阵Q,使得:

QTAQ=diag(λ1,λ2,…,λn) (λ1,λ2,…,λn为A的特征值)定理2 设A是2s阶实方阵,A的特征值为λi=ai±i bi,这里ai、bi均为实数,且bi≠0,i= 1,2,…,s,则必存在正交矩阵Q,使得:

定理3 设A是n阶实方阵,λ1,λ2,…,λr是矩阵A的实特征值,λi=ai±i bi是A的复特征值, ai、bi均为实数,且bi≠0,i=1,2,…,s,r+2s=n,则必存在正交矩阵Q,使得:

其中,Ai都是2阶实矩阵,Ai的特征值为λi=ai±i bi,i=1,2,…,s。

证明 因为A为实方阵,λ1,λ2,…,λr是实数,由定理1及定理1的证明可知,存在有限个实镜象矩阵H1,H2,…,Hl,l≤r,使得:

由定理3显然可得如下的定理4。

定理4 设A是n阶实方阵,则必存在正交矩阵Q,使得:

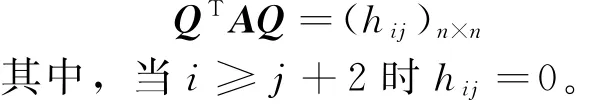
[1]孔莉芳,廖大庆,刘金波.实域中矩阵的几种标准形式及应[J].大学数学,2007,23(6):158-162.

[2]高遵海,叶正道.关于实数域上矩阵的相似标准形[J].武汉工业学院学报,2005,24(3):107-109.

[3]北京大学数学系几何与代数教研室代数小组.高等代数[M].北京:高等教育出版社,1988.

[4]钱吉林.高等代数题解精粹[M].北京:中央民族大学出版社,2002.

[5]屠伯埙,徐诚浩,王芬.高等代数学[M].上海:上海科学技术出版社,1987.

[编辑]张涛

O151.2

A

1673-1409(2014)19-0011-03

2014-02-15

国家自然科学基金资助项目(11201039;61273179);湖北省教育厅重点项目(D20101304)。

呙林兵(1970-),男,硕士,副教授,现主要从事矩阵论方面的教学与研究工作。