滑模控制在变载荷高性能系统中的应用

王金鹏，吴向东，张兵，陆世荣，李波

(西南交通大学机械工程学院，成都 610031)

滑模控制在变载荷高性能系统中的应用

王金鹏，吴向东，张兵，陆世荣，李波

(西南交通大学机械工程学院，成都 610031)

为比较传统的PID控制与滑模控制(SMC)在非线性变化的变载荷负载条件下在控制性能方面的差异，通过搭建PID与SMC控制器模型、永磁同步电机(PMSM)控制模型以及运动机构及负载模型，构建了整个控制测试平台。在此平台下使用Matlab与ADAMS软件联合仿真，对2种算法的控制性能进行分析。经比较发现:滑模控制较PID控制在控制精度、调节时间、鲁棒性及能量控制等方面均具有一定的优越性。

滑模控制;PID控制;变载荷;性能仿真

机电控制系统中，变载荷负载的运动特性主要表现在外部负载的运动突变、运动模型转动惯量的突变以及机械谐振等方面。在机电控制系统的整个运动控制过程中，由于变载荷负载的状态及整个运动系统转动惯量存在较大变化，故模型很难准确、全面地反映整个运动控制过程中运动对象的运动特性［1］。同时，变载荷负载的非线性变化特性加强了整个机电控制系统的非线性，使得变载荷情况下高性能控制更加复杂，控制难度更高。

传统PID控制存在积分饱和与微分突变现象，这一缺陷使得在对变载荷负载进行控制时，对是否能够达到较高控制性能提出了疑问。滑模控制(SMC)作为一种先进的控制理论，经过多年发展已形成一个相对独立的研究分支，是目前自动控制系统领域一种常见的设计方法［2］。在滑模控制中，滑动模态可进行设计且与对象参数及扰动无关，所以滑模控制使系统在受到参数摄动和外部干扰时具有不变性。同时，滑模控制还具有响应快速、无需系统在线识别、物理实现简单等优点［3-4］。这些特性使得滑模控制在非线性系统及伺服系统方面得到广泛应用。

本文以所设计的变载荷运动控制系统为控制对象，通过引入滑模控制，与传统的PID控制进行比较，分析其在控制精度、调节时间、鲁棒性、能量控制等方面的特点，验证滑模控制在变载荷高性能系统中的可行性。

1 滑模变结构控制基本原理

滑模变结构控制的基本原理为:根据系统所需控制性能，在系统状态空间中设计出开关面(状态空间不连续曲面)，通过滑模控制器使系统状态向量从开关面之外向开关面收束。当系统状态向量到达开关面后，反馈控制的作用将发生变化，使系统性能达到期望指标。

滑模变结构控制与常规控制的根本区别为其在变控制率和系统结构在滑模面上的不连续性，即随时间变化的开关特性。该特性使控制系统在一定特性下沿规定的状态轨迹做小幅度、高频率的上下运动。由于滑动模态是预先设计的，系统对于参数变化及外部扰动不敏感，因此处于滑模运动的系统具有很强的鲁棒性。

2 变载荷系统模型介绍

2.1 整体模型搭建

在搭建运动机构与负载的物理模型时，采用西南交通大学李波的设计模型［1］。该模型的设计思路为:使用工程软件(SOLIDWORK、ADAMS)，依据工程参数创建出所需模型，并在软件中对模型进行参数设置，使其尽量贴近实际工程运动情况。

该模型采用的装置主要包括交流伺服电机及伺服电机控制器、减速器、负载固定盘、负载、编码器等，如图1所示。所涉及的各种运动机构的质量及转动惯量如表1所示。

图1 变载荷控制系统模型

表1 各机构参数

2.2 ADAMS软件下的变载荷模型

2.2.1 变载荷仿真物理模型

因模型支撑架部分对仿真结果没有影响，故在ADAMS软件中仿真时对整个模型进行简化处理，只载入运动机构及负载部分以便于仿真。模型的各项参数设置与实物参数基本相同，其变载荷模型如图2所示。

图2 变载荷模型

2.2.2 变载荷模型控制参数

在变载荷运动控制系统中，主要对负载运动位置角度实现精确控制。在ADAMS软件中，变载荷负载主要表现为在给定时刻改变负载的质量及其转动惯量。整个变载荷运动控制系统的运动规律为:交流伺服电机带动负载固定盘和6个负载转动，固定盘每隔一段时间抛出一个负载，抛出后继续旋转直至将6个负载全部抛出。控制模型中负载的转动惯量变化趋势如图3所示，对负载旋转位置的角度位置要求如图4所示。

图3 负载转动惯量

图4 负载旋转角度

2.3 交流伺服电机模型

交流伺服电机控制模型通过Matlab下的SIMULINK模块搭建。因ADAMS模型采用力矩输入，故交流伺服电机模型采用力矩输出控制。

根据电机学理论可得，电机转速与转矩间的传递函数为

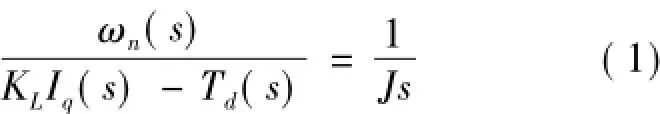
式(1)中:ωn为电机转子机械角频率;Td为负载转矩。

加入速度和电流各环调节器的传递函数模块后，可在Matlab软件中构建出永磁同步电机调速系统的动态结构图，如图5所示。其中，βi为电流反馈系数，αn为速度反馈系数［6］。在Matlab中搭建的伺服电机运动模型如图6所示。

图5 永磁同步电机调速系统动态结构

图6 伺服电机运动模型

2.4 滑模变结构位置环调节器设计

式(2)、(3)中:θd(t)为给定角度信号;θ(t)为角度反馈信号。设计位置环滑模函数为

其中，c满足Hurwitz条件，即c＞0。滑模变结构调节器输出为

位置环滑模变结构调节器结构如图7所示［8］，Matlab中搭建的滑模控制模型如图8所示。

图7 位置环滑模变结构调节器结构

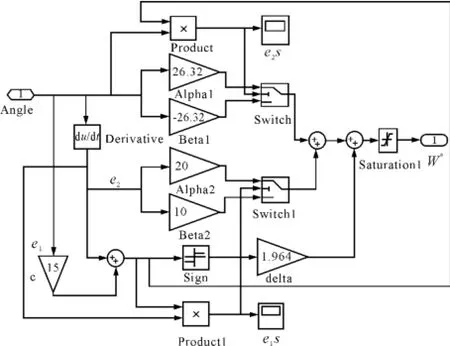
图8 滑模控制模型

3 SMC与PID控制性能比较

将ADAMS软件下的运动机构与负载模型集成到Matlab软件中。设置好各项参数后，通过与Matlab进行联合仿真来对SMC性能与传统的PID控制性能进行比较。

考虑到电机实际工作情况，需对电机的瞬时最大电流、转速及输出转矩进行限幅设置(瞬时最大电流为7.8A，最高转速为5 000 r/min，最大输出转矩为3.82 N·m)。同时为保证仿真结果具有可比性，在模型中加入能量检测单元。集成后的PID控制模型与滑模控制模型分别如图9、10所示。

图9 PID控制模型

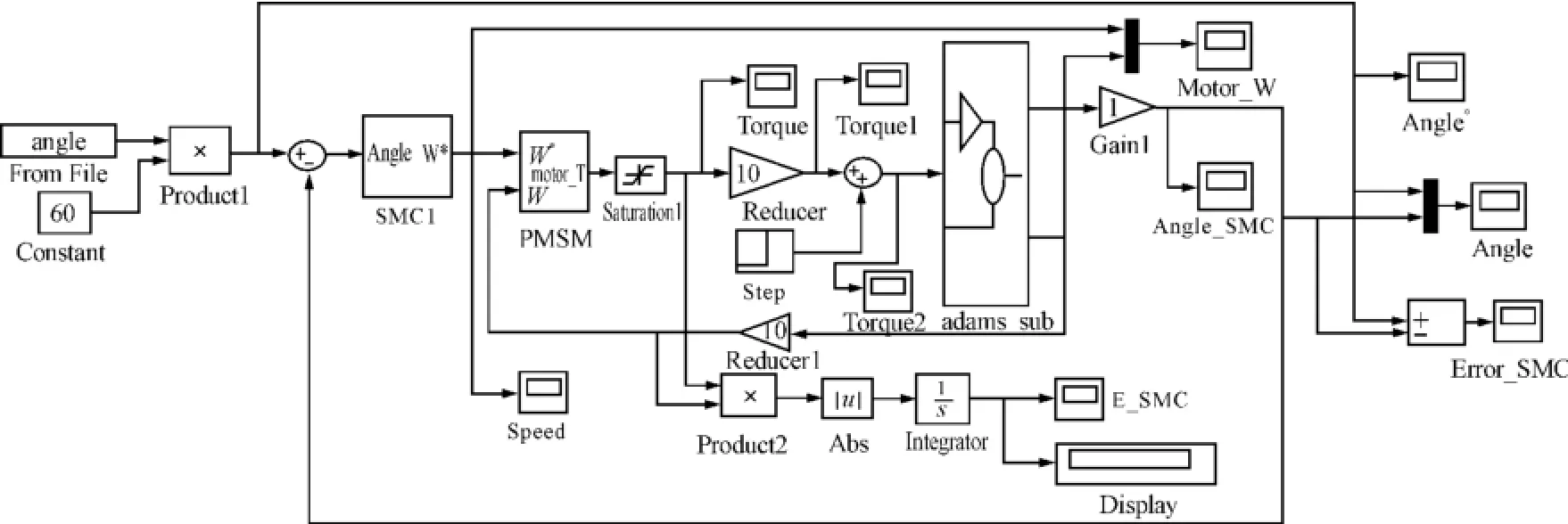
图10 滑模控制系统模型

对于传统PID控制与滑模控制主要通过以下几个方面进行比较。

3.1 PID与SMC固定负载条件下对阶跃输入的响应

将负载模型调整为固定载荷，验证PID与SMC在阶跃输入下的反应情况。对模型输入幅值为60的阶跃信号后，5 s时间内能量输出均为100 J时，PID与SMC两种模型的角度响应曲线与位置误差曲线分别如图11、12所示。

从图11、12可看出:在输出能量相同的情况下，两者均能实现对角度的较好跟随。但对误差曲线放大后可看出:PID控制误差在-0.025°～-0.02°，而SMC误差在±0.005°以内，说明在高精度控制条件下，SMC在控制精度方面表现更优。

图11 PID/SMC定载荷角度曲线

3.2 PID与SMC变载荷负载条件下的响应

为验证PID与滑模变结构两种控制算法对不同负载情况的适应性，两种模型均选用与固定负载条件下相同的参数。仿真结果如图13、14所示。

图12 PID/SMC定载荷位置误差曲线

图13 PID/SMC变载荷角度曲线

图14 PID/SMC变载荷角度误差曲线

从图13、14可看出:PID与SMC在变载荷负载条件下均能够对目标曲线进行较好跟随。但通过误差曲线可发现:PID控制误差范围在±3°以内，而SMC误差范围在±0.6°以内。能量方面，PID控制下系统总输出能量为805.8 J，SMC控制下系统总输出能量为798.4 J，PID能量输出稍大。

3.3 PID与SMC变载荷负载加入突变转矩下的响应

为检测PID与SMC的抗干扰能力，在时间为80 s时加入35.5 N·m的阶跃转矩信号，对仿真结果进行分析。仿真结果如图15、16所示。

图15 突变转矩下PID/SMC变载荷角度误差曲线

由图16、17可看出:当加入阶跃转矩后，PID与SMC在角度误差上均有较大变化。其中PID角度最大误差为11.9°，SMC角度最大误差为6.4°。PID恢复到正常误差范围的时间为2 s，SMC恢复到正常误差范围的时间为0.6 s。从能量曲线上看，在未加入阶跃转矩前，两控制算法对能量的使用情况非常接近;加入阶跃转矩后PID控制的能量输出相比SMC控制有增加。在能量输出方面，PID为1.325×104J，SMD能量输出为1.316× 104J。

当对系统加大干扰力矩(增加为40 N·m)时，SMC随瞬时误差较大，但仍能够保持对系统的控制，而PID控制已经失稳，如图17、18所示。

图17 PID变载荷角度误差曲线

图18 SMC变载荷角度误差曲线

4 结束语

1)在变载荷运动控制系统的高精度控制要求下，SMC在位置控制方面相比传统PID控制精度更高。

2)当角度误差较大时，SMC相对传统PID控制将误差调整到常规状态的调节时间更短。

3)当负载变化较为复杂时，SMC相比传统PID控制的鲁棒性更强。

4)当负载变化较为平稳时，传统PID控制与SMC在能量输出方面性能比较接近。但当负载变化较快时，SMC在能量控制方面较传统PID更为节约。

综上所述，滑模控制的开关特性使其能在不同控制结构间进行切换，负载变化较大时依然能够获得较好的控制性能。PID控制则由于积分饱和、微分突变现象导致其控制性能受到一定限制。因此，在对变载荷负载进行高性能控制时，滑模控制相比传统PID控制在控制精度、调节时间、鲁棒性及能量控制方面更具有优越性。但由于时间滞后、空间滞后及系统惯性的影响，滑模控制会产生一定的高频抖振，在应用时应引起注意。

［1］李波.PDF策略在变载荷高性能控制系统中的设计及仿真［J］.工程设计学报，2013(1):49-54.

［2］张晓宇，苏宏.滑模控制理论进展综述［J］.化工自动化及仪表，2006，33(2):1-8.

［3］刘金琨，孙富春.滑模控制理论及其算法研究与进展［J］.控制理论与应用，2007，24(3):407-418.

［4］刘金琨.滑模控制Matlab仿真［M］.北京:清华大学出版社，2005.

［5］廖晓钟，刘向东.控制系统分析与设计［M］.北京:清华大学出版社，2002.

［6］陈先锋，舒志兵，赵英凯.基于PMSM伺服系统的数学模型及其性能分析［J］.机械与电子，2005(1):41-43.

［7］严彩忠，舒志兵.变加减速算法在位置伺服系统中的应用与分析［J］.机械制造，2007(1):15-16.

［8］陈先锋.PMSM位置伺服系统的分析设计及其应用研究［D］.南京:南京工业大学，2005.

(责任编辑 杨黎丽)

Control System Design and Simulation in Variable Load High-
Performance System with Sliding Mode Control

WANG Jin-peng，WU Xiang-dong，ZHANG Bing，LU Shi-rong，LI Bo
(School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China)

sliding mode control;PID control;variable load;performance simulation

:In order to compare the control performance differences between the traditional PID control and sliding mode control(SMC)in the non-linear changes variable load，a control test platform which includes PID/SMC controller model，permanent magnet synchronous motor(PMSM)motor control model，and a movement mechanism and load models were built.In this platform，through the software co-simulation of MATLAB and ADAMS，a detailed analysis on the performance of both was done which was based on the control performance of the two control algorithms.By comparison，the sliding mode control can be found better than traditional PID control in the control precision，adjustable time，robustness and energy control.

10.3969/j.issn.1674-8425(z).2014.06.010

2014-02-26.

中央高校基本科研业务费专项资金创新项目(SWJTU11CX024)

王金鹏(1988—)，男，硕士研究生，主要从事机电液一体化及控制系统建模仿真研究。

王金鹏，吴向东，张兵，等.滑模控制在变载荷高性能系统中的应用［J］.重庆理工大学学报:自然科学版，2014(6):53-59.

format:WANG Jin-peng，WU Xiang-dong，ZHANG Bing，et al.Control System Design and Simulation in Variable Load High-Performance System with Sliding Mode Control［J］.Journal of Chongqing University of Technology:Natural Science，2014(6):53-59.

TH122

A

1674-8425(2014)06-0053-07