3种计算渗透率变异系数方法的对比

2014-06-27桂东旭中石油大庆油田有限责任公司勘探开发研究院黑龙江大庆163712

长江大学学报(自科版) 2014年26期

桂东旭 (中石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆 163712)

3种计算渗透率变异系数方法的对比

桂东旭 (中石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆 163712)

渗透率变异系数是描述油藏宏观非均质性的一个重要参数,目前有计算渗透率变异系数的方法有统计学理论公式法、Dykstra-Parsons定义法和lorenz系数法3种,通过详细介绍并对比不同方法的计算步骤与原理,给出了每种方法的优缺点和适用范围,并以东部层状砂岩油田7个处于特高含水开发阶段的区块为例进行验证和比较。结果表明,统计学理论公式法与Dykstra-Parsons定义法得到的结果与实际地质认识稍有不同,lorenz系数法与地质认识相一致。通过理论与实际对比分析推荐采用lorenz系数法来计算渗透率变异系数。

渗透率;变异系数;计算方法

储层宏观非均质性是储层非均质性的重要组成部分,主要是指储层岩性、物性、含油性以及砂体连通程度在纵向和横向上的变化特征,其中渗透率的变化对储层的宏观非均质性来说是一个重要影响因素,渗透率变异系数是表征储层渗透率非均质性的一个重要参数,也是影响油田采收率的一个重要因素,在油藏工程和地质研究中有着广泛的应用[1-2]。目前主要有3种计算渗透率变异系数的方法,笔者对每种计算方法的计算步骤、原理和适用范围进行了评价对比,并以东部层状砂岩油田进入特高含水阶段的7个区块为例进行验证和比较,为合理准确测算渗透率变异系数和选择计算方法提供技术依据。

1 渗透率变异系数的含义

渗透率变异系数反映储层渗透率非均质程度,表示围绕渗透率集中趋势的离散程度。一般来讲,渗透率变异系数大于0,其值越小,表明均质性越强;其值愈大,则表明非均质性愈强[3-4]。目前有3种计算渗透率变异系数的方法。

2 统计学理论公式法

标准变异系数[5]是一组数据的变异指标与其平均指标之比,它是一个相对变异指标。变异系数有全距系数、平均差系数和标准差系数等。常用的是标准差系数,用CV表示,即标准差与均值的比率,变异系数又称离散系数,反映单位均值上的离散程度。

变异系数的计算公式为:

式中,CV为变异系数;σk为样品渗透率标准差,m D;¯k为样品渗透率平均值,m D;n为样品数量; ki为第i个样品的渗透率,m D,h为有效厚度,m;hi为第i个样品的有效厚度,m。

在油田实际生产中,平均渗透率通常根据自然电位等测井曲线资料对所钻井所遇各油层得到的渗透率,利用单井各小层有效厚度加权平均得到。

该方法的优点是适合于任何渗透率分布类型;缺点是所计算的CV值在0～∞,难于确定其非均质状况。其改进方法是对所得结果进行数据处理,使CV值处于0～1,进而得到相对的非均质强弱状况。

3 Dykstra-Parsons定义法

Dykstra和Parsons于1950年引入了渗透率变异系数Vk的概念[4],它是一组非一致性的统计度量数据。一般用于描述渗透率属性,但也可延伸到处理其他岩石物性。一般认为渗透率数据是按对数正态分布的,也就是说,形成油藏岩石渗透率的地质过程,使得渗透率围绕几何均值分布。Dykstra和Parsons认识到了这一特性,并引入了渗透率变异的概念来表征这种分布,确定变异系数Vk需要的计算步骤如下:

1)按渗透率递减即下降顺序排列岩石样品。

2)对每一样品,计算渗透率大于这一样品的厚度百分比。

3)在对数概率图纸上,将渗透率作为对数轴,厚度百分比作为概率轴,做出点图。

4)通过这些点画一条最佳直线。

5)读取厚度的比例为84.1%和50%时对应的渗透率值,记为K84.1和K50。

6)Dykstra-Parsons定义的渗透率变异系数Vk用式(4)计算:

式中,K50为岩石样品数量累积频率等于50%时对应的渗透率值,也称概率平均渗透率,m D;Vk为渗透率变异系数;K84.1为岩石样品数量累积频率等于84.1%时对应的渗透率值,mD。

该方法的优点是可计算的Vk在0～1之间;缺点是只适合于渗透率呈对数正态分布的类型,实际应用中曲线难接近于一直线。此外,也有用岩石样品数量百分比频率来代替厚度百分比作为概率轴进行计算的。当前理论研究和应用中用此种方法计算渗透率变异系数的已不多,或应用渗透率级差与渗透率突进系数等类似参数代替其进行表征。

4 Lorenz系数法

基于洛伦茨曲线的基尼系数是意大利经济学家1922年提出的定量测定收入分配差异程度的指标[6]。洛伦茨曲线是国际上公认可以用来描述社会某种收入分配差异程度的一种比较直观的方法。Schmalz和Rahme于1950年将其引入成为一个描述储层非均质性的参数,称为劳伦兹系数,其取值介于完全均质系统的0和完全非均质系统的1之间,可用以下步骤计算劳伦兹系数:

1)将所有可能得到的渗透率值以递减顺序排列。

2)计算累积地层系数∑Kh(渗透率K与有效地层厚度h的乘积之和)和∑φh(孔隙度φ与有效地层厚度h的乘积之和)。

3)将这2个累积参数进行标准化,使其介于0～1之间。

4)将标准化的∑Kh和标准化的∑φh画在笛卡尔坐标系上。5)劳伦兹系数L定义如下式:

式中,SABC为曲面三角形ABC的面积,m2;SACD为三角形ACD的面积,m2;劳伦兹系数L在0～1之间变动;0表示完全均质;1表示完全非均质。

图1表示的是一油层流动能力的分布。完全均质系统的渗透率各处完全相等,因此标准化的∑Kh和∑φh图为一直线。图1表明随渗透率的高低值差别的增大,图像向左上角显示更大的凹度,这说明非均质性更强。也就是说,偏离直线的严重程度是非均质性的量度,由此可通过计算劳伦兹系数定量描述储层的非均质性。为了使计算简便,更为常用的是将渗透率从大到小排队成一序列,根据岩石样品数量累积百分比频率和渗透率累积百分比绘制成劳伦兹曲线进行计算。该方法优点是适合于任何渗透率分布类型,又使计算的Vk值在0～1之间。

对Wamen和Price于1961年提出的对数正态渗透率分布来说,渗透率变异系数和劳伦兹系数之间的关系,数学上可用以下2公式来表示:

1)用渗透率变异系数表示的劳伦兹系数:

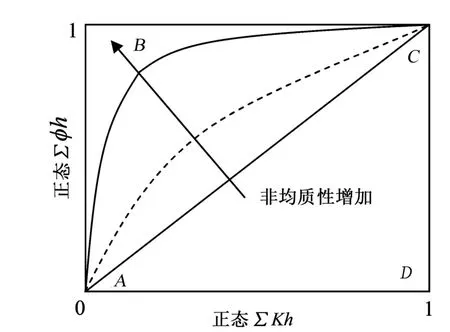
图1 标准化的流动能力

5 实例应用

表1 东部某油田渗透率变异系数计算结果

根据以上的计算原理和方法,应用VB6.0编制了应用程序,分别应用统计学理论公式法、Dystra-Parsons法和Lorenz系数法计算了东部层状砂岩油田7个已经进入特高含水开发阶段区块的渗透率变异系数,结果如表1所示。

地质研究表明,非均质性由强到弱的顺序为:3区和4区最大,其次是5区和6区,再次是1区和2区,最小的是7区。由计算结果可以看出,其中Lorenz系数法得到的计算结果与实际认识基本相一致,Dystra-Parsons定义与统计学理论公式法与实际认识稍有差距,因此推荐应用Lorenz系数法来计算渗透率变异系数。