高速铁路接触线磨耗对接触网静态形状的影响

侯权玲，吴积钦，关金发

0 引言

接触网是为高速列车传输电能的静态设备，也是受电弓运行的滑道，因此受电弓滑板和接触线之间的磨耗是客观存在的。磨耗不断增加的过程，可能导致断线等一系列的弓网事故。欧标EN50119：2009在接触网设计中，计算接触线最大拉断力时，考虑了最大磨耗系数为0.2[1]。因此，监测接触线磨耗使其在没有达到断线可能前更换接触线尤为重要。目前，与接触线磨耗监测相关的文献比较多，如文献[2、3、4、5]分别介绍采用不同方法对接触线磨耗的监测。但是，在接触线允许磨耗下，接触线磨耗是否对接触线静态几何形态以及受电弓与接触线动态耦合效果的影响没有得到论证。本文利用经典力学方法对定位点受力分析[7，8]、吊弦与接触网的连接处受力分析[7～9]以及应用一些常见接触网找形方法[10，11]，研究接触线磨耗对接触网静态几何形态的改变，再通过对比有限元仿真结果，验证该计算方法的准确性。

1 无磨耗接触网状态的计算

为了方便研究接触网几何形态，建立如图1所示的x-y坐标系。

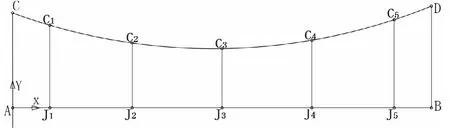
图1 接触网状态图

1.1 接触线形态

一个跨距内的接触线水平方向受接触线张力（Tj）；垂直方向的吊弦力 F(i)（i = 1，2，…，n），定位器的支持力（FA、FB）以及自身重力（gj），接触线静态状态如图2所示。

图2 接触线静态状态图

根据接触线与吊弦连接处Ji的坐标（xi，yi），再对两连续悬挂点使用不等高悬挂的轨迹公式即可获得接触线的几何形状。因此，第i-1根吊弦到第i根吊弦的接触线轨迹公式为

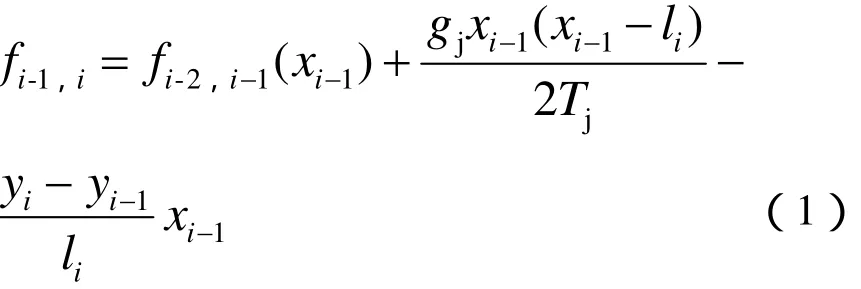
式中，gj为接触线单位荷载，li为第i-1根吊弦到第i根吊弦的水平距离。下标i为0是指定位器处。

1.2 吊弦力

吊弦承担接触线自重和自身重量（忽略不计），受力分析如图3所示，f1、f2分别指前后两段接触线对Ji处垂直方向的力。

图3 接触线与吊弦连接处Ji受力分析图

因此，第i根吊弦的吊弦力为

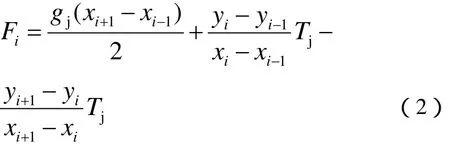
1.3 承力索形态

承力索的几何状态和受力情况如图4所示，承力索主要受自重和吊弦力的影响，因此腕臂对承力索的支持力FD、FC为

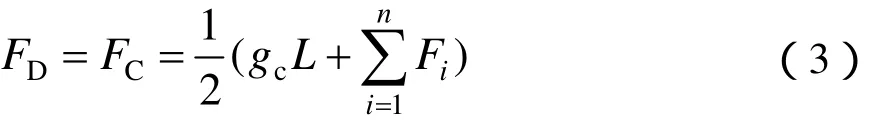
式中，gc为承力索单位荷载，L为接触网跨距。

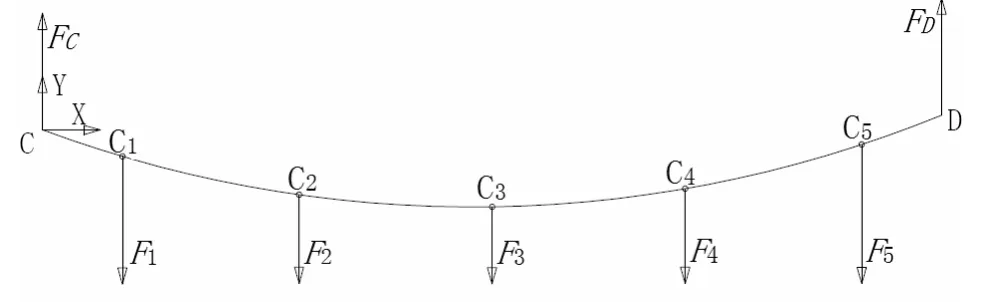
图4 承力索静态形状示意图

由于静态平衡下抛物线单元节点处的力矩为0，则：

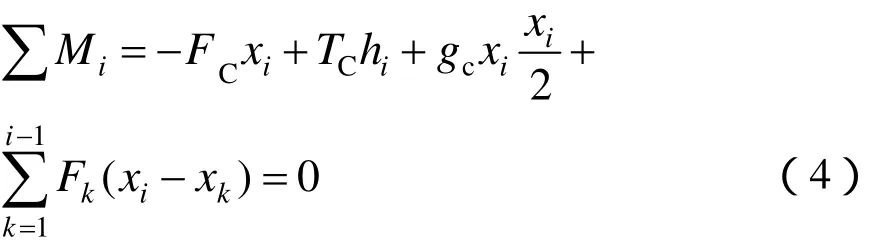
由式（4）计算得到第 i根吊弦距承力索支撑点的垂向位移 hi为

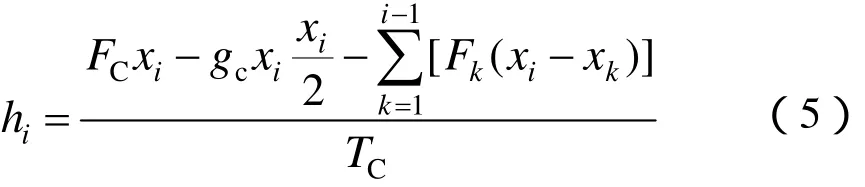
因此，承力索与吊弦连接处的纵坐标 yi′为

式中，h为接触网结构高度。吊弦长度 di为

同样，知道承力索与吊弦连接处 Ci的坐标（ xi， yi′），再对两连续悬挂点使用不等高悬挂的轨迹公式即可获得承力索的几何形状。因此，第i-1根吊弦到第i根吊弦的承力索轨迹公式为

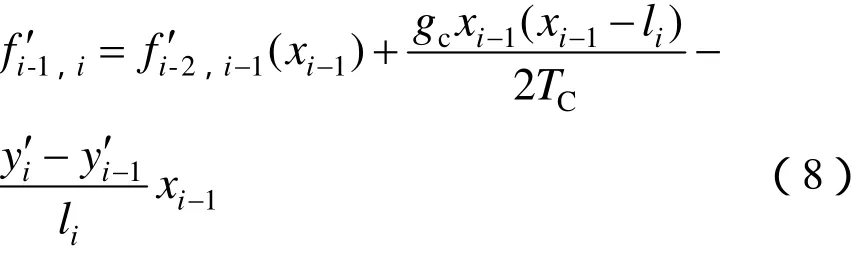
2 不同磨耗下接触网状态的计算

在计算不同磨耗下接触网状态时，因为考虑是均匀磨耗，计算接触线状态时接触线重量乘以（1-α），α是指接触线磨耗下截面积与接触线总截面积的比值，简称磨耗系数。

接触网在磨耗下受力分析和结构变化如图 5所示，虚线是指磨耗下的接触网状态，实线是无磨耗时接触网状态：

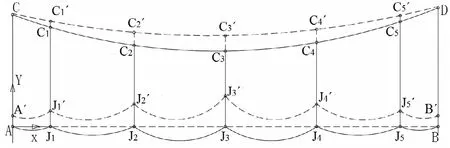
图5 存在磨耗接触网状态变化图

设第i根吊弦处磨耗后上升量为Δyi，对吊弦与接触线连接处Ji合力为零有：

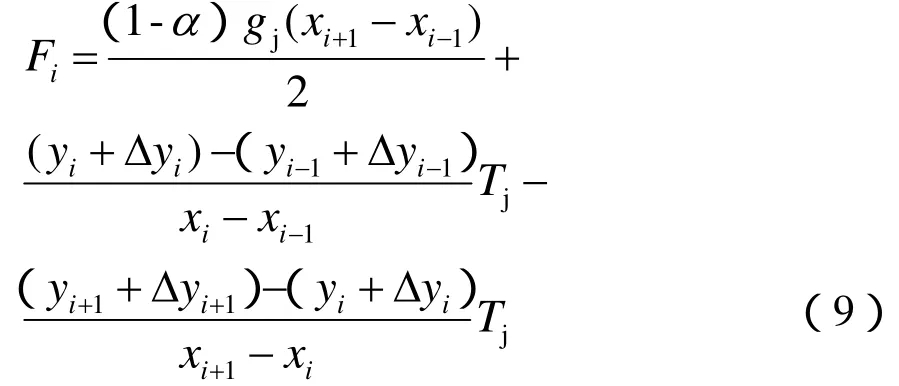
对吊弦与承力索连接处Ci合力为零：

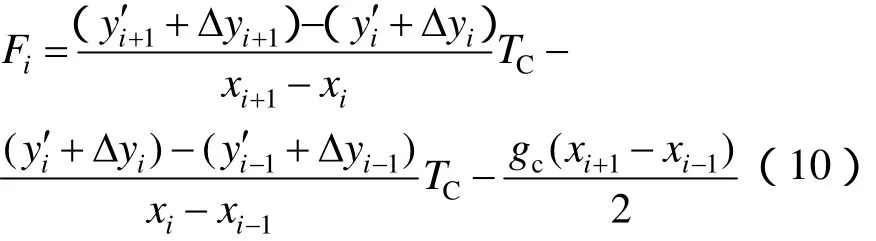
定位器与接触线的连接处，定位器的抬升与定位器垂直方向的力的对应关系：

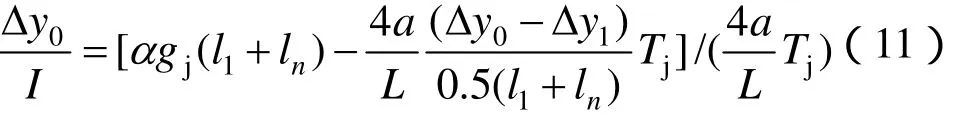
式中，I为定位器的长度，a为拉出值的绝对值。

联合式（9）—式（11）可以解得Fi和Δyi，知道每个节点上升的距离Δyi，就可以确定不同磨耗下接触网的状态。

3 计算算例

下面以京津城际接触网为例具体研究磨耗对接触网的影响，该接触网具体参数见表1。

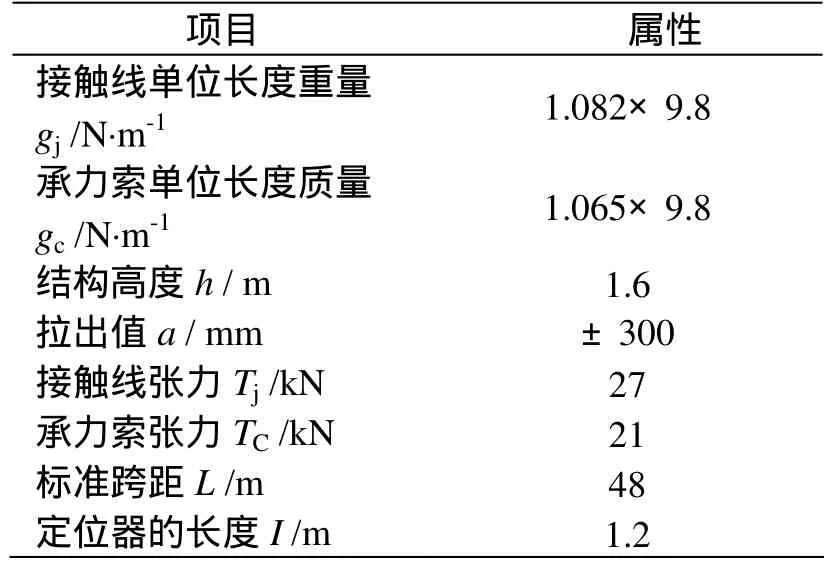
表1 京津城际接触网设计参数表

由表中数据可知线路跨距为48 m，每个跨距内有5个吊弦，又因为l1= l5= 5 m，所以吊弦之间的间距为9.5 m。因此，x0= 0，x1= 5，x2= 14.5，x3= 24，x4= 33.5，x5= 43，x6= 48。

3.1 无磨耗接触网状态计算

首先，根据悬挂类型可知接触线与吊弦的连接处Ji的坐标，如表2所示。根据式（1）画出接触线的几何形态如图6所示。

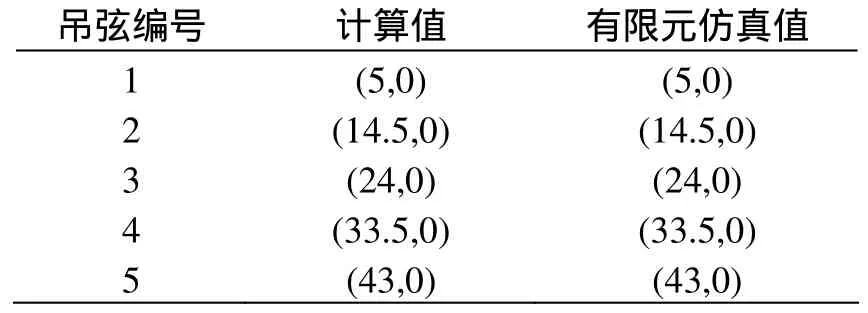
表2 无磨耗时接触线与吊弦的连接处Ji的坐标值表

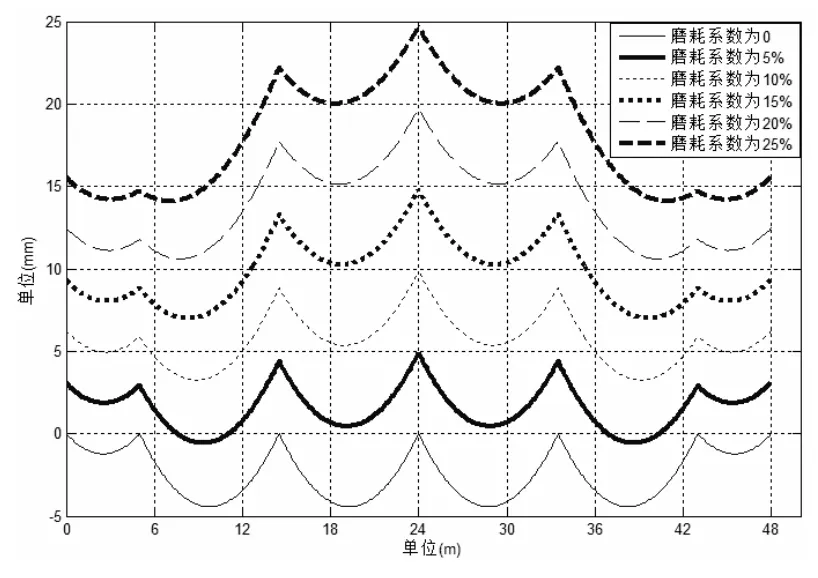
图6 不同磨耗下接触线的形态图

将接触线与吊弦连接处Ji的坐标代入式（2），即可计算出每个吊弦的吊弦力Fi，如表3所示。

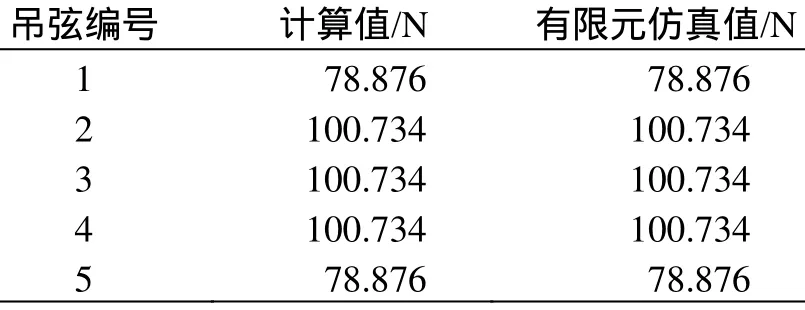
表3 无磨耗时吊弦力Fi统计表

将吊弦力代入式（3）可以计算出，腕臂对承力索的支持力FC= FD= 478.466 N。将FC、Fi和xi代入式（5）、式（6）可计算出承力索与吊弦连接处Ci的坐标，如表4所示。将Ci的坐标代入式（8）画出承力索几何形态如图7所示。

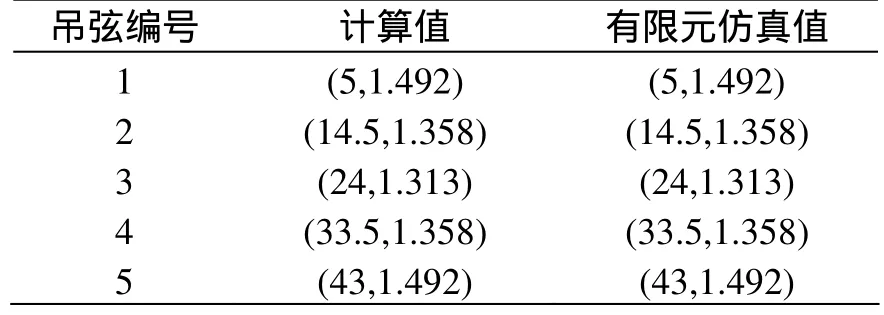
表4 无磨耗时承力索与接触线连接处Ci的坐标值表

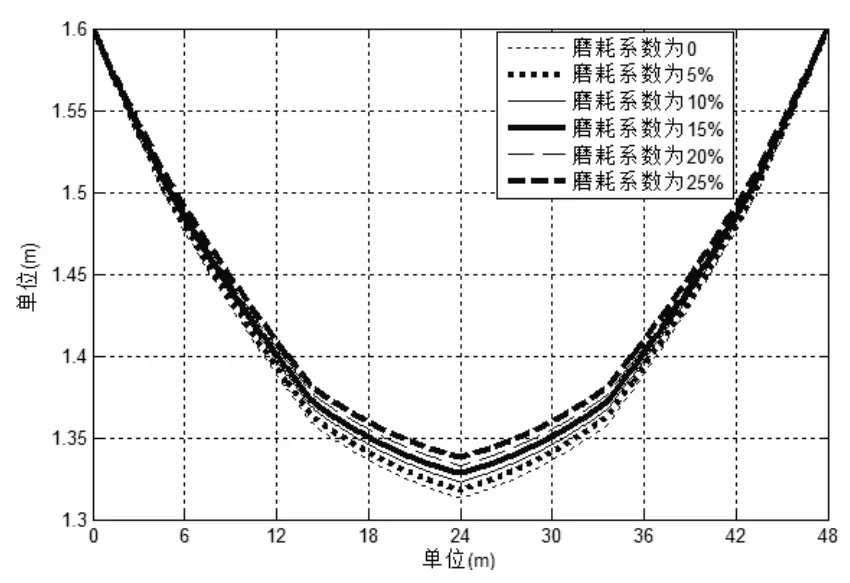
图7 不同磨耗下承力索的形态图

3.2 磨耗系数为α 时接触网状态

将数据代入式（9）—式（11）可以求得不同磨耗下，接触网上升的变化量和吊弦力，如表5所示。定位器和接触线连接处上升量，如表6所示。

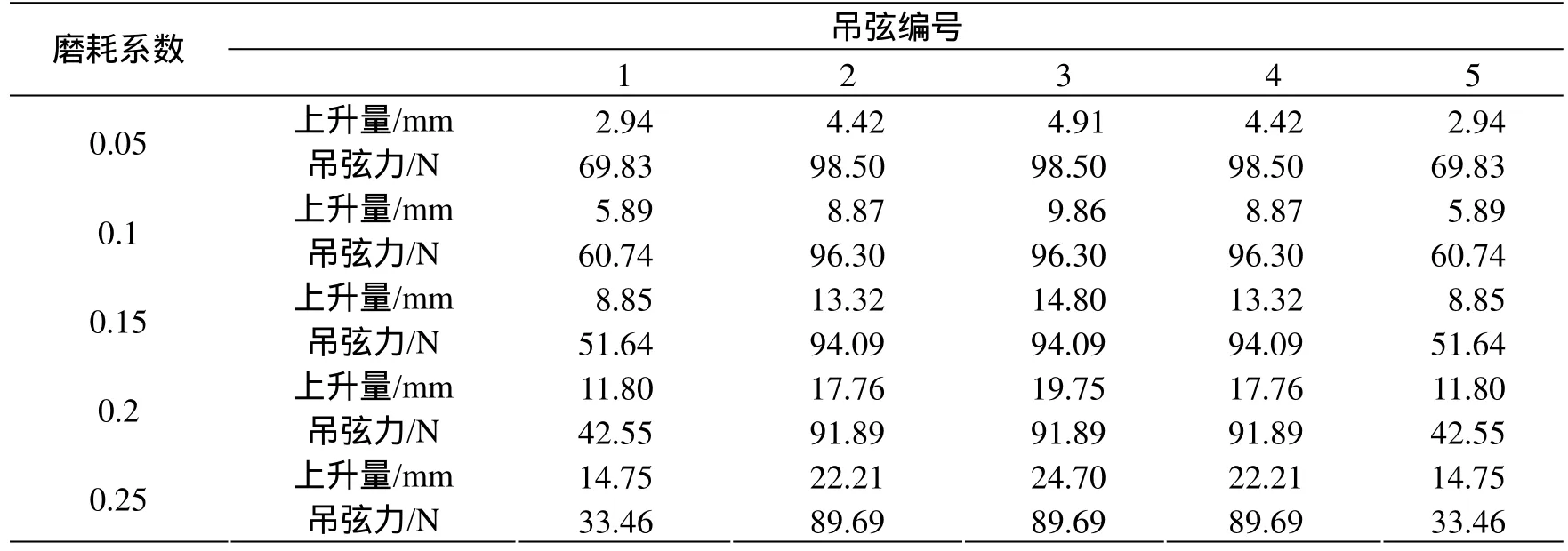
表5 不同磨耗接触网上升量和吊弦力统计表

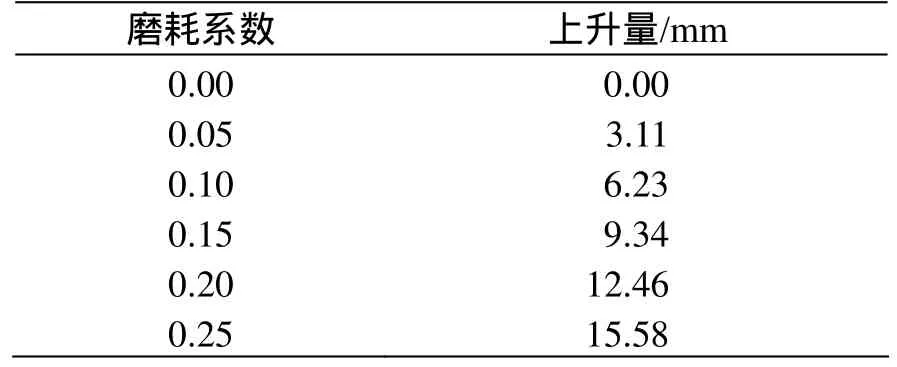
表6 不同磨耗下定位器和接触线连接处上升量数值表

根据计算结果，接触线在不同磨耗下几何形态，如图6所示，承力索在不同磨耗下几何形态，如图7所示。

3.3 磨耗后接触网的理想状态计算

磨耗后接触网理想状态是指以磨耗后接触线重新搭建接触网，进行该网的理想状态计算时，接触线的重量取其磨耗后的质量，其他参数不变，按照第1节无磨耗接触网状态的计算方法计算即可。

以磨耗系数为 0.20接触网理想状态为例，计算结果如表7所示，接触线形态如图8所示。

根据计算结果可知磨耗后接触网理想状态下接触线的几何形态和原始接触线形态近似相同，可见磨耗后接触网理想状态可以满足接触网受流的要求。根据接触网2种不同状态下吊弦长度差异可以看出，适当的增长吊弦长度可以调节由磨耗引起的接触网状态变化问题。

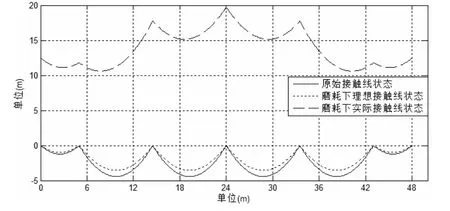
图8 不同工况下接触线的形态对比图

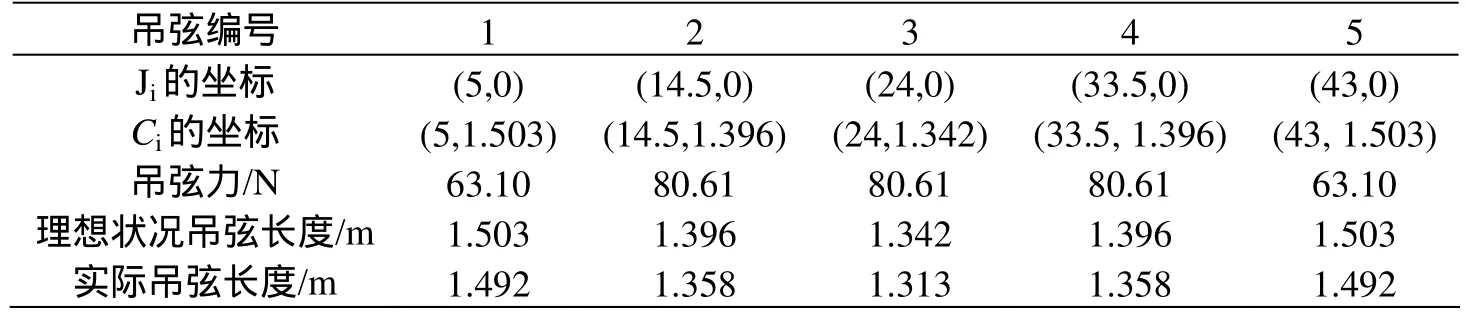
表7 20%磨耗接触网理想状态参数表

4 结论

（1）通过对无磨耗接触网状态的计算，推导出无磨耗下接触线、承力索静态形状的计算方法，并给出吊弦长度计算公式。

（2）通过对不同磨耗系数下接触网状态计算，利用节点平衡的方法确定变化后接触网状态，这种方法能有效的计算接触网局部改变后整个接触网的形变量以及接触网终态。

（3）根据研究可以看出，高铁接触线磨耗对接触网几何形态的确有明显的改变，使接触网整体都有不同程度的抬升。由于接触网各处抬升的量不同，导致接触线的平顺度下降会影响接触网受流。由于磨耗导致的抬升加上受电弓引起的抬升，可能影响弓网安全配合，因此还需深入研究。

（4）接触线磨耗会使接触网整体结构形状发生改变，使各个吊弦力之间差异增大，中间吊弦的吊弦力增大，靠近定位装置吊弦的吊弦力减小。

（5）应用本文研究的计算方法，对考虑磨耗情况下接触网的设计、施工和维护有一定指导意义。

[1]EN50119: Railway applications – Fixed installations –Electric traction overhead contact lines[S], Brussels CENELEC, 2009.

[2]阎玲玲. 基于表面温度法的接触线磨耗红外诊断[J].机电工程，2011，（12）：1426-1429.

[3]毕铁艳. 电力机车接触线动态磨耗检测技术研究[D].大连交通大学，2005.

[4]彭朝勇. 便携式接触线几何参数检测系统[J].电气化铁道，2007，（4）：26-28.

[5]张忠杰. 接触线磨耗图像检测研究[J].西铁科技，1996，（S1）：118-122.

[6]吴燕. 高速受电弓---接触网动态性能及主动控制策略的研究[D].北京交通大学，2011.

[7]于万聚. 高速电气化铁路接触网[M].成都：西南交通大学出版社，2003.

[8]吴积钦. 受电弓与接触网系统[M].成都：西南交通大学出版社，2010.

[9]董昭德. 接触网[M].北京.中国铁道出版社,2010.

[10]方 岩. 高速接触网整体吊弦预配[J].西南交通大学学报，2010（5）：763-767.

[11]刘大勇. 基于索网找形的接触网吊线长度计算方法研究[D].西南交通大学，2009.