位移共振与速度共振之别
2014-06-27郑金
郑 金
(凌源市职教中心 辽宁 朝阳 122500)
在机械振动中,共振现象包括两种,即位移共振和速度共振;在电磁振荡中,共振现象也包括两种,即电压共振和电流共振,统称为电谐振.那么位移共振与速度共振有何异同?电压共振与电流共振相当于机械振动中的哪种共振?下面举例分析.
1 机械振动中的位移共振和速度共振
物体在弹簧弹力和正比于速度的线性力作用下的运动为阻尼振动.
【例1】有一个竖直弹簧振子,弹簧的劲度系数为κ,振子为圆盘形,质量为m,其表面与弹簧垂直,在某种液体中上下振动,在运动速度较小的情况下,粘滞阻力的大小与速率成正比,即f=κ′v,若圆盘还受到一个沿竖直方向的周期性外力F′=Fmsinω′t的作用,选择平衡位置为原点,坐标轴竖直向下,设开始向下的初速度为v0,试求振子的位置坐标随时间的变化规律.
解析:对于竖直弹簧振子,当以平衡位置为坐标原点时,重力无影响;再者,振子质量较小,重力可忽略.圆盘形的振子体积较小,受到液体的浮力可忽略不计,以竖直向下为正方向,由牛顿第二定律,有
-κx-κ′v+Fmsinω′t=ma
即
如图3所示,将圆台母线延长,恰交于小活塞中点O,以O为原点建立x轴.
则
所以
设OE=x,则
所以深度E处水的压强为
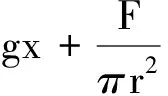
E处长为dx的微元环面积dS为
缸体侧壁所受总压力

所以缸体侧壁所受总力的竖直分力F侧为
F侧=F总sinθ=
8F+136=8F+136 (单位:N)
所以
N=G缸-F侧=
50×10-(8F+136)=
-8F+364 (单位:N)
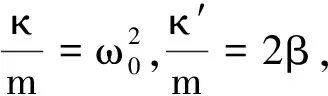
即
齐次微分方程的特征方程为
其两个根为
当阻尼因数较小即β<ω0时,为弱阻尼状态,特征方程有两个共轭复根,即
对该式有两种情况:
(1)无阻尼时,即当β=0时,r=±iω0,振动为无阻尼的受迫振动,这种振动包括两种情形.
其一,若扰动度频率与固有频率不等,即ω′≠ω0,则由高等数学二阶常系数非齐次线性微分方程理论可知,微分方程的通解为
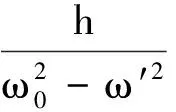
其二,若扰动频率等于固有频率,则微分方程的通解为
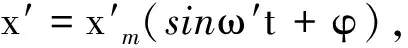
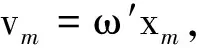
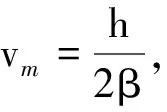
2 电谐振
【例2】如图1所示,有一个电阻R,自感L,电容C和电源E串联组成的电路,其中R,L及C为常量,电源电动势是时间t的函数:E=Emsinω′t,这里Em及ω′也是常量.电源内阻不计.当闭合开关接通电源时,试推导电容器两极的电压随时间变化的微分方程及电谐振条件.
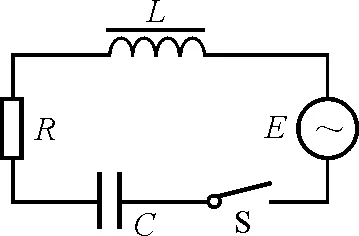
图1
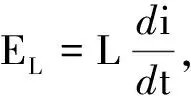
列出回路电路电压方程为
E-EL-uC-uR=0
即
得
化简为
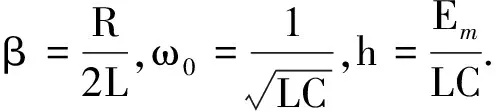
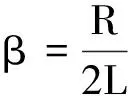
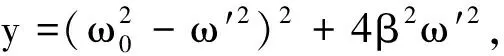
可知函数y最小值的条件是
此时电压幅取得最大值,因此RLC串联电路的电压谐振与机械振动的位移共振相应.
由此可知电流幅取极大值的条件是外界扰动频率ω′与系统固有频率ω0相等,因此电流谐振与机械振动的速度共振相应.
电流谐振现象可通过实验来观察,将RLC串联电路中的电阻元件换为小灯泡,当调节交流电源的频率等于RLC串联电路的固有频率时,即在ω′=ω0的条件小灯泡最亮,表明此时电流最大,即电路中交变电流的有效值最大,发生电流谐振.这是由于谐振时电抗为零,则阻抗最小,即RLC串联电路的等效电阻为纯电阻R.电谐振实质是在交流电通过RLC电路中的电容和电感时,交流电源本身的周期性变化与LC电路充、放电的周期性变化步调一致,即二者固有频率相等,达到稳定状态.
对于串联谐振电路发生谐振的条件,还可通过欧姆定律和阻抗公式及容抗公式来推导.
设电路中交流电源为E=Emsinωt,则阻抗为
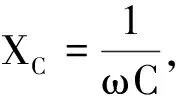
而
令
y=R2ω2C2+(ω2LC-1)2=
L2C2ω4+(R2C2-2LC)ω2+1
这是关于变量ω2的二次函数,有最小值条件是
即
在此条件下,电容器两端的电压的有效值达到最大,电压的峰值也达到最大,因此发生电压谐振.
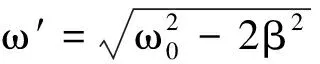
参考文献
1 同济大学数学教研室.高等数学(下册).北京:高等教育出版社,1986.375
2 漆安慎,杜婵英.力学基础.北京:高等教育出版社,1987.432~436
3 周绍敏.电工基础(第三版).北京:高等教育出版社,2005.169
4 吴进校.应如何定义共振.物理通报,2003(9):12
