利用运动模拟绘制点电荷的电场线和等势线

曹 盼(安塞县高级中学 陕西 延安 717400)

电场线和等势线是电场和电势的形象化表示，在研究电学问题中具有重要意义.随着计算机的普及，对精确绘制电场线和等势线有了不少研究[1，2]，不过大都站在大学物理的理论之上，这里试图站在高中物理的基础上进行绘制.

本文的核心思想是根据“电场线上某点电场的方向和该点的切线方向相同”，将问题转化为物体的运动.

1 绘图根据

根据电场线上某点电场的方向和该点的切线方向相同，可知在平面上某点P有

(1)

变形得

(2)

令式(2)等于dt，有

(3)

(4)

此两式就是我们模拟绘制电场线的基础.

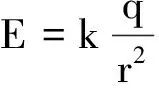
(5)

(6)

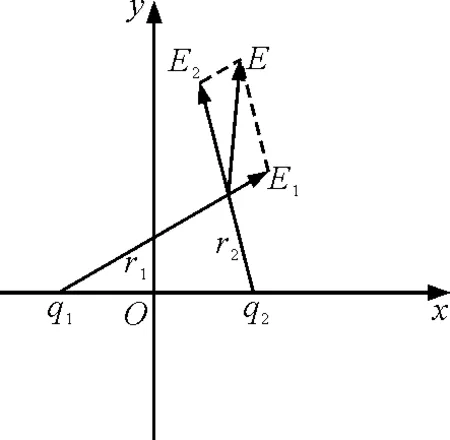
图1 场的叠加

选择一个初位置，根据式(5)、(6)计算物体的速度，然后在“足够短一段时间dt内”按匀速直线运动计算末位置，用直线连接初末位置即为一段电场线(位移、速度和电场方向相同)，从新的位置开始重复计算、绘图直到一个合理的结束条件.

1.1 选初位置

初位置在原则上除了点电荷所在处可以自由选取，但我们不可能在整个区域都画满电场线，因此电场线的绘制是科学和艺术的综合.另外对称的东西要尽量对称地去处理，不要随意破坏任何自然的对称性.由于点电荷的电场线分布是对称的，我们选择从半径为R的圆上开始(左边逆时针旋转右边顺时针旋转).当初位置选好后，由式(5)、(6)两式可知，速度有时为正有时为负，因此物体有时向外走，有时向内走.实际的电场线应该是两个方向都有，为了绘制完整，既要正着走一次(代入dt)也要倒着走一次(代入-dt).

1.2 结束条件[3]

在4种情况下应该结束：

(1)速度太小(设置一个下限eps)；

(2)重复次数太多(增加一个计数器变量counter)；

(3)进入点电荷内部(将点电荷限制在一个小圆之内，半径取R)；

(4)走出可见区域(这里选择一个矩形).

1.3 算法描述

下面给出C/C++语言描述的绘制一条电场线的主要算法片段.

第1步：声明变量eps,R,R0,r1,r2,counter,t,vx,vy,x1,y1,x2,y2;

第2步：给变量赋值eps=1e-16,R=0.4,

R0=2,counter=0,t=0,x1=x0,y1=y0;//初位置x0,y0和足够短时间dt通过参数传入

第3步：对于每一步计算：

vx = q1*(x1+R0)/pow(sqrt((x1+R0)*(x1+R0) + y1*y1),3) + q2*(x1-R0)/pow(sqrt((x1-R0)*(x1-R0) + y1*y1),3);//计算水平速度

vy = q1*y1/pow(sqrt((x1+R0)*(x1+R0) + y1*y1),3) + q2*y1/pow(sqrt((x1-R0)*(x1-R0) + y1*y1),3);//计算竖直速度

if((vx*vx + vy*vy) < eps) break;//速度太小提前退出第3步

x2 = x1 + vx*dt;//计算末位置

y2 = y1 + vy*dt;

if(x2 > width/2 || x2 < -width/2 || y2 < -height/2 || y2 > height/2) break;//走出可见区域提前退出第3步

调用pdw.pLine(hDC,x1,y1,x2,y2);[4]绘制一条直线

更新时间、位移和计数器t += dt;s2 = s1;counter++;

r1 = sqrt((x2 + R0)*(x2 + R0) + y2*y2);//计算物体离左边电荷的距离

r2 = sqrt((x2 - R0)*(x2 - R0) + y2*y2);//计算物体离右边电荷的距离

第4步：当r1 > R && r2 > R && counter < 60000即物体没有进入点电荷内部且重复次数没有达到上限时重复进入第3步.

1.4 等势线画法

由于等势线和电场线垂直，只要将式(1)改成

则式(3)、(4)变为

即可.由于等势线关于y轴对称，将初位置选在y轴上(两个点电荷除外),同样使物体正着和倒着各走一次.如果开始向上运动(即v0y*dt>0),只要y>0就一直计算和绘图；如果开始向下运动(即v0y*dt<0),只要y<0就一直计算和绘图.另外要注意不要重复太多或走出可见区域.

2 绘图举例

可见区域统一取-8≤x≤8,-6≤y≤6,为简化计算取k=1，dt=0.01.

(1)q1= 4,q2= 1，如图2.

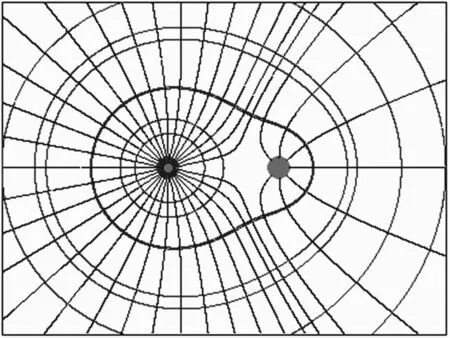
图2 q1∶q2=4∶1

(2)q1= 4,q2= -1，如图3.

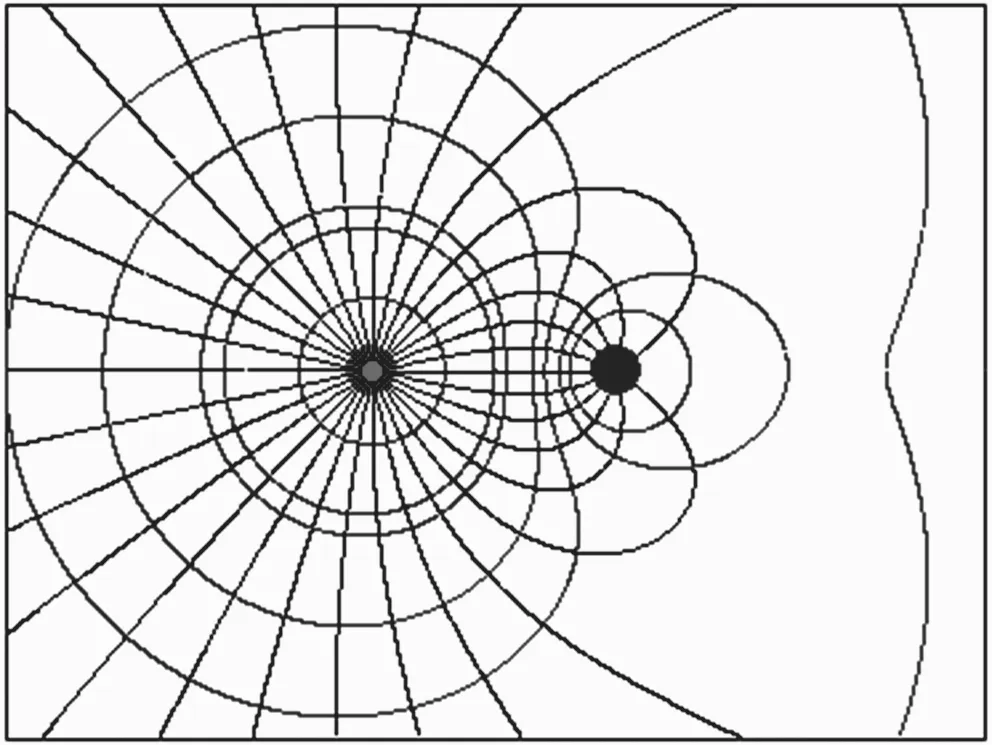
图3 q1∶q2=4∶-1

(3)q1= 2,q2= 2，如图4.

图4 q1∶q2=2∶2

(4)q1= 2,q2= -2，如图5.

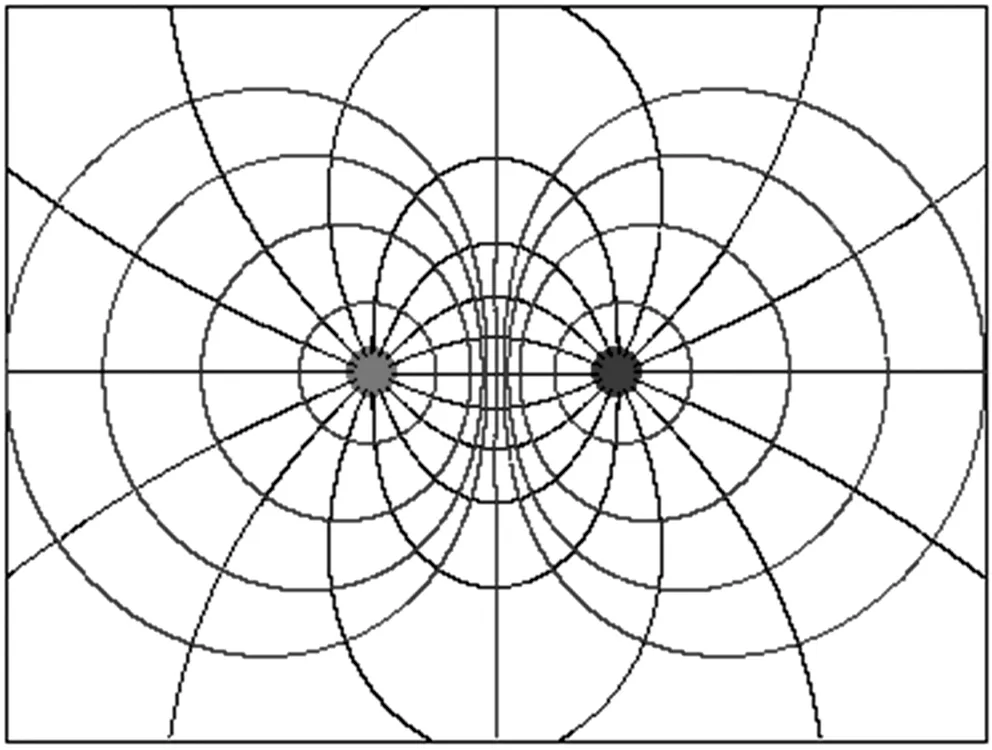
图5 q1∶q2=2∶-2

3 一点讨论

关于电场线和等势线的意义，麦克斯韦在《电磁通论》中指出，“如果我们被要求估计形状给定的一些物体的带电情况，我们就可以从等势面的形状和所给物体形状相近的某一事例开始，然后我们可以利用尝试的办法来改动问题，直到它和所给的情况更近似的对应.这种方法从数学观点看来显然是很不完善的.但这却是我们所具备的唯一方法，而且，如果不许我们选择自己的条件，我们就只能对电分布进行一种近似的计算.因此，看来我们所需要的，就是在我们所能收集和记住的尽可能多的不同事例中关于等势面和电场线之形状的知识[5]”.因为静电平衡后导体表面是一个等势面，通过改变电荷的比例可以得到不同的等势面形状，这样就可以通过多次尝试获得一些问题的近似解.

绘图采用的模拟法不是真实的运动，我们找不到改变运动的合力(加速度)，只是从切线导出的一个等价关系，实际上物体要沿电场线运动是很困难的.当场源为负电荷时，根据“两个方向都走”的策略很容易画出电场线，但当两电荷量不相等时会造成很多重复．文献[2]提出电场线补足的想法，但通过试验笔者却发现当大电荷量增大时，小电荷量收到的电场线条数很快就超过预期值(只是不均匀分布而已)，那么补足的意义何在？因此，除了两电荷量相等之外本文没有考虑接收电场线的一方发出电场线的情况，在这种情况下会对“电荷量和电场线条数成比例”造成一定的破坏，但整体还是符合要求的．

参考文献

1 刘耀康.用计算机绘制点电荷对的电场线.大学物理，2005,(8)59～60

2 石鹏，马凤翔.VC++实现点电荷电场线与电势线的绘制.物理与工程，2013(3)：61～64

3 Harvey Gould,Wolfgang Christian.An Introduction to Computer Simulation Methods:Applications to Physical Systems(3rd ed).北京：高等教育出版社(影印)，2006.369～377

4 曹盼.C/C++在分析小气球运动中的应用.物理教师，2013，(12)68～69

5 (英)麦克斯韦著.电磁通论.戈革译.北京，北京大学出版社，2010.114～116