高温后混凝土冲击破碎能耗及分形特征研究

施劲松,许金余,任韦波,苏灏扬

(1.武汉理工大学土木工程与建筑学院,湖北武汉 430070;2.空军工程大学机场建筑工程系,陕西西安 710038）

高温后混凝土冲击破碎能耗及分形特征研究

施劲松1,许金余2,任韦波2,苏灏扬2

(1.武汉理工大学土木工程与建筑学院,湖北武汉 430070;2.空军工程大学机场建筑工程系,陕西西安 710038）

为研究高温后混凝土在冲击破碎过程中的能量耗散特性及碎块块度分布规律,采用φ100 mm分离式霍普金森压杆装置,对不同温度(常温、200℃、400℃、600℃、800℃)作用后的混凝土进行冲击压缩实验,分析了冲击弹速和温度对试件冲击破碎能耗、破坏形态及碎块分形维数的影响。研究结果表明:同一温度下,耗散能随弹速和应变率的升高不断增大,同一弹速下,耗散能随温度的升高总体呈下降趋势;冲击破坏后混凝土破碎块度分布是一个统计意义上的分形,随弹速及温度的升高,试件破碎程度增大,碎块数目增多、尺寸减小,分形维数增大;耗散能与碎块分形维数的变化在相同温度下具有一定的正相关性。由此可见,不同温度、弹速下混凝土的冲击破碎是外部能量驱动下的分形演化过程。

爆炸力学;混凝土;高温;SHPB;能量耗散;分形维数

Key words:explosion mechanies;concrete;elevated temperature;SHPB;energy dissipation;fractal dimension

0 引言

混凝土是当前国防、人防以及民用建筑工程领域应用最为广泛的一类建筑材料。近年来,随着其使用范围的不断拓展(如核反应堆工程,深地下工程等),以及各类高性能打击武器的快速发展,许多混凝土结构都面临着高温、冲击以及爆炸等极端外部荷载作用的威胁[1],因此,为确保工程结构的使用安全,掌握温度对混凝土动力响应的影响规律,合理进行防护工程的抗打击设计,有必要开展针对混凝土高温冲击动力特性的研究。

文献[2-8]就高温下及高温后混凝土在冲击荷载作用下的应力应变曲线、抗压强度、峰值应变、本构模型及应变率效应等进行了广泛的研究,并得出了许多有益的结论,但同时也可以看出,现有的研究大都集中在一些基本的动力学性能,而针对其在冲击破碎过程中的能量耗散特性以及碎块破损形态、分布规律的研究还相对较少。然而,混凝土高温冲击破坏的本质是混凝土高温下产生的内部损伤裂纹在能量驱动下不断扩展延伸、最终导致材料失稳破坏的能耗过程[9-10],而破坏后碎块的数量、大小以及尺度分布则正是这一过程的宏观表象。通过研究不同温度、加载速率下混凝土耗散能量以及破碎特征的变化,可对其损伤劣化程度,能耗演化机制以及抵抗高温冲击荷载作用的能力做出综合分析评估,避免单纯从强度或变形角度出发的片面性,同时,这对评判武器的打击效果,检验防护工程的防御效能,以及遭受打击后结构破损情况的分析预报也具有重要的参考意义。

因此,本文采用φ100 mm分离式霍普金森压杆(SHPB)实验装置,对常温以及经历200℃、400℃、600℃、800℃高温作用后的混凝土进行冲击压缩实验,并对冲击破碎块度进行筛分统计,分析了冲击弹速和加热温度对试件冲击破碎能耗、破坏形态、碎块分形维数的影响,以及耗散能与分形维数的关系。

1 实验

1.1 原材料与试件

水泥为P.O 42.5R秦岭水泥;粉煤灰为韩城第二发电厂生产的一级粉煤灰;硅灰为霖源微硅粉有限公司生产的微硅粉,平均粒径0.1～0.15 μm,比表面积为15～27 m2/g;粗骨料为泾阳县石灰岩碎石,粒径5～10 mm占15%,10～20 mm占85%;细骨料为灞河中砂,细度模数为2.8;水采用自来水;减水剂为FDN高效减水剂,减水率20%.表1列出了强度等级为C50的混凝土配合比。

表1 C50混凝土配合比Tab.1 Mix proportion of C50 concretekg/m3

将混凝土拌合物搅拌均匀后装入圆柱体试模成型,室温暴露1 d后拆模并放入养护室进行标准养护,28 d后取出进行切割、水磨加工,制得实验所用圆柱形试件,几何尺寸约为φ 98 mm×50 mm.

1.2 实验设备与方法

冲击压缩实验采用φ 100 mm SHPB实验装置(见图1)。该装置利用气压枪驱动子弹,使之与入射杆进行高速同轴撞击并产生入射脉冲,夹置在入射杆与透射杆之间的试件在入射脉冲的加载作用下产生高速变形,同时向入射杆与透射杆分别传播反射脉冲和透射脉冲,这些所需要的脉冲信息由粘贴在压杆上的电阻应变片、超动态应变仪、波形存储器等组成的系统进行测量和记录,再利用“三波法”公式(见(1)式)对数据进行处理,即可得到反映试件材料动态力学性能的相关参数[11]

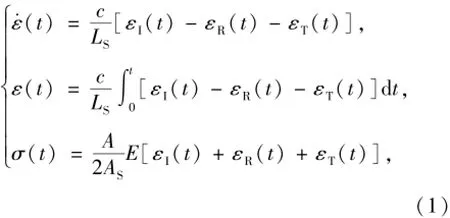
图1 φ 100 mm SHPB实验装置示意图Fig.1 Sketch of φ 100 mm SHPB test apparatus

高温加热设备采用武汉华中电炉设备有限公司生产的RX3-20-12型箱式电阻炉,设计最高温度1 200℃.筛分实验采用孔径为2.5 mm、5 mm、10 mm、16 mm、20 mm、25 mm、31.5 mm、40 mm、50 mm的标准筛,并利用电子称测得每级筛上滞留的碎块质量。

实验共设4个加热温度等级(200℃、400℃、600℃和800℃),并以常温(25℃)作为对照组,冷却方式采用喷水冷却。这是因为冷却方式对高温后混凝土残余力学性能影响显著[12],混凝土在较大温度梯度和热应力的作用下较自然冷却时会产生更为严重的损伤,实际的火灾现场常采用喷水灭火,因此将高温加热后进行喷水冷却处理作为研究工况更具实际意义。

实验开始时,先将试件放入电阻箱,按10℃/min的加热速率加热至指定温度,并在箱内恒温2 h.待加热完毕后将试件立即取出进行喷水冷却(喷淋30 min),并在室内条件下静置24 h.然后,对每个温度等级下的试件共进行5组不同弹速(5.5 m/s、6.5 m/s、7.5 m/s、8.5 m/s、9.5 m/s)的冲击实验,每个弹速下至少进行3次重复实验,弹速通过调节气压进行控制。同时,为满足SHPB实验的两个基本假定[13],确保实验结果有效可靠,采用厚度为1 mm,直径分别为30 mm、35 mm、40 mm、45 mm、50 mm的铝片作为波形整形器。最后,收集冲击实验后的试件碎块并进行筛分、称量。

2 冲击破碎能耗分析

2.1 冲击破碎过程中的能量计算

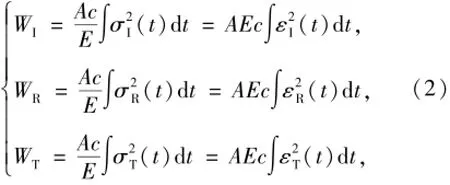
SHPB实验中,从开始加载到卸载过程中入射波、反射波和透射波所携带的能量WI、WR和WT可分别表示为式中:σI(t)、σR(t)、σT(t)分别为入射、反射和透射应力波。由于实验过程中在试件两个端面上均匀涂抹了用润滑油和石墨配置的润滑剂,因此可以不考虑试件与压杆间摩擦力所消耗的能量。根据能量守恒定律,试件在冲击破碎过程所吸收的能量WA可由(3)式进行计算

WA主要由三部分构成,即用于裂纹萌生、扩展,促使试件失稳破坏的耗散能Wde,试件碎块的动能Wv以及通过热能、声能、电磁能等其他形式耗散的能量Wo.根据文献[14]的研究成果可知,在弹速不是特别高的情况下,Wv与Wo在总吸收能WA中仅占很小一部分,可以忽略,因此可以近似地认为WA=Wde.

2.2 弹速及温度对耗散能的影响

高温后混凝土冲击破坏过程中的能耗特性主要取决于两方面因素,即作用于试件的外部能量以及试件内部的初始损伤状态。前者主要受加载速率(弹速)的影响,是导致试件损伤破坏的直接原因,裂纹的萌生、繁衍、扩展和贯穿,每一个阶段都要从外部吸收能量,是不可逆的能耗过程;后者主要受作用温度的影响,不同温度下试件内部的微观损伤程度不同,致使其抵抗应力波作用的能力发生改变,进而影响试件的宏观吸能特性。

图2和图3分别为不同温度下耗散能Wde随弹速v和平均应变率ε·的变化关系,图4和图5分别为不同弹速下耗散能Wde随温度θ的变化关系以及不同温度下残余能耗比Ke的变化规律(Ke为弹速相同时各温度等级下的耗散能与常温时耗散能的比值)。

从图2～图5可以看出,在本文研究范围内:1)同一温度下,随着弹速和应变率的升高,耗散能不断增大,加载速率效应显著,以加热温度600℃的试件为例,在5.5～9.5 m/s的弹速范围内,平均应变率从70.48 s-1增至134.49 s-1,耗散能从127.2 J增至391.2 J,增幅达到207.6%.2)同一弹速下,随着温度的升高,耗散能与残余能耗比总体上均呈下降趋势,但在不同的温度及弹速区间,其变化趋势又有所差异,显然试件耗散能的变化受温度和弹速两方面因素的共同影响。具体表现为:当加热温度较低时(200℃和400℃),耗散能在低速段(5.5～7.5 m/s)较常温有所减小,而在高速段(8.5～9.5 m/s),接近甚至超过常温时的水平。例如对于加热温度200℃的试件,其在图2和图5中的曲线同常温时的曲线出现了交汇,相应的残余能耗比在5.5～9.5 m/s的弹速范围内分别为0.79、0.72、0.73、1.07和1.17,而当加热温度较高时(600℃和800℃),不同弹速下的耗散能较常温均出现明显下降,但随着弹速的增大,其降低幅度逐渐减小,残余能耗比有所上升。

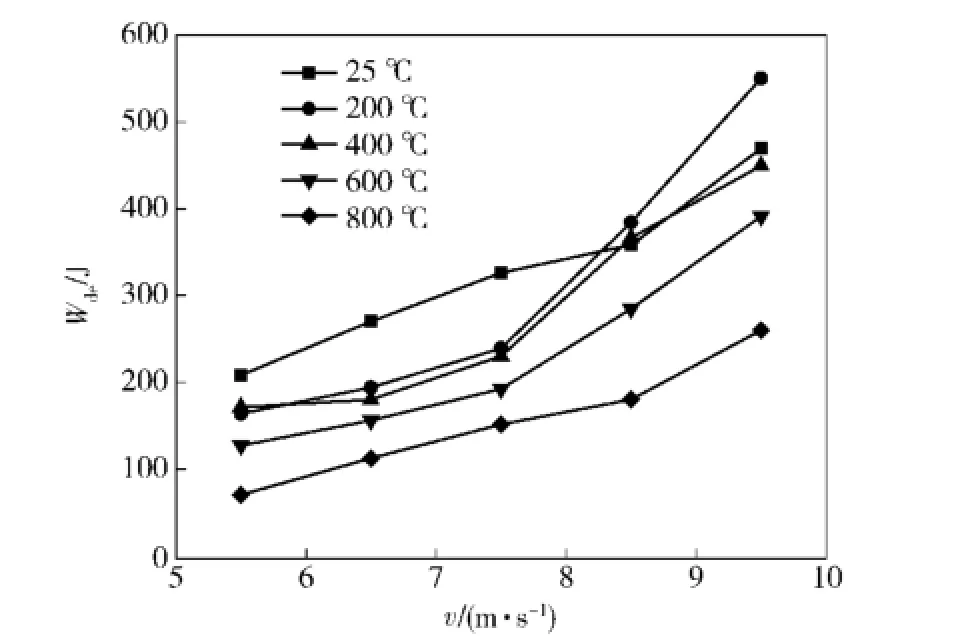
图2 不同温度下耗散能与弹速的关系Fig.2 Relationship between dissipated energy andimpact velocity at different temperatures

图3 不同温度下耗散能与应变率的关系Fig.3 Relationship between dissipated energy and strain rate at different temperatures

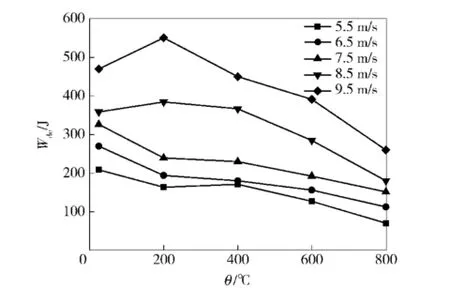
图4 不同弹速下耗散能与温度的关系Fig.4 Relationship between dissipated energy and temperature at different impact velocities

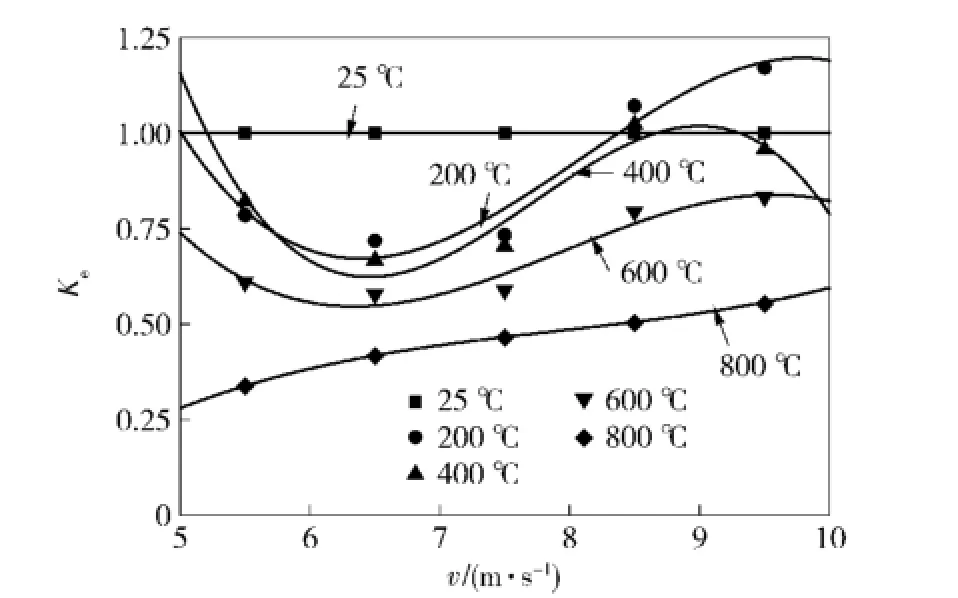
图5 不同温度下Ke与弹速的关系Fig.5 Relationship between Keand impact velocity at different temperatures

上述混凝土冲击破碎能耗随弹速及温度的变化原因可从以下两方面进行解释:1)在冲击荷载作用下,加载速率的提高导致荷载作用时间变短,试件应变率增大,裂纹来不及沿着最薄弱界面扩展贯通,而是在各自区域同时萌生大量新的微裂缝以抵消外部荷载能量,而裂纹产生所消耗的能量远比裂纹扩展所消耗的能量要高,因此弹速越大,产生的裂纹数目就越多,耗散能也就越大。2)经历不同温度作用后,混凝土内部组织结构及物质成分的改变使其能耗特性发生相应变化。200℃时,试件耗散能在低弹速段较常温出现下降的主要原因并非高温损伤所致,而是由于此时加热温度较低,温度的损伤软化效应较小,导致混凝土性能变化对温度的敏感性较弱,加之自由水分的蒸发使得试件收缩密实以及部分水泥颗粒的二次水化作用[15],致使高温及喷水冷却对材料造成的负面影响得以弥补,试件在外部冲击荷载作用下的损伤演化过程减缓,因而在低弹速打击下其破坏程度较小,耗散能较常温下有所减小,而随着弹速的提高,试件破损程度增大。但由于试件整体失稳破坏过程的延缓,导致耗散能持续累积增大,甚至高于常温水平。此后,随着温度的升高,试件整体性、密实性遭到破坏,原生裂纹增多,初始劣化程度增大。当冲击荷载作用时,内部裂纹加速扩展,试件急剧破坏,使得耗散能不断减小。

3 冲击破碎块度的分形特征

3.1 冲击破碎形态及块度分布

高温后混凝土冲击失稳破坏的过程,就是其内部细观损伤裂纹在外荷作用下不断孕育、发展、聚集,最终引发宏观破碎的过程,其破坏模式反映着混凝土的受力能耗状态及损伤演化的程度,不同的冲击速度及加热温度必然导致其破碎形态发生改变。

图6和图7分别给出了不同弹速下试件的典型破坏形态以及破碎块度分布的双对数坐标曲线(由于篇幅所限,仅选取常温及800℃为代表温度),其中,mr为粒径小于r的碎块累计质量;mT为碎块总质量。从图6和图7可以看出:随着弹速的提高,碎块数目增多,尺寸减小且趋于均匀,块度分布曲线逐渐平缓,破碎程度不断增大。此外,当温度较低时,试件破碎形态多为条状、块状的大、中粒径碎块(10～40 mm),而当温度较高时,碎块颜色变白,多为均匀细小的颗粒粉末(10 mm以下)。这是因为,低温时,试件内部裂纹较少,且在动荷作用下直接在原位扩展贯穿,导致试件破碎程度较小且呈劈裂破坏,而随着温度的升高,轴向及横向裂纹分布密度增大,在动荷作用下迅速失稳贯通,将试件“切割”成细粒状,导致试件破碎程度加剧且呈压碎破坏。

图6 不同弹速下混凝土的破坏形态Fig.6 Failure modes of concrete at different impact velocities

图7 In[mr/mT]-Inr曲线Fig.7 In[mr/mT]-Inr curves

3.2 分形维数的计算

由文献[16]可知,高温后混凝土冲击破碎块度符合G-G-S分布,根据质量-频率关系,可知其分布方程为

式中:r为碎块粒径;rm为碎块的最大尺寸;b为碎块分布参数,即In[mr/mT]-Inr曲线的斜率。

再根据分形维数的定义,即N=r-D(N为粒径大于r的碎块个数,D为碎块的分形维数),同时考虑到碎块数量增量与碎块质量增量的关系,即dm∝r3dN,便可由质量-粒度[17]方法计算得到碎块的分形维数D,即

图7中的数据点在双对数坐标下总体上具有较好的线性相关性,表明冲击破坏后混凝土碎块的分布具有分形特征。这是因为,混凝土内部细观裂纹、孔隙在不同尺度下具有自相似性,而破碎过程与碎块形状又是裂隙扩展的直接结果,因而导致碎块尺度分布具有幂律特征,是一个统计意义上的分形。分维值越大,表示碎块数目越多,尺寸越小,试件破碎程度越高。此外,虽然在温度较高时(如800℃)因碎屑粒径主要集中在细粒端,导致图中拟合曲线与数据点具有一定偏差,但其相关系数R仍在0.9以上,而且本实验在不同工况下均采用同一系列的筛分孔径(即尺度相同),故所得分维值不失可比性。

3.3 弹速与温度对分形维数的影响

图8和图9分别为不同温度下分形维数D以及速度分形维数比IFDv随弹速v的变化关系(IFDv为温度相同时各弹速下分形维数与最低弹速分形维数的比值),图10和图11分别为不同弹速下分形维数D以及温度分形维数比IFDθ随温度θ的变化关系(IFDθ为弹速相同时各温度等级分形维数与常温时分形维数的比值)。

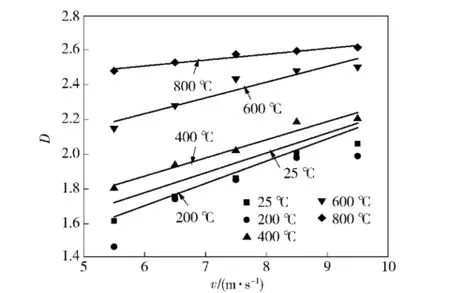
图8 不同温度下分形维数与弹速的关系Fig.8 Relationship between fractal dimension and impact velocity at different temperatures

从图8～图11可以看出:1)同一温度下,分形维数随弹速的提高而不断增大,相同弹速变化范围内,分形维数值的增幅在200℃时达到最大,而后随温度的升高逐渐下降,在5.5～9.5 m/s的弹速范围内,各级温度下的分形维数值分别处于1.71～2.15,1.56～2.08,1.80～2.20,2.15～2.50,2.48～2.61.2)同一弹速下,分形维数随温度的升高总体呈上升趋势,但在200℃时,分形维数值接近或低于常温水平,相同温度变化范围内,分形维数值的增幅随弹速的提高而减小,在25～800℃的温度范围内,各级弹速下的分形维数值分别处于1.71～2.48, 1.85～2.53,1.95～2.57,2.09～2.59,2.15～2.61.对不同温度下的弹速及分形维数按D=c+dv进行回归分析(c和d为拟合系数),可得图8中的拟合直线,具体拟合系数见表2.

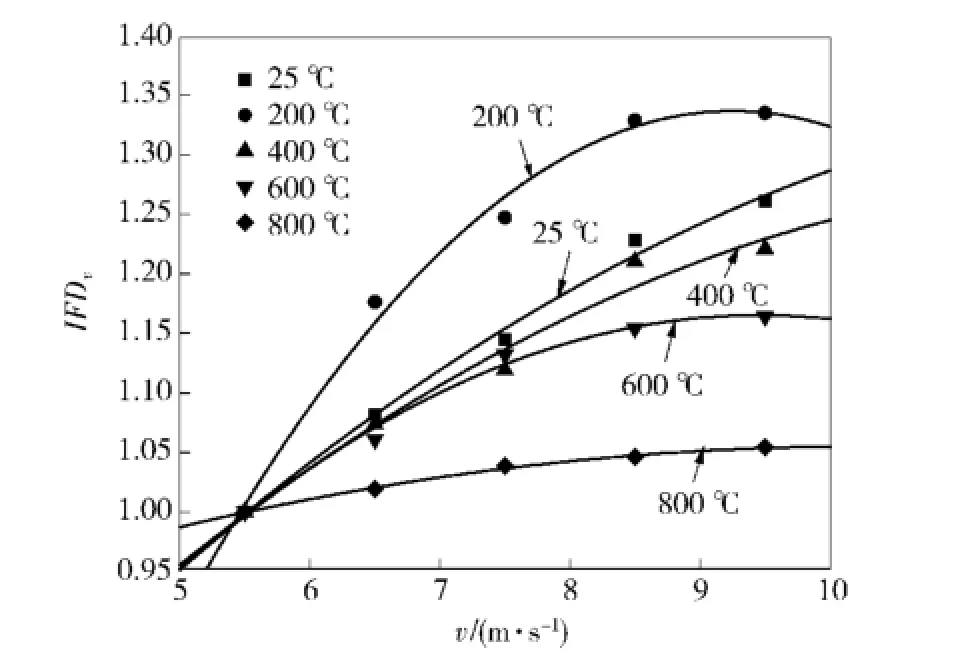
图9 不同温度下IFDv与弹速的关系Fig.9 Relationship between IFDvand impactvelocity at different temperatures

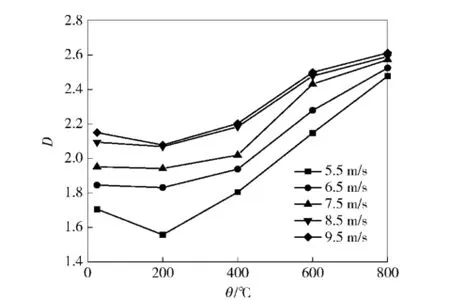
图10 不同弹速下分形维数与温度的关系Fig.10 Relationship between fractal dimension and temperature at different impact velocities

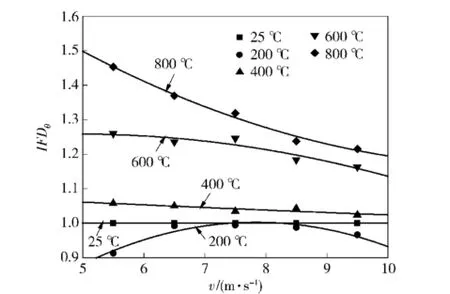
图11 不同温度下IFDθ与弹速的关系Fig.11 Relationship between IFDθand impact velocity at different temperatures

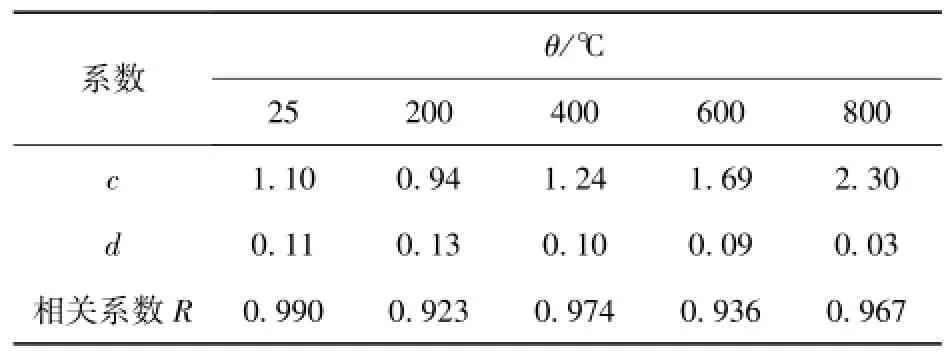
表2 不同温度下弹速与分形维数线性关系拟合表Tab.2 Linear relationship between fractal dimensionand impact velocity at different temperatures

通过上述分析可以看出,弹速及温度的升高均使碎块的分形维数得以增大。这是因为,弹速越高,试件破碎的就越彻底,而温度的升高使得试件内部各相界面处粘聚力减小,基体承载力降低,微裂纹增多,促使试件在冲击荷载作用下进一步破坏,但在200℃时,由2.2节中的分析可知,此时试件性能对温度变化并不敏感,且在外荷载作用下的损伤演化速率有所降低,故在相同弹速打击下试件破碎程度及分形维数值较小。利用碎块分形维数对试件的破碎程度进行表征具有一定的合理性。

3.4 分形维数与耗散能量的关系

对外部冲击能量耗散程度的不同以及冲击破碎形态的改变,是不同温度、弹速下混凝土冲击破碎特性的内因与表象,因此,冲击破碎过程中的耗散能与破碎块度的分形维数值具有内在的本质联系[18]。图12给出了不同温度下分形维数与耗散能的关系,从中可以看出:在同一温度下,耗散能均随着分形维数的增大而不断增大,二者具有一定的正相关性;随着温度的升高,同一分形维数值对应的耗散能不断减小,但在200℃时,随着分形维数的增大,试件的耗散能逐渐接近并高于常温值,当温度超过600℃时,相同耗散能下的碎块分形维数值明显增大,说明温度的损伤软化效应显著。

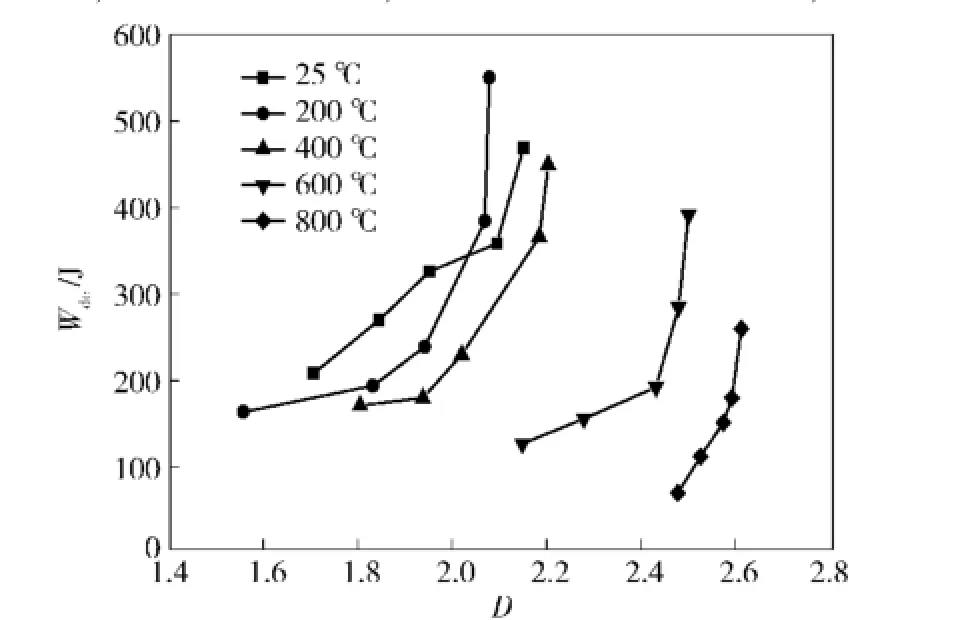
图12 不同温度下分形维数与耗散能的关系Fig.12 Relationship between fractal dimension and dissipated energy at different temperatures

4 结论

1)高温后混凝土冲击破碎过程中的能耗特性主要受弹速及加热温度的影响。同一温度下,耗散能随弹速和应变率的升高不断增大,同一弹速下,随着温度的升高,耗散能总体呈下降趋势。

2)冲击破坏后混凝土破碎块度的分布具有自相似性,是一个统计意义上的分形。随着弹速及温度等级的升高,试件破碎程度增大,碎块数目增多、尺寸减小,破碎块度的分形维数逐渐增大。利用分形维数对试件的破碎程度进行表征具有一定的合理性。

3)200℃时,混凝土性能变化对温度的敏感性较弱,试件在外部冲击荷载作用下的损伤演化过程减缓,造成此时试件耗散能在低速段较常温有所减小,在高速段接近甚至超过常温水平,且该温度下试件碎块的分形维数均接近或低于常温水平。

4)混凝土冲击破碎过程中的耗散能与碎块分形维数的改变具有内在本质联系。在同一温度下,耗散能随分形维数的增大不断增大;随着温度的升高,同一分形维数对应的耗散能不断减小,同一耗散能对应的分形维数明显增大。

References)

[1] 贾彬.混凝土高温静动力学特性研究[D].重庆:重庆大学, 2011.

JIA Bin.Static and dynamic mechanical behavior of concrete at elevated temperature[D].Chongqing:Chongqing University,2011. (in Chinese)

[2] 许金余,刘健,李志武,等.高温中与高温后混凝土的冲击力学特性[J].建筑材料学报,2013,16(1):1-5.

XU Jin-yu,LIU Jian,LI Zhi-wu,et al.Impact mechanical properties of concrete at and after exposure to high temperature[J]. Journal of Building Materials,2013,16(1):1-5.(in Chinese)

[3] 李志武,许金余,白二雷,等.高温后混凝土SHPB试验研究[J].振动与冲击,2012,31(8):143-146.

LI Zhi-wu,XU Jin-yu,BAI Er-lei,et al.SHPB test for post-hightemperature concrete[J].Journal of Vibration and Shock,2012, 31(8):143-146.(in Chinese)

[4] 何远明,霍静思,陈柏生,等.高温下混凝土SHPB动态力学性能试验研究[J].工程力学,2012,29(9):200-207.

HE Yuan-ming,HUO Jing-si,CHEN Bai-sheng,et al.Impact tests on dynamic behavior of concrete at elevated temperatures[J].Engineering Mechanics,2012,29(9):200-207.(in Chinese)

[5] 贾彬,陶俊林,李正良,等.高温混凝土动态力学性能的SHPB试验研究[J].兵工学报,2009,30(增刊2):208-212.

JIA Bin,TAO Jun-lin,LI Zheng-liang,et al.SHPB test for dynamic mechanical performances of concrete at high temperatures[J]. Acta Armamentarii,2009,30(S2):208-212.(in Chinese)

[6] 范飞林,许金余,李志武,等.高温下混凝土动态力学特性试验[J].材料热处理学报,2012,33(3):22-26.

FAN Fei-lin,XU Jin-yu,LI Zhi-wu,et al.Experiment for dynamic mechanical properties of concrete at high temperatures[J].Transactions of Materials and Heat Treatment,2012,33(3):22-26. (in Chinese)

[7] 陶俊林,秦李波,李奎,等.混凝土高温动态压缩力学性能实验[J].爆炸与冲击,2011,31(1):101-106.

TAO Jun-lin,QIN Li-bo,LI Kui,et al.Experimental investigation on dynamic compression mechanical performance of concrete at high temperature[J].Explosion and Shock Waves,2011,31(1): 101-106.(in Chinese)

[8] Li Z W,Xu J Y,Bai E L.Static and dynamic mechanical properties of concrete after high temperature exposure[J].Materials Science and Engineering:A,2012,544:27-32.

[9] 谢和平,彭瑞东,鞠杨,等.岩石破坏的能量分析初探[J].岩石力学与工程学报,2005,24(15):2604-2608.

XIE He-ping,PENG Rui-dong,JU Yang,et al.On energy analysis of rock failure[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(15):2604-2608.(in Chinese)

[10] 谢和平,彭瑞东,鞠杨.岩石变形破坏过程中的能量耗散分析[J].岩石力学与工程学报,2004,23(21):3565-3570.

XIE He-ping,PENG Rui-dong,JU Yang.Energy dissipation of rock deformation and fracture[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(21):3565-3570.(in Chinese)

[11] 王礼立.应力波基础[M].北京:国防工业出版社,2005.

WANG Li-li.Foundation of stress waves[M].Beijing:National Defense Industry Press,2005.(in Chinese)

[12] Nassif A Y.Post firing stress-strain hysteresis of concrete subjected to various heating and cooling regimes[J].Fire and Materials,2002,26:103-109.

[13] 李为民,许金余.大直径分离式Hopkinson压杆试验中的波形整形技术研究[J].兵工学报,2009,30(3):350-355.

LI Wei-min,XU Jin-yu.Pulse shaping techniques for largediameter split Hopkinson pressure bar test[J].Acta Armamentarii,2009,30(3):350-355.(in Chinese)

[14] Zhang Z X,Kou S Q,Jiang L G,et al.Effects of loading rate on rock fracture:fracture characteristics and energy partitioning[J]. Journal of Rock Mechanics and Mining Sciences,2000,37(5): 745-762.

[15] Mehmet B K.Effect of cooling regimes on compressive strength of concrete with lightweight aggregate exposed to high temperature [J].Construction and Building Materials,2013,41:21-25.

[16] 杨军,金乾坤,黄凤雷.岩石爆破理论模型和数值计算[M].北京:科学出版社,1999.

YANG Jun,JIN Qian-kun,HUANG Feng-lei.Rock explosion theory model and numerical calculation[M].Beijing:Science Press,1999.(in Chinese)

[17] 何满潮,杨国兴,苗金丽,等.岩爆实验碎屑分类及其研究方法[J].岩石力学与工程学报,2009,28(8):1522-1528.

HE Man-chao,YANG Guo-xing,MIAO Jin-li,et al.Classification and research methods of rockburst experimental fragments[J]. Chinese Journal of Rock Mechanics and Engineering,2009, 28(8):1522-1528.(in Chinese)

[18] 黎立云,徐志强,谢和平,等.不同冲击速度下岩石破坏能量规律的实验研究[J].煤炭学报,2011,36(12):2008-2011.

LI Li-yun,XU Zhi-qiang,XIE He-ping,et al.Failure experimental study on energy laws of rock under differential dynamic impact velocities[J].Journal of China Coal Society,2011,36(12): 2008-2011.(in Chinese)

Research on Energy Dissipation and Fractal Characteristics of Concrete after Exposure to Elevated Temperatures under Impact Loading

SHI Jin-song1,XU Jin-yu2,REN Wei-bo2,SU Hao-yang2
(1.School of Civil Engineering and Architecture,Wuhan University of Technology,Wuhan 430070,Hubei,China;
2.Department of Airfield and Building Engineering,Air Force Engineering University,Xi'an 710038,Shaanxi,China)

The energy dissipation capacities and fragments distribution of concrete exposed to high temperature under impact loading are studied.Dynamic compressive tests of concrete at room temperature and after exposure to elevated temperatures ranging from 200 to 800℃are conducted by using a split Hopkinson pressure bar with 100 mm in diameter.The effects of high temperature and impact velocity on dissipated energy,failure mode and fractal dimension of fragments are analyzed.The results indicate that the dissipated energy grows with the increase in impact velocity and strain rate at the same temperature; and at fixed impact velocity,the dissipated energy decreases with the increase in the exposure temperature.The fragment-size distribution of concrete fragments statistically has fractal property subjected to impact loading.An increase in temperature and impact velocity results in a greater crushing degree and a larger fractal dimension value.There is a positive correlation between dissipated energy and fractal dimension at the same temperature.As a result,the impact crushing of concrete at various temperatures and impact velocities is a fractal evolution process driven by external energy.

O 347;TU528.01

:A

1000-1093(2014)05-0703-08

10.3969/j.issn.1000-1093.2014.05.019

2013-06-18

国家自然科学基金项目(51078350、51208507)

施劲松(1971—),男,工程师,博士研究生。E-mail:sjs66688@163.com;许金余(1963—),男,教授,博士生导师。E-mail:jyx369@yeah.net