变后掠变展长飞行器动力学建模与动态响应分析
2014-06-27杨贯通唐胜景赵林东郭杰
杨贯通,唐胜景,赵林东,郭杰
(北京理工大学飞行器动力学与控制教育部重点实验室,北京 100081)
变后掠变展长飞行器动力学建模与动态响应分析
杨贯通,唐胜景,赵林东,郭杰
(北京理工大学飞行器动力学与控制教育部重点实验室,北京 100081)
飞行器机翼后掠角和展长动态变化时,气动力、转动惯量、压力中心和质心等关键参数都发生剧烈变化。基于Newton-Euler方法建立了包含5个刚体的变后掠变展长飞行器的动力学模型,推导了由于变形所产生的附加气动力和气动力矩。在纵向上解耦简化了动力学方程,基于准定常气动力模型,分析了不同变形形式和变形速度下的纵向动态响应。研究结果表明,后掠角和展长的变化对动力学特性影响较大,但不同的变化速度对结果影响不大。通过合适的变形方式和变形速度的结合可以弱化变形过程中的动力学参数波动,减小控制系统的负担。
应用力学;无人机;变后掠变展长;动力学建模;动态响应
0 引言
传统的飞行器最优功能和性能往往只是体现在某些特定的飞行任务和飞行状态上。变气动外形飞行器能够满足大空域和大速域的飞行要求,可以在多种飞行状态下保持最优飞行,使得该飞行器能够执行常规飞行器所不能完成的任务[1-2]。William提炼出了在变形飞机概念设计阶段最为关键的6个变量:推重比、翼载、翼厚度与弦长比、翼根梢比、翼后掠角、翼展弦比[3]。变后掠变展长无人飞行器综合了翼后掠角和翼展弦比二种大尺度变形方式,是可变外形飞行器的一个重要研究方向。
对于变外形无人飞行器,气动外形改变是一个关键的飞行过程,在变形过程中飞行器的质量特性、气动特性都发生显著变化,需要对该过程进行详细的建模和分析,把握关键参数的变化规律,为控制系统设计提供依据。在变后掠变展长飞行器方面,已有一些气动特性研究成果[4],动力学研究还比较少见;在变外形飞行器动力学建模和动态响应分析方面,已有对变后掠飞机以及折叠飞机等有意义的研究[5-8]。
1 变后掠变展长无人飞行器
在某原型无人机(如图1所示)的基础上,设计了后掠角和展长均可变的无人飞行器。特殊的气动外形使其能够实现侦察和打击一机融合,实现自主空中侦察、战场监视、战场决策和打击等任务。其3种典型的飞行状态如图2所示。

图1 作为基准模型的小型无人机Fig.1 The referential UAV
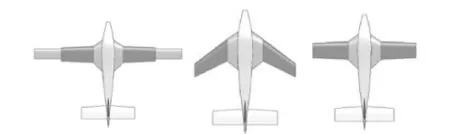
图2 3种典型飞行状态Fig.2 Typical flight states
2 多体动力学建模
变外形飞行器是一个空间运动的多体系统,传统的6自由度飞行器动力学模型不再适用,需要基于多体动力学建模方法重新推导动力学方程。
2.1 坐标系的建立
变外形飞行器一般有3个特征点可以选作坐标系原点:总质心、机体质心和飞机头部。由于总质心是变化的,坐标系也会在飞行器上运动,增加了建模难度;飞机头部作为原点,会直接增加力矩项,使建模过程变得复杂。而机体坐标系原点选在机身质心上,建模最为直观和简洁。在变形之前,即0°后掠角时,整个无人机的总质心与机身的质心重合。变形时,飞机质心位置和坐标系原点不再重合,并且随后掠角和展长的变化在空间运动,将产生附加动力和力矩。为方便研究,将可变后掠翼和伸缩翼的质量集中于其质心。
如图3所示,OXYZ为机体坐标系,Oxyz为地面坐标系。地面坐标系到机体坐标系的矢径为ro,gi点为单个可活动机翼的质心。机体坐标系原点到gi点的矢径为Si,地面坐标系到gi点的矢径为rgi.用下标f表示机身,下标1表示左后掠翼,2表示右后掠翼;3表示左伸缩翼,4表示右伸缩翼。对机身和机翼易得速度矢量(1)式。
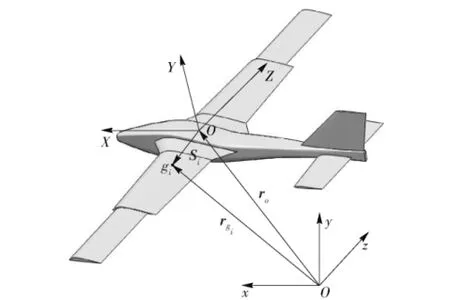
图3 坐标系示意图Fig.3 Coordinate system
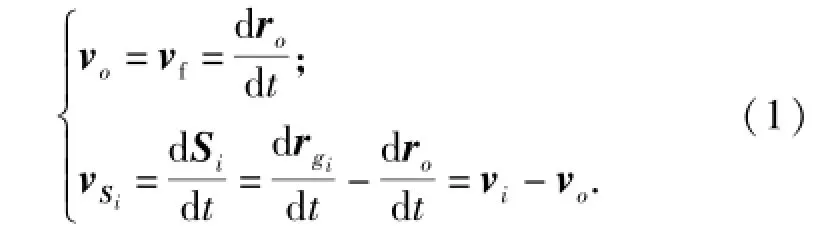
2.2 平动动力学
对机身、4片机翼分别列写动量定理
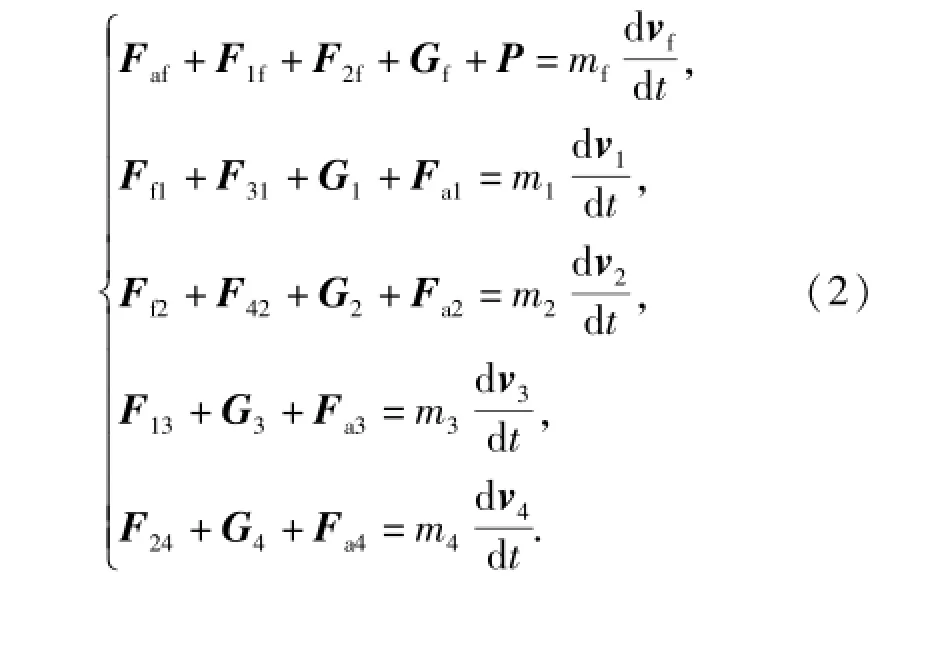
式中:Faf表示空气动力对机身的作用力;F1f表示左侧后掠翼对机身的作用力;G1代表左侧后掠翼的重力;P代表发动机推力;其他类推。整理(2)式并根据(1)式得到
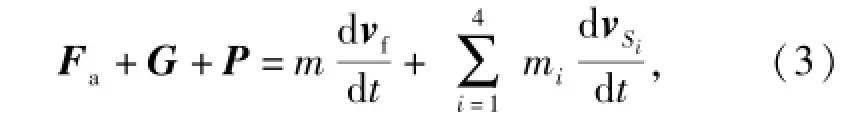
式中:m是总质量;G是总重力。可以发现与传统飞行器6自由度方程相比,该方程多了等式右侧机翼运动附加力。进一步推导得到
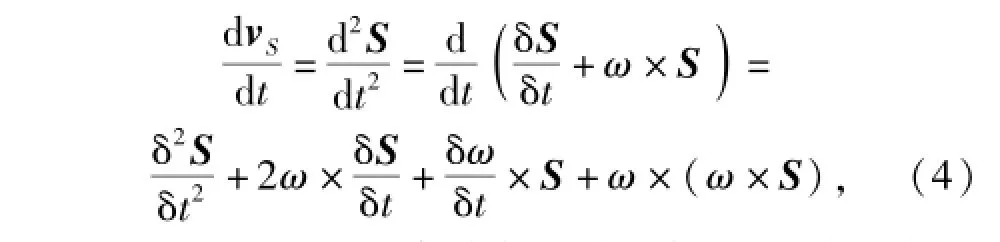
式中:ω为飞行器的旋转角速度,将ω连同S表示成机体坐标系内的向量形式,带入(4)式可得到附加力。需要注意,该力是表示在机体坐标系下的。
2.3 转动动力学
对第i块机翼,根据动量矩定义[9]知
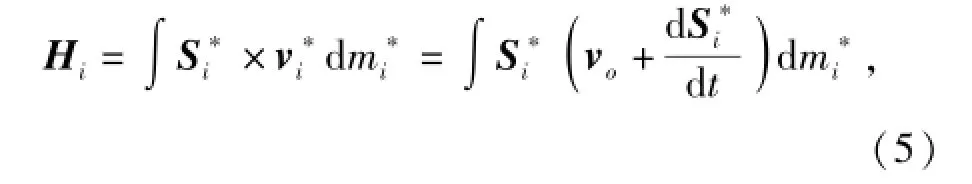
式中:上标*表示机翼上的单位微元。
直接对两侧求导得到

整理之后得
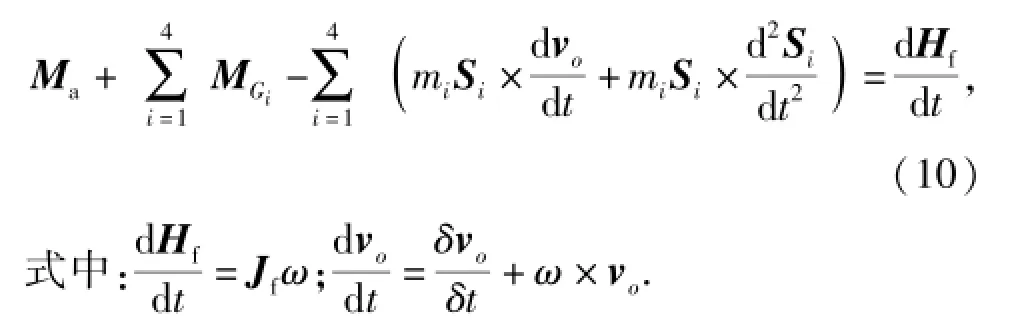
(10)式等式左侧除Ma为飞行器受到的气动力矩,其余均是附加力矩项。
3 纵向动力学模型
3.1 纵向动力学模型
两侧对称变形时,由于左右两侧具有运动的一致性和对称性,易得
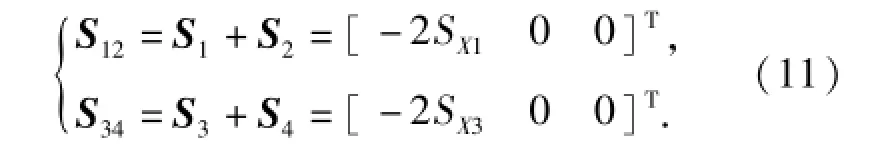
此时附加力和附加力矩可以按后掠翼和伸缩翼分为2组。根据(11)式对力和力矩方程进行简化,得到由后掠翼引起的机体坐标系OX轴、OY轴上的附加力
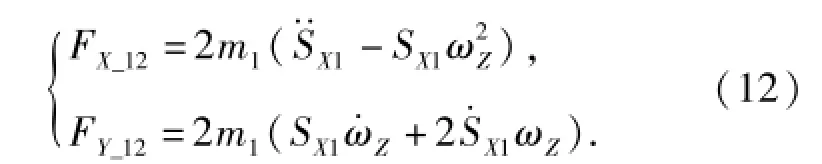
由后掠翼引起的关于Z轴的附加力矩为
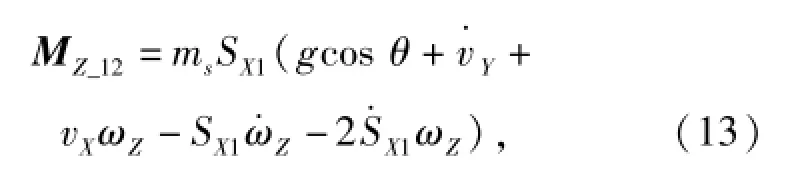
vX、vY为速度在机体坐标系上的投影。最终得到变后掠变展长飞行器纵向动力学方程
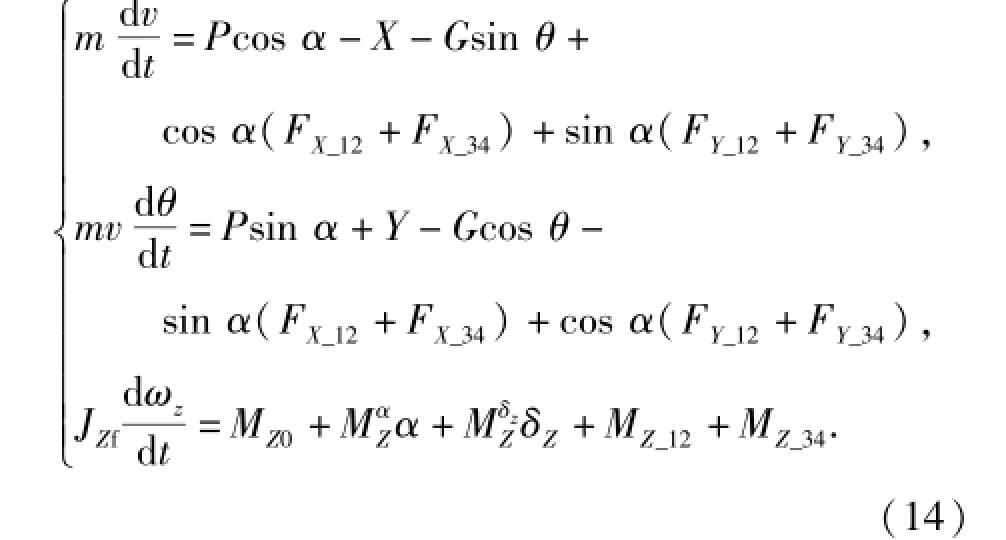
3.2 几何关系
飞行器的几何关系如图4所示。
由图4易知以下几何关系
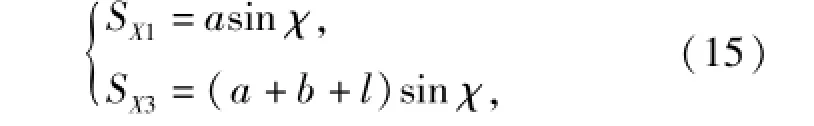
式中:a、b是与外形有关的定值;后掠角χ和伸缩展长l均是控制量。(12)式中所需的对时间一阶和二阶导数均易导出。

图4 几何关系示意图Fig.4 The geometric relationship
4 动态响应仿真与分析
对变形过程进行动力学仿真,变形之前飞行器处于定直平飞状态,主要参数列于表1.变形过程中采用准定常气动力计算。
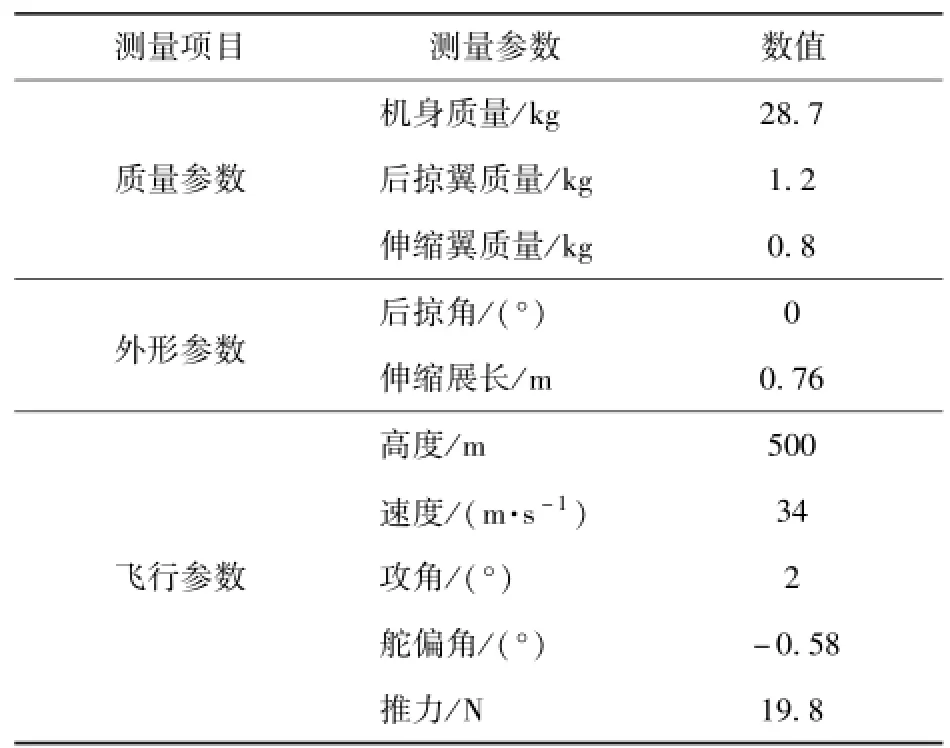
表1 平飞主要参数Tab.1 Parameters of straight flight
4.1 不同后掠角变化时的动态响应
保持飞行器的展长不变,后掠角分别以4°/s、8°/s、10°/s的速度变化,得到的后掠角、高度、速度、攻角和俯仰角速度等运动参数的动力学响应如图5所示。
从图5可以看出,由于后掠角的增加,导致气动焦点、压心均剧烈后移,使得气动力产生的低头力矩迅速增加,滚转角速度增加,俯仰角减小,但弹道倾角变化相对缓慢,进而导致飞行器的攻角迅速降低。随着后掠角的增加,展弦比减小,升力系数显著降低,飞行器开始迅速掉高。注意到附加力矩是抬头力矩,可知变形过程实际是气动特性与质量特性的博弈,但气动参数的变化更加剧烈,因此飞行器低头趋势占据了主导,同时需注意在设计时考虑放宽静稳定性。从图中还可以看出,后掠角变化速率快时,使得各参数的变化趋势提前发生,但总体影响不显著。
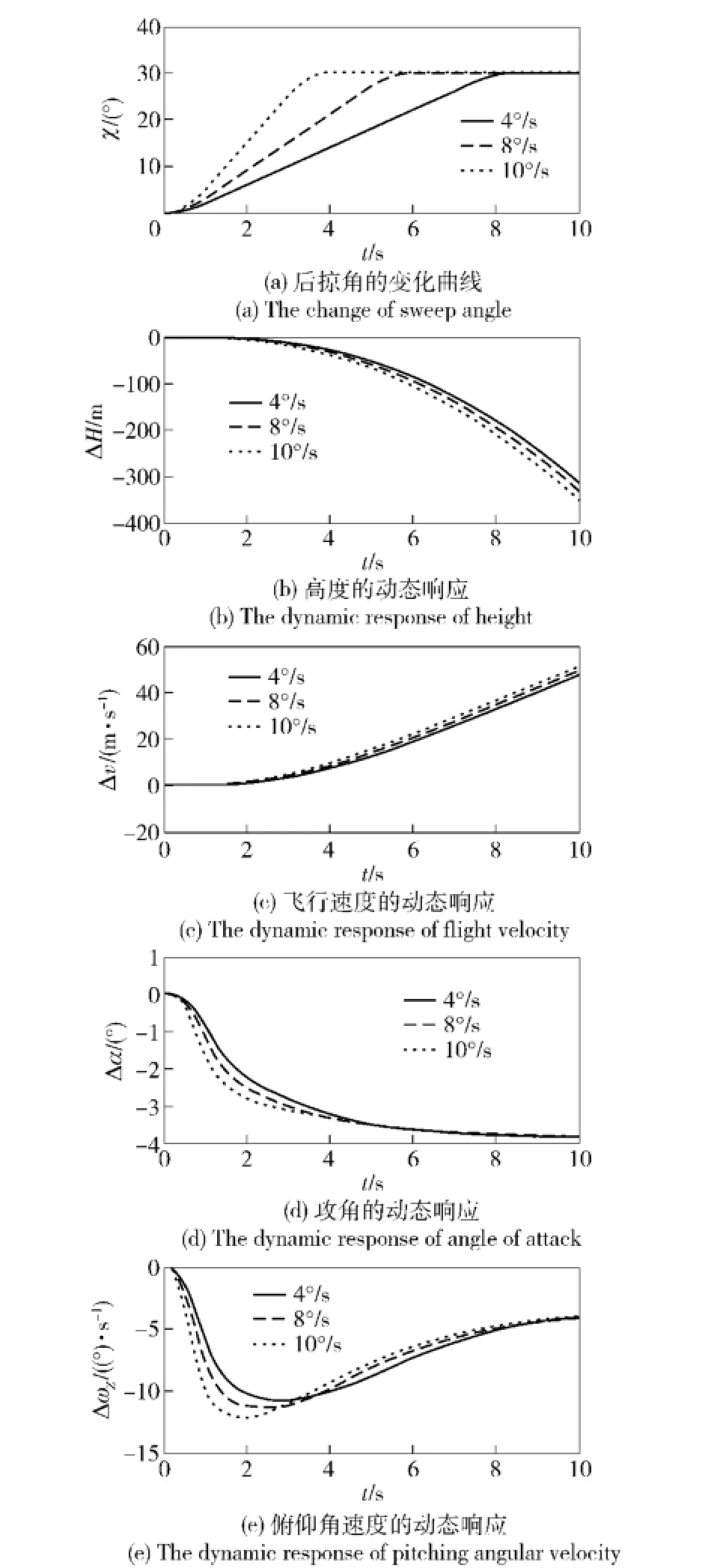
图5 不同后掠角变化速率下的动态响应Fig.5 The dynamicre sponses at different morphingspeeds of sweep angle
4.2 不同展长变化时的动态响应
保持飞行器的后掠角不变,展长分别以0.2 m/s、0.3 m/s、0.5 m/s的速度变化,得到的伸缩翼展长、高度、速度、攻角和俯仰角速度等运动参数的动力学响应如图6所示。
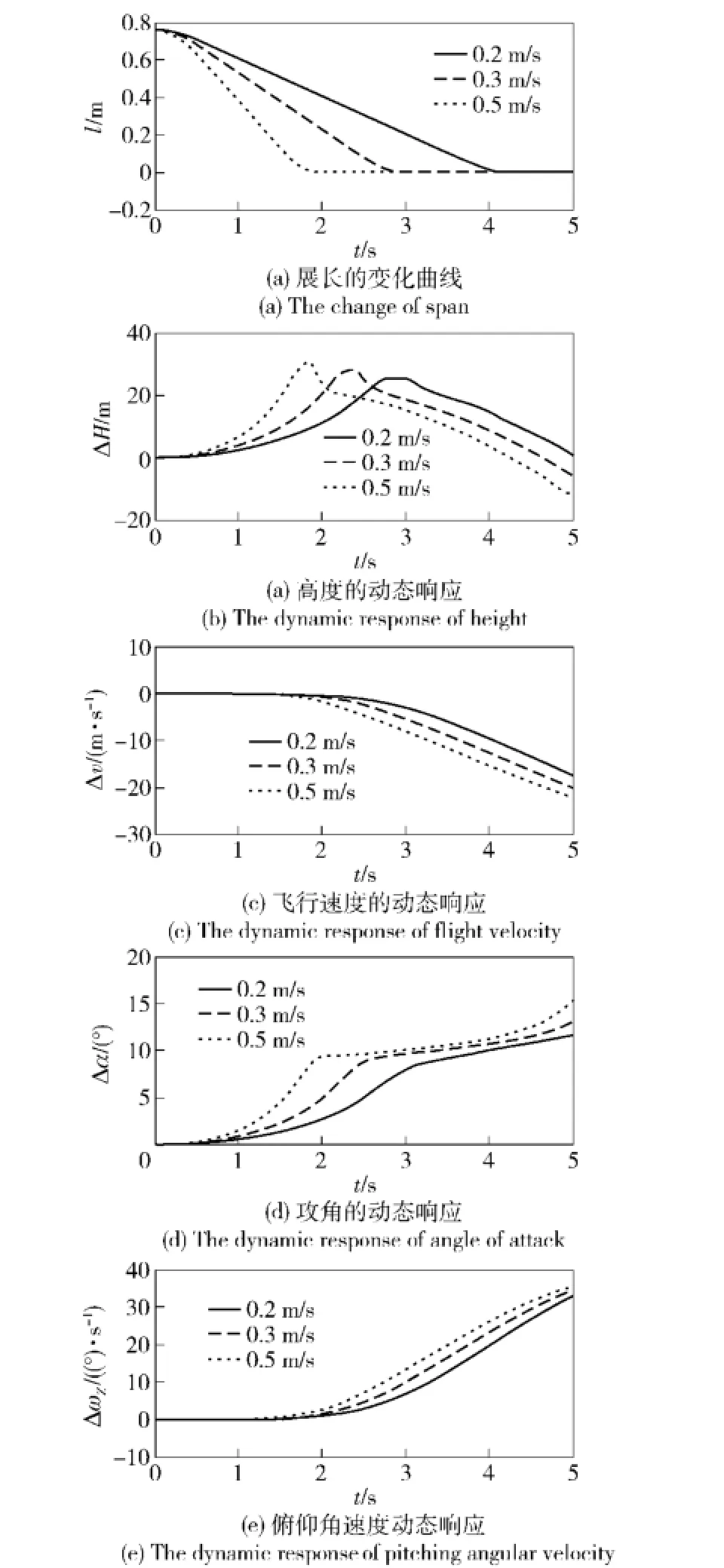
图6 不同展长变化速率下的动态响应Fig.6 The dynamic responses at different morphingspeeds of span
从图6可以看出,由于展长的减小,飞行器呈现先增高后掉高的过程。主要因为在0°后掠角状态展长变化时,质心位置不发生改变,气动作用中心变化也不显著,但此时由于零升力矩系数的减小,导致飞行器呈现缓慢的抬头趋势,俯仰角速度缓慢增加,进而导致攻角增加。由于推力不够,速度持续降低,升力减小,随后飞行器开始掉高,飞行轨迹进入长周期的高度方向震荡衰减过程。同时从图中看出,相较于后掠角,动力学参数对展长的变化速率相对敏感。但增加展长的变化速率不会带来恶劣影响,这对于使用展长的变化来控制飞行器姿态而言很有意义。
4.3 展长和后掠角同时变化时的响应
后掠角和展长同时改变,变化速度为4组,分别为:6°/s,0.3 m/s;6°/s,0.5 m/s;8°/s, 0.3 m/s;8°/s,0.5 m/s.得到的高度、速度、攻角和俯仰角速度等各运动参数的动力学响应如图7所示。
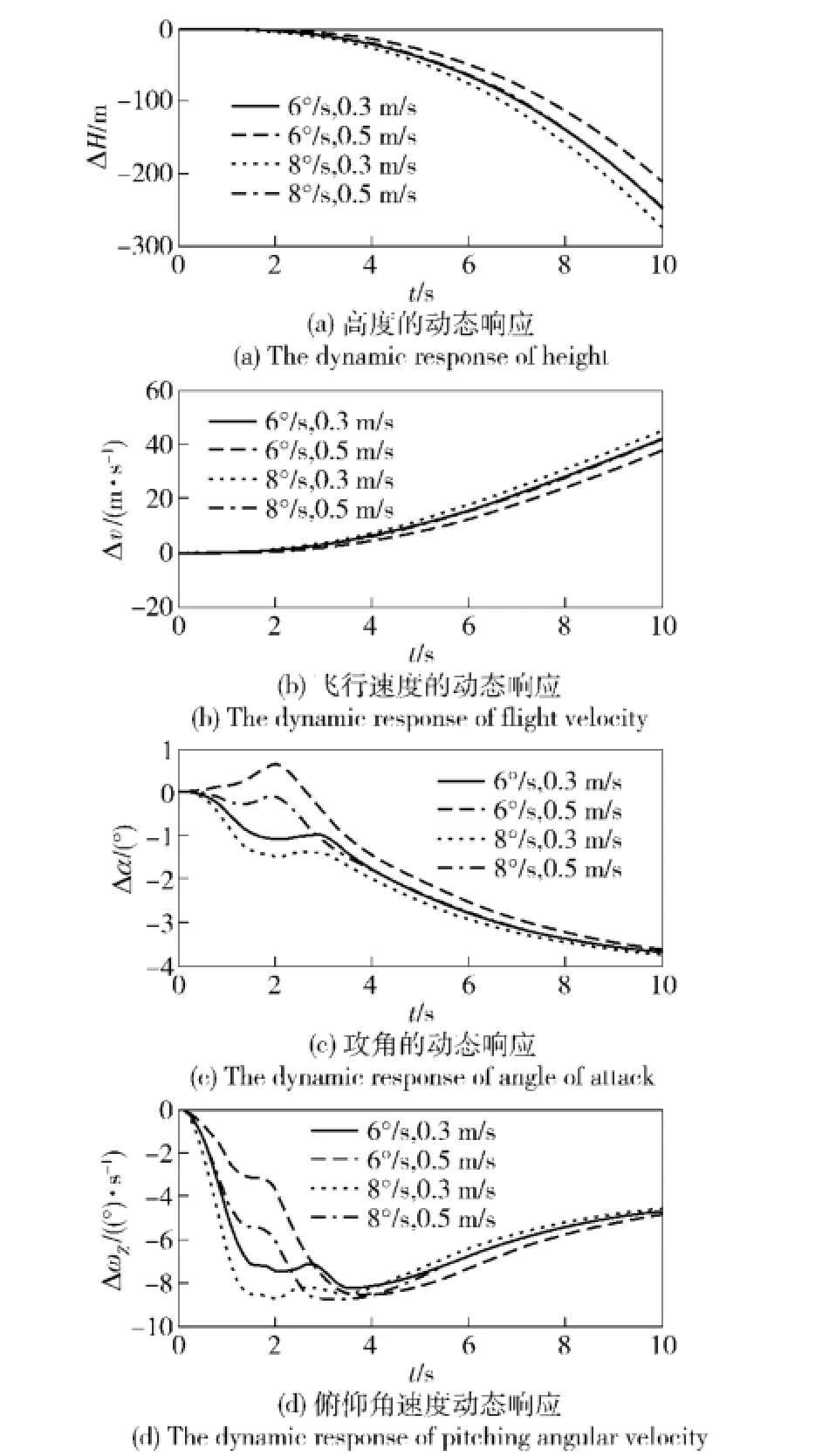
图7 不同后掠角和展长变化速率下的动态响应Fig.7 The dynamicre sponses at different morphing speeds of sweep and span
从图7可以看出,当后掠角和展长同时变化时,后掠角对动态特性的影响占据主导,但是展长的变化对结果起到了平衡和缓和的作用,进而可知通过合适的变形方式和变形速度的结合可以弱化变形过程中的动力学参数波动。
5 结论
本文基于Newton-Euler方法建立了变后掠变展长无人飞行器的多体动力学模型,推导了由变展长和变后掠角所产生的附加力和力矩项。在纵向上解耦简化了动力学方程,基于准定常气动力模型,分析了不同变形形式和变形速率下的飞行器纵向动态响应。仿真结果表明,后掠角和展长的变化对动力学特性影响较大,但变化速度对结果影响不大。通过合适的变形方式和变形速度的结合可以弱化变形过程中的动力学参数波动,进而减小控制系统的负担。
References)
[1] Vasista S,Tong L Y,Wong K C.Realization of morphing wings: a multidisciplinary challenge[J].Journal of Aircraft,2012, 49(1):11-28.
[2] Smith K,Butt J,Von Spakovsky M R.A study of the benefits of using morphing wing technology in fighter aircraft systems[C]∥Proceedings of the 39th AIAA Thermophysics Conference.Miami, Florilia,US:AIAA,2007:25-28.
[3] William A.Crossley.Morphing aircraft sizing using design optimization[J].Journal of Aircraft.2011,48(2):612-622.
[4] 陈钱,尹维龙,白鹏,等.变后掠变展长翼身组合体系统设计与特性分析[J].航空学报,2010,31(3):506-513.
CHEN Qian,YIN Wei-long,BAI Peng,et al.System design and characteristics analysis of a variable-sweep and variable-span wingbody[J].Acta Aeronautica ET Astronautica Sinica,2010, 31(3):506-513.(in Chinese)
[5] Mestrinho J,Gamboa P,Santos P.Design optimization of a variable-span morphing wing for a small UAV[C]∥52nd AIAA/ ASME/AHS/ASC Structures,Structural Dynamics and Materials Conference.Denver,Colorado:AIAA,ASME,ASCE,AHS, ASC,2011:4-7.
[6] An J G,Yan M,Zhou W B,et al.Aircraft dynamic response to variable wing sweep geometry[J].Journal of Aircraft,1988, 25(3):216-221.
[7] 乐挺,王立新,艾俊强.Z型翼变体飞机的纵向多体动力学特性[J].航空学报,2010,31(4):679-686.
YUE Ting,WANG Li-xin,AI Jun-qiang.Longitudinal multibody dynamic characteristics of Z-wing morphing Aircraft[J]Acta Aeronautica ET Astronautica Sinica,2010,31(4):679-686. (in Chinese)
[8] Henry J J,Pines D J.A mathematical model for roll dynamics by use of a morphing-Span Wing[C]∥48th AIAA/ASME/AHS/ ASC Structures,Soructural Dynamics,and Materials Conference. Honolulu,Hawaii:AIAA,ASME,ASCE,AHS,ASC,2007:23-26.
[9] Fossen T I.Guidance and control of ocean vehicles[M].US: John Wiley&Sons Inc,1994:25-28.
Dynamic Modeling and Response of a Morphing UAV with Variable Sweep and Variable Span
YANG Guan-tong,TANG Sheng-jing,ZHAO Lin-dong,GUO Jie
(Key Laboratory of Dynamic and Control of Flight Vehicle,Ministry of Education,Beijing Institute of Technology,Beijing 100081,China)
For morphing flight vehicles,the changes of sweep angle and span have great influence on key parameters such as aerodynamic forces,inertial moments,pressure center and gravity center.A dynamic model of morphing vehicle with variable sweep and span is established based on Newton-Euler method. The additional force and moment generalized by morphing are deduced.The dynamic response aroused by morphing is studied using decoupled longitudinal equations and quasi-steady aerodynamic model.The results indicate that the changes of sweep and span influence the dynamic characteristics severely;however,the effect of different morphing speed is not remarkable.Appropriate strategy of morphing could weaken the fluctuation of dynamic parameters and relieve the burden of control system.
applied mechanics;UAV;variable sweep and variable span;dynamic modeling;dynamic response
V212.1
:A
1000-1093(2014)01-0102-06
10.3969/j.issn.1000-1093.2014.01.015
2013-04-22
航空科学基金项目(2012ZA72002)
杨贯通(1986—),男,博士研究生。E-mail:ygt@bit.edu.cn;
唐胜景(1959—),男,教授,博士生导师。E-mail:tangsj@bit.edu.cn
