改进的投影寻踪技术在实际预报中的应用

2014-06-26吴成明王婷乐姚维为董文静

水科学与工程技术 2014年2期

吴成明，王婷乐，姚维为，董文静，刘溪

（三峡大学电气与新能源学院，湖北宜昌 443002）

梯级水电站水库群联合调度的目的是在时间和区域上组合运用各种水库的调节能力，科学地控制各时段末（汛初、汛末、年末、供水期末）的库水位，相互补偿调节，满足电网安全、优质运行与可靠供电的要求，充分利用水量和水头。随着经济发展要求的不断提高，人们对于水电站调度预见期的要求也在不断提高，短期的水电站入库流量预报已经不能满足现阶段水电站调度的需要，而作为水电站中期调度的基础，中期入库流量预报的提出是对短期入库流量预报的一个重要补充，对充分发挥梯级水电站的经济效益具有重要意义。

1 改进投影寻踪预测技术

1.1 投影寻踪

投影寻踪［1，4］是处理和分析高维观测数据，尤其是来自非正态总体的高维数据的一类统计方法。投影寻踪的基本思想是将高维数据投影到低维（1～3）子空间上，寻找出所反映原高维数据的结构或特征的投影，以达到研究和分析高维数据的目的。

投影寻踪技术是解决高维空间不能克服的 “维数祸根”的有效途径。

投影寻踪回归模型表示为：

1.2 对传统投影寻踪回归的改进

1.2.1 投影问题

投影问题即通过对系统输入信息的分析，得到最能反映系统特征的投影方向——最优投影方向。传统投影寻踪预测方法中，模型中的α是通过高斯——牛顿优化，在这个过程中，涉及一系列的包括矩阵求逆的高等数学运算，编程求解非常困难，而且影响计算速度和精度。

本文采用实数编码的遗传算法代替高斯——牛顿算法进行投影方向优化。当遗传算法与投影寻踪方法相结合时，遗传算法的适应度是投影指标函数，初始种群为任意M个投影方向，通过遗传、交叉、变异的过程，对M个投影方向进行搜索，以得到使投影指标最优的最佳方向。

综上所述，实数编码的遗传算法优化投影方向的算法如下：

设m为解空间的维数，popsize为种群的规模，chrom（popsize）为投影方向的实数编码，αi为投影方向α的分量，Q为投影指标，即为适应度fitness，pcross为交叉概率，pmutation为变异概率，投影方向的个数和循环次数也可根据具体情况而定。

（1）步骤1。在m维解空间按种群规模popsize随机选取 m 组在［0，1］区间随机数 chrom（i）（i=1～popsize）作为优化的编码，并且每组编码对应一个投影方向。

（2）步骤 2。αi=2×chrom（i）-1，且‖α‖=1，计算Q=f（α）。

（3）步骤3。按适应度大的原则，进行交叉、变异操作，从结果中选取popsize个适应度也即投影指标大的编码，返回步骤2，直到达到设定的循环次数。

实数编码的遗传算法具有计算简单的特点，只有简单的加减乘除和交换运算，没有复杂的导数和矩阵运算。

1.2.2 寻踪问题

寻踪问题即样本系列投影到低维空间后，传统的投影寻踪回归通过平滑后取中位数的非参数方法估计岭函数。考虑到岭函数fk无具体的函数表达式，需要通过庞大的函数表来来给出，计算导数时需要用差分法来代替微分，预报时用函数表来内插，计算非常复杂，编程求解困难，通过利用参数非线性Hermite多项式来代替非参数方法来估计岭函数，避免庞大的函数表，且能保证岭函数拟合的精度。

（1）步骤1。选择一个初始的投影方向，并将预报因子投影在选择方向上。

（2）步骤2。找到拟合最好的岭函数，确定多项式的阶数R，利用最小二乘法确定Hermite多项式的权重系数c。

对于一个预见期为10d的中期入流预报，建立多因子输入、单因子输出的改进投影寻踪回归模型如下：

根据以上分析改进的思想，改进的投影寻踪回归预测技术流程图如图1所示。

图1 改进的投影寻踪回归预测技术流程图

根据流程图编制改进的投影寻踪回归应用程序，并用于制定杂谷脑流域的预报方案。在本设计中，采用Hermite函数进行拟合时，Hermite多项式的阶数为R=5，遗传算法的种群规模popsize=100。

3 实例应用

杂谷脑流域干流上有杂谷脑水文站和桑坪水文站，桑坪站位于杂谷脑河末端，对上游各水电站可利用度较小，因此选择杂谷脑水文站流量数据作为主要的研究数据，下游桑坪站数据作为参考数据。选取1952～1987年杂谷脑水文站流量为基本实验数据，预留1985～1987年洪水流量为检验数据。以本文提出的改进的投影寻踪回归方法建立洪水预报模型。

3.1 洪峰预报

从1952～1953年和1986～1987年时段为10d资料中，选取33个具有代表性的洪峰点，其中1952～1953年大于600m3/s的19个洪峰点作为参数率定数据，用于确定投影寻踪回归模型的参数及遗传算法的4个参数，投影与拟合效果如图2所示。1986～1987年大于100m3/s的14个洪峰点用于校验模型，校验与拟合效果如图3所示。

图2 洪峰模型投影与拟合效果

图3 洪峰模型校检与拟合效果

洪峰模型投影与拟合的R2=0.9525，且相对误差均在10%以内；检验与拟合的相对误差最大值为7.30%，根据我国水情预报规范，相对误差小于20%即合格，拟合与校验的效果均在10%以内，可见拟合效果较好。

3.2 洪水过程预报

选取1952～1953年时段为10d的洪水过程，用改进的投影寻踪预报技术建立洪水过程预报模型，率定模型参数；预留1986～1987年洪水过程用于校验。1952～1953年洪水过程投影与拟合如图4所示，1986～1987年洪水过程校验与拟合如图5所示。

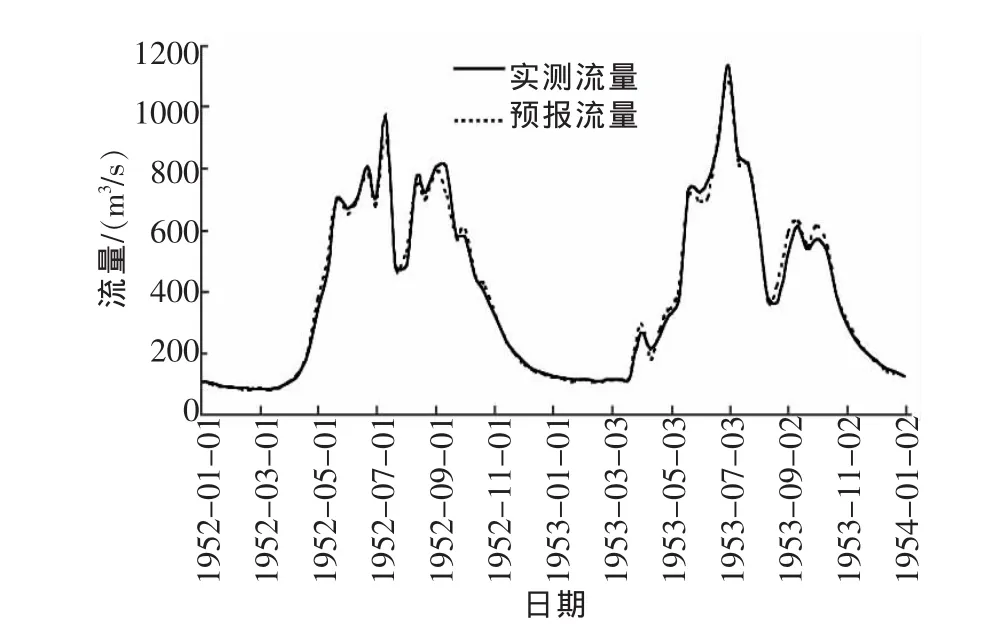
图4 洪水过程投影与拟合

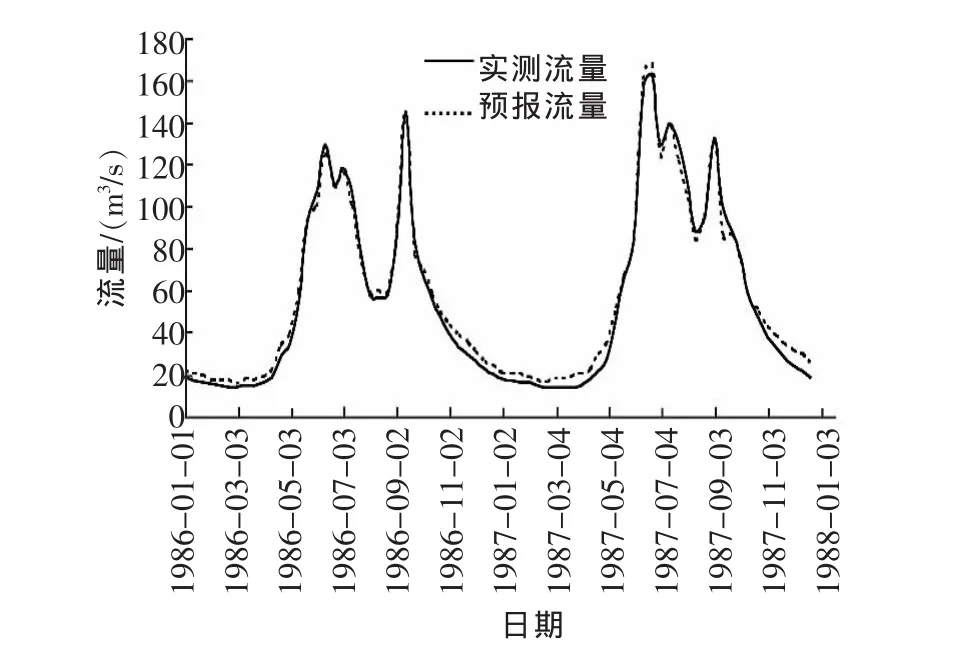
图5 洪水过程校验与拟合

从图4和图5可以看出，流量变化趋势拟合较好，相对误差均小于20%，投影拟合精度达到100%，而校验拟合合格率也达到84.72%，满足预报精度。1986～1987年的实测平均流量55.39m3/s，对应的预报平均流量56.86m3/s，相对误差2.7%；1952～1953年实测平均流量387.73m3/s，对应的预报平均流量383.06m3/s，相对误差仅1.21%。

从流量总体变化趋势上看，无论是投影拟合和检验拟合，预报流量和实测流量的变化趋势都基本相同。相比较于枯水期，丰水期预报相对误差较小，预报精度高，这与水文预报的基本要求相符。而且，从洪峰流量上比较，模拟结果较好，预报洪峰流量和实测洪峰流量基本相同。更为重要的是，洪水过程预报中的洪峰流量与洪峰预报中的洪峰流量基本一致，这将洪峰预报与洪水过程预报充分结合在一起，对预报精度的检验具有重要的参考价值。

翻阅历史数据资料，造成误差较大的原因可能存在以下因素：①中长期水文预报模型很多，但是没有一种模型对所有水文序列都适用。预报模型改进后，仍然存在很多不足，需要不断改进。同时中长期预报受很大因素的制约，需要综合各因素的影响，这里只考虑前期流量因素的影响，虽然探讨了可行性，但是仍然存在很大的局限性；②在实际观测过程中，浮标系数选择存在差异，对测量结果产生影响。