直接空冷系统流动特性的多尺度模拟研究

胡和敏，杜小泽，杨立军，杨勇平

（华北电力大学 电站设备状态监测与控制教育部重点实验室，北京102206）

近年来，直接空冷机组以其显著的节水优势，在我国北方“富煤缺水”地区取得了很大发展.然而，火电机组空冷岛的热流系统具有明显的多尺度特性，其影响因素包括：10-3m 数量级的翅片结构；101m数量级的Λ 型空冷凝汽器单元；空冷岛的换热性能还易受到电厂建筑，甚至103m 数量级的地形地貌的限制.不同特征尺度上空气流场的湍流涡旋及其级联破裂过程共同对空冷系统散热性能产生影响.

在空冷岛的设计和运行阶段，计算流体力学（CFD）方法经常被用于研究空冷岛的对流换热特性［1-4］.由于时间和计算资源有限，很难实现对跨尺度区域的同步模拟.且这些研究都是在某种假设的前提下，在某1个或2个尺度上进行的，而忽略其他尺度的影响.随着对空冷岛热流系统研究的逐步深入，需要寻求一种能够解决空冷岛跨尺度热流问题的模拟方法.

多尺度问题广泛存在于自然科学的各个领域［5-6］，如环境科学、生物科学、材料科学、地壳运动以及流动传热等.近年来，多尺度科学引起了学者们的广泛关注，其研究手段也得到了长足发展，其中一个典型的模拟方法是对不同尺度计算区域建立不同的物理模型，其数值解在大小尺度区域界面上耦合［7］.Nie等［8］采用这种分区建模界面耦合的方法来研究顶盖驱动流动的多尺度问题，其中采用分子动力学（MD）方法来描述顶盖附近的流动，用N-S方程模拟其他区域的流动.Wu等［9］将直接模拟技术和N-S方程相结合来模拟分析包括连续和稀薄形态的高速气体流动.栾辉宝等［10］构造了格子-Boltzmann方法（LBM）和有限容积法（FVM）的耦合模型，给出了重构算子，并在典型流动传热问题中得到了验证.Tang 等［11］用一种多层网格嵌入的多尺度方法来分析印刷板的流动和换热特征，这种方法用粗网格来离散整体模型，而后逐渐向所关心的区域细化网格.

Rambo［12］基于正交分解方法（POD）提出了一种新的多尺度方法来预测数据中心冷却系统的温度场和速度场.其中，对风室和服务器构件分别建立关于温度场和速度场的POD 低维模型.在得到上游模块POD 解的基础上，利用两个模块之间界面上的通量守恒法（FMP）来得到下游模块的POD 解.

为了更好地解决火电厂直接空冷系统的跨尺度热流问题，笔者在前人工作的基础上，提出一种新的多尺度湍流模拟方法.在小尺度区域建立POD 模型并求解，再将大小尺度界面上POD 解的参数信息提取出来，作为边界条件赋值给大尺度区域.在此基础上，用Fluent商业软件来对大尺度区域进行CFD求解，预测了二维空冷单元的跨尺度流动特征.

1 物理数学模型

图1给出了Λ 型空冷单元的示意图.由图1可知，Λ 型布置的空冷单元由汽轮机排汽管、翅片管束、轴流风机以及风筒组成.由轴流风机引入的空气流经翅片管束并与之发生对流换热，将汽轮机排汽的凝结潜热带走.

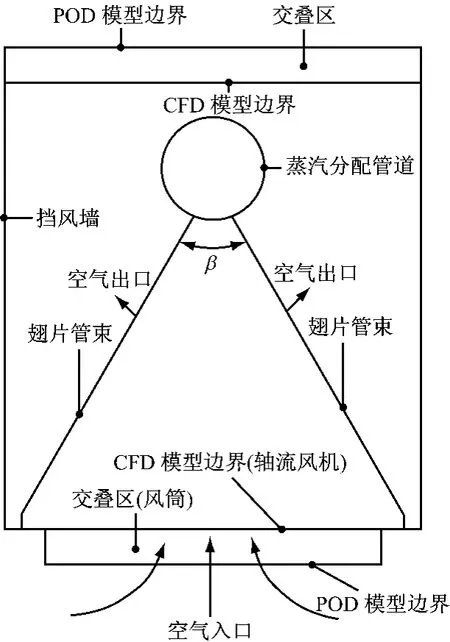
图1 Λ 型空冷单元的示意图Fig.1 Schematic diagram of theΛ-frame air-cooled condenser

根据Oliveira等［13］的研究结果，为了得到与计算域大小无关的数值解，为POD 的低维模型提供精确的快照数据，计算域x方向和y方向的坐标取值范围分别为（0，472.1）和（0，138），模型的细节尺寸见图2.

图2 空冷单元的物理模型及其计算域Fig.2 Physical model of the ACC unit and its computational domain

1.1 控制方程

假设空气为不可压缩流体，模型计算域的流动特性满足如下控制方程

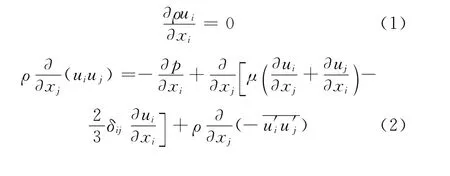
其中

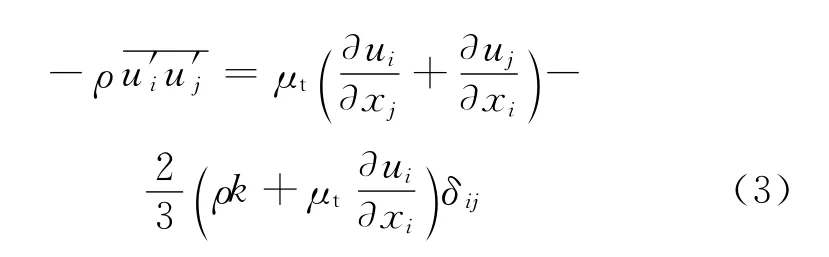
式中：ρ为空气密度；ui和uj分别表示x（或y）方向的速度分量；p为压力；μ和μt 分别表示动力黏度和湍流黏度；δij为Kroneker符号.

数值模拟采用标准k-ε两方程模型，湍动能k和湍流耗散率ε的控制方程如下

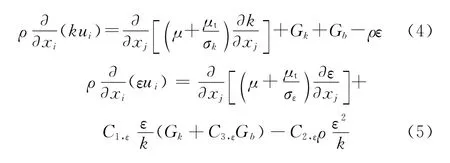
式中：Gk和Gb分别表示由平均速度梯度和浮升力所产 生 的 湍 动 能；C1，ε、C2，ε和C3，ε为 常 数，其 中C1，ε＝1.44，C2，ε＝1.92.

1.2 边界条件

计算域迎风面（x＝0）采用速度入口边界条件，大气层内空气平均速度大小随海拔高度按指数规律变化

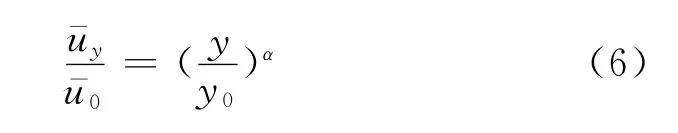
式中：y和分别为任意海拔高度及其平均速度大小；y0和分别为参考高度及其平均速度大小，本文取y0＝10m；α为当地的地面粗糙度，根据日本荷载规范［14］，取α＝0.2.

翅片管束采用集总参数的散热器模型，流经管束的无量纲压降为垂直于翅片表面速度分量的多项式.

轴流风机简化为风机边界条件.根据风机性能曲线，将流经风机平面的压力跃变Δp拟合为轴向速度分量w的4次多项式

计算域出口面（x＝472.1）采用出流边界条件.

1.3 数值解法

根据文献［15］中对模型进行的网格无关性检验结果，模型整体网格数为7.64×104，其中大尺度区域采用特征尺度为1.00大小的网格进行划分.而空冷单元及其周围的小尺度区域所包含的1.05×103个网格的特征尺度为0.35.整个模型计算域均采用四边形网格进行划分.

模型的控制方程采用有限差分法进行离散；除了压力项采用标准差分格式外，其他方程均采用一阶迎风差分格式；压力与速度的耦合方式采用Simple算法；用Fluent商业软件对模型进行求解.当所有变量的残差均小于10-10时，认为计算结果收敛.

2 正交分解方法

POD 模型的计算域如图1所示，由CFD 计算得到的关于变量Θ的快照被正交分解为一组POD基φ，即建立了POD 低维模型.在研究范围内的任意工况下Θc可以用这组POD 基线性表示，从而得到Θ的POD 解.

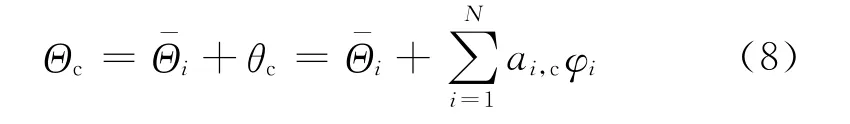
式中：源项为N个CFD 模拟结果的平均值.快照空间｛θ1，θ2，…，θi，…，θN｝被正交分解为N个POD基φi，其中θi＝Θi-.

对速度u、湍动能k和湍流耗散率ε3个变量建立POD 低维模型，用3次样条插值得到POD 基的权系数ai，c.

更多关于POD 方法的理论基础、特点及其实际操作过程（snapshot法）可参考文献［15］.

3 多尺度湍流模拟方法

传统CFD 方法中，基于计算资源和计算精度的综合考虑，模型中流动结构复杂的空冷单元附近区域需采用细网格进行划分，而其他区域则可采用相对粗网格划分.笔者认为图1所示的细网格划分的空冷单元区域为小尺度区域，除此之外的图3所示的区域则为大尺度区域；其中交叠区共同属于大小尺度区域.采用POD 方法快速准确地预测细网格划分的小尺度区域的流动形态；而粗网格划分的大尺度区域的流动形态则用N-S 方法描述.将从POD解中提取出的大小尺度界面上的变量信息赋值于大尺度区域，以实现大小尺度的界面耦合.多尺度湍流模拟方法的具体计算步骤如下：

（1）在风向为（1，0），取4m／s、5m／s、6m／s和7m／s的情况下，对图2所示的物理模型进行CFD 计算，得到数值解.

（2）从CFD 数值解中取出图1的小尺度区域中关于u、k和ε3个变量的快照数据，采用snapshot法对其建立POD 低维模型.

（3）采用3 次样条插值法得到试验工况为4.7m／s、5.7m／s和6.6m／s时的POD 解.

（4）从3个试验工况的POD 解中提取出3个变量在CFD 模型边界面上的参数分布.

（5）将3个参数分布以速度入口边界条件的形式赋值于图3所示的大尺度区域，而后利用Fluent商业软件来求解包含交叠区域在内的N-S方程.

假定传统CFD 方法同时对整个区域（包含大小尺度在内）的N-S方程进行迭代求解的计算结果为真值，多尺度湍流模拟方法所得的解中，某变量Θ相对于传统CFD 解的误差可表示为

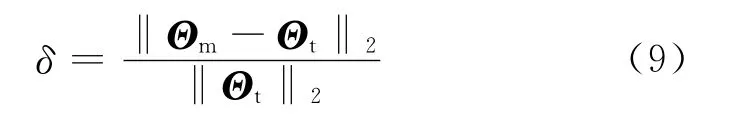
式中：‖‖2表示2-范数；Θm和Θt分别为多尺度湍流模拟方法和传统CFD 方法得到的解.

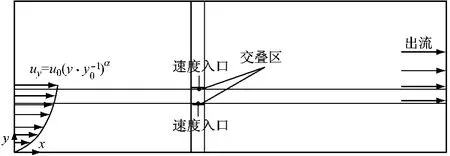
图3 CFD模型及其计算域Fig.3 CFD model and its computational domain

4 结果与分析

图4给出了3个试验工况下POD 解的截断误差随POD 基数目的变化规律.由于最后一个POD基的失真，将其舍去.从图4可以看出，随着POD 基数目的增大，误差逐渐减小.在只有4个快照的情况下，所得POD 解中3个变量的误差均小于4.35%，而速度的误差可以控制在0.50%以内.对比3个试验工况的误差曲线可以看出，工况＝5.7m／s下3个变量所能达到的计算精度最高，其次是＝6.6 m／s，工况＝4.7m／s的精度最差.这是因为工况＝5.7m／s所对应的湍流状态与源项所对应的湍流状态最接近，因此可以得到更高精度的POD解.当试验工况所对应的湍流状态与源项所对应的湍流状态偏差较大时，用POD 方法预测得到的结果精度会有所下降.这是POD 方法所固有的弊端，可以通过POD 补集（PODc）方法［10］得到改进.

表1给出了大尺度区域CFD 计算所得的误差.由表1可知，与传统CFD 计算结果相比，所有变量的误差均小于3.55%，其中速度的误差不大于0.40%，湍动能和湍流耗散率的误差有所增大，压力的误差可以控制在1.20%左右.大尺度区域的CFD解与小尺度区域的POD 解的误差随u的变化规律不尽相同.这是因为小尺度区域的湍流状态只是通过大小尺度之间界面上的变量信息对大尺度区域的CFD 计算起作用.而大尺度区域的CFD 迭代过程还会受其他边界条件、计算模型和离散方式等的综合影响.

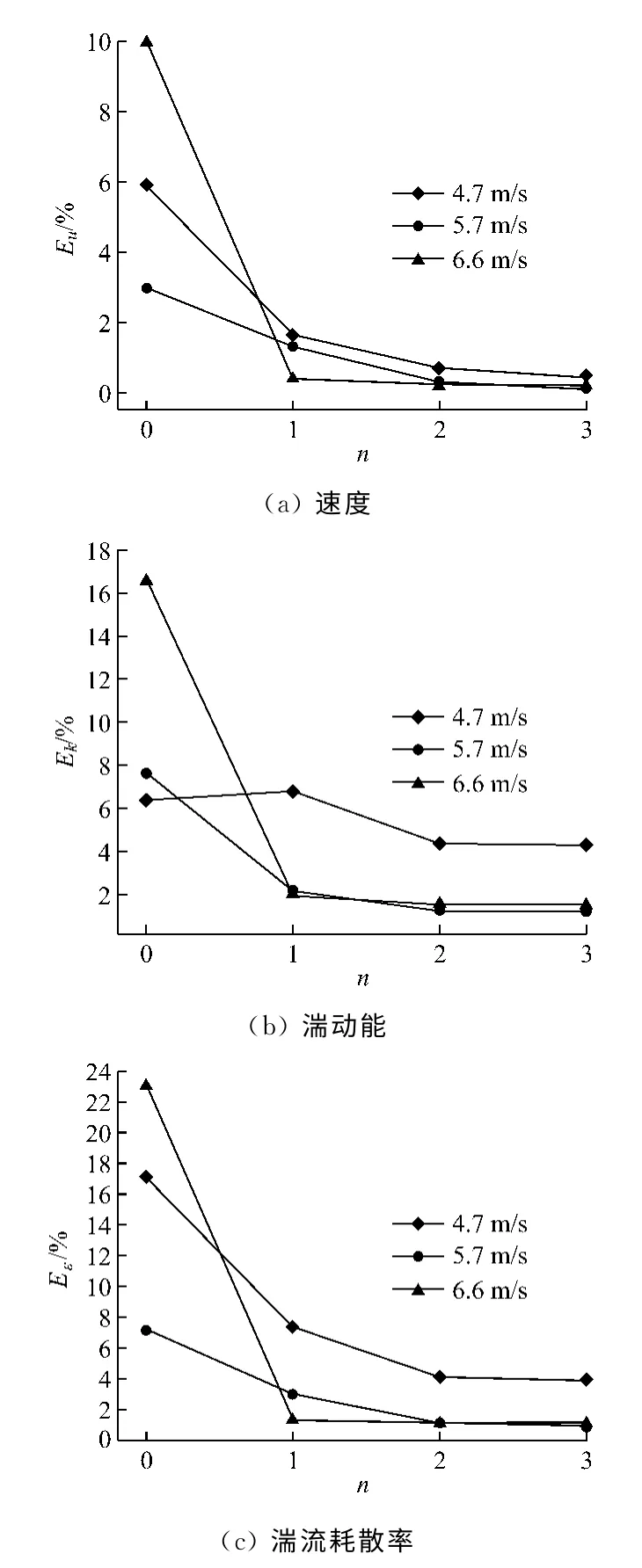
图4 POD解的截断误差随POD基数目的变化Fig.4 Change of truncation error of POD solution with POD mode number

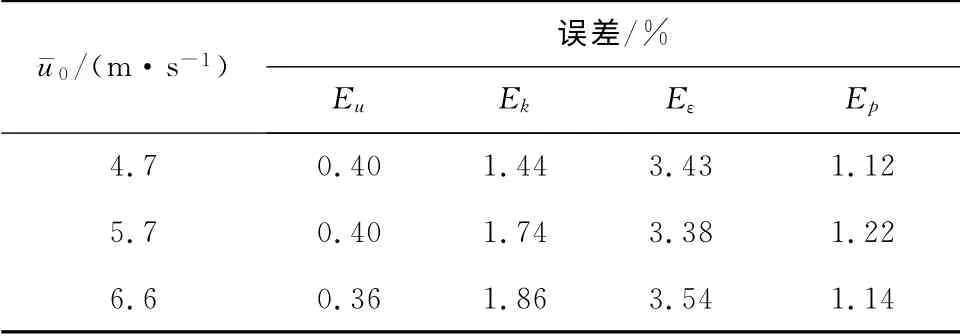
表1 大尺度区域的误差Tab.1 Errors for the large-scale region

图5为试验工况＝5.7m／s时，多尺度湍流模拟方法与传统CFD 方法计算所得的速度流线图.图5（a）为大尺度区域的流线图，图5（b）则是在图5（a）基础上增加了小尺度区域的POD 计算结果.与图5（c）所示的传统CFD 计算结果进行对比发现，2种方法的计算结果具有很高的吻合度.因此，笔者所提出的多尺度湍流模拟方法能够很好地描述空气流经空冷单元所产生的尾涡.在大小尺度区域分开求解的情况下，揭示出空气在风机、翅片管束、挡风墙以及环境风共同影响下的流动特性，能够将大小尺度的湍流状态关联起来，从而很好地揭示出空冷单元的多尺度流动特征.

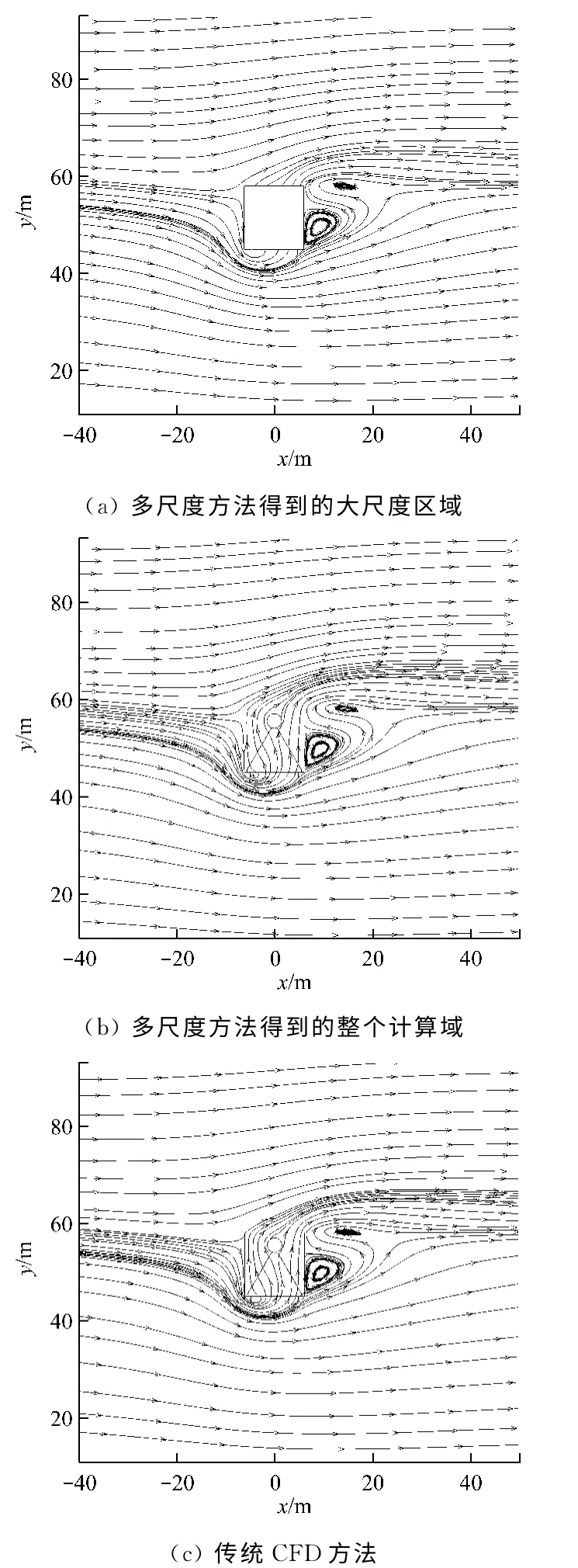
图5 试验工况＝5.7m／s时的速度流线图Fig.5 Velocity streamlines in the test case of＝5.7m／s

图6给出了试验工况＝5.7m／s时的压力云图.由图6可知，与传统CFD 方法计算结果相比，二者所得的压力云图十分吻合.另外，从图4所示的小尺度区域各变量的误差和表1列出的大尺度区域的误差中，也很好地说明多尺度湍流模拟方法在处理二维空冷单元多尺度流动问题上具有足够高的精度.

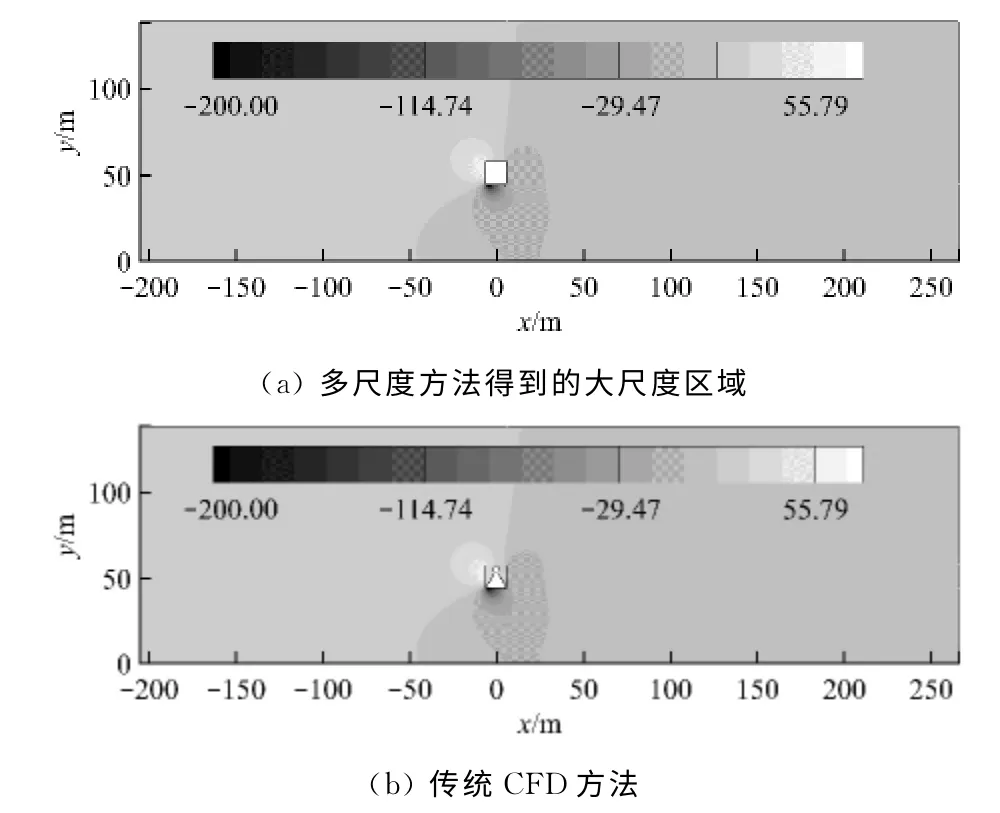
图6 试验工况u＝5.7m／s时的压力云图Fig.6 Pressure contours in the test case of ＝5.7m／s

由于POD 计算方法的准确性和高效性，几乎可以忽略POD 模型求解所用的时间，因而只需考察多尺度方法中大尺度区域的计算时间.以工况＝5.7 m／s为例，用所提出的多尺度方法迭代300次需要102s，而用传统CFD 方法则需要110s.由于模型中小尺度区域的网格数所占的比例较小，而用多尺度方法对大尺度区域进行CFD 计算时，在处理边界信息上需要花费一定的时间.因而在迭代次数相等的情况下，多尺度方法的计算时间节省不多.若将本文所述的多尺度湍流模拟技术推广至直接空冷系统中三维小尺度空冷单元与大尺度的电厂建筑乃至地形地貌的尺度耦合中去，效果会非常明显.由于三维空冷单元结构的复杂性，需要用极细网格进行划分才能保证计算的准确性，其离散网格将会占模型网格总数的半数以上.在大尺度区域的CFD 计算过程中，细网格的小尺度区域处于反激活状态，所用的计算资源和时间将会明显节省.

表2为用2种方法对3个试验工况进行求解，达到收敛时所需要的迭代次数.从表2可以看出，由于给定了边界信息，使多尺度方法比传统CFD 方法更容易收敛，从而提高了计算效率.

表2 2种方法计算所需的迭代次数Tab.2 Iteration number required by both the methods

5 结 论

（1）考虑横向环境风的作用，利用POD 方法对直接空冷凝汽器单元中空气流动的变量分布进行了精确高效的预测.

（2）利用从空冷单元小尺度区域的POD 解中提取跨尺度界面上的变量信息，再赋值于大尺度区域的方法，可以准确地描述环境风流经空冷单元的湍流特征，实现跨尺度界面耦合.

（3）分开求解小尺度区域的POD 模型和大尺度区域的CFD 模型，可大大节省计算资源.在保证一定计算精度的基础上提高计算效率.

［1］周兰欣，张情，李卫华.直接空冷凝汽器喷雾增湿系统的结构优化［J］.动力工程学报，2011，31（2）：148-152. ZHOU Lanxin，ZHANG Qing，LI Weihua.Structural optimization for spray humidification system of a direct air-cooled condenser［J］.Journal of Chinese Society of Power Engineering，2011，31（2）：148-152.

［2］石维柱，安连锁，张学镭，等.直接空冷机组喷淋冷却系统的数值模拟和性能分析［J］.动力工程学报，2010，30（7）：523-527. SHI Weizhu，AN Liansuo，ZHANG Xuelei，etal，Numerical simulation and performance analysis of spray cooling system in direct air cooling units［J］.Journal of Chinese Society of Power Engineering，2010，30（7）：523-527.

［3］周兰欣，崔皓程，仲博学.主导风向对直接空冷凝汽器换热效率的影响［J］.动力工程学报，2010，30（2）：138-142. ZHOU Lanxin，CUI Haocheng，ZHONG Boxue.Influence of prevailing wind direction on heat transfer efficiency of direct air-cooled condensers［J］.Journal of Chinese Society of Power Engineering，2010，30（2）：138-142.

［4］刘达，杨建国，张兆营，等.水平挡板改善直接空冷凝汽器流场特性的数值模拟［J］.动力工程学报，2011，31（12）：949-954. LIU Da，YANG Jianguo，ZHANG Zhaoying，etal.Numerical simulation on flow field of direct air-cooled condenser improved by horizontal baffles［J］.Journal of Chinese Society of Power Engineering，2011，31（12）：949-954.

［5］何国威，夏蒙棼，柯孚久，等.多尺度耦合现象：挑战和机遇［J］.自然科学进展，2004，14（2）：121-124. HE Guowei，XIA Mengfen，KE Fujiu，etal.Phenomena of coupling multiscale：challenges and opportunities［J］.Progress in Natural Science，2004，14（2）：121-124.

［6］柴立和.多尺度科学的研究进展［J］.化学进展，2005，17（2）：186-191. CHAI Lihe.Recent progress of multiscale science［J］.Progress in Chemistry，2005，17（2）：186-191.

［7］陶文铨.传热与流动问题的多尺度数值模拟：方法与应用［M］.北京：科学出版社，2008.

［8］NIE Xiaobo，CHEN Shiyi，ROBBINS M O.Hybrid continuum-atomistic simulation of singular corner flow ［J］.Physics of Fluids，2004，16（10）：3579-3591.

［9］WU J S，LIAN Y Y，CHENG G，etal.Development and verification of a coupled DSMC-NS scheme using unstructured mesh［J］.Journal of Computational Physics，2006，219（2）：579-607.

［10］栾辉宝，徐辉，陈黎，等.有限容积法与格子Boltzmann方法耦合模拟传热流动问题［J］.科学通报，2010，55（32）：3128-3140. LUAN Huibao，XU Hui，CHEN Li，etal.Coupling between FVM and LBM for heat transfer and fluid flow problems［J］.Chinese Science Bulletin，2010，55（32）：3128-3140.

［11］TANG L，JOSHI Y K.A multi-grid based multi-scale thermal analysis approach for combined approach for combined mixed convection，conduction，and radiation due to discrete heating［J］.Journal of Heat Transfer，2005，127（1）：18-26.

［12］RAMBO J D.Reduced-order modeling of multiscale turbulent convection：application of data center thermal management［D］.Atlanta，USA：Georgia Institute of Technology，2006.

［13］OLIVEIRA P J，YOUNIS B A.On the prediction of turbulent flows around full-scale buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2000，86（2／3）：203-220.

［14］JUN Kanda.AIJ-RLB-2004AIJ recommendations for loads on buildings［S］.Japan：Architectural Institute of Japan，2004.

［15］DU Xiaoze，HU Hemin，SHEN Yinqi，etal.，Reduced order analysis of flow and heat transfer for aircooled condenser of power generating unit［J］.Applied Thermal Engineering，2013，51（1／2）：383-392.