非傍轴部分相干厄米-余弦-高斯光束传输特性
2014-06-23邝爱华
李 平,邝爱华
非傍轴部分相干厄米-余弦-高斯光束传输特性
李 平1,邝爱华2
(1.黄淮学院信息工程学院,驻马店463000;2.郑州电子信息工程学校,郑州450007)
为了研究非傍轴部分相干厄米-余弦-高斯光束传输特性,运用Wigner分布函数法,从空间域和频率域对非傍轴部分相干厄米-余弦-高斯光束传输特性进行了理论分析,得出了该光束1阶情况下在空间、频率域系统的解析传输公式及光强分布表达式,分析了这些表达式中3个主要参量f,fσ和g对厄米-余弦-高斯光束在自由空间传输的影响。结果表明,在调制参量g不变时,束腰参量f和相干参量fσ对非傍轴部分相干厄米-余弦-高斯光束的非傍轴性起了至关重要的作用;非傍轴部分相干厄米-余弦-高斯光束在传输过程中随着g的改变,不能保持其光强分布形状,有前移趋势。
激光光学;非傍轴部分相干厄米-余弦-高斯光束光束;Wigner分布函数;传输表达式
引 言
近年来,随着科技的发展,激光器的种类也越来越多。学者对于不同光束的传输特性颇有研究,如平顶高斯光束通过扩束系统的传输特性研究[1]和高斯光束的光谱传输特性分析[2]等。对于半导体多模振荡引起的激光束,DUAN和LÜ[3]提出了非傍轴部分相干的概念,并做了相应激光束的研究,作者在此基础上,利用Wigner分布函数法对非傍轴部分相干TEM10厄米-余弦-高斯(Hermite-cosine-Gaussian,HCsG)光束在自由空间的传输特性进行深入研究,并利用MATLAB软件进行数值计算与仿真分析。
1 理论推导
假定非傍轴部分相干TEM10厄米-余弦-高斯光束在空间频率域z=0平面时,在x方向上线性极化的交叉谱密度为[4]:
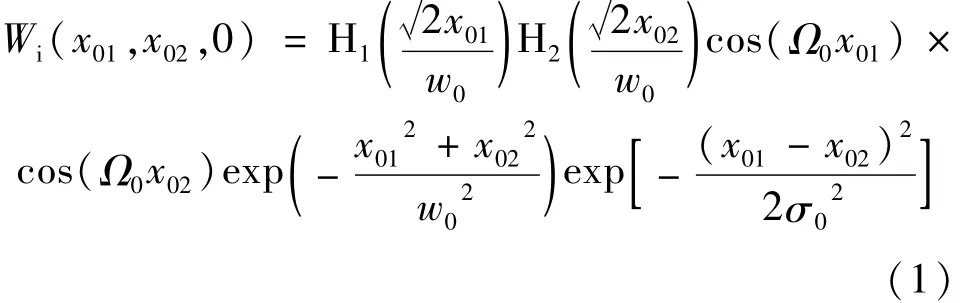
式中,w0,σ0分别是光束的束腰参量和相干长度,H1和H2代表1阶厄米多项式,Ω0为与余弦函数相关的参量,下标i表示在输入平面上,由Wigner分布函数传输关系式[5],在输入平面(源场z=0)和输出平面z时的Wigner分布函数分别为[6]:
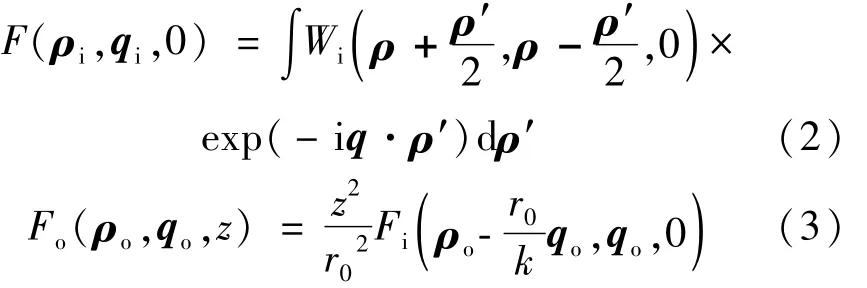
(2)式中,ρ=ix+jy,表示空间位置矢量;i,j分别表示沿着x,y轴方向的单位矢量;ρ′为空间位置矢量的增量,dρ′=∫…dx′dy′;q=iu+jv,表示空间频率矢量,u,v分别为x,y方向上的空间频率。(3)式中的k=为波数[7],λ为激光束在自由空间波长,下标o表示为输出Wigner分布函数。由(2)式及(3)式得到非傍轴部分相干TEM10厄米-余弦-高斯光束在自由空间中的传输表达式为:
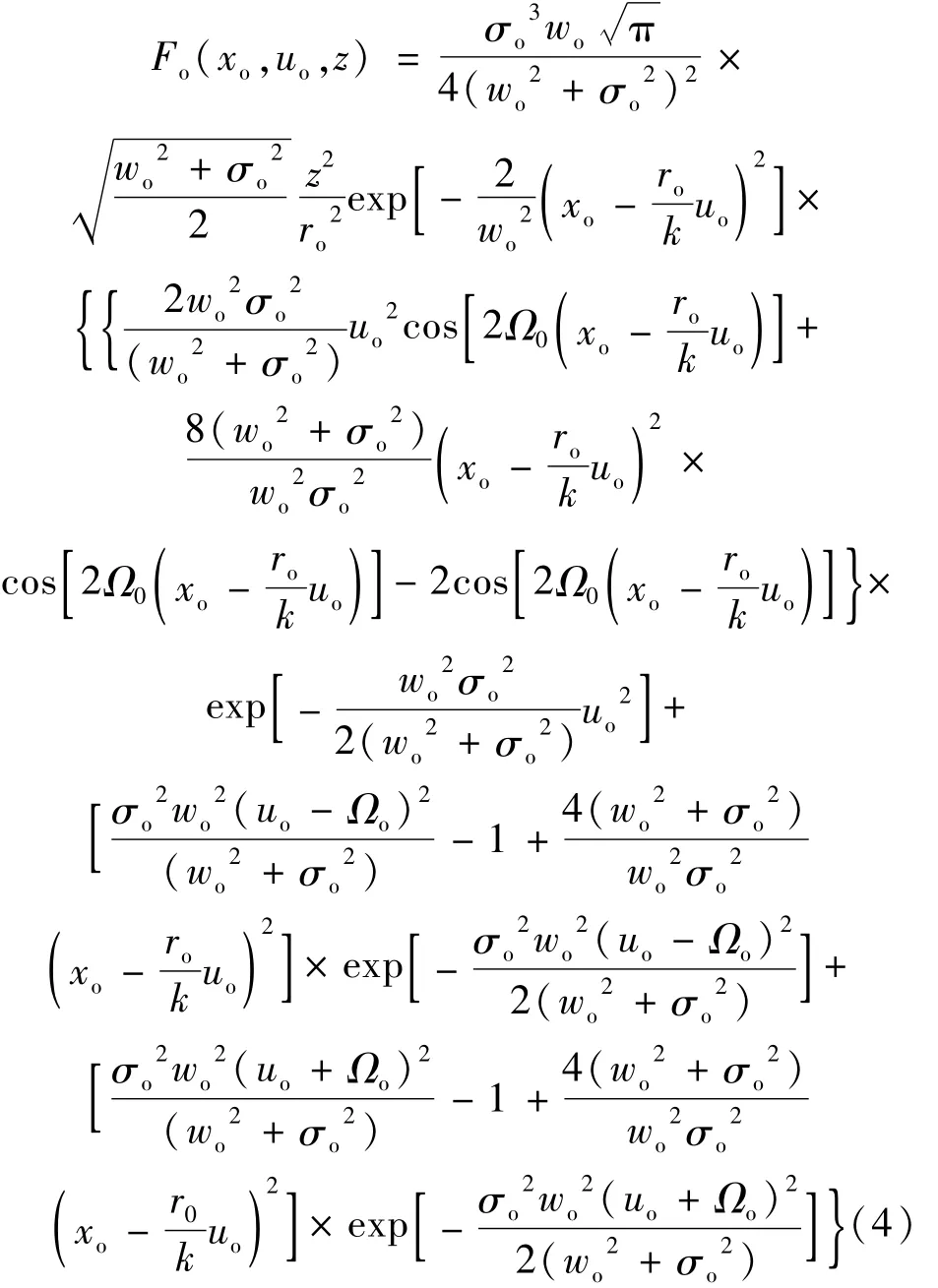
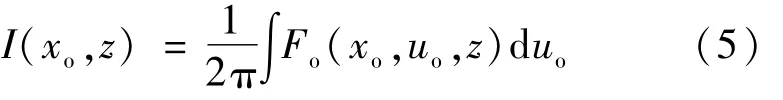
由(5)式可以得到非傍轴部分相干TEM10厄米-余弦-高斯光束在自由空间中的光强分布为:
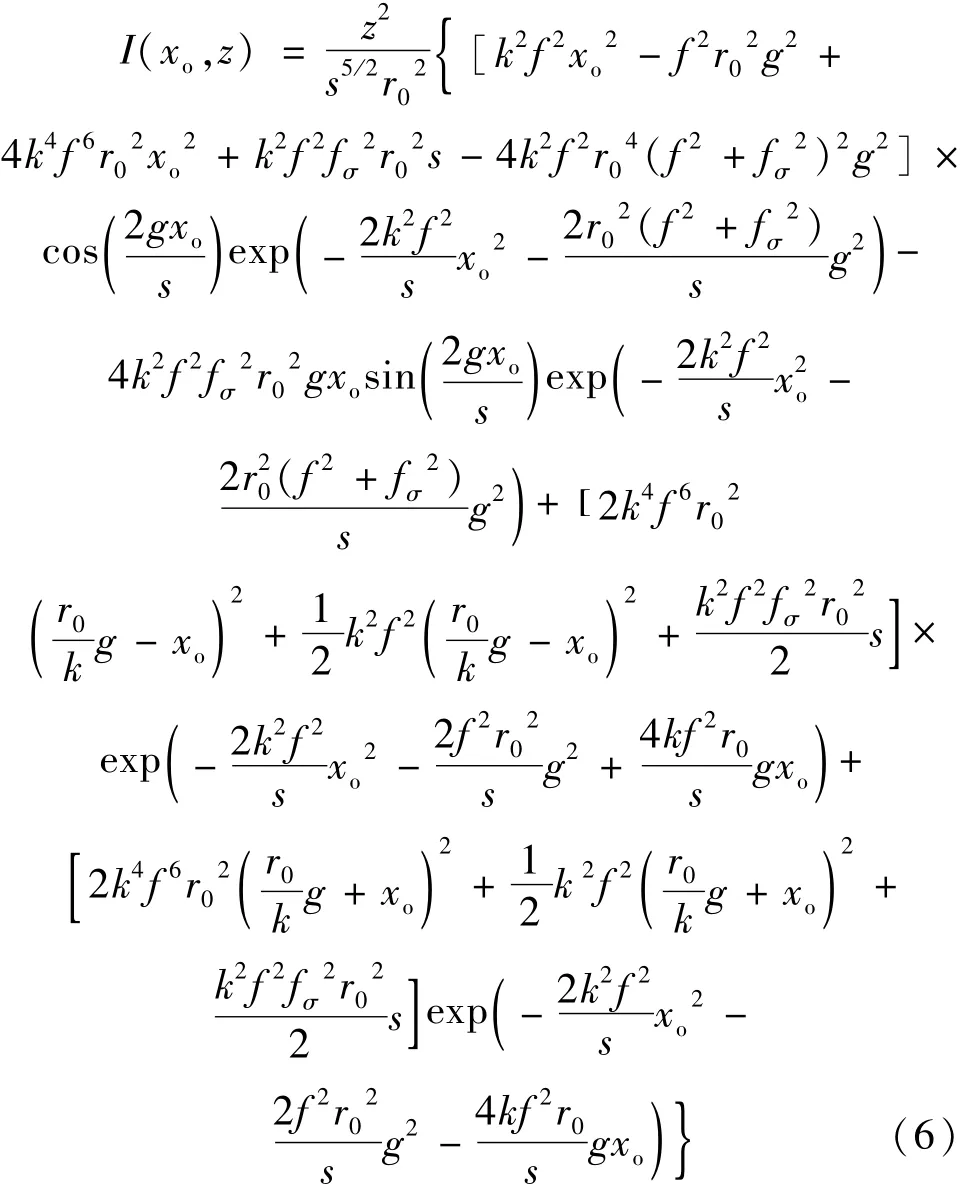
式中,s的表达式如下:
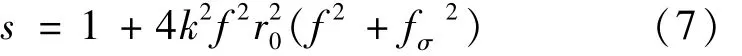
(6)式中,当g=0时,得到的是非傍轴部分相干厄米-高斯光束:
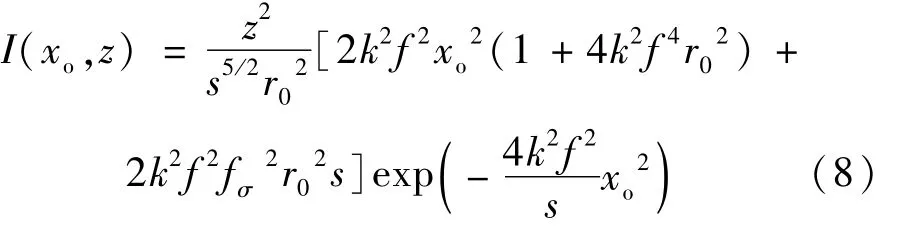
(8)式中的s同(7)式,且该式与参考文献[9]中的传输表达式(3)式一致。(6)式中,当r0≈z时,得到傍轴情况下部分相干TEM10厄米-余弦-高斯光束光强分布:
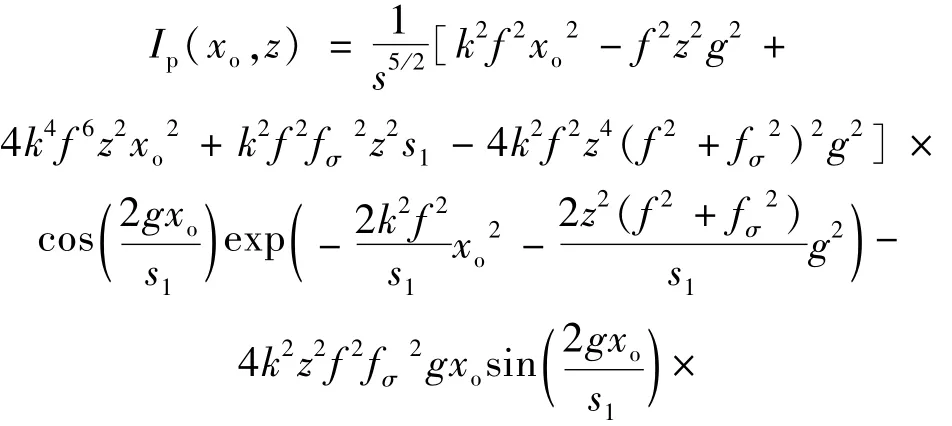

式中,s1的表达式如下:
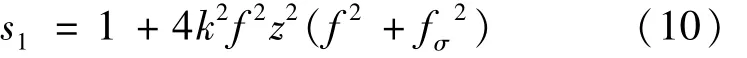
当g=0时,得到傍轴情况下TEM10厄米-高斯光束光强分布:
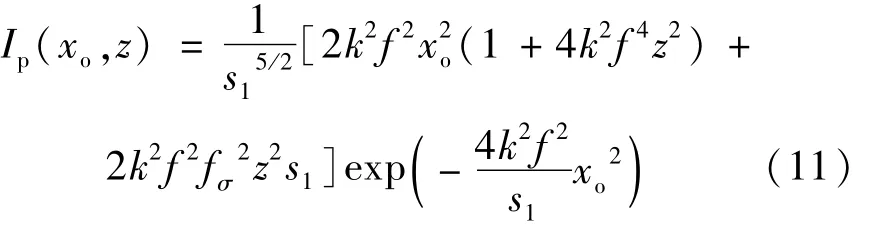
(11)式中s1与(10)式相同,且该式与参考文献[10]中的结论一致。
2 数值计算与计算机仿真
(1)当g=1时,在为瑞利长度,其中λ=1μm)平面上,两个参量f和fσ对非傍轴性的影响如图1所示。
图1中是在z=z0平面上,当参量g=1固定时,f和fσ从小变大时的归一化光强分布图,其中纵坐标为归一化无量纲,I(x,)是在z=时的光强分布,Ir是该光强的系数部分;同理,I(x,10z0)是在传输距离z=10z0平面上的光强,Ir是该光强的系数部分,横坐标一律采用(没有单位)。从图1a可以看出,当f=0.01,fσ=0.01时,傍轴与非傍轴时的归一化光强曲线是完全重合的,此时非傍轴部分相干TEM10厄米-余弦-高斯光束的特性可以用傍轴近似来分析;但从图1b可以看出,当f=0.01,fσ=0.22时,傍轴与非傍轴光强曲线开始出现偏离,即当f=0.01,fσ>0.22时,非傍轴与傍轴偏差较大,傍轴近似已不能很好地说明非傍轴光束的特性,傍轴近似无效,非傍轴近似是必须的;图1c是f=0.06,fσ=0.01时,傍轴与非傍轴归一化光强分布曲线开始出现偏差,当f>0.06时两光强曲线已相差甚远,此时傍轴近似无效,非傍轴近似是必须的。所以,从图1的3幅图得出的结论是,当g=1时,f>0.06,fσ>0.22时,非傍轴部分相干TEM10厄米-余弦-高斯光束必须被采用。
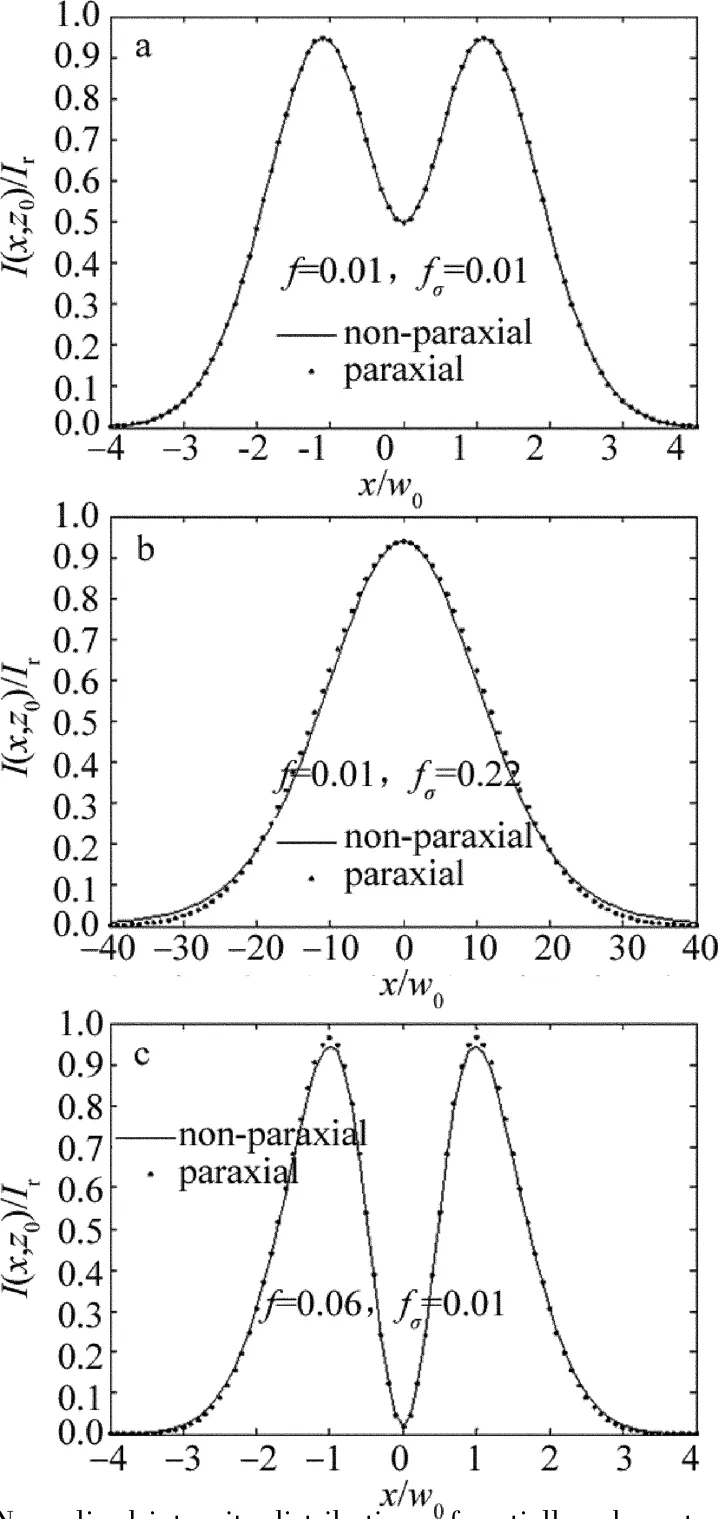
Fig.1 Normalized intensity distributions of partially coherentnonparaxial TEM10HCsG beams propagating at the plane z=z0for different values of fσand f in free space
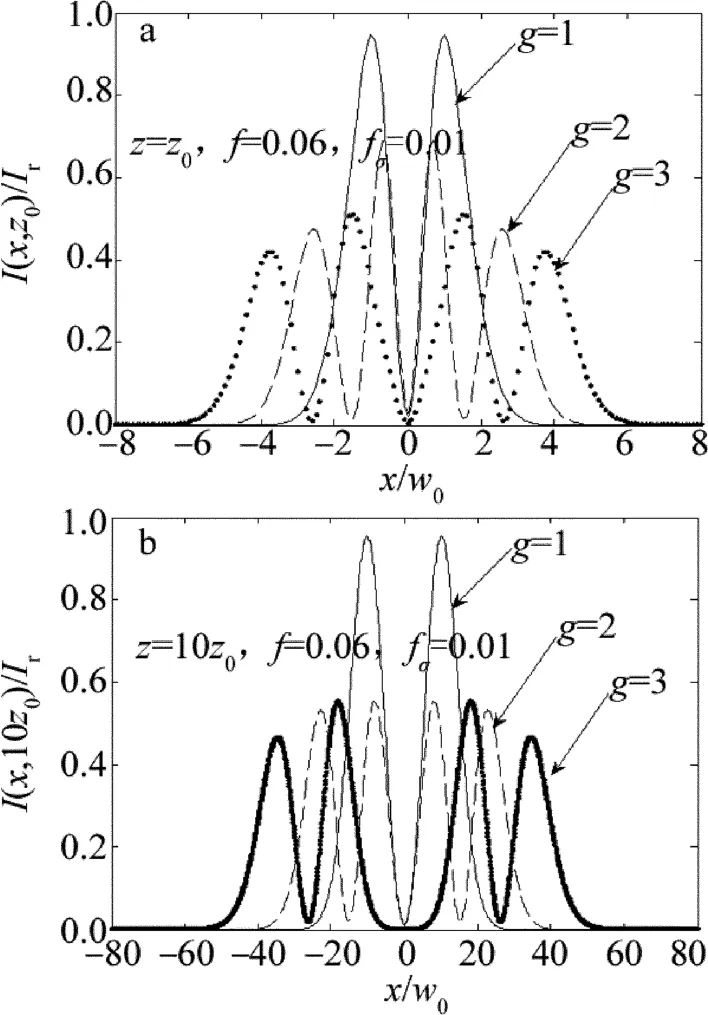
Fig.2 Normalized intensity distribution with the change of the modulation parameter of TEM10Hermite-cosine-Gaussian beams propagating in free space
(2)当f=0.06,fσ=0.01固定不变,随着传输距离的增大,通过改变调制参量g来分析归一化光强分布曲线,如图2所示。
图2中的纵横坐标的含义同图1,说明了当参量f,fσ不变,g分别为1,2,3条件下,非傍轴部分相干TEM10厄米-余弦-高斯光束在自由空间传输时,从z=z0到z=10z0平面上的归一化光强曲线不能保持其形状不变,而是随着调制参量和传输距离的增大,光强分布外移。
3 小 结
运用Wigner分布函数法,对1阶厄米-余弦-高斯光束在自由空间的传输特性进行了研究,并给出了该光束在自由空间传输时的Wigner分布函数的解析公式,在调制参量g不变的情况下,通过参量f和fσ的改变,对傍轴和非傍轴的归一化光强分布进行了对比分析,得出f=0.01(较小时),fσ<0.22时傍轴近似可以代替非傍轴近似来分析非傍轴部分相干TEM10厄米-余弦-高斯光束的特性;当f=0.01(较小时)不变,fσ<0.06时,傍轴近似是有效的;其它情况,傍轴近似无效,非傍轴近似是必须的。
另外,当参量f和fσ固定不变时,非傍轴部分相干TEM10厄米-余弦-高斯光束在自由空间传输过程中,随着调制参量g和传输距离的增大,其归一化光强分布形状不再固定,且光强分布外移,这与非傍轴厄米-余弦-高斯光束的特性[11]是一样的,而与非傍轴部分相干厄米-高斯光束的特性[12]是不一样的,说明该光束在传输过程中受束腰参量f和相干参量fσ及调制参量g的影响很大。
[1] WU Zh,YE Y X,ZHANG Y K,et al.Study on propagation properties of flattened Gaussian beam through a beam expander[J].Laser Technology,2011,35(6):861-864(in Chinese).
[2] WANG L,SHEN X J,ZHANGW A,et al.Analysis of spectral propagating properties of Gaussian beam[J].Laser Technology,2012,36(5):700-703(in Chinese).
[3] DUAN K L,LÜB D.Partially coherent non-paraxial beams[J].Optical Letters,2004,29(8):800-802.
[4] YUAN Y S,CAIY J,HALIL T,et al.Propagation factor of partially coherent flat-topped beam array in free space and turbulent atmosphere systems[J].Optics and Lasers in Engineering,2012,50(5):752-759.
[5] BASTIAANSM J.Wigner distribution function applied to partially coherent light[J].Journal of the Optical Society of America,1993,A10(1):65-87.
[6] ZHANG Y C.Propagating theory of nonparaxial beams and its application[D].Chengdu:Sichuan University,2005:27-28(in Chinese).
[7] KUANG A H,YANGH J.Partially coherentnon-paraxial vectorial Hermite-Gaussian beams and their far-field properities[J].Optik-International Journal for Light and Electron Optics,2010,121(19):1799-1801.
[8] ZHANG Y C,LÜB D.Propagation of the Wigner distribution function for partially coherent non-paraxial beams[J].Optical Letters,2004,29(23):2710-2712.
[9] KUANG A H,YANG H J.Simulation of nonparaxial partially coherent beam transmission[J].Experiment Science&Technology,2007,12(6):16-19(in Chinese).
[10] QIU Y L,GUO H,CHEN Z X.Paraxial propagation of partially coherent Hermite-Gaussian beams[J].Optical Communication,2005,245(1):21-26.
[11] WANG Q X,LÜB D.Popagation charictor of Hermite-cosine-Gaussian beams[J].High Power Laser and Particle Beams,2003,15(6):551-554(in chinese).
[12] GAO Z H,LÜB D.Partially coherent non-paraxial Hermite-Gaussian beams and their propagation properties[J].Optik-International Journal for Light and Electron Optics,2007,118(7):307-314.
Propagation characteristics of non-paraxial partially coherent Hermite-cosine-Gaussian beam s
LI Ping1,KUANG Aihua2
(1.College of Information Engineering,Huanghuai University,Zhumadian 463000,China;2.School of Electronics and Information Engineering of Zhengzhou,Zhengzhou 450007,China)
In order to study transmission characteristics of non-paraxial partially coherent Hermitian-cosine-Gaussian beam,the Wigner distribution function was used to analyze the characteristics in spatial and time domain.Their analytical propagation expressions with the three parameters of f,fσ,g were obtained for describing the space domain and frequency domain at the same time.The calculated results show that f and fσplay key roles in determining the non-paraxiality partially coherent Hermite-cosine-Gaussian beams,when g is constant.On the other hand,when g is changing,it can not preserve their shape while propagating in free space.
laser optics;non-paraxial partially coherent Hermite-cosine-Gaussian beam;Wigner distribution function;propagation expression
TN241
A
10.7510/jgjs.issn.1001-3806.2014.01.031
1001-3806(2014)01-0141-04
河南省科技攻关计划资助项目(13210 2210479);河南省科技厅重点科技攻关计划资助项目(122102210027)
李 平(1976-),女,硕士,讲师,主要研究方向为激光传输及通信。
E-mail:393423675@qq.com
2013-03-06;
2013-04-11
