基于系统动力学的交叉口通行能力测算模型的仿真与分析

杜春燕， 周溪召， 智路平

（上海海事大学经济管理学院，上海 201306）

基于系统动力学的交叉口通行能力测算模型的仿真与分析

杜春燕， 周溪召， 智路平

（上海海事大学经济管理学院，上海 201306）

交叉口作为车辆汇集、转向和疏散的枢纽，是一个复杂的动态系统，影响其通行能力的因素众多.为直观反映系统参数变化对交叉口的影响趋势，采用系统动力学方法，在分析交叉口各因素相互关系的基础上，构建了影响交叉口通行能力的各元素的因果关系图和系统流图，建立了交叉口通行能力的测算模型，并利用Vensim软件进行仿真.仿真结果显示，进口道宽度、交叉口有序度和行驶速度是影响交叉口通行能力的主要因素，可从这3个方面着手以提升交叉口通行能力.其中，控制交叉口行驶速度可成为新的交叉口扩容途径.

交叉口；通行能力；系统动力学；模型

城市路网中，交叉口是车辆与行人汇集、转向和疏散的必经之地，是城市交通的咽喉［1］.不同流向、不同行驶特性、不同类型的机动车流和行人流在此反复地合流、分流、交叉，交通运行状况极其复杂，使得道路交叉口成为制约城市路网功能发挥的瓶颈.交叉口通行能力是指交叉口某断面处，单位时间内可能通过的最大交通实体数，亦称交叉口容量.其中，交通实体多指小汽车，当有其它车辆或行人混入时，可按照相关系数进行折算.研究表明，通常情况下，平面交叉口通行能力不足路段通行能力的50%［1-6］.车辆通过平面交叉口所消耗的时间约占全程时间的40%，而交叉口延误更占了全程延误的90%左右.可见，对城市道路交叉口通行能力的研究，是提升交叉口、路网，以致整个城市综合交通系统功能的关键.

Dawkins［7］研究了具有高流率特征的停车控制交叉口车辆的驶离车头时距、排队时间等因素，并提出了相应的调整系数；Akcelik［8］研究了短车道下交叉口通行能力的测算方法，采用固定指标判断短车道效应是否发生，但未考虑交通流的实际到达情况；Wu［9-10］基于交通流向的通行能力测算模型，结合转向车流等影响因素，提出了基于流向的交叉口通行能力测算方法；高海龙等［11］结合中国典型地区的特征，给出了我国公路无信号交叉口临界间隙和随车时距的计算方法，并给出了推荐值；蒋大治［12］提出冲突度和冲突系数的概念来反映不同的交叉口控制方式对交叉口通行能力的影响；包渊秋等［13］考虑了冲突流、冲突相位及非机动车交通等因素，对不同转向车流和不同交叉口类型建立了交叉口延误函数，以增强交通分配的可靠度；王炜［14］提出了道路交叉口通行能力测算的延误分析方法，该方法将延误作为划分交叉口服务水平的标准来确定不同服务水平下的交叉口通行能力，成为交叉口规划、设计和评价的依据.

现阶段对交叉口通行能力方面的研究主要集中在分析交叉口通行能力的影响因素以及这些因素对于交叉口通行能力的影响程度、探索不同类型交叉口通行能力的计算方法、对不同交通组织形式下交叉口的通行能力进行分析、构建交叉口通行能力的综合评价体系、寻找提高交叉口通行能力的各种途径等方面，而建立模型并利用软件对交叉口通行能力进行仿真，通过改变某些参数动态直观地反映交叉口通行能力的变化趋势这方面的研究还比较少.本文在已有的交叉口通行能力综合计算方法的基础上，采用系统动力学方法建立交叉口通行能力测算模型，分析影响交叉口通行能力各个因素的影响程度，期望能够对今后研究交叉口通行能力有一定的借鉴意义.

系统动力学是分析研究信息反馈系统的一门科学，吸收了信息论和控制论的精髓，实现了与计算机仿真技术的紧密结合，是管理科学和系统科学的一个重要分支.系统动力学将系统看成一个具有多重信息的因果反馈机制，在经过剖析系统，获得丰富的信息之后，建立系统的因果关系反馈图，再转变为系统流图，从而建立起系统动力学模型，最后通过仿真语言和仿真软件对系统动力学模型进行计算机模拟，以对真实系统的结构进行剖析.交叉口通行能力是个复杂的、动态的系统，不仅与交叉口的设计结构直接相关，还与交通需求量、交通组织形式等以及一些不确定的因素密切相关.这些因素相互作用，使得交叉口的实际通行能力发生动态变化，可以从系统的角度，运用系统动力学的方法对其进行定量定性分析.

1 交叉口通行能力的系统动力学模型的建立

建立交叉口通行能力的系统动力学模型主要包括4个方面：系统边界的确定、因果关系分析、系统流图分析和方程的建立.

1.1 确定系统边界

系统边界的确定主要取决于所研究的变量和相应的时间跨度.本文的研究对象是交叉口通行能力，因此，系统的边界只涉及与之相关的实体：交叉口以及构成交叉口的路段、环岛或信号灯等交通组织工具、通过交叉口的车辆、驾驶员.本文研究的是上述实体间的关系以及相互作用所构成的系统，不考虑其它可能对整个交叉口通行能力系统产生影响的因素.

1.2 因果关系分析

交叉口通行能力系统是一个动态的复杂系统，其影响因素众多，不同层次的要素与影响因素相互制约、相互促进，任何一个环节的变动都可能对交叉口的通行能力甚至整个路网的效率产生影响.因此，在建模过程中，力图抓住主要矛盾，使模型简明扼要又符合实际.

通过分析交叉口通行能力可靠度系统中各要素间的相互关系，构建了交叉口通行能力可靠度的因果关系图（图1）.图1总共包含9条反馈回路，各个反馈回路交叉、部分重叠.其中，有3条正反馈回路，即交叉口通行能力交叉口通行能力可靠度有序度交叉口通行能力；交叉口通行能力交叉口通行能力可靠度主路车道数交叉口通行能力；交叉口通行能力交叉口通行能力可靠度路车道数交叉口通行能力.从这3条正反馈回路可知，有序度和车道数直接作用于交叉口通行能力，其变化直接影响交叉口通行能力的大小，所以，这2个状态变量是调控交叉口通行能力的主要因子.其余6条反馈回路的极性具有不确定性，之所以没有确定的极性，是因为主／支路行驶速度不仅直接作用于其路段的通行能力，同时也与路段直行车流中车辆最小车头间距有正相关关系.一方面，当路段直行车流中车辆最小车头间距处于稳定状态时，行驶速度越快，交叉口通行能力越大；另一方面，若保持高速行驶，则路段直行车流中车辆最小车头间距变大，使得交叉口通行能力相应地减小，故调整车辆行驶速度来提高交叉口通行能力要视具体的交叉口情况而定.行驶速度对整个交叉口通行能力系统影响的复杂性决定了它也是作用于该系统的主要因子，并且这些主要因子应该成为模型仿真的主要调控对象.

图1 系统模型因果关系简要流图Fig.1 Causality diagram of system model

1.3 系统流图分析

系统流图是在因果关系图的基础上，进一步区分变量的性质，更具体、更直观地刻画系统各要素之间的逻辑关系，为进一步研究系统奠定基础的图形表示方法.其图形所承载的信息远远大于因果关系图和文字的叙述，更具逻辑性，更直观，更准确.根据所建立的因果关系图，对各反馈机制进行分析，适当引入交叉口通行能力模型所需的其它变量，构建了交叉口通行能力的系统动力学流图（见下页图2）. 图2反映了交叉通行能力主要由3个部分组成：主路通行能力、支路通行能力和影响系数.路段通行能力主要是通过车道数、行驶速度、直行车流中车辆最小车头间距以及相应的影响系数导出的.其中，直行车流中车辆最小车头间距包括车辆长度、两车间最小的安全静止距离、驾驶员反应车距和制动车距这4个部分.驾驶员反应车距和制动车距都受行车速度的影响，驾驶员制动车距的构成相对复杂，涉及到道路附着系数、道路坡度、前／后车制动系数这4个因素.道路附着系数相当于轮胎与路面之间的静摩擦系数，道路附着系数越大，车胎不易打滑，行驶安全；反之，行驶缓慢.

1.4 建立方程

根据交叉口通行能力的系统动力学流图构建模型方程.交叉口通行能力的计算方程式为

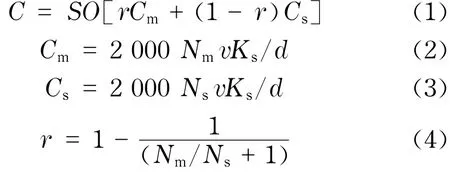
v=RAMP（1.2，0，100），即在0～100 min这个时间段内，设定行驶速度以1.2的斜率上升.

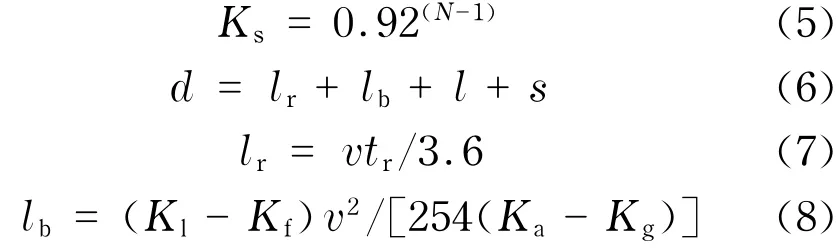
式中，C，Cm，Cs分别表示交叉口通行能力、主路理论最大通行能力、支路理论最大通行能力；N，Nm，Ns表示路段、主路和支路的单方向车道数；r为主支路通车时间分配比；lr，lb，tr表示驾驶员反应车距、驾驶员制动车距、驾驶员反应时间；v，l，s，d为行驶速度、车辆长度、两车间最小的静止安全距离、直行车流中车辆最小车头间距；Kl，Kf，Ka，Kg，Ks分别表示后车制动系数、前车制动系数、道路附着系数、道路坡度、同向车影响系数；S，O为系统损失率、有序度.

图2 交叉口通行能力的系统动力学流图Fig.2 System dynamics flow diagram of intersection traffic capacity

2 模型仿真与分析

Vensim是一个可视化的建模软件，可以描述系统动力学模型的结构，模拟系统的运行，并对模型模拟的结果进行分析和优化，在系统动力学仿真中运用广泛.本文以系统动力学软件Vensim PLE 5.11A为平台建模和仿真.

现确定模型的参数值.研究表明，驾驶员的反应时间介于0.4～1.0 s，本文取其上限，设定驾驶员反应时间为1.0 s；根据文献［15］，后车与前车制动系数之差取值范围为0.60～0.70，一般取0.67；受天气影响，沥青和水泥道路的附着系数会在0.4～0.7之间发生变化，道路附着系数取中值0.55；并设道路坡度为0，车辆长度为5 m，两车间最小的静止安全距离为2 m，支路单方向车道数为2，系统损失率为0.98.为了确定不同类型交叉口的有序度值，笔者对上海金山地区高峰时间段不同类型的交叉口车流量进行了调研，高峰时间段的车流量比较接近于实际通行能力，将它与该交叉口的理论通行能力相比，可得出该交叉口的有序度，其计算结果如表1所示.由此假设无信号控制交叉口有序度为0.40，信号控制交叉口有序度为0.60，环岛交叉口有序度为0.45.由于本文研究的是交叉口设计通行能力，因此，与时间的关系不紧密，但时间可反映不同时间段车辆行驶速度、交叉口通行能力的变化趋势，故设定时间边界为0～100，时间单位为min，步长为10 min，进行仿真模拟.

根据控制变量原则，以交叉口的通行能力为应变量，本文设定了2种调控方案，通过多次调整自变量的大小，对交叉口通行能力变化趋势进行判定和分析，从而给出合理的建议.

方案1 确定交叉口的有序度，将主路单方向车道数作2，4，6，8这4次调整.该方案的仿真结果如图3～5所示.通行能力C的单位为辆／h（veh／h）.

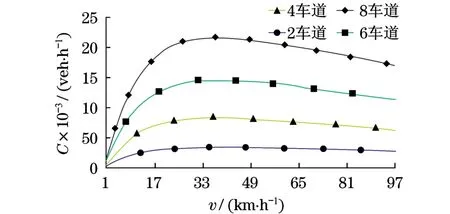
图3 信号控制交叉口下主路车道变化引起的交叉口通行能力变化Fig.3 Change of traffic capacity caused by lanes in signal control intersection

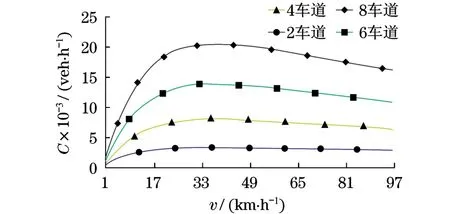
图4 环岛交叉口下主路车道变化引起的交叉口通行能力变化Fig.4 Change of traffic capacity caused by lanes in roundabout intersection

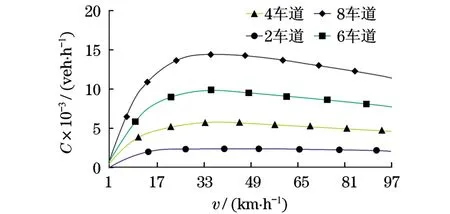
图5 无信号控制交叉口下主路车道变化引起的交叉口通行能力变化Fig.5 Change of traffic capacity caused by lanes in non-signalized intersection

对比图3～5，易发现相同车道数下，交叉口通行能力与有序度成正比，且不同有序度的交叉口的通行能力变化趋势相同.例如，当主路为单方向2车道时，无信号控制交叉口和环岛交叉口行驶速度达到24 km／h时的交叉口通行能力分别为2 107， 2 371辆；速度达到38 km／h时的交叉口通行能力分别为2 239，2 519辆；速度达到100 km／h时的交叉口通行能力分别为1744，1961辆，2107∶2371= 2 239∶2 519=1 744∶1 961=0.89.可见，模型中保证其它因素不变的情况下，调节交叉口的有序度会使交叉口通行能力成比例性变化.所以，采用合理的交叉口交通组织形式，尽可能地提高交叉口的有序度，不失为提升交叉口通行能力的有效措施.

在相同有序度下，路段车道数的增多会使得交叉口的通行能力增大，其增幅呈递减的趋势.以图4为例，行驶速度在0～38 km／h时，不同车道数的交叉口通行能力都处于上升趋势，车道数越多，通行能力上升率越大，但在0～12，12～24，24～38 km／h 这3个速度区间的增幅逐渐减小；当行驶速度超过38 km／h时，交叉口通行能力开始下降，和通行能力上升率一样，车道数越多，通行能力下降速度越快，并且随着行驶速度的提升，增加车道数所带来的通行能力优势越来越不明显.因此，单纯地依靠增加路段的宽度来提升交叉口的通行能力，其瓶颈作用非常明显，受到车辆行驶速度的制约，对交叉口通行能力的贡献值很难把控，难以达到预期的效果.并且，在城市道路网中，大部分路段两边的土地资源都已经被占用，通过拓宽道路来增加车道数量以实现交叉口的扩容已无可能，该措施也不符合资源占用最小化这一可持续发展指标的要求.

假设交叉口高峰时间段的最大车流量为8 000辆，通过交叉口的行车速度为20～40 km／h，为了实现较高的交叉口通行能力可靠度，从图3～5中可知，若有序度为0.60，主路单方向需6车道以上；若有序度为0.45，主路单方向需8车道以上；而交叉口的有序度更低时，则需要更多的车道.可见，通过增加车道来提升交叉口通行能力可靠度是不现实的，那么，设定主路为单方向4车道，当交叉口的有序度达到0.60以上时，交叉口的通行能力相对可靠.随着行驶车速的变化，交叉口通行能力波动明显，并且均在行驶车速达到38 km／h时达到最大值.这是否意味着38 km／h就是适用于所有交叉口的最佳速度，这还有待于进一步的研究，但不可否认，行驶车速确实对交叉口的通行能力具有较大的影响.

方案2 假设交叉口是信号控制交叉口，即有序度为0.60，主／支路均为单方向2车道，其它条件不变，将主／支路的道路附着系数作0.4和0.7这两次调整.

道路附着系数为0.40，0.55，0.70的速度与通行能力关系的仿真结果如表2所示.

表2 速度与通行能力关系的仿真结果Tab.2 Relationship between speed and capacity

从对方案1的分析中可知，有些交叉口的通行能力以及可靠度的提升，就需要增加多条车道数或进一步提高交叉口的有序度，这2种措施操作起来都有一定的难度.而行车速度的控制则容易得多，并且在本文的系统模型环境下，当行驶速度刚好达到38 km／h时，交叉口的通行能力最大.这个速度是否适用于所有的交叉口环境，在方案2中可以得到检验.对模型的系统流图进行分析，找出了可能影响车辆行驶速度的2个因素：道路附着系数和路段坡度，对其中的道路附着系数进行模型仿真.

将表2的每一列进行比较，不难发现行驶速度与交叉口通行能力之间的变化关系与图3～5的变化趋势大体相同，即行驶速度控制在一定范围内时，交叉口通行能力会随行驶速度的提升而上升；当行驶速度过了该范围的上界，交叉口通行能力会随行驶速度的提升而下降.分析表2的每一行可知，当车辆行驶速度相同时，道路附着系数越大，交叉口的通行能力就越大.当道路附着系数为0.40时，若车辆行驶速度为32 km／h，可以得到最大的交叉口通行能力；当道路附着系数为0.55时，若车辆行驶速度为38 km／h，得到最大的交叉口通行能力；而当道路附着系数为0.70时，行驶速度要达到44 km／h才能实现交叉口通行能力的最大化.因此，最优的通过交叉口的速度并不是固定的，要根据实际交叉口影响车辆行驶速度的相关系数分别作出调整.

近几年来，专家们在交叉口通行能力方面作了大量的研究，提出了很多提升交叉口通行能力的方法.例如，对交叉口进行渠化、增加信号控制设备、改变环岛的直径等，这些方法主要是通过提升交叉口的有序度来实现扩大交叉口通行能力的目的，具有现实的可行性.但交叉口有序的程度毕竟有限，要解决如何提升一个有序的交叉口的通行能力的问题就必须采取其它措施.通过对图3～5和表2的分析，可以发现，车辆通过交叉口的行驶速度是影响交叉口通行能力的一个重要因素.根据交叉口的实际情况以及相应的交通需求，计算出基于交叉口通行能力最大化的行驶速度范围，应该可以改善交叉口的通行状况.为了保证车辆以合理的速度通过交叉口，应考虑适当延长停车线与交叉口的距离，以满足行驶速度的要求.在交叉口树立醒目的行驶速度提示标牌，并配以相应的信号控制和法律法规强制措施，确保行驶速度在规定范围内通过交叉口，实现交叉口通行能力的优化.

3 结束语

利用系统动力学方法对交叉口通行能力的测算模型进行仿真，这是一个动态的过程.由于交叉口通行能力系统的复杂性、实际交叉口的差异性和车辆的流动性，模型中的调控参数也会动态变化.因此，测算的数据仅代表系统内部因素之间的相关关系和实际交叉口通行能力的变化趋势，不能完全反映现实各交叉口系统的现状.要使该模型更具参考价值，必须考虑更多的影响因素，对系统参数依据实际状况进行细分并不断调整，增强其科学性、实用性.

仿真结果表明，可以从道路宽度、交叉口有序度和车辆行驶速度这3个方面来提升交叉口的通行能力.拓宽道路宽度、增加车道数，受到道路网周边开发利用状况的制约，不符合可持续发展的要求，并且相对于其它手段而言成本较高、耗时较长、适用性较低.提升交叉口有序度是目前普遍采用的措施，但是，如今道路规划越来越成熟，道路信息系统也日趋完善，交叉口的有序度普遍提高，在这样的情况下，力图通过继续提升有序度来实现扩容的目标，效果很有限.而根据实际交叉口的状况和交通需求，设置合理的行驶速度范围来增加交叉口的通行能力，不失为一个新的可行的选择.交叉口作为方向转换枢纽，在方向转换的过程中，原来直行稳定的车流会受到许多因素的干扰而成为一个不稳定的车流，如何在这样的不稳定性中将行驶速度稳定在一定的区间内，是施行该措施面临的首要问题，这还有待于进一步的研究.

［1］ 吴潜蛟，罗向龙，武奇生，等.车辆排队间距对交叉口通行能力的影响［J］.公路交通科技，2009，26（12）：112-115.

［2］ 纪凯.平面交叉口信号控制方法研究与仿真设计［D］.南京：东南大学，2004.

［3］ 徐良杰.单点交叉口信号协调优化控制技术研究［D］.南京：东南大学，2005.

［4］ 张国华.信号交叉口设计及微观仿真研究［D］.北京：北方交通大学，2000.

［5］ 李美玲.信号交叉口交通组织优化方法研究［D］.北京：北京工业大学，2004.

［6］ 程国柱.路口拓宽条件下信号交叉口通行能力研究［D］.哈尔滨：哈尔滨工业大学，2002.

［7］ Dawkins J M.Analysis of stop-controlled intersections in the Caribbean：a case study of Kingston，Jamaica ［D］.Atlanta：Georgia Institute of Technology，1997.

［8］ Akcelik R.Traffic signals capacity and timing analysis ［R］.Sydney：Australia Road Research Board，1981.

［9］ Wu N.Determination of capacity at all-way stopcontrolled intersections［J］.Transportation Research Record，2000（1710）：205-214.

［10］ Wu N.Total capacities at all-way stop-controlled intersections：validation and comparison of“highway capacity manual”procedure and addition-conflict-flow technique［J］.Transportation Research Record，2002 （1802）：54-61.

［11］ 高海龙，王炜，刘秉轩，等.中国典型地区无信号交叉口临界间隙调查［J］.东南大学学报（自然科学版），2000，30（3）：100-103.

［12］ 蒋大治.城市道路交叉口通行能力实用分析方法研究与软件开发［D］.南京：东南大学，2003.

［13］ 包渊秋，严凌.面向交通规划的交叉口延误函数的研究和应用［J］.上海理工大学学报，2005，27（3）：253-258.

［14］ 王炜.道路平面交叉口通行能力的延误分析法［J］.中国公路学报，1998，11（增刊）：62-67.

［15］ 杨福广，李贻斌，阮久宏，等.基于扩张状态观测器的路面附着系数实时估计［J］.农业机械学报，2010，41 （8）：6-9.

（编辑：石 瑛）

Simulation and Analysis on Intersection Capacity Based on System Dynamics

DUChun-yan， ZHOU Xi-zhao， ZHILu-ping
（School of Economics&Management，Shanghai Maritime University，Shanghai 201306，China）

Intersection as a hub for vehicles to collect，stee and evacuae，is a complex dynamic system，and many factors affect its capacity.System dynamics method was selected to visualize the trends when system parameters changing on the intersection.The causal loop diagrams，system flow diagrams and calculation model of intersection capacity were built based on the analysis of the relationship between the intersection factors.The simulation result by sung the software of Vensim shows that the width of the sections，the intersection’s degree of order and driving speed are the main influencing factors on intersection capacity.The intersection capacity can be enhanced from the above three aspects.Among them，the control of intersection speed can be a new way for improvement.

intersection；capacity；system dynamics；model

U 491文献标示码：A

1007-6735（2014）05-0449-07

10.13255／j.cnki.jusst.2014.05.008

2013-07-01

国家自然科学基金资助项目（61273042）；上海市教委科研创新资助项目（12ZZ147）；上海市科委地方院校能力建设资助项目（13510501700）；上海市大文科研究生学术新人培育计划资助项目（wk2013021）；上海海事大学研究生创新能力培养专项基金资助项目（2013ycx024）

杜春燕（1989-），女，硕士研究生.研究方向：交通运输规划与管理.E-mail：dcy0316＠126.com

周溪召（1964-），男，教授.研究方向：智能交通系统、交通理论与运输规划.E-mail：xizhaozhou＠163.com