地震学百科知识（八）——计算地震学＊

地震科普

地震学百科知识（八）
——计算地震学＊

王彦宾1）陈晓非2）

1）北京大学地球与空间科学学院，北京100871
2）中国科学技术大学地球与空间科学学院，合肥230026

引言

研究理论地震学计算问题所涉及的数值算法以及计算机实现是一门分支学科。它的诞生得益于计算机的广泛应用和大量的高质量地震波形观测资料的获得，是介于理论地震学、计算科学和观测地震学之间的新兴交叉学科。

基于基本的物理定律和严格的数学工具，理论地震学给出了定量描述地震震源自发破裂动力学过程、地震波激发、地震波传播等问题的控制方程。但是，这些方程只对极少数相对简单的地球模型能够给出完整的解析解。随着全球范围内地震观测资料数量的增多和覆盖区域的扩大，地震学家认识到地震震源的复杂性和地球内部结构的非均匀性。对于更接近真实地球的复杂模型，控制方程不能给出解析解。随着计算机的出现和数值算法的发展，各类控制方程都可以通过数值方法快速、精确地求解，对于一些相对简单的复杂模型，可以结合数值方法给出半解析解，对于任意复杂模型，通常只能依赖数值方法给出数值近似解。

1 历史

1950—1955年间数字计算机开始引入地震学研究，带来地震学的“第二次革命”［1］。计算地震学作为一门交叉学科在这一背景下产生。Thomson［2］和Haskell［3］分别于1950年和1953年给出了水平多层介质中面波频散的数值算法，1955年Pekeris［4］首次利用计算机数值求解兰姆（H.Lamb）问题（半无限均匀弹性空间内由点源或线源激发的弹性波传播问题），给出了泊松固体介质中点源激发的理论地震图。随后，1959年实现了全球模型运动方程的数值积分计算，1959—1960年间，Dorman等［5］发表了第一个基于数值计算给出的包含低速层的海洋地幔模型，1960年利用数值方法进行了震中定位，1964年进行了复杂地球模型中面波的激发模式和地球介质Q值的反演，1965年和1969年利用快速傅里叶变换进行了傅立叶振幅谱和功率谱的数值计算。1962—1969年间，数值计算方法提高了地震数据处理能力，数字滤波、多维傅里叶变换、F－K变换（F指频率，K指波数）、时间域谱分析等技术应用于地震数据处理。此后，理论地震学中的正演计算、反演计算、数据处理越来越多地依赖于数值方法［1，6－7］。

2 基本思想

计算地震学最根本的思想是如何将连续的地球介质转化为离散的模型，然后在计算机上对离散模型实现数值求解。通常将真实地球介质在空间上划分为细小的单元，在单元的节点上通过一定的数值算法求解方程，得到连续模型的近似数值解。一般包括以下一些步骤：

（1）预处理。

①确定物理问题的控制方程；

②确定物理问题对应的真实地球介质模型的空间范围；

③将介质在空间上离散为单元；

④定义相应的初始条件和边界条件。

（2）数值计算开始，迭代（或递推）求解。

（3）计算结束，利用后处理方法分析计算结果，并用可视化技术表示结果。

3 常用方法

计算地震学中常用的数值方法可以分为域类方法（domain method）和边界类方法（boundary method）两大类。

域类方法是在整个计算模型空间区域上进行离散，用分布在整个区域上的有限个节点上函数的近似值来代替连续问题的解。常用的方法包括：

（1）有限差分方法；

（2）有限单元方法；

（3）伪谱方法；

（4）谱元方法。

有限差分法和有限单元法是应用于计算地震学较早的传统数值方法。伪谱法和谱元法则是近些年引入的新方法。伪谱方法（pseudo－spectral method）是谱方法的一种，和有限差分法类似，它只在离散节点上近似函数值，节点上函数的微分计算通过快速傅里叶（Fourier）变换或切比雪夫（Chebyshev）变换实现，因此，它具有精度较高的特点。谱元法（spectral－element method）是一种高阶有限单元方法，它选取以正交多项式表示的基函数，它吸取了谱方法精度高的优点，提高了计算精度和效率。

此外，还发展了基于以上基本方法的混合方法，以提高计算精度和效率。

不同的域类方法划分网格的方式不同，但是都能够较好地处理空间上变化较大的非均匀介质模型。

边界方法主要包括边界元、边界积分方程等方法，它将计算模型空间的边界离散化，在边界的节点上求解。它是针对域类方法占用计算机内存资源过多的缺点而发展起来的一种求解偏微分方程的数值方法，它的最大优点是降维，将三维问题降维为二维问题，二维问题降维为一维问题，只在求解区域的边界进行离散就能求得整个模型区域的解。

4 应用

计算地震学主要应用于理论地震学的正演和反演两大领域。对于给定的地球介质模型和特定的地震学问题，正演是通过数值方法求解方程，给出预测的理论解，有助于理解地震学问题的物理过程。反演则是建立在正演基础之上的数值计算，通过正演结果和地震观测数据之间的拟合，估计地球介质的地震波速度结构、介质物性参数和震源参数等，反演过程中的正演计算和反演算法都需要利用数值方法实现。在实际应用方面，目前计算地震学已经广泛用于全球、区域和局部不同尺度的地球介质速度结构和物性参数成像以及地震震源过程研究，为地球动力学研究提供证据，为勘探地震学和强震地面运动预测提供新的手段。此外，数值方法也广泛应用于地震观测数据的分析和处理中［8－11］。

王彦宾等［12］基于傅里叶伪谱法（Fourier pseudospectral method，PSM），发展了模拟具有任意横向非均匀结构的全地球模型中SH波传播的一种数值计算方法。图1给出了他们计算的一个模拟的深源地震（震源深度600km）激发出的SH波在地球中的传播情况。计算中采用的地球地震波速结构模型是PREM模型（1981由美国A.M.Dziewonski和D.L.Anderson提出的初步参考地球模型）。图1展示出震源激发地震波后4个时刻的SH波的波场快照图，从图中可看出，不同时刻SH波在各个界面上的反射、透射和绕射情况，图中还标出了在各个时刻SH波的多个震相在地球内部到达的位置。

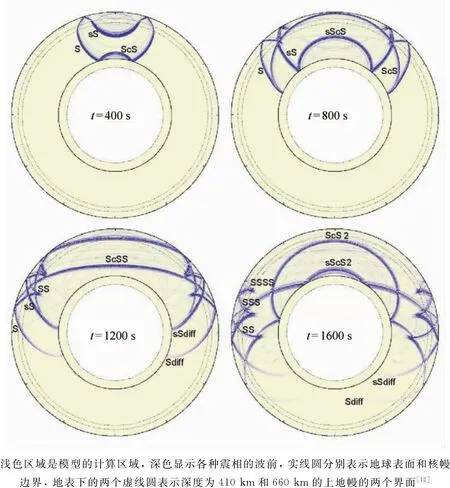
图1 用PREM模型计算得到的4个时刻的SH波位移波场快照图

5 前景

计算地震学的发展是由以下几个因素推动的：地震观测数据不断增多，人们认识到数据所反映的地球介质以及地震过程的复杂性，希望通过复杂介质模型以及地震震源过程的正演和反演修正地震学的理论，并得到更符合实际的地球模型。快速发展的计算机硬件条件和数值算法为此提供了必不可少的条件［13］。

目前，计算地震学已经能够处理三维复杂模型和模拟地震破裂的动态过程。可以预见，随着计算机性能的不断提高和数值方法的发展，计算地震学将发挥更重要的作用，通过更接近实际的地球模型的数值计算，提高我们对地震这一自然现象本质的认识，减轻地震灾害对人类的威胁，提高我们对地下自然资源的勘探能力。

作者电子信箱 王彦宾#ybwang＠pku.edu.cn$

［1］Ben－Menahem A.A concise history of mainstream seismology：origins，legacy and perspectives.Bull.Seis.Soc.Amer.，1995，85（4）：1202－1225

［2］Thomson W T.Transmission of elastic waves through a stratified solid.J.Appl.Phys.，1950，21：89－93

［3］Haskell N.The dispersion of surface waves in multilayered media.Bull.Seis.Soc.Amer.，1953，43：17－34

［4］Pekeris C L.The seismic surface pulse.Proc.Nat.Acad.Sci.USA，1955，41：469－480

［5］Dorman J，Ewing M，Oliver J.Study of shear velocity distribution in the upper mantle by mantle Rayleigh waves.Bull.Seis.Soc.Amer.，1960，50（13）：87－115

［6］Engdahl E R，Taggart J，Lobdell J L，et al.Computational methods.Bull.Seis.Soc.Amer.，1968，58（4）：1339－1344

［7］Harkrider D G.The early years of computational seismology at Caltech.Bull.Seis.Soc.Amer.，1988，78（6）：2105－2109

［8］Herrmann R B.Digital processing of regional network data.Bull.Seis.Soc.Amer.，1982，72（6B）：S261－S276

［9］Allen R.Strong motion prediction using mathematical modeling techniques.Bull.Seis.Soc.Amer.，1982，72（6B）：S29－S41

［10］Engdahl E R，Peterson J，Orsini N A.Global digital networks：current status and future directions.Bull.Seis.Soc.Amer.，1982，72（6B）：S243－S259

［11］Aki K.Strong motion prediction using mathematical modeling techniques.Bull.Seis.Soc.Amer.，1982，72（6B）：S29－S41

［12］王彦宾，Takenaka H.利用伪谱法模拟横向非均匀全球SH波场.中国科学：地球科学，2012，42（1）：140－148

［13］Tromp J.A new era in computational global seismology.Seism.Res.Lett.，2001，72（6）：640－641

P315.01；

： A；

10.3969／j.issn.0235－4975.2014.02.007

2013－12－18。