基于包含度理论的概念格构造方法研究
2014-06-23何苗,石慧,魏玲
何 苗,石 慧,魏 玲
(西北大学数学系,陕西西安 710127)
Wille R.于1982年首先提出了形式概念分析理论[1-2],用于概念的发现、排序和显示。形式背景与形式概念是形式概念分析的基本概念,形式概念是由形式背景中的对象集和属性集组成的统一体,形式概念之间可形成一种有序的层次结构——概念格,概念格的构造[3-5]是形式概念分析理论的主要研究内容之一。
Duntsch和Gediga把粗糙集中的上、下近似算子引入概念格理论中,得到了面向属性概念格[6]。类似地,Yao获得了面向对象概念格,并对两者之间的关系做了进一步的研究[7-9]。包含度理论[10]是张文修教授提出的一种定量化不确定性的理论,是对“包含关系”的扩充,从而包含了“关系”的不确定性。作者利用包含度基于形式背景定义了4种新的算子,并证明了当包含度取不同的值时,可以构造4种概念格,即经典概念格、补背景概念格、面向属性概念格和面向对象概念格。因而,本文提出的基于包含度理论构造概念格的方法可以实现对多种概念格构造方法的统一。
1 预备知识
定义1[2]称(G,M,I)为一个形式背景,其中G={g1,…,gt}为对象集,每个gi(i≤t)称为一个对象;M={m1,…,ms}为属性集,每个mj(j≤s)称为一个属性;I为G和M之间的二元关系I⊆G×M。若(g,m)∈I,则称g具有属性m,用gIm表示。
对于形式背景(G,M,I),在对象集X⊆G和属性集B⊆M上分别定义运算
X*={m|m∈M,∀g∈X,gIm},
B'={g|g∈G,∀m∈B,gIm}。
∀g∈G,记{g}*为g*;∀m∈M,记{m}'为m'。若∀g∈G,g*≠∅,g*≠G,且∀m∈M,m'≠∅,m'≠M,则称形式背景(G,M,I)是正则的。本文提到的形式背景都是正则的。
对于二元关系I,定义其补关系Ic={(g,m)|¬ (gIm)},则形式背景(G,M,Ic)是(G,M,I)的补形式背景。
设(G,M,I)是形式背景,∀A⊆G,B⊆M,若满足A*=B且A=B',则称(A,B)是一个形式概念,简称概念;其中A称为概念的外延,B称为概念的内涵。形式背景(G,M,I)的全体概念记为 L(G,M,I)。∀(A1,B1),(A2,B2)∈ L(G,M,I),定义
(A1,B1)∧ (A2,B2)=(A1∩ A2,(B1∪B2)'*),
(A1,B1)∨ (A2,B2)=((A1∪ A2)*',B1∩B2),
则L(G,M,I)是完备格,称为概念格。
定义2[6]设(G,M,I)是形式背景,∀X⊆G,B⊆M,定义一对近似算子◇,□,:
X◇={m|m∈M,m'∩X≠∅},
B□={g|g∈G,g*⊆B}。
定义3[6]设(G,M,I)是形式背景,∀X⊆G,B⊆M,若一个二元组(X,B)满足X◇=B,B□=X,称(X,B)为面向属性概念。
记 LP(G,M,I)={(X,B)|X◇=B,B□=X},则LP(G,M,I)是完备格,称为面向属性概念格。其上、下确界定义为:∀(X1,B1),(X2,B2)∈ LP(G,M,I),
(X1,B1)∧ (X2,B2)=(X1∩ X2,(B1∩B2)□◇),
(X1,B1)∨ (X2,B2)=((X1∪X2)◇□,B1∪B2)。
定义4[9]设(G,M,I)是形式背景,∀X⊆G,B⊆M,若一个二元组(X,B)满足X□=B,B◇=X,称(X,B)为面向对象概念。
记 LO(G,M,I)={(X,B)|X□=B,B◇=X},则LO(G,M,I)是完备格,称为面向对象概念格。其上、下确界定义为:∀(X1,B1),(X2,B2)∈ LO(G,M,I),
(X1,B1)∧ (X2,B2)=((X1∩X2)□◇,B1∩B2),
(X1,B1)∨ (X2,B2)=(X1∪ X2,(B1∪B2)◇□)。
定义5[11]设(G,M,I)是形式背景,∀X⊆G,B⊆M,在X和B上定义运算
X+={m∈M|∀g∈X,(g,m)∉I},
B+={g∈ G|∀m ∈B,(g,m)∉I}。
设(G,M,I)是形式背景,∀X⊆G,B⊆M,若满足X+=B且X=B+,则(X,B)是补背景(G,M,Ic)的概念。补背景(G,M,Ic)的全体概念记为L(G,M,Ic)。∀(A1,B1),(A2,B2)∈L(G,M,Ic),定义
(A1,B1)∧ (A2,B2)=(A1∩ A2,(B1∪B2)'*),
(A1,B1)∨ (A2,B2)=((A1∪A2)*',B1∩B2),
则L(G,M,Ic)是完备格,称为补背景的概念格。
2 基于包含度的4种概念格构造方法
本节主要基于包含度定义了新算子,当包含度取不同的值时,新算子就是*,',+,◇,□,算子,由此可以构造经典概念格、补背景概念格、面向对象概念格和面向属性概念格。
定义6[10]设(X,≤)是偏序集,若对于任意x,y∈X,都有数D(y/x)与之对应,且满足:
1)0≤D(y/x)≤1,
2)x≤ y⇒ D(y/x)=1,
3)x≤ y≤z⇒ D(x/z)≤ D(x/y),则称D为X上的包含度。
设G是有限集,Π(G)表示G上的全体子集,“⊆”表示集合的包含关系,则(Π(G),⊆)为偏序集。∀E∈Π(G),F∈Π(G),记则根据包含度的定义可知,D为Π(G)上的包含度。
定义7 设(G,M,I)是形式背景,∀X≠∅,X⊆G,B≠∅,B⊆M,在X和B上定义运算(0≤α≤β≤1):
定义8 设(G,M,I)是形式背景,∀X⊆G,B⊆M,在X和B上定义运算(0≤α≤β≤1):
例1 表1给出的形式背景(G,M,I)来源于匈牙利的科教电影“生物与水”[2]。这里的对象是电影中提及的生物,属性是电影所强调的特性。对象和属性代码意义如下:①蚂蝗,②鱼,③蛙,④狗,⑤水草,⑥芦苇,⑦豆,⑧玉米;a:在水中生活,b:在陆地生活,c:有叶绿素,d:双子叶,e:单子叶,f:能运动,g:有四肢,h:哺乳。
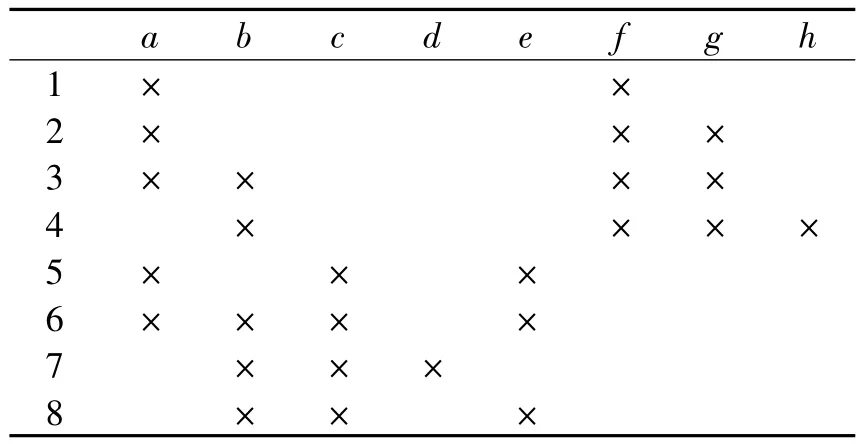
表1 科教电影“生物与水”的形式背景(G,M,I)Tab.1 Formal context(G,M,I)of science and eduration filum"Biology and Water"
考察表1的形式背景 (G,M,I)。若设 α =0.5,β=1,则根据定义7和定义8可得:
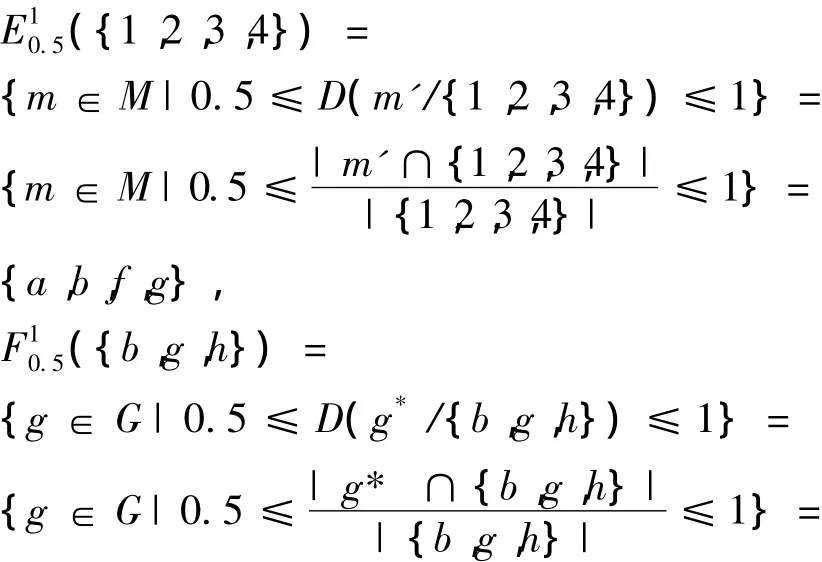
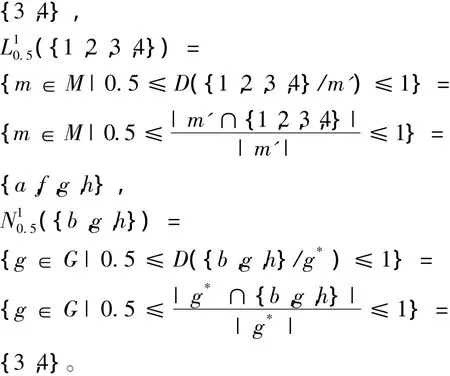
根据定义7和定义8,可得如下结论。
性质1 当[α1,β1]⊆[α2,β2]时,以下性质成立
例2 考察形式背景表1。若取[α1,β1] =[0.5,1],[α2,β2] = [0.25,1],则计算可得
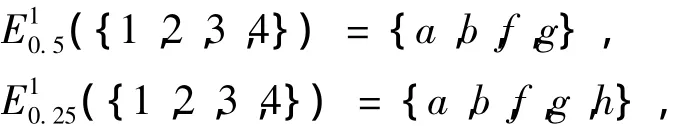
因此

因此
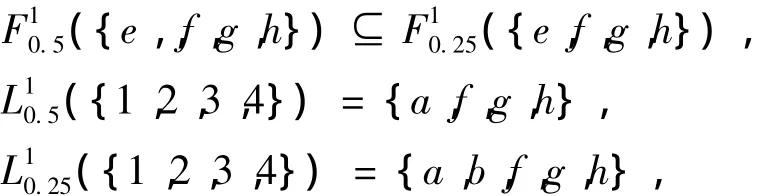
因此
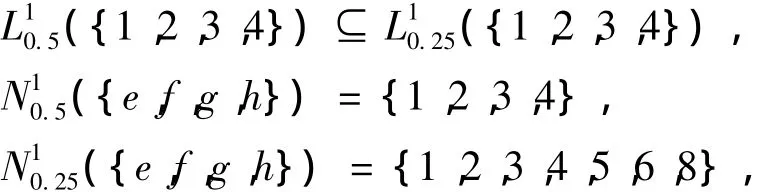
因此
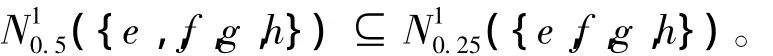
定理1 设(G,M,I)是形式背景,∀X⊆G,B⊆M,0≤α≤β≤1,有
证 明1)E11(X)={m∈M|D(m'/X)=1}=
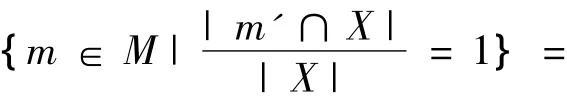
{m∈M|X⊆m'}=X*,
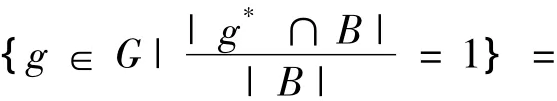
{g∈ G|B ⊆ g*}=B'。
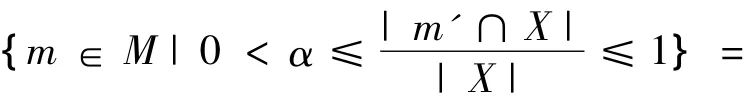
{m∈M|X∩m'≠∅}=X◇。
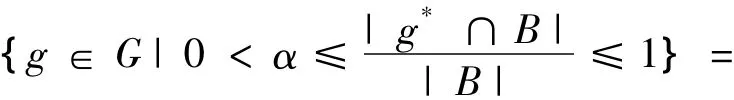
{g∈G|B∩g*≠∅}=B◇。
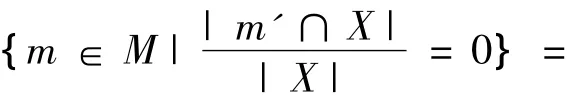
{m∈M|m'∩X=∅}=X+,
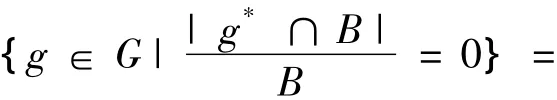
{g∈G|g*∩B=∅}=B+。
定理2 设(G,M,I)是形式背景,∀X⊆G,B⊆M,0≤α≤β≤1,有
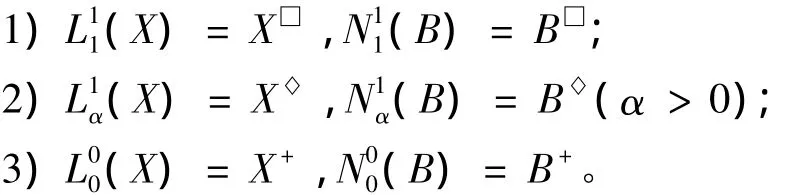
证 明1)L11(X)={m∈M|D(X/m')=1}=
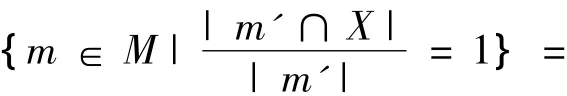
{m∈M|m'⊆X}=X□,
N11(B)={g∈G|D(B/g*)=1}=
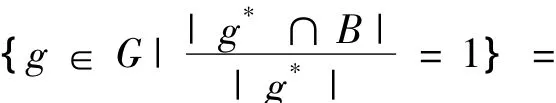
{g∈G|g*⊆B}=B□。
2)L1α(X)={m∈M|α≤D(X/m')≤1}=
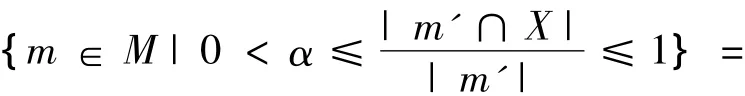
{m∈M|X∩m'≠∅}=X◇,
N1α(B)={g∈ G|α ≤ D(B/g*)≤1}=
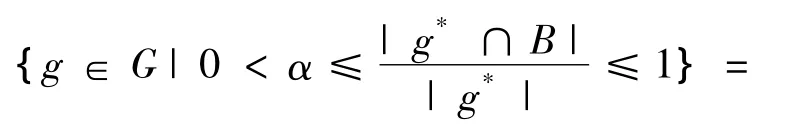
{g∈G|g*∩B≠∅}=B◇。
3)L00(X)
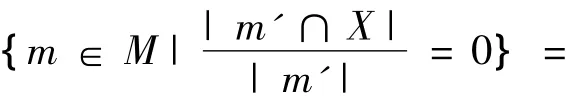
{m∈M|X∩m'=∅}=X+,
N00(B)={g∈G|D(B/g*)=0}=
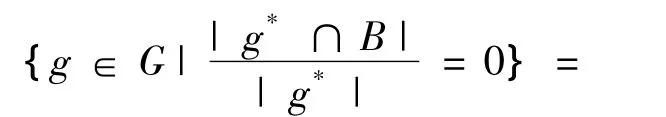
{g∈G|B∩g*=∅}=B+。
可由以上定理以及已有的*,',+,◇算子的性质[2,6,11],得出以下结论。
推论1 设(G,M,I)是形式背景,∀X1,X2,X⊆G,B1,B2,B⊆M,以下性质成立
(Ⅰ)当α=β=1时


由定理1与定理2知,当α,β取特定的值时,Eβα,Fβα算子对应着形式背景的概念格与补背景概念格中的算子,因而可以构造相应概念格。类似地,Lβα,Nβα算子对应补背景概念格、面向对象概念格与面向属性概念格中的算子,因而可以构造这3种格。具体方法如下定理所示。
定理3 设(G,M,I)是形式背景,∀X⊆G,B⊆M(0≤α≤β≤1),则
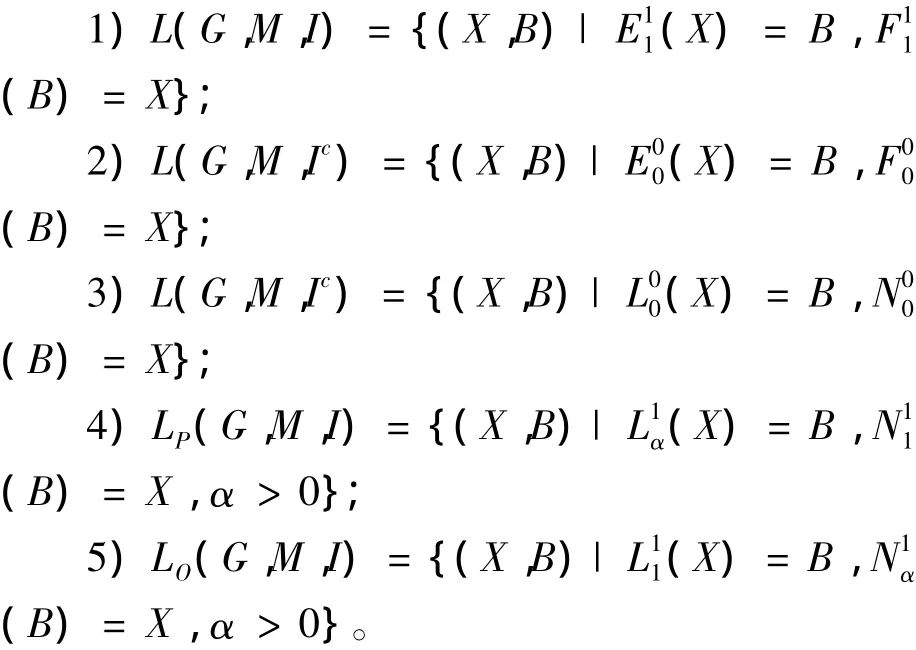
3 结语
本文基于包含度理论定义了新的算子,并证明了当包含度取不同的值时,利用新算子可以构造4种概念格,即经典概念格、补背景概念格、面向属性概念格和面向对象概念格。这种基于包含度方法是对这4种概念格构造方法的统一。
[1]WILLE R.Restructuring lattices theory:an approach based on hierarchies of concepts[C]∥RIARAL I,Ordered Sets.Dordrecht:Reidel,1982:445-470.
[2]GANTER B,WILLE R.Formal Concept Analysis[M].Mathematical Foundations,New York:Springer-Verlag,1999.
[3]CARPINETO C,ROMANO G.Concept Data Analysis:Theory and Application [M].Chichester:John Wiley&Sons,Ltd,2004.
[4]HO T B.Discovering and using knowledge from unsupervised data[J].Decision Support System,1997,21(1):29-42.
[5]BELOHLAVEK R.Fuzzy closure operators[J].Journal of Mathematical Analysis and Applications,262(2001)473-489.
[6]DUNTSCH I,GEDIGA G.Approximation operators in qualitative data analysis[C]∥In:Theory and Application of Relation of Structures as Knowledge Instruments,2003:216-233.
[7]YAO Y Y.A comparative study of formal concept analysis and rough set theory in data analysis[J].Lecture Notes in Artificial Intelligence,2004,3066:59-68.
[8]YAO Y Y.A partition model of granular computing[J].Lecture Notes in Computer Science,2004,3100:232-253.
[9]YAO Y Y.Concept Lattices in Rough Set Theory[C]∥DICK S,KURGAN L,PEDRYCZ W,et al.Proceedings of 2004 Annual Meeting of the North American Fuzzy Information Proceeding Society Washington:IEEE Computer Society,2004:796-801.
[10]张文修,梁怡.不确定性推理原理[M].西安:西安交通大学出版社,1996.
[11]何苗,魏玲.基于原背景的补背景概念获取[J].计算机科学,2012,39(11):197-200.
