基于方差系数统计的合成孔径雷达相干斑强度估计

凤宏晓 屈建社

(陕西黄河集团有限公司 西安 710043)

0 引言

相干斑是SAR成像系统本身所固有的，在不同成像系统或参数下产生的相干斑的强度也是不同的。理想情况下，对同一场景的L幅单视图像进行平均时，就会获得L视的SAR图像，此时我们也将知道相应的相干斑的方差值。但是，这需要假设多普勒带宽分割得到的子带宽之间是相互独立的，而在实际中各个子带宽之间往往存在一定的相关性［1-2］。同时，若采用空间平均的多视处理方法，由于SAR图像内部的像素之间存在很明显的空间相关性，空间独立的假设也是不能很好满足的［1］。当子带宽或空间的独立性不能满足时，在完全发展相干斑的假设下，经过多视处理所获得名义上的视数要大于其有效的视数值［2］(Effective Number of Looks)。此外，SAR图像的灰度范围发生变化［3］、图像的尺寸调整与裁剪、不同图像格式之间转换以及图像经过信道编码传输等都会对相干斑的强度产生影响。因此，对SAR图像中相干斑的有效视数的估计显得非常重要。

最早研究视数估计的学者是华人科学家Lee J.S.，在文献［4］中，他提出一种有监督的视数估计方法，但由于该方法涉及人工的操作使得估计结果存在比较大的不确定性。为了克服这个不足，Lee J.S.等［3］又提出了一种无监督的视数估计方法，但该方法依然需要依靠经验人工地选择较多个参数，如:扇形的角度、小区域的大小，并且参数值对最终的估计结果很敏感。Sathit I.等［5］也提出了一种无监督的视数估计，但是该方法只能用于强度SAR图像，并且对估计图像广义Gamma分布的假设使得估计非常复杂。

基于Lee J.S.的思想［3］，本文提出了一种新的无监督相干斑强度估计方法。首先把SAR图像划分为多个图像块，接着对每个图像块计算其方差系数，最后统计已得到的方差系数的概率密度函数，并根据概率密度函数的最大值得到最终的相干斑强度估计。相比Lee的算法［3］，本文所提算法在参数选择上更加容易，估计思想及过程非常简便，大量模拟以及真实数据的测试证明了本文所提算法的有效性。

1 基于均值—标准差平面的相干斑强度估计

在已知SAR图像视数信息的情况下，相干斑名义上的强度值可使用下面的式子计算获得:

其中，Ln代表从数据源获得的名义上的视数值。

这里先给出图像方差系数γ(Variation Coefficient)的定义［4］:

其中，f代表某种信号。

若假设信号f等于相干斑Z，考虑到SAR图像相干斑Z的均值为1，我们定义相干斑的方差系数如下:

可以看出，相干斑的方差系数实际上是和其标准差相等的。在一个同质区域内，真实的SAR图像X是一个常数X0［4］，应用SAR图像乘性模型Y=X·Z(Y表示SAR图像的观测值)，我们可得到

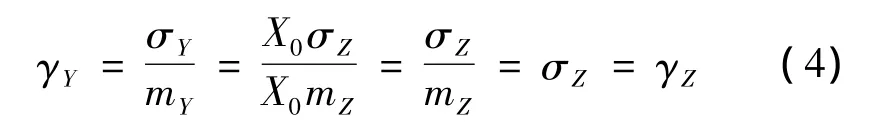
(4)式说明，在一个同质区域内，其观测图像的方差系数与相干斑的标准差是相等的，换句话说，相干斑强度的估计可以转化为同质区域内的方差系数的估计。

通常，为了计算γY，需要选择许多同质区域。接着计算每个区域的均值mY和标准差σY，并将每个块的均值与标准差作为一个点(mY，σY)加入到一个二维平面上。实际中，这些点会聚成一类，找个一条经过原点的直线，同时让该直线通过聚类中心，此时直线的斜率就是所要计算的γY，这就是Lee J.S.等在文献［4］中提到的估计方法，图1给出了这种方法的一个估计示例。由于需要人工的选择同质区域，因此这是一种有监督的估计方法。为了改进人工选择的缺陷，Lee J.S.等在文献［3］中提出了一种估计方法，其基本思路是将图像划分为一个个互不重叠的小区域，然后采用两种方法自动的估计。文献［3］中的无监督估计方法实际上是需要人工设定多个选择参数的，并且每个参数都对估计结果敏感。

图1 均值平方—方差平面估计相干斑强度示意图

2 本文算法——基于方差系数统计的相干斑强度估计

针对Lee J.S.等［3］算法的不足，本文提出了一种基于方差系数统计的相干斑强度估计算法，具体的思路是:

先将整个SAR图像划分为一个个互不重叠的正方形小区域(假设尺寸为W×W)，再计算每个区域的均值和标准差并绘制均值平方—方差平面图，最后使用一个估计方法获得结果，其核心步骤是如何估计通过均值平方—方差平面中点数最多的直线的斜率，换种角度考虑就是出现频率最多的方差系数。这个估计过程可从统计学角度求解，估计所有的方差系数的概率密度函数(Probability Density Function-PDF)，在PDF最大值出现的地方所对应的方差系数值就是所要求的最优估计:

其中，f(γY)代表γY的概率密度函数。

直方图是一种应用最为广泛，并且简单、有效的PDF估计方法［6］。假设x0为起始点，h为条形小区间的宽度，那么在这些小区间的直方图可以定义在一系列区间［x0+mh，x0+(m+1)h］上，对于x点处的PDF可以估计为:

式中 m=0，1，．．．，M-1，其中，Nm表示区间［x0+mh，x0+(m+1)h］内的样本个数，并假设条形小区间的总数为M，样本总数为n。

在方差系数的概率密度函数f(γY)的估计中，起始点γY0等于0(当小区域的方差为0时)，那么区间就可以简化为，那么此时的估计可以表示为:

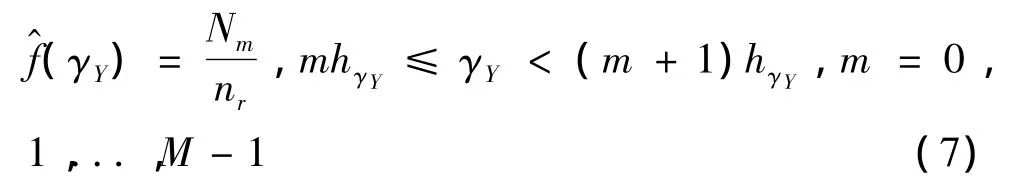
其中，nr表示整幅SAR图像划分的小区域的个数。

本文所提出算法的具体执行步骤是:

a.将一幅给定的SAR图像划分为数个互不重叠的W×W的图像块;

b.根据公式(2)计算划分得到的所有图像块的方差系数γY;

c.根据公式(7)利用直方图法计算这些方差系数的概率密度函数;

3 实验结果与分析

为了测试本文所提算法的性能，我们首先选择了两幅自然图像:Cameraman(256×256，图2(a))和Peppers(256×256，图2(b))并分别加不同视数的幅度模拟相干斑。Peppers和Cameraman分别代表了包含较多同质场景与异质(Heterogeneous)的两类图像。在实验中，所有图像被划分为4×4(W=4)的小块，在方差系数的PDF的估计中，取条形小区域的宽度h=0．001。表1给出了在不同等级的模拟相干斑下，使用本文所提算法对相干斑强度的估计结果。可以看出，对不同等级和不同场景的图像，所提算法都可以获得很高的估计精度。对于异质区域较多的Cameraman，其平均偏差为5.17%，相比较而言，同质区域较多的Peppers，其平均估计偏差则只有2.03%，并且最低的偏差只有0.46%。此外，也可以发现随着相干斑强度的降低，本文所提算法的估计精度逐渐提高;所提算法对同质区域较多的Peppers在大多数情况下的估计精度要高于异质区域较多的Cameraman。

图2 不同等级和不同场景的模拟相干斑比较图

一幅真实的单视幅度SAR图像Howland Forest(401×386，图2(c))被用来测试本文所提算法，以及对比所提算法与Lee J.S.等在文献［3］中提出的扇形区间估计算法的性能。本文所提算法的对相干斑方差的估计为0.509，而Lee J.S.在文献［3］中的估计结果为0.508，其理论值为0.5227。对于真实图像而言，我们的估计结果与扇形区间估计法的结果非常接近。但是相比较而言，Lee J.S.的方法需要额外选择扇形区间角度Δθ以及扇形区间重叠角度Od。由于一个小的Δθ可能会导致错误的结果，而一个大的Δθ则会使估计精度降低，因此Δθ的选择需要更多的人工经验，而本文所提算法则是自动的不要人工选择参数，实现了真正意义上的无监督估计。

表1 本文所提算法在不同等级的模拟相干斑下的估计结果

4 结束语

本文提出一种基于方差系数统计无监督的SAR相干斑强度估计算法，首先将整幅SAR图像划分为一个个互不重叠的小区域，接着计算每个小区域的方差系数。根据最优的相干斑方差系数估计就是出现频率最多的那个方差系数值这一基本思想，利用直方图估计方差系数的概率密度函数以及区间扫描的方法求得概率密度函数的最大值和相应的最优相干斑方差估计值。相比于传统估计方法，本文算法自动执行、执行过程简单并且算法复杂度低，很适合工程应用。

［1］Oliver C.，Quegan S.Understanding synthetic aperture radar images［M］.Boston，MA:Artech House，1998.

［2］Henri Maitre［法］编，孙洪等译.合成孔径雷达图像处理［M］.北京:电子工业出版社，2005.

［3］Lee J.S.，Hoppel K.，and Mango S.A.Unsupervised estimation of speckle noise in radar images［J］.International Journal of Imaging Systems and Technology，1992，4:298-305.

［4］Lee J.S.，Hoppel K.Noise modeling and estimation of remotely-sensed images［C］.In Proc.IGARSS，1989，2:1005-1008.

［5］Sathit I.Speckle noise estimation with generalized Gamma distribution［C］.In Proceedings SICE-ICASE International Joint Conference，2006:1164-1167.

［6］Knuth D.The art of computer programming，volume 3:sorting and searching［M］.third ed.New Jersey:Addison-Wesley Publishing Company，1997:106-110.