海-陆混合路径对雷电电磁场传播的影响

李 涵 邓雨荣 朱时阳 杨 璟

（1.广西电网公司电力科学研究院 南宁 530023 2.武汉大学博士后流动站 武汉 430072 3.南京信息工程大学大气物理学院 南京 210044）

1 引言

云-地闪电（简称地闪）回击过程产生强烈的微秒和亚微秒量级高频电磁辐射场，通过耦合效应对电子产品以及输变电设备等造成危害[1-3]。由于高频脉冲信号沿有限电导率地表传播时产生快速衰减[4-6]，因此，对雷电电磁波谱的测量通常借助于海面。因海水电导率为4S/m，远远大于土壤的电导率（0.1～0.000 1 S/m），所以其对电磁场的影响远小于陆地。Weidman等[7,8]对海洋雷暴产生的电磁波谱进行了观测研究，发现其峰值介于 1～10kHz的VLF频段，在10kHz到1MHz之间，振幅谱随频率而线性减小。在1MHz以上，以频率平方的倒数衰减，超过10MHz以上接近频率三次方的倒数急剧衰减。Willett等[9]认为地闪回击电磁波谱分布范围的上限是20MHz。Ming和Cooray[10]等曾利用简单的Newmann-Pierson经验模型研究了海浪起伏对地闪回击电磁场传播的影响，发现15m/s的海风引起的海浪起伏可能造成 10MHz以上雷电电磁波的快速衰减。不过，他们假定传播路径全部为海面，没有讨论陆地部分对电磁场传播的影响。实际测量雷暴电磁波谱是将仪器架设在沿海地区，所以雷电电磁场的传播路径是电导率呈垂直分层的海-陆混合路径，海水与陆地的边界效应可能会对电磁场造成一定的影响。因为与海浪起伏不平的海面相比，陆地部分的电导率相对较小且地形地貌的起伏更加复杂，粗糙陆地部分对雷电电磁场传播的影响与海面明显不同。因此，研究海-路混合路径对雷电电波传播的影响是很有必要的。

目前，国内外研究者在研究雷电电磁波沿地表传播时，通常假定地表光滑[11-16]，这种处理方式在近距离不会产生偏差，但当观测研究距闪电通道几十公里范围的雷电电磁传播时，复杂地形地貌的影响有必要考虑。至于地形地貌的模拟，目前通常采用分形方法。从大范围看，不同地域的地形地貌具有分形自相似的一些特征，通常称为分形地貌学。起伏不平的自然地表既不是完全随机的、也不是完全周期重复的。分形方法的引入为复杂地表的模拟提供了一种新的手段[17]。因此，本文将利用分形方法模拟粗糙海-陆混合路径，研究其对地闪回击电磁场传播的影响。这对沿海地区雷电定位以及雷电电磁场测量等许多方面都具有重要的学术和应用价值。

2 任意粗糙地表雷电电磁场计算方法

当雷电地闪回击过程产生的电磁场沿任意粗糙地表传播时，距离闪电通道为d的地表面任一点处的垂直电场为[18]

式中，Ev,σ(0,d,jω)与 Ev,∞(0,d,jω)与分别为有耗地表和理想地表面的垂直电场；W(0,d,jω)是混合传播路径的频域衰减因子。从式（1）看出，计算任意粗糙地表附近的雷电电磁场，关键是计算衰减因子W(0,d,jω)。如图1所示，假定雷电发生在海面，电磁场沿粗糙海-陆混合路径传播时的衰减因子为[19-22]

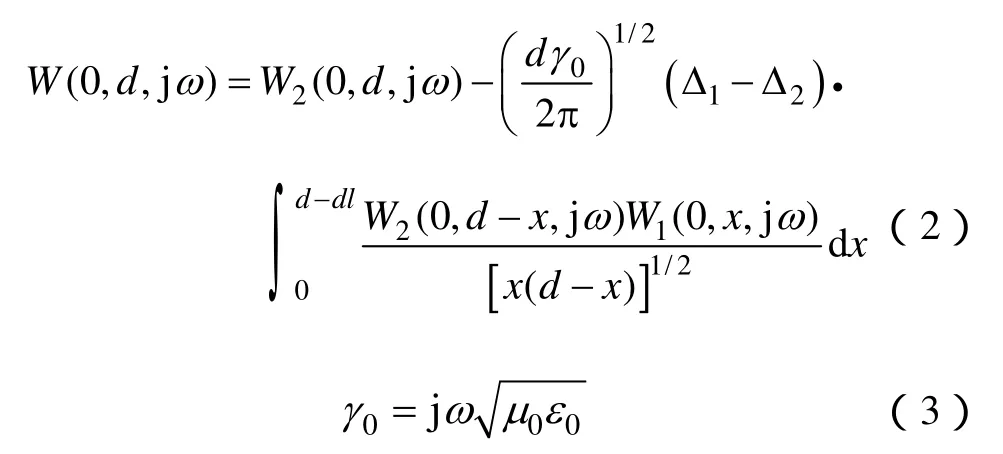
式中，W1(0,d,jω)和 W2(0,d,jω)分别为海面和陆地部分的衰减函数，满足

式中，n=1，2分别表示海面和陆地；d为观测距离（dl为陆地部分的长度）；ω为角频率；c为光速；。Δn为归一化的表面阻抗和等效表面阻抗，其等效形式可表示为[23,24]

图1 粗糙海-陆混合传播路径电导率垂直分布示意图和模拟示意图Fig.1 Propagation of the lightning electromagnetic fields along a rough and mixed path

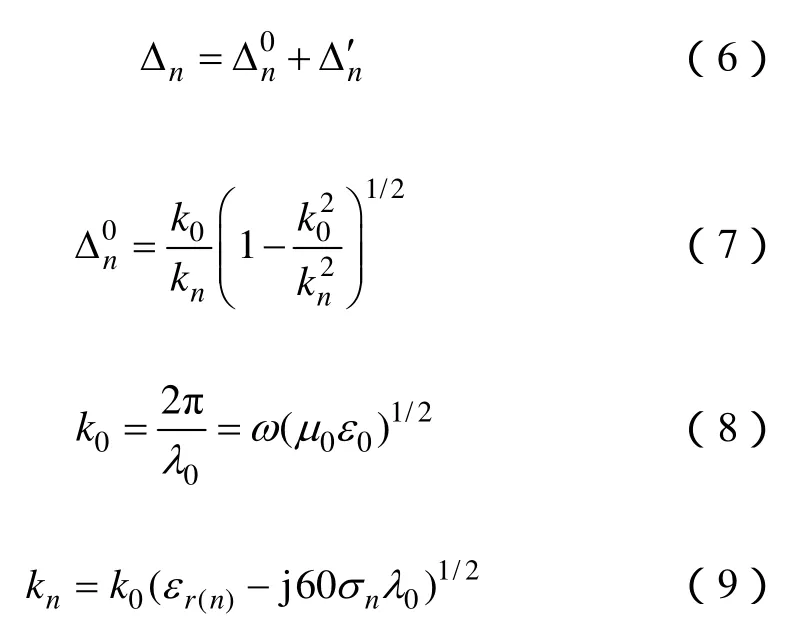
当 n=1，V1(γ,η)表示粗糙海面部分的高度谱密度；当n=2，V2(γ,η)表示粗糙陆地部分的高度谱密度。因此，如果知道粗糙海面和陆地的高度谱密度函数（V1(γ,η)和 V2(γ,η)），结合式（2）～式（12），就可以计算海-陆混合路径的衰减函数。下面介绍粗糙海面和陆地的高度谱密度函数Vn(γ,η)。

3 分形粗糙海-陆混合传播路径模型建立

自然界中的许多粗糙表面，如海表面、植被、森林和山地覆盖的陆地等具有非线性的几何结构，且都在一定的尺度范围内存在统计意义上的自相似性，这些性质促使众多学者将分形理论应用在粗糙面的电磁散射等研究中[25-28]。对于海面来说，海浪的高度一般能达到数英尺，并且在大的波浪上面还覆盖着小的风浪和毛细波，即由大尺度的重力波和小尺度的张力波组成，因此特别适合用分形描述[29]。本文采用Pierson-Moscowit（PM）海谱模型来模拟粗糙海面[30]。PM 谱代表充分成长的风浪谱，其在海浪研究及有关的工程问题中被广泛应用，其表达式为

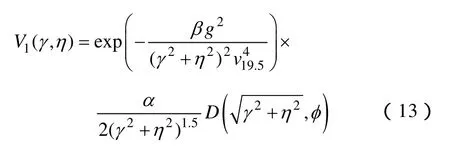
式中，α=8.1×10-3；β=0.74；g是重力加速度；v19.5表示海面上方19.5m处的风速，v19.5=15 m/s；φ表示风向与x轴方向的夹角；γ和η分别为沿x轴、y轴的径向波数；k0为基波波浪的空间波数；是与海风传播方向有关的方向分布函数。最适合中国海域的 Donelan方向函数模型为[22]

至于粗糙陆地，其地形起伏与海面不同，通常采用分形布朗运动方法Fractional Brownian Motion来模拟，其高度谱密度为Falconer[30]给出

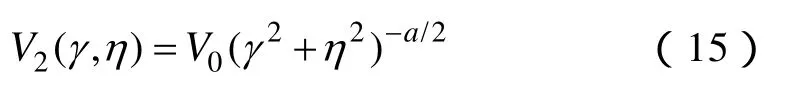
式中，V0=h2/2πL，a=8-2D；D是分形维数；L是相关长度；h是粗糙高度方均根。值得注意的是，由于海浪的起伏是随着风速的大小和方向而变化的，但陆地粗糙面的起伏是固定的，因此，为了模拟粗糙陆地，通常采取与海浪不同的仿真方法，本文采用分形方法来模拟粗糙陆地。当然随着分形维数、相关长度和粗糙高度方均根的改变，相应的粗糙陆地表面对雷电电磁场的影响是不同的。

4 模拟结果分析

假定地闪回击通道笔直且垂直于地面，回击电流从通道底部始发，沿通道以速度v = 1.9×108m/s向上传播。电流波形随高度的衰减满足MTLL回击模型，假设回击通道为8km。回击电流包含击穿电流和电晕电流两部分，击穿电流和电晕电流都采用Heidler[31]指数表达式计算，其表达式如下：

式中，i0是电流幅值；τ1是电流上升时间常数；τ2为电流衰减时间常数。

表1为继后回击电流对应的参数[32]。

表1 继后回击电流参数Tab.1 Parameters for the subsequent return stroke currents

图2给出了粗糙海-陆混合传播路径对雷电电磁场传播的影响。曲线1～4具体参数见表2，点画线为光滑均匀海面传播（不考虑陆地）。选取的回击电磁场频率范围为几赫兹至30MHz，计算的频率幅值采用 dB表示方法（对幅值取自然对数后再乘以20），电场单位为V/m。海面电导率和电容率分别为：σ1=4S/m，εr1=80；陆地电导率和电容率分别为：σ2=0.01 S/m，εr2=10。比较图2中时域电磁场曲线（点画线和实线 1～4）可知，粗糙海-陆混合路径对垂直电场幅值几乎没有影响，但对上升沿时间的影响较大。因为随着地表粗糙度的增大，电磁场高频分量快速衰减。比较频域电磁场曲线，可以看出，海陆混合路径对电磁场的衰减远大于海面，频率超过2 MHz的电磁场受陆地部分的衰减更明显。如图2d，海面传播99km、陆地传播1km，陆地部分仅占1%，但海-陆混合路径对电磁场高频分量的衰减远大于均一海面。总体上，曲线1～4反映出，随着地表粗糙度的增加，高频衰减有增大的趋势。

图2 粗糙海-陆混合路径对地闪继后回击电磁场传播的影响Fig.2 Lightning-radiated vertical electric fields along a rough and ocean-land mixed path

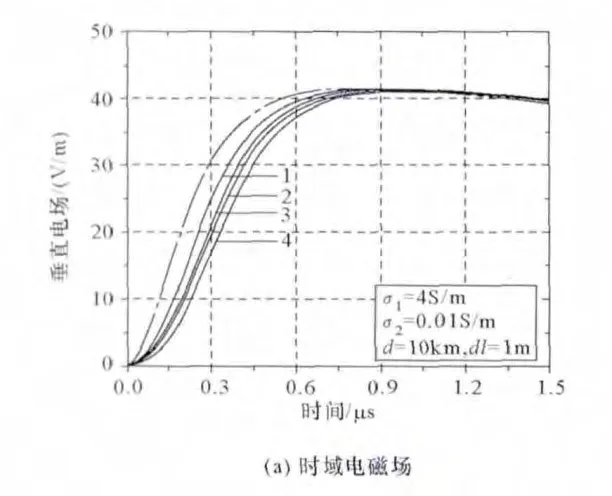
表2 海-陆混合路径的粗糙度Tab.2 The root-mean-square heights(RMSH) for the rough ocean-land mixed path

图3给出了混合路径中陆地部分长度（图1中的dl）对电磁场传播的影响。图中海面传播路径固定为50km(d-dl=50km)，陆地传播路径dl分别设定为0、1m、10m、20m、50m 和100m（dl=0m表示传播路径全部为海面）。由图可见，即使陆地部分仅为几十米，对雷电电磁波2MHz以上高频段的衰减也不容忽视。

图3 混合路径中陆地部分长度（dl）对电磁场传播影响Fig.3 The land section width(dl) on the lightning electromagnetic fields propagating along an ocean-land mixed path

图4进一步给出了雷电电磁场从海面到陆地（图4a）或从陆地到海面（图4b）传播时，在边界面附近产生的突变。可以看出，当雷电发生在海面，电磁场从海面向陆地传播时，在边界面附近，垂直电场突然减小。这是由于陆地的电导率远远小于海水，电磁波高频分量迅速衰减造成的。不过，当雷电发生在陆地、向海面传播时，在海陆交界面附近电场有一个相对增大的区域，范围可达几百公里。随着两层介质电导率差异越大以及电磁波频率越高，两种介质的边界效应越明显。

图4 电磁场在海-陆混合路径边界的突变Fig.4 Electromagnetic field decrease rapidly near the interface propagating from the ocean to the land section

另外，从式（16），在分形粗糙海面 PM 谱Donelan方向函数模型中，φ是风向与x轴方向的夹角。如果假定雷电电磁场沿 x轴传播，则φ就是电磁场传播方向与海风方向（即海浪起伏的方向）的夹角。从图5a看出，如果电磁场传播路径全部为海面，则电磁场衰减与其传播方向有关。当电磁场传播方向与海风一致时衰减最大（φ=0°），与海风方向垂直时最小（φ=9 0°）。不过，如果电磁场穿过海-陆混合区域进入陆地，则由于陆地部分对高频电磁场的衰减远远大于海浪，因此，海浪的影响可忽略不计。

图5 传播方向对电磁场衰减的影响Fig.5 Effect of the different propagation direction on the lightning electromagnetic fields

5 结论

本文利用Barrick等效表面阻抗法和Wait近似算法等研究了粗糙海-陆混合路径对雷电电磁场传播的影响。发现当雷电发生在海面，电磁场沿海-陆混合路径传播时，长度仅为几十米的陆地部分已经对2MHz以上电磁场产生不容忽视的影响。当关注的频段超过10MHz时，还需要考虑浪高的影响。因此，Weidman等人[7,8]在海边附近测量的雷电电磁波谱还需要考虑电磁波沿海-陆混合路径传播的边界效应，如他们发现超过1MHz以上频段的电磁场快速衰减现象应该计及海-陆混合路径的传播衰减效应，而不纯粹是雷电磁场自身的特征。

[1] Rubinstein M.An approximate formula for the calculation of the horizontal electric field from lightning at close,intermediate,and long range[J].IEEE Transactions on Electromagnetic Compatibility,1996,38(3): 531-535.

[2] Cooray V.Some considerations on the Cooray-Rubinstein formulation used in deriving the horizontal electric field of lightning return strokes over finitely conducting ground[J].IEEE Transactions on Electromagnetic Compatibility,2002,44(4):560-566.

[3] Master M J,Uman M A.Lightning induced voltages on power lines: Theory[J].IEEE Transactions on Power Apparatus and Systems,1984(9): 2502-2518.

[4] Delfino F,Procopio R,Rossi M.Lightning return stroke current radiation in presence of a conducting ground: 1.Theory and numerical evaluation of the electromagnetic fields[J].Journal of Geophysical Research,2008,113(D5): D5110.

[5] Cooray V,Fernando M,Sörensen T,et al.Propagation of lightning generated transient electromagnetic fields over finitely conducting ground[J].Journal of Atmospheric and Solar-Terrestrial Physics,2000,62(7): 583-600.

[6] Cooray V.On the accuracy of several approximate theories used in quantifying the propagation effects on lightning generated electromagnetic fields[J].IEEE Transactions on Antennas and Propagation,2008,56(7): 1960-1967.

[7] Weidman C D,Krider E P.Submicrosecond risetimes in lightning return-stroke fields[J].Geophysical Research Letters.1980,7(11): 955-958.

[8] Weidman C D,Krider E P,Uman M A.Lightning amplitude spectra in the interval from 100kHz to 20 MHz[J].Geophysical Research Letters,1981,8(8):931-934.

[9] Willett J C,Bailey J C,Leteinturier C,et al.Lightning electromagnetic radiation field spectra in the interval from 0.2 to 20 MHz[J].Journal of Geophysical Research,1990,95(D12): 20367-20387.

[10] Ming Y,Cooray V.Propagation effects caused by a rough ocean surface on the electromagnetic fields generated by lightning return strokes[J].Radio Science,1994,29(1): 73-85.

[11] Qie X,Jiang R,Wang C,et al.Simultaneously measured current,luminosity,and electric field pulses in a rocket-triggered lightning flash[J].Journal of Geophysical Research,2011,116(D10102):1-11.

[12] Zhang Q,Qie X,Wang Z,et al.Simultaneous observation on electric field changes at 60m and 550m from altitudetriggered lightning flashes[J].Radio Science,2009,44(RS1011): 1-5.

[13] Zhang Q,Liu X,Yang J,et al.The characteristics and simulation of close leader/return stroke field change waveforms[J].Radio Science,2011,46(RS1017): 1-8.

[14] Zhang Q,Yang J,Wang Z.Measurements and simulation of the mcomponent current and simultaneous electromagnetic fields at 60 m and 550 m[J].Atmospheric Researchm,2011,99: 537-545.

[15] Shoory A,Moini R,Rachidi F.Validity of simplified approaches for the evaluation of lightning vertical electric field above a horizontally stratified ground[J].IEEE Transactions on Electromagn.Compat,2010,52(3),657-663.

[16] Cooray V.Propagation on effects due to finitely conducting ground on lightning-generated magnetic fields evaluated using Sommerfeld's integrals[J].IEEE Transactions on Electromagnetic Compatibility,2009,51(3): 526-531.

[17] Mandelbrot B B.The fractal geometry of nature[M].New York: Freeman,1982.

[18] Shoory A,Moini R,Sadeghi S H H,et al.Analysis of lightning-radiated electromagnetic fields in the vicinity of lossy ground[J].IEEE Transactions on Electromagnetic Compatibility,2005,47(1): 131-145.

[19] Wait J R.Recent analytical investigations of electromagnetic ground wave propagation over inhomogeneous earth models[J].Proceedings of the IEEE,1974,62(8): 1061-1072.

[20] Wait J R.The ancient and modern history of EM ground-wave propagation[J].IEEE Antennas and Propagation Magazine,1998,40(5): 7-24.

[21] Wait J,Walters L.Correction to curves for ground wave propagation over mixed land and sea paths[J].IEEE Transactions on Antennas and Propagation,1963,11(3): 329.

[22] Wait J,Walters L.Curves for ground wave propagation over mixed land and sea paths[J].IEEE Transactions on Antennas and Propagation,1963,11(1): 38-45.

[23] Barrick D E.Theory of HF and VHF propagation across the rough sea,2,Application to HF and VHF propagation above the sea[J].Radio Science,1971,6(5): 527-533.

[24] Berizzi F,DalleMese E.Scattering from a 2D sea fractal surface: fractal analysis of the scattered signal[J].IEEE Transactions on Antennas and Propagation,2002: 912-925.

[25] Jakeman E.Scattering by a corrugated random surface with fractal slope[J].Journal of Physics A:Mathematical and General,1982,15: L55.

[26] 郭立新,吴振森,柯熙政.二维带限分形粗糙面电磁散射的基尔霍夫近似[J].电子学报,2000,28(9):128-130.Guo Lixin,Wu Zhensen,Ke Xizheng.Electromagnetic scattering from 2D band-limited fractal surface using kirchhoff approximation[J].Acta Electronica Sinica,2000,28(9): 128-130.

[27] 郭立新,徐燕,吴振森.分形粗糙海面高斯波束散射特性模拟[J].电子学报,2005,33(3): 534-537.Guo Lixin,Xu Yan,Wu Zhensen.Modeling of the scattering from fractal rough sea surface with Gaussian-Beam incidence[J].Acta Electronica Sinica,2005,33(3): 534-537.

[28] 王运华.海面及其与上方简单目标的复合电磁散射研究[D].西安: 西安电子科技大学,2006.

[29] Franceschetti G,Iodice A,Migliaccio M,et al.Scattering from natural rough surfaces modeled by fractional Brownian motion two-dimensional processes[J].IEEE Transactions on Antennas and Propagation,1999,47(9): 1405-1415.

[30] Falconer K J.Fractal geometry: mathematical foundations and applications[M].New Jersey: John Wiley & Sons Inc,2003.

[31] Heidler F.Traveling current source model for LEMP calculation[C].Proceedings of the 6th International Symposium on Electromagnetic Comatibility,Zurich,Switzertand,1985: 157-162.

[32] Rachidi F,Janischewskyj W,Hussein A M,et al.Current and electromagnetic field associated with lightning-return strokes to tall towers[J].IEEE Transactions on Electromagnetic Compatibility,2001,43(3): 356-367.