开发模型与水驱曲线联解预测方法
2014-06-17王胤渊陈小凡刘峰杨博义
王胤渊,陈小凡,刘峰,杨博义
(西南石油大学油气藏地质及开发工程国家重点实验室,四川 成都610500)
0 引言
水驱曲线是水驱开发油田固有的特征曲线,不仅可预测油田的可采储量和采收率,还可对油田可动储量作出评估,因而在我国得到了广泛应用[1-9]。然而,油田开发指标与开发时间密切相关,水驱曲线却无法预测油藏开发指标与开发时间的关系。开发模型法也是一种重要的油藏工程预测方法,该方法以数理统计为基础,通过开发历史拟合确定油气藏的数学模型,并对未来的生产指标进行预测。其中,威布尔(Weibull)预测模型不仅可预测油气田产量、累计产量随时间的变化规律,还可预测可采储量、最高年产量及发生时间,但无法预测含水率等开发指标[10-11]。
在目前已有的20 多种水驱曲线中,甲型水驱曲线的应用范围最广,精确度最高,本文将其与Weibull 模型相结合,建立了一种新的预测模型,用以预测含水率随时间的变化规律[12-17]。
1 模型推导
1.1 Weibull 预测模型
Weibull 预测模型是基于数理统计学中的Weibull分布,经推导转换得出的,其基本关系式包括:
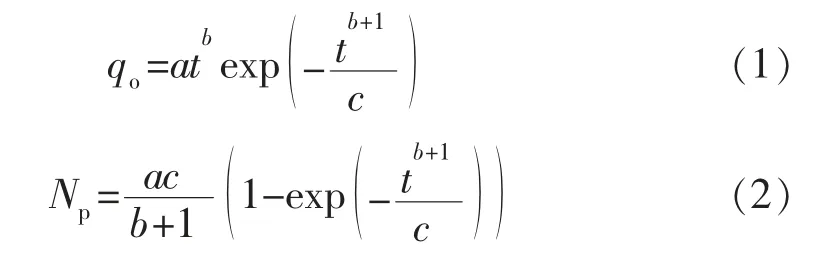

式中:qo为年产油量,104t;t 为油田开发时间,a;Np为累计产油量,104t;NR为可采储量,104t;a,b,c 为模型的经验常数。
将式(1)两边对时间t 求导,并令dqo/dt=0,得到最高年产量发生时间tm:
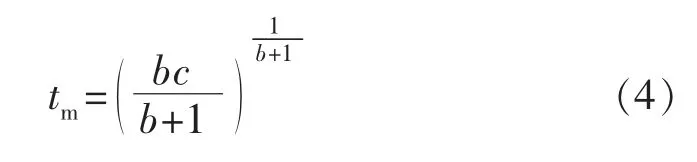
将式(4)代入式(1),得到最高年产量qm:
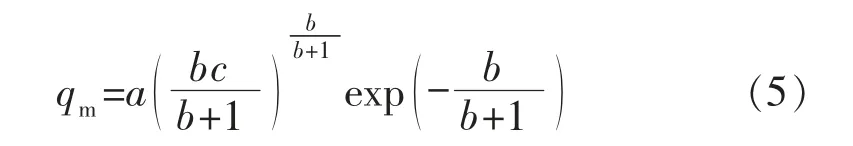
联立式(2)与式(5),得到最高年产量对应的累计产油量Npm:
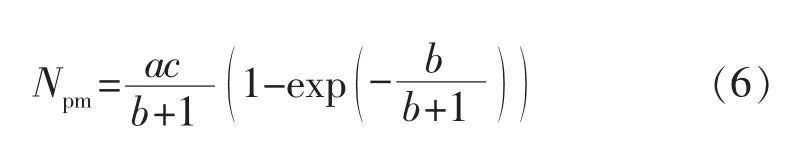
1.2 甲型水驱曲线
甲型水驱曲线最早是由马克西莫夫提出的,1978年童宪章将其命名为甲型水驱曲线,其基本关系式为

式中:Wp为累计产水量,104t;A,B 为经验常数。将式(7)两边对时间t 求导,可得:
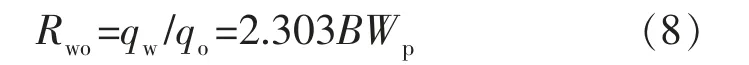
式中:Rwo为生产水油比;qw为年产水量,104t。
结合Rwo与含水率fw的关系式,进一步推导得出:
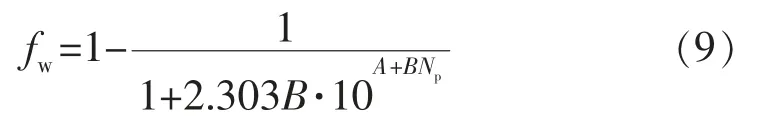
1.3 模型联解
将式(2)代入式(9),即可得到不同开发时间的含水率预测公式:
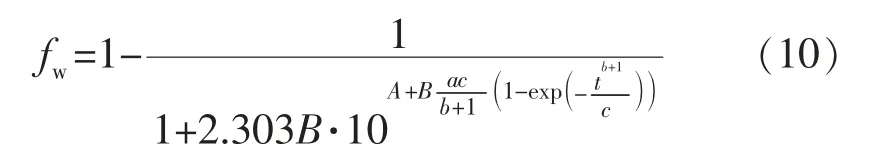
为了确定模型常数a,b,c,将式(1)两边取自然对数,并令,则

可采用单变量寻优算法对式(11)进行求解,即假设一系列b 值,并绘制相应的关系曲线,对曲线进行线性回归,最佳拟合直线对应的b 值即为常数b。再根据拟合直线的截距α 和斜率β,由确定参数a,c。为确保模型常数a,b,c 的值正确可靠,可先利用式(1)、(2)、(10)计算理论产油量、累计产油量和含水率,而后将其分别与实际值进行对比。只有当各生产指标达到最佳拟合效果时,参数a,b,c 才具有使用价值。将可用的模型参数a,b,c 代入式(10),即可进行含水率随开发时间变化规律的预测。
2 实例应用
借用文献[14]中大庆南二三开发区葡一组油田的开发数据,利用Weibull 预测模型与甲型水驱曲线的联解法进行含水率等生产指标的预测,并与实际结果进行对比,以验证联解模型的可靠性与实用性。
根据式(7),在半对数坐标系中绘制葡一组油田的Wp-Np关系曲线(见图1)。可以看出,lg Wp-Np呈较好的线性关系,对直线段进行线性回归,相关系数高达0.999 4。由此可见,甲型水驱曲线能较好地反映该油田的水驱开发特征。
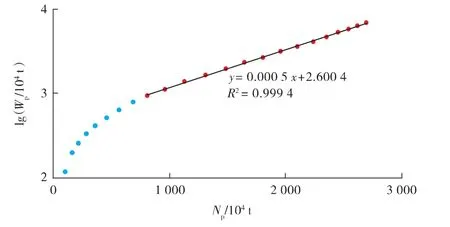
图1 葡一组油田lg Wp-Np 关系
假设系列b 值(从1 开始试取),依据式(11)绘制不同b 值条件下的关系曲线(见图2)。对曲线进行线性回归,可以看出,当b=1.125 时曲线的相关系数最大,此时直线的截距α 为2.927 3,斜率β 为0.002 8,相关系数为0.997 6。由a-α 及c-β 关系式,求得a=18.632 4,c=357.142 9。
将a,b,c 的值分别代入式(4)—(6),得到最高年产油量为176.05×104t,对应的开发时间和累计产油量分别为11.79 a 和1 287.2×104t,与实际年产油量及累计产油量随时间变化曲线的最高点基本吻合(见图3)。
同时,将a,b,c 的值分别代入式(1)、式(2)和式(10),可以得到葡一组油田产油量、累计产油量和含水率的理论预测值。将预测数据与实际生产数据进行对比(见图3),可以看出,联解模型的预测结果总体上与各开发指标随开发时间的变化趋势相吻合。其中,在产量上升阶段,年产油量的预测值与实际值的误差相对较大,但是在产量递减阶段,预测精度较高,误差较小。分析认为,这主要是由于水驱曲线一般用于含水率大于50%的油田开发阶段。由此可见,确定的a,b,c 值是比较可靠的。为此,应用联解模型对葡一组油田未来20 a 的开发生产指标进行了预测(见图3)。
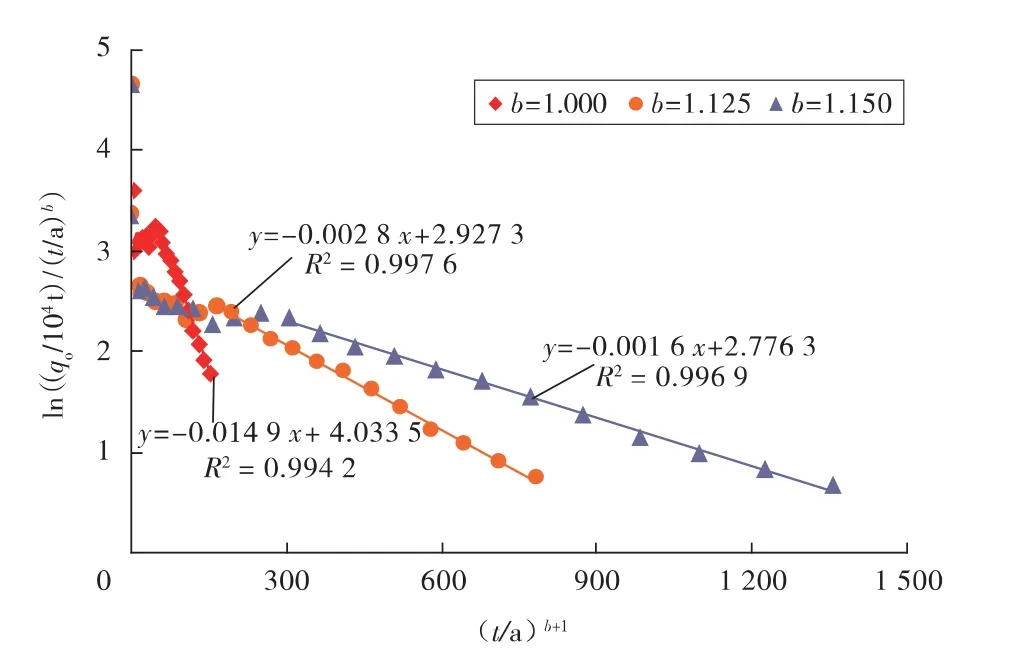
图2 不同b 值下的ln (qo /tb)-tb+1 关系曲线
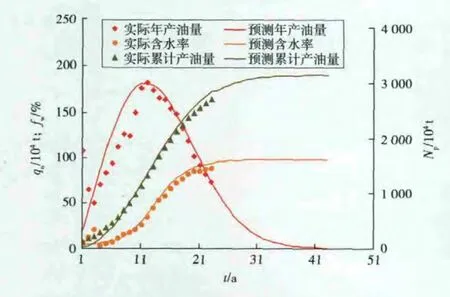
图3 葡一组油田生产指标预测值与实际值对比
3 结束语
将Weibull 预测模型与甲型水驱曲线相结合,推导得出开发指标随开发时间变化规律的联解预测模型,克服了2 种单一方法的局限性,实现了含水率随开发时间变化规律的预测。从应用结果看,预测结果与实际生产数据基本吻合,但仍存在一定误差,有待进一步研究与改进。
[1]李传亮.油藏工程原理[M].北京:石油工业出版社,2005:211-278.
[2]吴宏利,孔自超,李蕾,等.一种研究含水率上升规律的新方法[J].断块油气田,2001,8(3):37-38.
[3]张虎俊.预测油田产量的新模型及其应用[J].大庆石油地质与开发,1995,14(4):40-45.
[4]俞启泰.两种水驱特征曲线及其应用[J].大庆石油地质与开发,1997,16(1):31-34.
[5]曹立迎.底水油藏水平井水淹规律经验模型[J].断块油气田,2012,19(3):323-326.
[6]王怒涛.新型水驱特征曲线系列[J].西南石油大学学报:自然科学版,2007,29(2):103-105.
[7]王华,邴绍献,张海燕,等.特高含水期水驱油效率计算新方法[J].断块油气田,2013,20(2):201-203.
[8]陈元千.水驱曲线关系式的推导[J].石油学报,1985,6(2):69-78.
[9]阎静华,许寻,杜永波.计算相渗曲线的新方法:甲型水驱曲线法[J].断块油气田,2001,8(1):38-40.
[10]俞启泰.Weibull增长曲线预测油田开发指标的0.632 12准数[J].石油勘探与开发,1998,25(2):69-78.
[11]Wang Jixia,Miao Yu.Bivariate generalized Weibull distribution model [J].Journal of Mathematics,2012,32(4):69-73.
[12]孙来喜,付国民,冯文光,等.基于Logistic模型及水驱曲线的一种综合预测模型[J].矿物岩石,2002,22(4):97-100.
[13]赵锋,陈祥光.Γ模型与水驱曲线的一种联解法[J].特种油气藏,2004,11(1):44-46.
[14]陈元千,赵庆飞.Weibull预测模型与乙型水驱曲线的联解法[J].新疆石油地质,2000,21(5):405-407.
[15]魏洪涛,王怒涛.两种新型水驱特征曲线系列[J].西南石油大学学报:自然科学版,2009,22(6):343-347.
[16]张光强,朱有志,刘忠云.一种简易的水驱特征曲线的校正方法[J].断块油气田,1997,4(3):30-32.
[17]罗洪,俞启泰.用增长曲线一体化法预测水驱油田开发指标[J].断块油气田,2001,8(3):19-24.
