基于蚁群算法的丛式井井口分配方法研究

闫铁，焦文夫，毕雪亮，徐婷，于洋,逯广东

（1.东北石油大学提高油气采收率教育部重点实验室，黑龙江 大庆163318；2.中国石化华北油田分公司工程监督中心，河南 郑州450006；3.中国石油吉林油田公司钻井工艺研究院，吉林 松原138000）

丛式井具有投资小，见效快，便于集中管理等优点，是提高油田采收率和采油速度的经济有效手段［1-3］，在开发常规或非常规油气资源中应用日益增多。丛式井井口间距较小，优化井口分配，可有效减少碰撞概率及施工难度。国内外学者多以“水平位移之和最小”、“总井深之和最小”、“总井深与总水平位移之和最小”等为井口分配基本原则［4-8］，但相应的数学模型及求解方法研究却很少。笔者以水平位移之和最小且井口连接靶点的线段在水平面上的投影不相交或尽量少相交为分配方案模型，以带有惩罚机制的蚁群算法［9-11］为求解方法，为设计人员提供较为科学的计算方法和手段。

1 丛式井井口分配模型求解

1.1 分配模型

钻井设计时，要对井口与靶点进行分配。先确定井口与靶点的对应关系，再进行井眼轨迹设计，所以，选择合理的靶点对应井口，对于丛式井钻井是非常必要的。实践证明，井口与靶点的水平位移增大，不仅会增大施工难度且会增加钻井成本，井口连接靶点的线段在水平投影面上相交会增大钻井碰撞事故概率。所以在分配时应遵循井口与靶点连线在水平投影面上不相交或少相交，而且使水平位移之和最小的原则。

井口分配时有3 种投影情况： 井口—靶点水平投影平行；井口—靶点水平投影相交；井口—靶点水平投影延长线相交。已知水平投影坐标井口A（X1，Y1），B（X2，Y2），靶点C（X3，Y3），D（X4，Y4），如图1所示。易得井口—靶点水平投影平行模型，若，需判断投影相交还是投影延长线相交，如图2所示。

假设交点为（X0，Y0），则

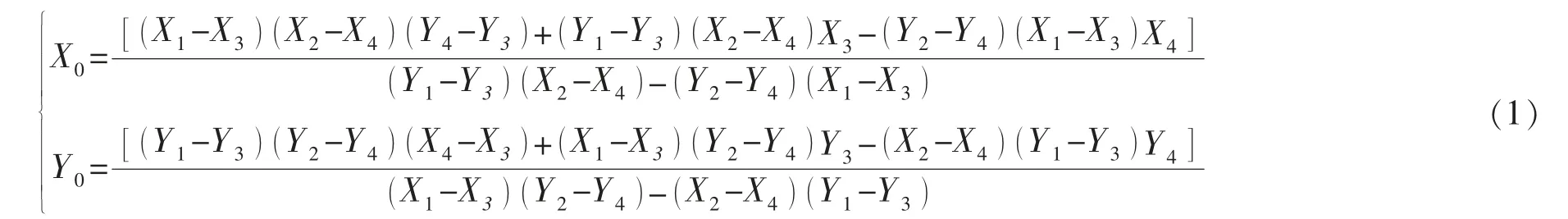
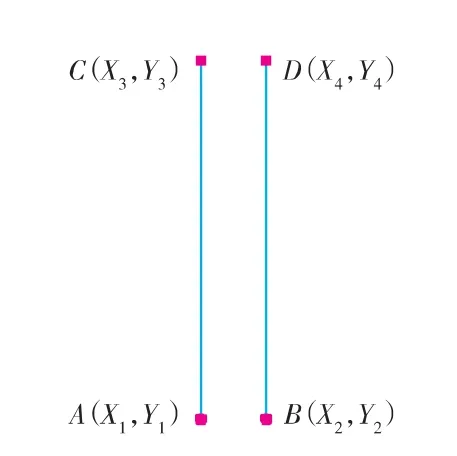
图1 水平投影平行

图2 水平投影相交或延长线相交

判断水平投影交点的约束条件为

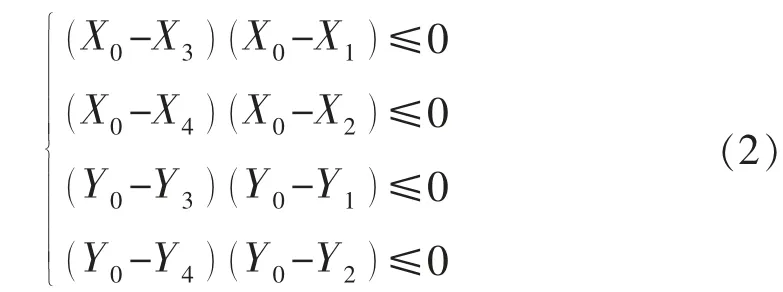
只有同时满足式（2）中所有约束条件，点（X0，Y0）才是井口A—靶点C 与井口B—靶点D 在水平投影面上的交点，否则是延长线上的交点。由于水平投影相交会增加施工难度及碰撞概率，所以将不相交的方案作为主选方案，而将有交点的方案作为次选方案，利用下文中的惩罚机制控制次选方案的重要性。以井口到靶点在水平投影平面连线和最小为优化指标，建立井口分配模型：

式中：N 为与井口匹配靶点的组合数；（xit，yit） 为井口坐标，（xi，yi）为靶点坐标。

1.2 引入惩罚函数的蚁群求解方法

1.2.1 路网铺设

利用蚁群算法解决井口分配问题，首先将其转换成搜索路径最短的组合优化［12］问题。

以第1 井口为蚁穴位置，将井口距其靶点水平投影位移作为节点间路径，其他井口作为交叉点，最后1口井对应的靶点即为食物地点。即把井口分配问题转换成路径最短问题，组合最短路径上的各井口—靶点，就是所求的最优分配方案。以基本的3 组井口—靶点为例（见图3），包括井口1，2，3 和靶点A，B，C。

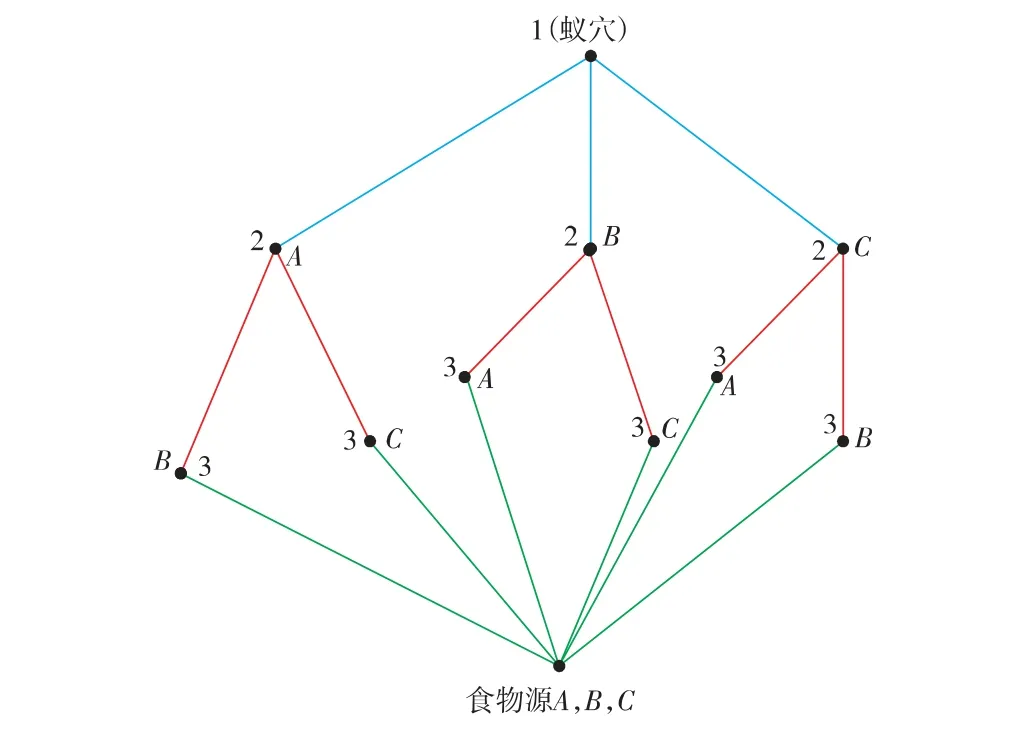
图3 井口—靶点分配组合

1.2.2 蚁群求解算法

蚁群间的相互协作是蚂蚁能够用最短的路径找到食物源或蚁穴的最主要原因，通过嗅出路径上的信息素，指导自己对路径的选择；同时，信息素随时间推移而逐渐挥发，路径短的所需时间短，信息素挥发少，反过来对后续蚂蚁起到指导作用，随着蚂蚁对路径的不断选择，越来越多的蚂蚁找到最短路径，形成蚁群的正反馈现象。

蚂蚁k 在井口i 选择靶点j 为目标的概率是节点启发信息ηij与到目标靶点的信息素浓度的函数数学表示为

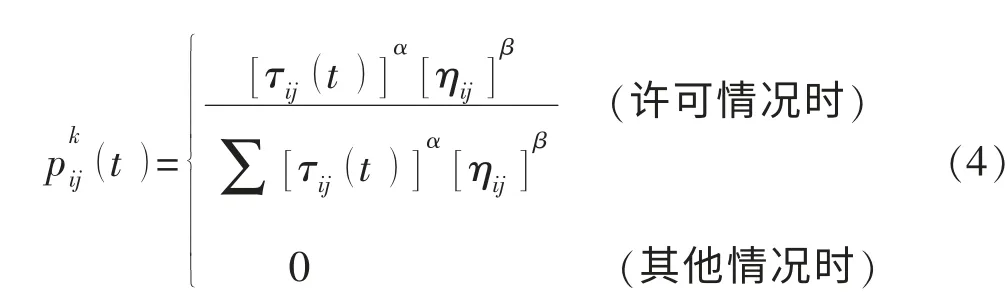
式中：τij（t） 为当前时刻信息素的值；ηij为在井口i 选择靶点j 的启发信息，数值为第i 井口到第j 靶点水平投影距离的倒数；α，β 分别为信息素和启发信息的相对重要性，为非负数。

在蚂蚁走完全程后，要对路径上的信息素进行更新，为后续蚂蚁提供指导。用参数ρ（0≤ρ≤1） 表示信息素的保留程度，在经过m 个时间单位后，各路段上的信息素要根据以下公式做调整。

式中：Δτijt+（m） 为t 到t+m 时间段留下信息素浓度。

信息素的更新方式主要有3 种算法模型（Antquantity，Ant-density，Ant-cycle）。第1 个模型信息素的更新只与当前节点到下一个交叉点距离有关，而第2个模型信息素更新是个定值，本文应用Ant-cycle 模型，与循环的整体路径有关系。

式中：Q 为常量，在蚂蚁k 经过路径ij 后，信息素的增量是该常量与循环路径长Lk的比值。

1.2.3 惩罚函数设计

对于井口分配模型来说，在遵循各井口与其靶点水平投影连线为最小的同时，还要保证其水平投影不相交或尽量少相交。是否相交可通过式（1）和式（2）判断。在蚁群算法中，利用惩罚函数［13-15］控制信息素的更新，使有交点的分配方案被选中的几率降低，从而优选出最优的分配方案。

通过编写子程序，判定式（2），若有交点，ω=0.5，否则ω=1。

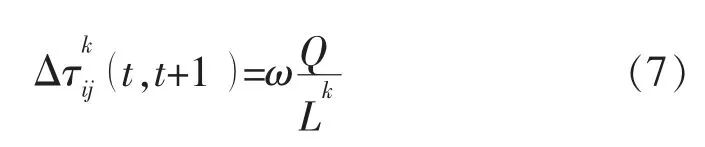
式中：ω 为惩罚因子。

2 基本求解步骤

用基本蚁群算法求解时要遵循2 个原则： 每个交叉点在地图上都可移动；各交叉点只能被访问一次。主要步骤如下：

1）铺设路网，以井口与靶点一一对应关系建立基本蚁群算法易解的路网模型。

2）令初始时间和循环次数均为0，路径上的信息素τij=c 或τij=0 且Δτij=0，最大循环次数为100。

3）于起始点取50 只蚂蚁，利用式（4）计算选择各路径的概率，并通过赌轮法选择下一个交叉点，根据式（1）、（2）判断是否惩罚，根据式（5）—（7）更新信息素。

4）判断蚂蚁是否都已到达目的地，若未完成，则重复步骤3）。

5）判断是否达到最大循环次数，若未达到，则重复步骤3），若已经达到最大循环次数，则输出最短路径路段组合信息。

3 实例计算

本文以大庆某丛式井为例，利用基本蚁群算法，对井口—靶点分配求解模型编制软件。井口坐标和靶点坐标见表1和表2。输入井口及靶点坐标，计算参数为：Q=100，C=10，α=0.5，β=1，ρ=0.7，惩罚因子ω=0.5。

表1 井口坐标

表2 靶点坐标

据此，在完成最大循环后，找到最优方案 （见图4）。可适当调整惩罚因子的值，目的是增加水平投影上有交叉点但工程实际中可行方案的几率。

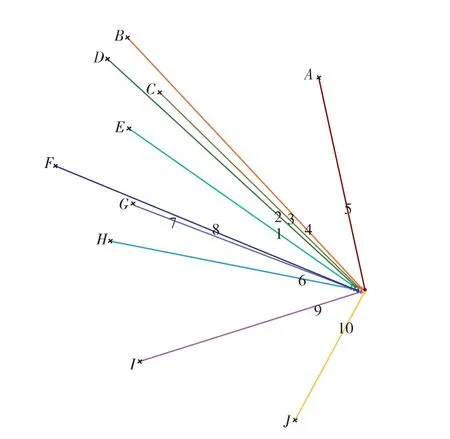
图4 井口分配

最优方案最终定为：1-E，2-D，3-C，4-B，5-A，6-H，7-G，8-F，9-I，10-J。

4 结论

1）构建蚁群算法求解丛式井井口分配模型，并引入惩罚函数，按照水平投影距离和最小并满足井口连接靶点的线段水平投影不相交或尽量少相交的原则，控制选中分配方案中带有交点方案的几率。该方法可快速准确地求解出最优方案。

2）引入惩罚机制的蚁群算法，求解丛式井井口分配模型，解出的分配方案满足现场施工要求。以此模型编制软件，能够快速有效地为设计人员提供切实可行的分配方案，提高工作效率。由于此模型只考虑了单井口对单靶点的情况，对于单井口多靶点的情况还需进一步研究。

［1］葛云华，鄢爱民，高永荣，等.丛式水平井钻井平台规划［J］.石油勘探与开发，2005，32（5）：94-100.

［2］陈祖锡，葛云华，周煜辉.用丛式井开发油田的方案设计［J］.石油钻采工艺，1992，14（6）：19-28.

［3］吴宏均，令文学，初永涛.吉林油田浅层丛式水平井井眼轨迹控制技术［J］.石油钻探技术，2011，39（5）：31-34.

［4］李绪锋.大组丛式井工程设计与施工［J］.西部探矿工程，2006（3）：74-77.

［5］史玉才，管志川，陈秋炎，等.钻井平台位置优化方法研究［J］.中国石油大学学报：自然科学版，2007，31（5）：44-47.

［6］朱文娟，喻高明，严维峰，等.油田经济极限井网密度的确定［J］.断块油气田，2008，15（4）：66-67，75.

［7］袁春华，张椿华，张茂林，等.B16 油藏helical 井网密度研究［J］.断块油气田，2010，17（1）：79-81.

［8］孙致学，苏玉亮，聂海峰，等.基于生产潜力的深水油田井位优化方法及应用［J］.断块油气田，2013，20（4）：473-476.

［9］王秀芝，石志良，龙胜祥，等.元坝气田开发经济合理井距研究［J］.断块油气田，2012，19（3）：123-127.

［10］郭永峰，朱江，齐恒之.优选海洋平台钻井方式［J］.中国海上油气：工程，2002，14（5）：22-24.

［11］李世勇，陈永强，李研.蚁群算法及其应用［M］.哈尔滨：哈尔滨工业大学出版社，2004：32-37.

［12］吴祈宗.运筹学与最优化方法［M］.2 版.北京：机械工业出版社，2003：186-190.

［13］张玉.基于改进蚁群算法的城市给水管网改扩建优化研究［D］.重庆：重庆大学，2007：30-41.

［14］李晓明，张烈辉，周宏，等.遗传算法在优化油田开发中的应用［J］.新疆石油地质，2005，26（1）：80-81.

［15］张志民，张小娟，李明华，等.一种引入奖励与惩罚机制的蚁群算法［J］.计算机仿真，2006，23（7）：161-163.