贝叶斯方法的污染源季节性排放量控制和管理

赵 英，郭 亮（1.哈尔滨工业大学市政环境工程学院，150090哈尔滨；2.城市水资源与水环境国家重点实验室（哈尔滨工业大学），150090哈尔滨）

贝叶斯方法的污染源季节性排放量控制和管理

赵 英1，2，郭 亮1，2
（1.哈尔滨工业大学市政环境工程学院，150090哈尔滨；
2.城市水资源与水环境国家重点实验室（哈尔滨工业大学），150090哈尔滨）

为保证水质功能区内水质达标，必须对区域内污染源排放量进行控制和管理.选取松花江哈尔滨段主要污染指标COD和氨氮为研究对象，利用一维水质模型构建各污染源排放量与河流水质之间的关系.用贝叶斯方法估计水质模型中的重要参数综合降解系数（k），根据估计时期的不同，分别建立季节模型和年度模型，用以控制既定水质目标下各污染源排放量.结果表明，季节模型的预测效果较好，能更好地表达水中污染物的综合降解浓度.应用季节模型和贝叶斯方法开展季节性水质管理工作，可以提供给决策者更多的信息，有助于对污染源排放量的不确定性进行量化和评估.此外，通过对比各污染源的削减水平，可得各污染源在不同时期的控制权重，从而使管理者在不同时期有针对性地对污染源排放量进行控制.贝叶斯方法在污染源排放量控制中的应用可以增强水质模型的预测能力，有效提高水质管理的水平.

贝叶斯方法；不确定性；污染源管理；季节模型；水质管理

水质功能区是为全面管理水污染控制系统，维护和改善水环境的使用功能而专门划定和设计的区域.通常由水域和排污控制系统两部分构成.建立水质功能区的目的在于使特定的水污染控制系统在管理控制上具有可操作性，使水环境质量及各种影响因素的信息得到有效的科学管理［1］.水质功能区内通常有多个污染源，若排入的污染物量超过了水环境承载力，下游水质就要恶化，因此，对于这些污染源排放量的科学管理是保证水质功能区内水质达标的必要手段.水质模型在水质管理中具有重要的作用［2-5］，利用水质模型可以判断污染物在水体中的扩散质量浓度，结合水质功能区水体的不同水质目标，可对污染源的排放量进行控制和管理.在水质管理中，水环境的不确定性是一个难题，严重制约着水质管理的准确性［6-7］.近些年，贝叶斯统计方法越来越多地应用到水环境不确定性问题研究中［8-12］，该方法的优势在于将水环境的不确定性问题转化成对模型参数的估计量，建立不确定性和估计概率之间的关联，以联合后验分布的数值代表不确定事件发生概率的大小.根据估计概率的大小，决策者可以对不确定性问题进行评估和判断，从而有针对性地开展水质管理工作.因此，该方法可以提高水质管理的准确度和有效性.

本文将贝叶斯方法与水质模型相结合，以污染较严重且季节性变化较明显的松花江哈尔滨段水质功能区为研究区域，利用水质模型建立该区域内多污染源与河流水质之间的关系，应用贝叶斯方法对水质模型中的重要参数污染物降解系数和污染物排放量（源强）进行估计，得出不确定性问题发生的概率分布，从而有针对性地加强对污染源排放量的控制和管理，制定季节性的水质管理方案，使河流水质得到提高.

1 研究方法

1.1 研究区域概况

松花江是我国黑、吉两省城市饮用水和流域内工农业生产赖以维系的主要水体［13］.松花江的主要干流流经哈尔滨市区，该市境内的大小河流大多属于松花江水系.降水主要集中在6～9月，占全年降水量的70%以上，冬季江面冰封期一般持续4个月以上［14］.近些年，随着人口的增加，大量污染物排入松花江，哈尔滨段水质污染严重，许多河段均不能达到黑龙江省环保局设定的水质目标，生态环境遭到破坏，对市民的生产和生活造成极大影响.因此，对沿岸污染源排放量的控制和有效管理是恢复松花江河流水质的重要措施.

松花江哈尔滨段的水质功能区有3个，分别为朱顺屯—东江桥、东江桥—大顶子山、大顶子山—依兰段.本文以覆盖市区且污染最为严重的东江桥—大顶子山功能区段为研究区域，此区段主要排污口分别为太平排污口、阿什河与呼兰河.太平排污口主要排放太平污水厂的处理废水，排放源强全年比较恒定；阿什河与呼兰河2个支流的水质大部分不达标，其中阿什河接受哈尔滨市区大部分的工业点源排放，而呼兰河是松花江最大的支流，年均流量达松花江干流的6%［15］.2支流的污染物质量浓度或源强较高，研究过程中将2支流概化为干流的排污口，由于这两条支流季节性变化均较明显，源强也呈现季节性变化特点.本研究以城市废水排放污染物特征为依据，选取能反映哈尔滨市河流水环境质量的主要污染指标氨氮和COD为研究对象.

1.2 河流水质模型

本研究区域东江桥—大顶子山水质功能区段共包含3个污染源，分别为太平排污口、阿什河与呼兰河，其中2支流概化为干流的排污口，3个排污口排出的污染物导致该水质功能区河段下游水质恶化，研究区域示意如图1所示.

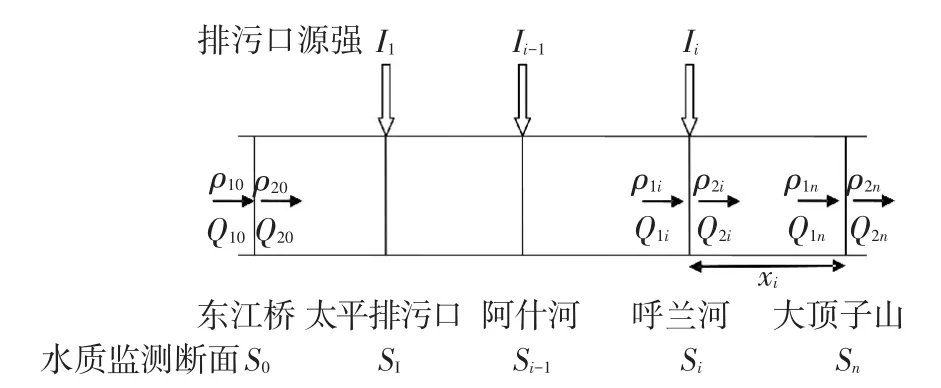
图1 松花江东江桥—大顶子山水质功能区概图

采用一维水质模型计算污染物扩散的质量浓度.假设污染物排出后在所在断面的横向和垂直方向上迅速混合均匀，每个监测断面上污染物质量浓度一致.如果忽略弥散作用，对每个排污口，一维水质模型可写成

式中：u为河段的平均水流速，m／s；ρ0为该排污口排出污染物后所在断面的污染物质量浓度，mg／L；ρ为河段下游距离排污口位置为x处污染物的质量浓度，mg／L；k为一阶降解系数，d-1.从图1可以看出，东江桥—大顶子山水质功能区被划分为4个部分，包含5个水质监测断面，即功能区上游、下游监测断面和3个排污口所在的监测断面.在上游和下游监测断面，污染物和水流量的关系为

在任意一个排污口所在的监测断面i，污染物源强、污染物质量浓度和河流水流量的关系可以表达为

因此，该水质功能区下游的污染物质量浓度为

式中：Qdown（Q2n）为河段下游水流量；ρupper（ρ10）为上游污染物质量浓度；Qupper（Q10）为上游水流量；I1、I2和I3为3个排污口排出的污染物源强；xi（i=0，1，2，3）为从排污口位置（Si）到下游断面（S4）的距离．通过式（5）可以建立水质功能区上游、下游污染物质量浓度和3个排污口排出的污染物源强之间的关系.假定上游污染物质量浓度已知，欲降低下游污染物质量浓度，达到既定的水质目标，通过控制3个排污口污染物的排放量即可实现.本研究应用贝叶斯方法实现对既定水质目标下污染源源强的估计和管理.

1.3 贝叶斯分析方法

近些年，贝叶斯分析方法越来越多地应用到解决环境问题中，提供了一种计算假设概率的方法.该方法是基于假设的先验概率、给定假设下观察到不同数据的概率以及观察到的数据本身而得出的.其方法为将关于未知参数的先验信息与样本信息综合，再根据贝叶斯公式得出后验信息，根据后验信息推断未知参数.

假设在时刻t观测到河段下游的污染物质量浓度为ρdown，t，则水质模型可以定义为

ρdown，t=f（xt；θ）+εt．（6）

式中：f（xt；θ）为模型在时刻t的输出值；xt为模型在时刻t的输入值（如上游污染物的质量浓度、各排污口源强和相关的水文参数等）；θ为未知参数集合；εt为误差项．应用贝叶斯原理可求得未知参数的后验分布，即

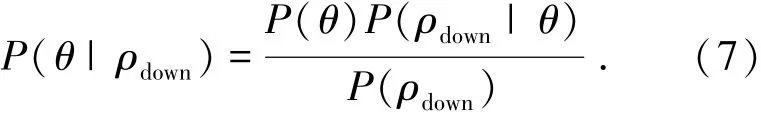
式中P（θ）为先验分布，来源于当前任何可得资料中信息的统计，P（ρdown｜θ）为似然函数，P（ρdown）为比例常数.采用Markov chain Monte Carlo（MCMC）抽样方法和Open BUGS软件实现贝叶斯方法，对未知参数进行估计.

1.4 季节及年度水质模型的建立

在水质模型中降解系数（k）是一个重要参数.水中污染物的稀释和降解是一个复杂多变的过程，降解系数反映了水体中污染物自净化的能力，受很多因素的影响，如水温、污染物质量浓度、河流水文条件和自然条件，因此，将k定义为综合衰减系数［16］.由于众多不确定因素对k的影响，且松花江季节性变化明显，导致其是一个动态变化的参数，在不同季节应具有不同的特征值.在以往的一维水质模型应用中，k一般在一年内都定义为固定值，以此建立的模型称为年度模型，该做法忽略了k的多变性，与实际情况不符.为提高水质模型应用的有效性，将一年分为3个时期，分别为冬季（1～3月和12月）、夏季（6～9月）和其他时期（4～5月和10～11月），对松花江各监测断面每个时期氨氮和COD的质量浓度进行统计，同时k值按照此3个时期分别进行估算，分别建立不同时期的水质模型，称为季节模型.下面介绍如何估计季节模型中的k，从而建立季节模型的框架.

将式（5）代入式（6），得

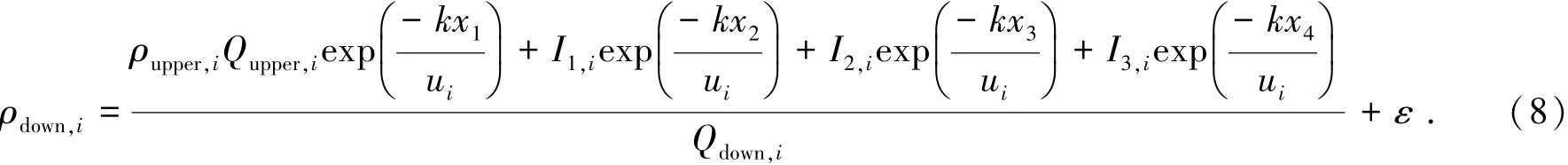
式中ε为正态分布误差项，平均值为0，方差为σ2．假定估计参数为正态分布，误差项独立，则待估参数综合衰减系数k的似然函数为

式中n为观测值的数量，σ2为方差，其余参数为实际测量值.实际测量值为水质监测断面处的月检测值，时间为2005～2010年，共72组数据.若建立季节模型，则式（9）中n为24，按3个时期分别输入样本，估计每个时期的k值，以不同的k值分别建立3个时期的季节模型；若建立年度模型，则n为72，估计出唯一的年度k值，以此建立年度模型.

2 结果及讨论

2.1 季节及年度模型的实现

根据上述建模方法分别对氨氮和COD的季节模型和年度模型中的k值进行估计，结果如图2所示.

图2 氨氮和COD年度模型和季节模型中k值的后验分布

水温和流量是综合衰减系数的主要影响因素.水温越高、流量越大，污染物降解速度越快，河流综合衰减系数越大［17］.因此，图2中估计的k值呈现季节性变化，夏天值最高，冬天值最低.

2.2 模型测试

采用季节模型和年度模型分别预测下游河流水质，模型测试中应用的k值为上节估计的平均值、5%和95%置信水平值.将模型预测结果和实测结果进行对比，检验模型的预测精度.同时，比较季节模型和年度模型的预测结果，考察两组模型的预测性能.测试数据为东江桥—大顶子山水质功能区段2011～2012年月检测数据，共计24组.针对氨氮和COD参数，分别将年度k值和季节k值代入模型公式（5），得到2组模型的预测结果，如图3、4所示.可以看出，在3个时期，氨氮的质量浓度呈现不同的分布特点.在同一时期，质量浓度变化较小；在不同时期质量浓度变化较大，且呈现季节性的变化规律，冬季最大，夏季最小.相对而言，COD的季节性变化不明显，数据变化的规律性差.计算预测值与实测值的MSE（均方误差）值判断模型的预测性能，氨氮和COD的年度模型和季节模型预测值与实测值MSE分析结果分别见表1、2.

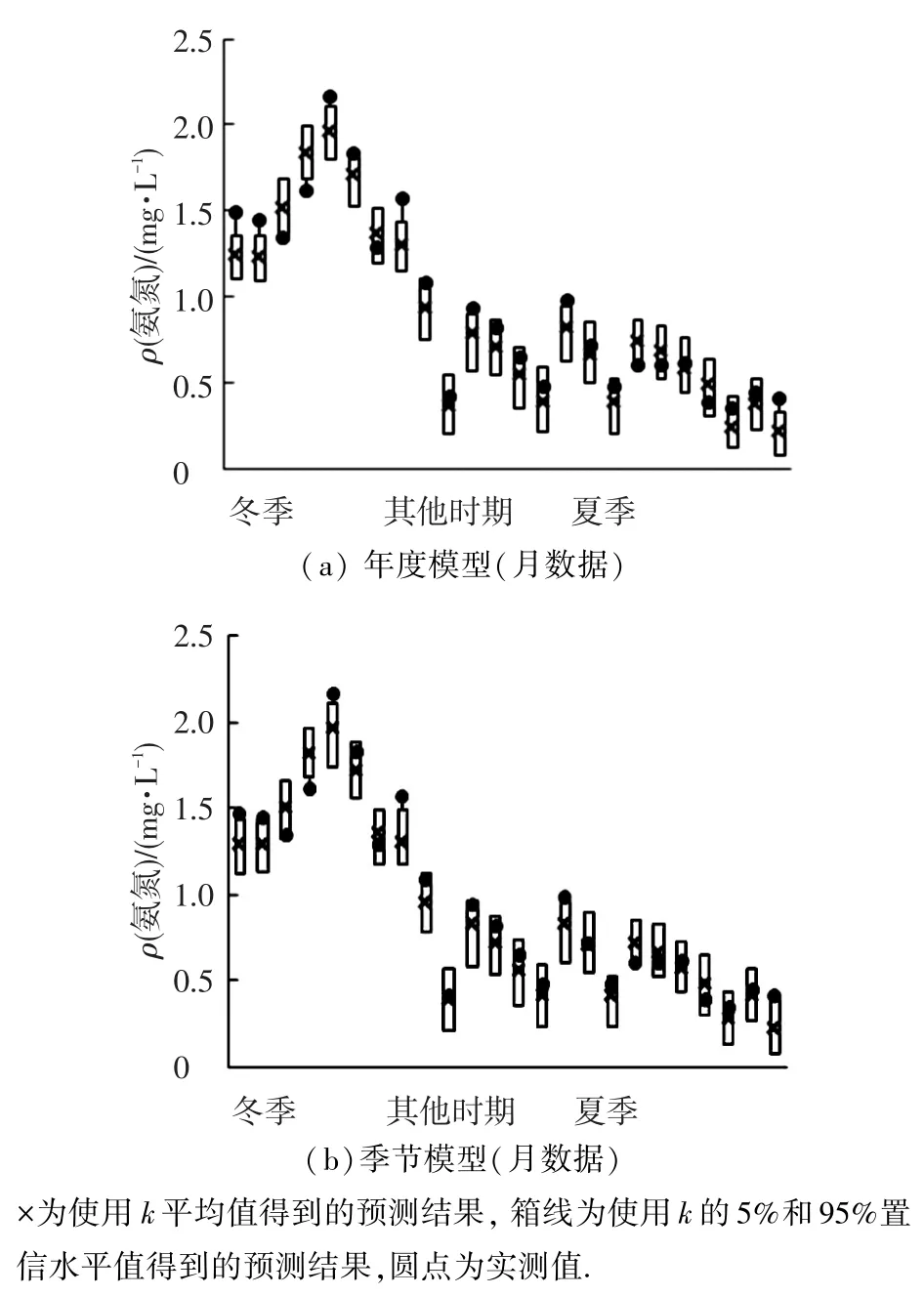
图3 氨氮的年度模型和季节模型预测值与实测值对比

图4 COD的年度模型和季节模型预测值与实测值对比

表1 氨氮年度模型和季节模型预测值与实测值MSE分析结果

表2 COD年度模型和季节模型预测值与实测值MSE分析结果

表3 东江桥—大顶子山水质功能区现氨氮水质标准及水质目标

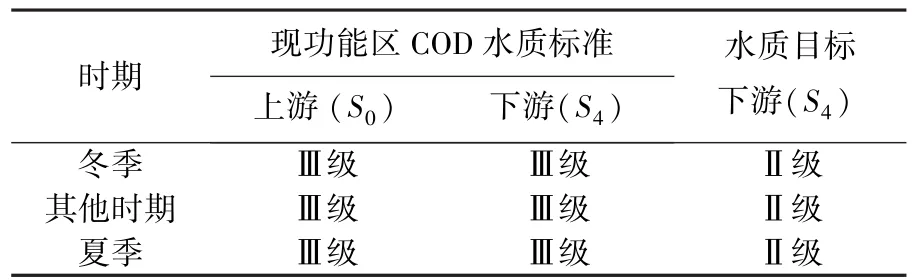
表4 东江桥—大顶子山水质功能区现COD水质标准及水质目标

从表1、2结果可以看出，总体来看年度模型和季节模型的预测效果均较好，其中应用k平均值的模型结构预测效果最好.因此，在实际应用中，为了计算方便，可以使用估计的k平均值建立水质模型.在氨氮模型中，显然季节模型的MSE值小于年度模型，说明季节模型具有更好的预测效果；在COD模型中，年度模型与季节模型的预测效果差异不大，季节模型略好，这应该与COD季节性变化规律不强密切相关.对处于我国北方的松花江，多年的监测数据表明氨氮的确具有规律的季节性变化，而COD的规律变化性较弱［18］.氨氮的质量浓度受外界影响的因素比COD少，在此区域氨氮主要来源于农业面源污染，因此，氨氮主要受农业面源污染、降雨、河流流量和水温等因素的影响，受人为影响的因素较少.而这些影响因素均具有明显的季节性变化特点，因此，氨氮的质量浓度也呈现出规则的季节性变化趋势；COD的变化由多方面因素导致，相比氨氮受人为的影响较多，因此较为复杂，而诸多影响因素又没有明显的规律可循，导致COD呈现变化的不规律性.由于COD季节性变化规律不强，季节性特点很难获取，以此建立的季节模型在预测中的优势就不明显，这是导致季节模型预测精度与年度模型接近的一个重要因素.而氨氮的季节性分布特点明显，从季节性数据中总结的规律准确率高，以此建立的季节模型具有较高的预测精度，明显优于年度模型.总体来看，根据水质参数的特点，分时期建立水质模型用于实际的水质管理中的方法是可行的.

3 模型的应用

在东江桥—大顶子山水质功能区段，由于3个污染源排放的污染物超标，导致该功能区下游水质变差，目前氨氮和COD的所属标准如表3、4所示.为了提高下游水质，必须削减各污染源污染物的排放量.现假定下游水质标准（见表3，4），应用贝叶斯方法估计各污染源污染物排放量的削减水平.

在估计源强I时，似然函数仍为式（9），只是式中k为已知值，为图3和图4中的估计结果，而I为待估计值.由于季节模型比年度模型具有更好的预测效果，估计源强时选用季节模型.假设式（9）中下游氨氮和COD为表3、4中水质目标，利用k平均值和季节模型估计I值，求得不同时期下各污染源的输出值和削减量，结果分别见表5、6.

与以往方法相比，表5、6中的结果可以提供给决策者更多的信息.首先，在不同时期既定水质目标下，可以获得每个污染源排放量的大小及参照历史值需要削减量的多少，包括排放量和削减量在不同概率下的数值（平均值、25%和75%置信水平值、5%和95%置信水平值），帮助决策者对污染源排放量的不确定性进行量化和评估.此外，从对比3个污染源排放量和削减量的结果中，可以获得每个时期对各污染源控制力度的权重，如由表5各污染源氨氮的削减量中可知，I2和I3污染源是造成下游河流氨氮超标的主要因素，在夏季主要的控制目标为I3，因为其削减量最大，冬季重点控制目标变为I2；在其他时期，由于水质目标较高，必须对3个污染源，尤其是I2和I3大力控制，才能达到要求．由表6各污染源COD削减量得出同样结论，I2和I3污染源是造成下游河流COD超标的主要因素，需要重点控制．夏季主要以削减I3为主，在冬季和其他时期主要削减I2，而I1由于全年排放量比较恒定，削减量在各个季节变化不大，均属次要影响源．根据上述分析结果，决策者可以制定季节性管理方案，有针对性地对污染源排放量进行控制．

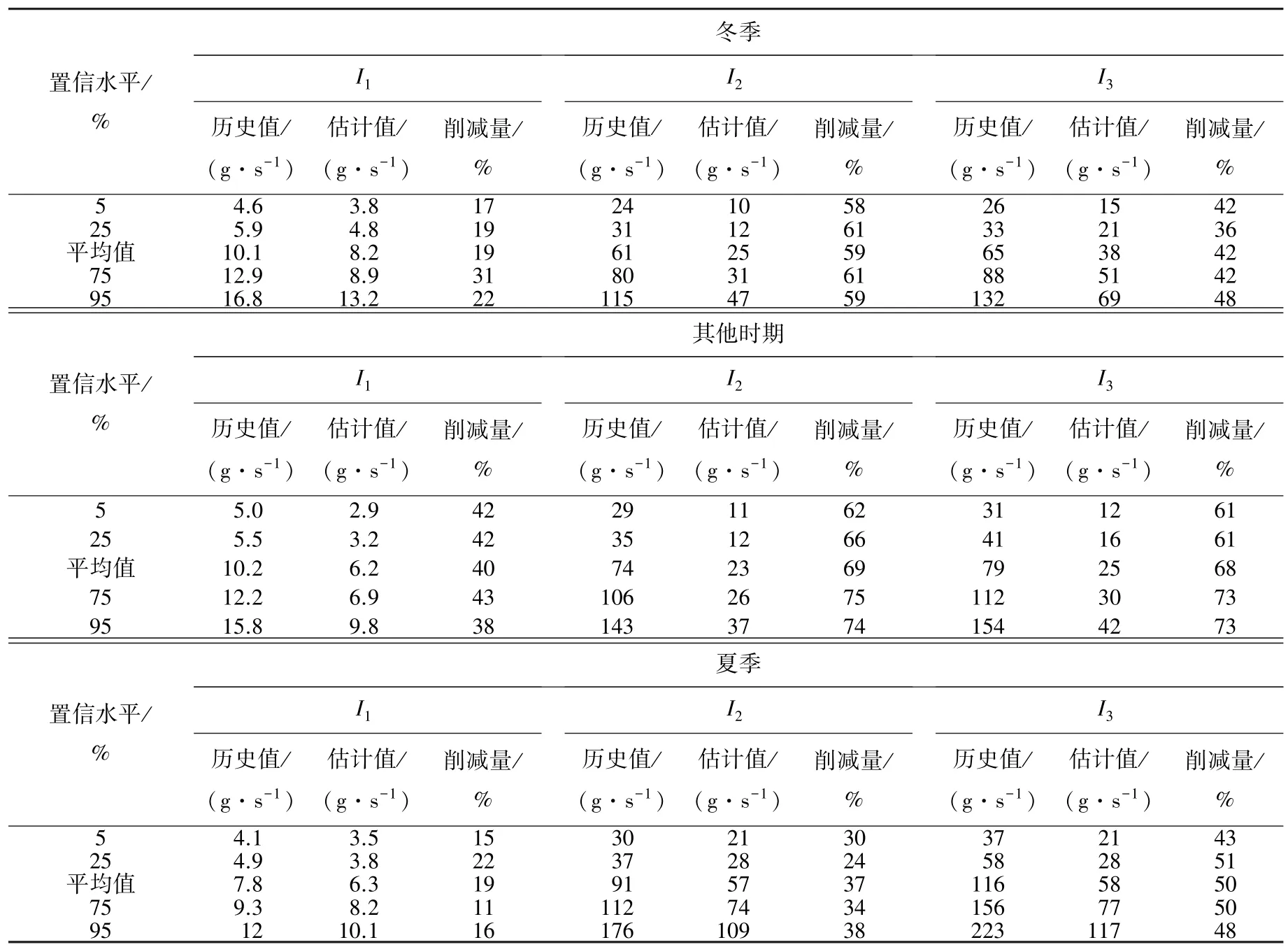
表5 东江桥—大顶子山水质功能区各时期氨氮排放量源强的历史值、估计值及削减量

表6 东江桥—大顶子山水质功能区各时期COD排放量源强的历史值、估计值及削减量

4 结 论

1）将贝叶斯方法引入到水质模型中，分别建立季节模型（k值按季节建立）和年度模型（k值在一年内恒定），用以控制既定水质目标下各污染源排放量.对于季节性变化明显的氨氮，季节模型的优势明显，而对于季节性变化规律不强的COD，季节模型的优势不明显.但总体来说，季节模型能更准确地表达各污染源和下游水质之间的关系，在实际水质管理中更加有效.

2）在研究区域河段下游水质达到既定标准时，各污染源排放量均需削减.对于氨氮，太平排污口、阿什河和呼兰河冬季的平均排污削减率为19%、59%和42%；其他时期的平均削减率为40%、69%和68%；夏季的平均削减率为19%、37%和50%.阿什河和呼兰河是造成下游河流氨氮超标的主要因素，在夏季主要的控制目标为呼兰河，因为其削减量最大；而在冬季重点控制目标变成了阿什河；在其他时期，由于水质目标较高，必须大力控制3个污染源才能达到要求.

3）对于COD，太平排污口、阿什河和呼兰河冬季的平均排污削减率为25%、57%和42%；其他时期的平均削减率为20%、48%和36%；夏季的平均削减率为17%、34%和43%.阿什河和呼兰河是造成下游河流COD超标的主要因素，需要重点控制.在夏季主要以削减呼兰河为主，冬季和其他时期主要削减阿什河，而太平排污口由于全年排放量比较恒定，削减量在各个季节变化不大，均属次要影响源.根据上述分析结果，决策者可以制定季节性管理方案，有针对性地对污染源排放量进行控制.

［1］中国环境保护部.松花江流域水污染防治“十二五”规划编制大纲［Z］.2010.

［2］QIN X S，HUANG G H，CHEN B，et al.An intervalparameter waste-load-allocation model for river water qualitymanagement under uncertainty［J］.Environment Management，2009，43：999-1012.

［3］SAADATPOUR M，AFSHAR A.Waste load allocation modeling with fuzzy goals simulation eoptimization approach［J］.Water Resource Management，2007，21：1207-1224.

［4］盛虎，向男，郭怀成，等.流域水质管理优化决策模型研究［J］.环境科学学报，2013，33（1）：1-8.

［5］王成金，段志国，魏丽娜.基于水质模型的污染监控预警和应急管理研究［J］.北方环境，2013，29（5）：54-58.

［6］ROBERTSON D M，SCHWARZ G E，SAAD D A，et al. Incorporating uncertainty into the ranking of SPARROW model nutrient yields from Mississippi／Atchafalaya River basin watersheds［J］.American Water Resource Association，2009，42：534-549.

［7］孙泽萍，付永胜.不确定性方法耦合水质模型研究综述［J］.环境科学与管理，2013，38（4）：68-70.

［8］黄凯，张晓玲.贝叶斯方法在水环境系统不确定性分析中的应用述评［J］.水电能源科学，2012，30（9）：47-49.

［9］罗建男，卢文喜，陈社明，等.基于贝叶斯网络的水环境管理研究［J］.节水灌溉，2011，3：68-72.

［10］PATIL A，DENG ZQ.Bayesian approach to estimating margin of safety for total maximum daily load development［J］.Environment Management，2011，92：910-918.

［11］ALAMEDDINE I，QIAN S S，RECKHOW K H.A Bayesian changepoint-threshold model to examine the effect of TMDL implementation on the flow-nitrogen concentration relationship in the Neuse River basin［J］. Water Research，2011，45：51-62.

［12］FAULKNER B R.Bayesianmodeling of the assimilative capacity component of nutrient total maximum daily loads［J］.Water Resource Research，2008，44：W08415.

［13］高鹏飞，王鹏，郭亮，等.流域水污染应急决策支持系统中模型系统研究［J］.哈尔滨工业大学学报，2009，41（2）：92-96.

［14］赵英，郭亮，王鹏.数据挖掘技术在松花江水质预测中的应用［J］.哈尔滨工业大学学报，2011，43（10）：1569-1575.

［15］王祎，李静文，邵雪，等.基于计算智能的流域污染排放优化模式研究［J］.中国环境科学，2012，32（1）：1943-1950.

［16］沈万斌，朱晓娟，高凯，等.吉林省松花江干流化学需要量（COD）和氨氮环境容量特征［J］.科学技术与工程，2013，13（23）：1671-1815.

［17］陈丁江，吕军，金树权，等.河流水环境容量的估算和分配研究［J］.水土保持学报，2007，21（3）：123-127.［18］哈尔滨环境保护局.2005—2012年哈尔滨环境质量公报［R］.哈尔滨：哈尔滨环境保护局，2013.

（编辑 刘 彤）

A seasonal management method for controlling pollution sources discharge based on Bayesian method

ZHAO Ying1，2，GUO Liang1，2
（1.School of Municipal and Environmental Engineering，Harbin Institute of Technology，150090 Harbin，China；2.State Key Laboratory of Urban Water Resource and Environment（Harbin Institute of Technology），150090 Harbin，China）

Ammonia and COD are selected as study variables for they are the main water quality parameters and can representwater environment quality of the Harbin City Reach of the Songhua River.One-dimensional water quality model is used to set up the relationship of pollutant loadings and water quality.The comprehensive decay rate（k），a key parameter ofwater qualitymodel，is estimated by Bayesianmethod.The seasonalmodel and annualmodel are respectively set up according to different k estimated in different period. The pollutant loadings are controlled by themodels for downriver water quality can meet targeted goals.From contrasting the twomodels，it indicates that predicting precision of seasonalmodel is high than annualmodel for seasonal model can better express comprehensive degradation concentration of ammonia in water. Contrasting with othermethods，water qualitymanagementwith seasonalmodel can offer decision makersmore useful information，and help them address uncertainties.In addition，influencingweights of the three pollution sources can be obtained by contrasting load reduced ratios.The information could inform decisionmakers of the required load reductions for the three time periods.

Bayesian；uncertainty；pollution sources controlling；seasonalmodel；water quality management

X703.5

A

0367-6234（2014）12-0026-07

2014-06-03.

国家自然科学基金青年基金（71203041）；中国博士后科学基金（20110491056）；黑龙江省博士后基金（LBH-Z10172）；哈尔滨工业大学创新基金（2011年）.

赵 英（1978—），女，讲师.

郭 亮，guoliang0617＠hit.edu.cn.