基于多变量加权一阶局域法多步预报模型的舰船摇荡预报

蔡烽，刘博，石爱国

基于多变量加权一阶局域法多步预报模型的舰船摇荡预报

蔡烽a，刘博b，石爱国a

（海军大连舰艇学院a.航海系辽宁大连；b.研究生管理大队，辽宁大连116018）

针对舰船各个自由度摇荡之间存在耦合的实际，提出了一种多变量加权一阶局域法多步预报模型（MAOLMM）。对Chen’s吸引子仿真数据及某型船真实海浪下航行的摇荡数据进行了预报分析，结果显示，多变量加权一阶局域法多步预报模型的预报精度高于单变量加权一阶局域法多步预报模型，提高了舰船摇荡预报的有效性。关键词：时间序列；舰船摇荡；多变量；加权一阶局域法多步预报

1 引言

舰船摇荡预报可以有效提高舰船作战使用的海情，为舰载机起降及武备使用等提供有效保障[1]。相关研究表明，舰船摇荡运动具有混沌特性[1-5]，可以用加权一阶局域法等模型进行预报[1，4]。而舰船各个自由度的摇荡运动之间存在耦合，如果只用单变量的数据进行预报，则不能充分反应摇荡运动的实际动力学特性。为此，本文提出了多变量加权一阶局域法多步预报模型，可以同时对舰船多个自由度的摇荡运动进行预报。

2 多变量时间序列相空间重构参数的确定[6]

2.1 延迟时间的确定

因为延迟时间是与每个变量相关，故可采用单变量延迟时间的确定方式对多变量预报法中每一变量单独确定延迟时间。

延迟时间选择的原则为使YM与YM+τ具有某种程度的独立但又不完全无关，使其能在重构的相空间中作为独立的坐标处理。比较常用的方法有自相关函数法和平均互信息法。

2.2 嵌入维数的确定

利用虚假最近邻点确定嵌入维数[7]。设两变量重构的相点为：

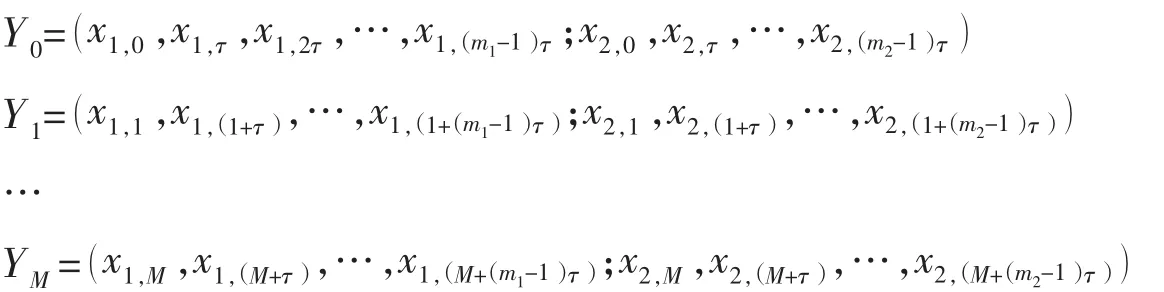
设参考点YM的最近邻点为Yη（n），当维数从ml增加到ml+1，则此两点的距离为大很多，可以认为是由于高维吸引子中两个不相邻的点在投影到低维轨线上时变成相邻的两点造成的，因此这样的邻点是虚假的。通过循环迭代计算，可以确定最适合的嵌入维数m1，m2，…，mL。

3 多变量加权一阶局域法多步预报模型[1，4，8]

以两变量为例推导多变量加权一阶局域法多步预报模型（Multivariate Add-weighted One-rank Local-region Multi-steps Method,MAOLMM）如下。设两变量重构的相点为：

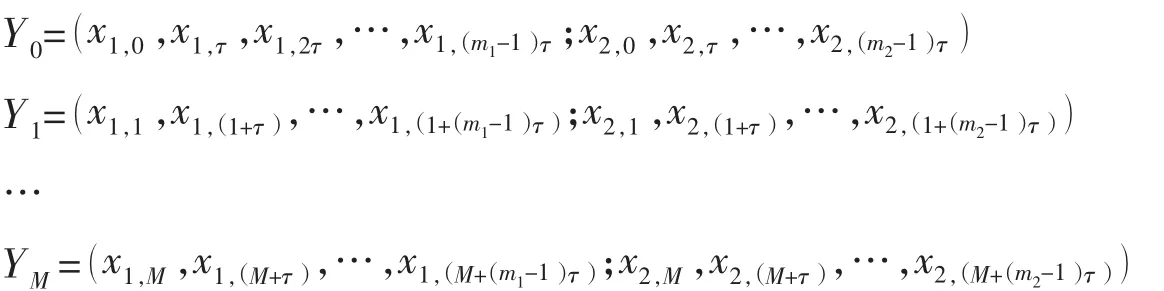
设YM的参考向量集｛YMi｝，i=1，2，…，q（ q=m+1，m=m1+m2），其演化K步后的相点集为｛YMi+K｝，则一阶局域线性拟合为：

根据加权最小二乘原理，有：

对上式分别对ak，bk求偏导，得：

化简，

其中：

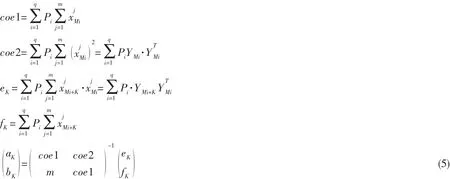
写成矩阵形式为：

根据求得的aK、bK，代入K步预测公式YˆM+K=aKe+bKYM，即可得到演化K步后的相点预测值YˆM+K。其中：YˆM+K中的第M个元素分别为两个变量的K步预测值。

4 算例分析

因为每段数据的震荡幅度不同，为使预报值与真实值的差值具有比较统一的衡量标准，故采用相对误差作为比较标准。因为采样频率为10 Hz，故对每10个预报点求出预测值与真实值的差值的平均值作为此秒的绝对误差。将求出的绝对误差再除以该段数据的摇荡最大幅值并用百分数表示作为此段数据的相对误差。

其中：xˆi为预测值，xi为真实值，n=1，2，…，15。预报分为20段进行，对每段进行误差计算，然后对每一步长计算平均值以消除特例预报段的影响。

4.1 Chen’s吸引子

美国休斯顿大学陈关荣教授在研究混沌反控制的过程中发现了一个新的混沌吸引子，它是由如下三维系统产生的[9]：

取初值x（0）=1，y（0）=0，z（0）=0；积分时间步长h=0.001。。用四阶Runge-Kutta法积分上述方程组得到50 000个点数据作为测试样本，取x，y序列进行预报分析。评价预报效果所采用的指标为绝对误差，即预报值与真实值的数量差。

此段x数据绝对值的最大值为30.397 7，平均值为7.139 6，y数据绝对值的最大值为36.205 6，平均值为7.654 5。

表1 Chen’s吸引子预报误差Tab.1 Chen’s data prediction error

4.2 Lorenz模型

1963年美国著名气象学家洛伦兹（E.N.Lorenz）在研究天气预报问题时，发现确定性方程中出现混沌现象。方程为：

取初值为x=1，y=0，z=0.1；积分时间步长h= 0.002。用四阶Runge-Kutta法积分上述方程组得到50 000个点数据作为测试样本，取x，y序列进行预报分析。评价预报效果所采用的指标为绝对误差，即预报值与真实值的数量差。

零均值化之后，该段数据的第一维幅值平均值为11.364 5，最大值为46.625 8，第二维幅值平均值为11.052 5，最大值为41.488 4。

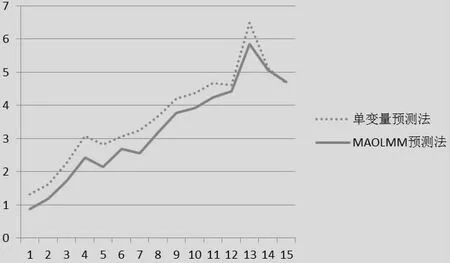
图1 Chen’s吸引子预报误差对比Fig.1 Comparison of Chen’s data prediction error

表2 Lorenz模型预报误差Tab.2 Lorenz data prediction error

图2 Lorenz数据预报误差对比Fig.2 Comparison of Lorenz data prediction error

图3 顶浪18 kns某型船摇荡数据预报误差对比Fig.3 Comparison of 18 kns(right)top sailing data prediction error

4.3 某型船真实海浪下摇荡数据预报

采用的是某型船真实海浪情况下顶浪18 kns航行的摇荡数据，采样频率10 Hz。此组数据横摇幅值最大值为2.495 1，横摇幅值平均值为0.692 5。纵摇幅值最大值为3.727 0，纵摇幅值平均值为0.918 7。此处以横摇预报为例。

表3 某型船顶浪18 kns航行摇荡预报误差Tab.3 Sway data prediction error of some ship with a speed of 18 kns

5 结论与展望

上述仿真表明，多变量加权一阶局域法多步预报模型的预报精度优于单变量加权一阶局域法多步预报模型，预报精度可以提升15%～25%，从而提高了舰船摇荡预报的有效性。从仿真测试中参数的选取情况来看，多变量时间序列的嵌入维数及延迟时间的选取并不是越大越好，还要注意各维数的相对大小关系。

[1]蔡烽.提升舰船作战使用海情关键技术研究[D].大连:海军大连舰艇学院,2004.

[2]陈予恕,张伟.船舶横摇运动的全局分岔和混沌动力学[J].现代数学和力学－Ⅵ,1998:455-459.

[3]欧阳茹荃,朱继懋.船舶横摇运动的非线性振动与混沌[J].水动力学研究与进展,1999,14(3):334-340.

[4]蔡烽,万林,石爱国.基于相空间重构技术的舰船摇荡极短期预报[J].水动力学研究与进展A辑,2005,20(6): 780-784.

[5]Hou Jianjun,Cai Feng,Shi Aiguo,et al.Chaotic dynamics analysis of ship motions[C]//Proceedings of the AsiaLink-EAMARNET International Conference on Ship Design,Production&Operation.Harbin,China,2007:502-506.

[6]王海燕,卢山.非线性时间序列分析及其应用[M].北京:科学出版社,2006.

[7]Cai Minglun,Cai Feng,Shi Aiguo,Zhou Bo,Zhang Yongsheng.Chaotic time series prediction based on local-region multi-steps forecasting model[C]//In:IEEE International Symposium on Neural Networks(ISNN).Dalian,China,2004.

[8]陆君安,吕金虎,陈士华.Chen’s混沌吸引子及其特征量[J].控制理论与应用,2002,19(2):308-310.

[9]薛洁妮,史忠科.基于混沌时间序列分析法的短时交通流预测研究[J].交通运输系统工程与信息,2008,8(5):68-72.

[10]汪斌,周辉.基于相空间优化近邻点的跳频预测方法研究[J].装备指挥技术学院学报,2007,2(18):85-88.

Ship motions’prediction based on multivariate add-weighted one-rank local-region multi-steps method

CAI Fenga,LIU Bob,SHI Ai-guoa
(a.Dept.of Navigation;b.Company of Postgraduate Management,Dalian Naval Academy,Dalian,116018,China)

A model of Multivariate Add-weighted One-rank Local-region Multi-steps Method(MAOLMM) is proposed aiming at various degrees of freedoms for ships’actual coupling effect.A forecast test is operated with Chen’s simulation data.Simulation results show that the precision of Multivariate Add-weighted One-rank Local-region Multi-steps Method is better than Single Add-weighted One-rank Local-region Multi-steps Method(SAOLMM).And it raised the effectiveness of predicting ship motions.

time series;ship motions;multivariate;AOLMM(add-weighted one-rank local-region multi-steps method)

U661.32

A

10.3969/j.issn.1007-7294.2014.07.008

1007-7294（2014）07-0794-05

2014-03-07

国防预研基金；国家自然科学基金资助（61071006）

蔡烽（1973-），男，博士，海军大连舰艇学院航海系副教授，E-mail：vipcaif@tom.com；刘博（1986-），男，硕士。