水下航行体垂直发射尾空泡生成演化过程三维数值研究

权晓波，燕国军，李岩，孔德才，李明

水下航行体垂直发射尾空泡生成演化过程三维数值研究

权晓波，燕国军，李岩，孔德才，李明

（北京宇航系统工程研究所，北京100076）

为研究水下航行体垂直发射尾空泡生成演化过程，采用Mixture多相流模型、标准k-ε湍流模型和动网格方法求解RANS方程，建立了三维三自由度计算模型，对航行体垂直发射过程进行了数值模拟，计算结果与试验结果吻合较好，获得了尾空泡生成演化的周期性特征。研究了牵连速度和发射水深对尾空泡生成演化的影响，结果表明，牵连速度增大导致拉断后回射流上升斜切尾空泡的角度增大；发射水深增加导致尾空泡压力增大，振荡周期缩短。

水下航行体；尾空泡；动网格；牵连速度；发射水深

1 引言

目前水下平台垂直发射航行体大多采用冷发射，即利用高压燃气将航行体弹射出筒，然后航行体依靠惯性穿越水面，发射过程可分为三个阶段：出筒段、水中航行段和出水段。这种发射方式在航行体尾出筒后，发射燃气会在航行体尾部形成空泡，这一空泡不断拉长，直至拉断并形成回射流。航行体尾出水后，尾空泡与大气连通，空泡底部水体急剧上升形成尾涌现象[1]。水下平台发射航行体时需保持一定的航行速度以保证其操纵性，因此航行体出筒时不仅具有垂直方向速度，而且具有横向牵连速度。航行体的牵连运动破坏了流场的对称性，使得航行体出筒后俯仰姿态逐渐增大，这将对尾空泡的生成演化过程产生较大影响。

尾空泡的生成演化过程涉及到高温高压的燃气、水体和大气等多种流体介质，而且航行体的位置和姿态不断变化，是一个复杂的非定常多相流问题，目前采用多相流模型和动网格方法的数值模拟已成为重要的研究手段之一。多相流模型根据界面处理的不同大致可分为两类，一类是自由界面追踪模型，如VOF[2]、MAC[3]模型，可以处理自由界面变化较剧烈但界面基本清晰的流动问题，另一类是混合模型，如Mixture模型等，可模拟各相之间强烈掺混、界面基本不清晰的流动问题。Dyment等[4]采用VOF模型对尾空泡的形成与发展进行了数值模拟；刘志勇等[5]采用改进的MAC方法二维轴对称模拟了尾空泡从生成至拉断的过程；张红军等[6]采用Mixture模型对尾空泡的生成演化过程进行了考虑横流速度的三维一自由度数值模拟。

本文采用Mixture模型、标准k-ε湍流模型和动网格方法求解非定常RANS方程，对水下航行体的垂直发射过程进行三维三自由度非定常数值模拟，获得了尾空泡的生成演化特征，在相同条件下比较分析了牵连速度和发射水深对尾空泡生成演化过程的影响。

2 计算模型

本文采用Mixture模型模拟气液两相流动，忽略相间的滑移速度，计算中设定水体为不可压缩相，气体为可压缩相。采用有限体积法离散控制方程，结合Simple算法来求解。

2.1 流体控制方程

1）连续性方程

2）动量方程

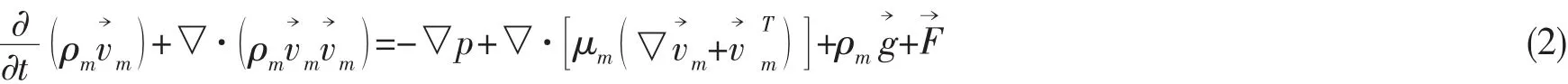
3）能量方程

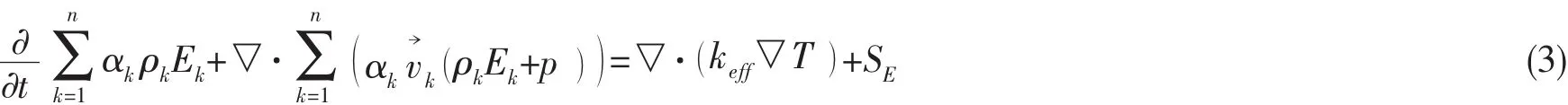
4）次相体积分数方程

5）状态方程

2.2 航行体动力学方程

本文中视航行体为刚体，尾出筒后开始计算其俯仰运动（忽略出筒过程的俯仰运动）。通过下式计算航行体质心的合力和绕质心的合力矩：

2.3 计算域、网格及边界条件

计算域包括发射筒、水域和大气域，考虑到几何和运动特征的对称性，建立半三维模型，如图1所示（图中未给出航行体头锥段外形）。发射筒底燃气入口为压力入口边界，尾出筒后改为壁面边界；水域和空气域外围均为压力出口边界。考虑到尾出筒后开始计算航行体的俯仰姿态，在航行体运动区域内划分非结构网格，采用当地重构法更新动网格，为保证航行体壁面附近网格质量，对航行体进行了包裹，该包裹域内网格不发生变化。

图1 尾出筒后计算域及网格示意图Fig.1 Schematic of computational field and grid after tube-exit

3 尾空泡生成演化特征

文章分析发射水深H、牵连速度U工况的尾空泡生成演化特征。为获得尾空泡压力时变历程，在航行体尾部布置了压力测点，如图2所示。测点压力计算值与试验值比较如图3所示，从中可以看出，计算值与试验值吻合较好；航行体尾部压力在尾出筒后至尾出水前经历了两次先下降后上升的振荡过程，尾出水后变为大气压。图4比较了航行体轴向速度的计算值与试验值，两者吻合良好，进一步验证了本文所建计算模型的合理性。应该说明的是，本文中压力p、时间t、轴向速度v分别以发射水深静压P、出筒时刻T、轴向速度最大值Vmax进行了无量纲化。

图2 航行体尾部测点位置Fig.2 Pressure monitoring point location on the vehicle’s tail

图3测点压力计算值与试验值比较Fig.3 Pressure comparison between calculated value and experimental value

图5 给出了典型时刻航行体尾部流场相图和压力云图，从图中可以看出，当航行体尾出筒后，筒内高压气体开始向外膨胀，且主要跟随航行体沿轴向膨胀；随着尾空泡体积的不断增大，泡内压力不断下降，当其压力低于环境水压时，外围水体开始向内挤压尾空泡，尾空泡发生颈缩，泡内压力开始上升，直至拉断形成附体尾空泡，此时外围水体相互撞击在空泡闭合处形成局部高压区域，如（a）～（c）所示。在高压的驱动下，尾空泡末端形成了上升斜切空泡的射流，而且受拉断高压影响，泡内压力超过了环境水压，尾空泡转而开始膨胀，泡内压力下降，如（d）所示；当泡内压力低于环境水压时，尾空泡又转而收缩，泡内压力上升，如（e）所示；当泡内压力大于环境水压时，尾空泡转为膨胀后出水，如（f）所示。航行体尾出水后，尾空泡与大气连通，水体从尾空泡底部上涌追赶航行体，如（g）、（h）所示。

图4 轴向速度计算值与试验值比较Fig.4 Axial velocity comparison between calculated value and experimental value

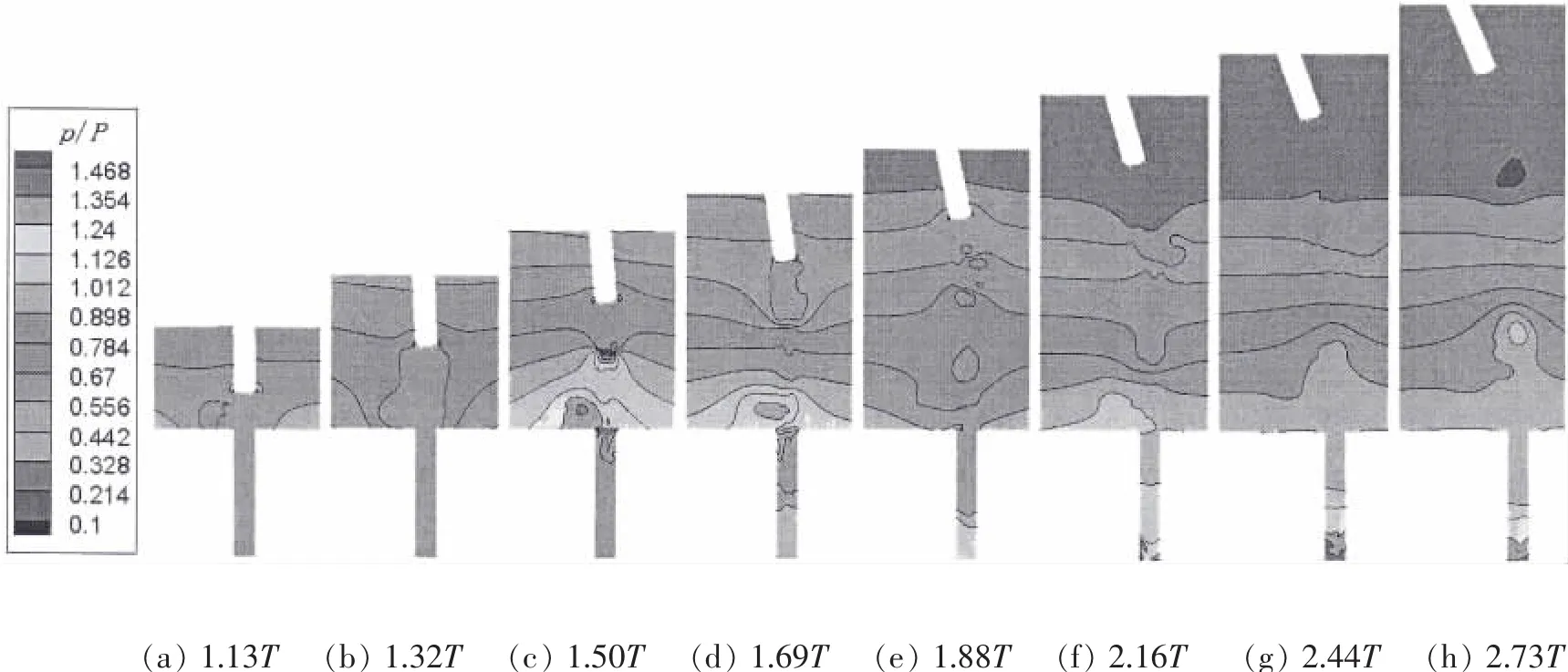
图5 尾空泡生成演化过程流场图Fig.5 Flow field graph of tail bubble evolution process

4 牵连速度影响分析

本章在相同发射深度H条件下，研究不同牵连速度（0.4U、0.7U、1.0U）对尾空泡生成演化的影响。计算获得的尾空泡压力曲线如图6所示，从中可以看出，不同牵连速度条件下，出水前尾空泡压力均经历了两次先下降后上升的振荡过程；尾空泡第一次压力振荡周期几乎完全一致，随着牵连速度的增加，第二次振荡周期压力逐渐减小。这说明了尾空泡膨胀、颈缩至拉断的过程是几乎一致的，牵连速度主要影响尾空泡的第二次膨胀收缩周期。

图7比较了不同牵连速度下尾空泡第二次压力振荡周期的典型时刻相图，从图中可以看出，不同牵连速度条件下，拉断形成的附体尾空泡体积相当；随着牵连速度增大，回射流上升斜切尾空泡的角度增大，对尾空泡压力的影响越小，因此第二次压力振荡周期下降得更快。

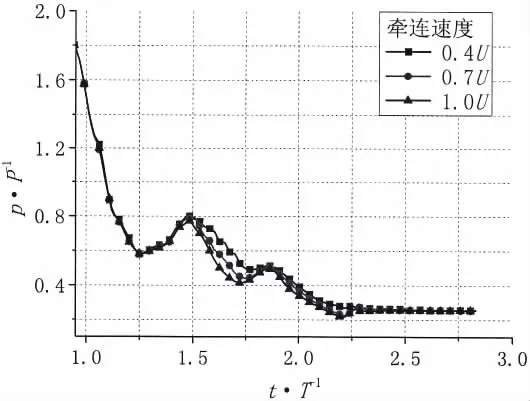
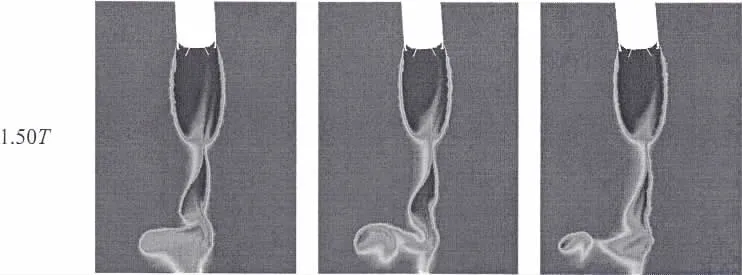
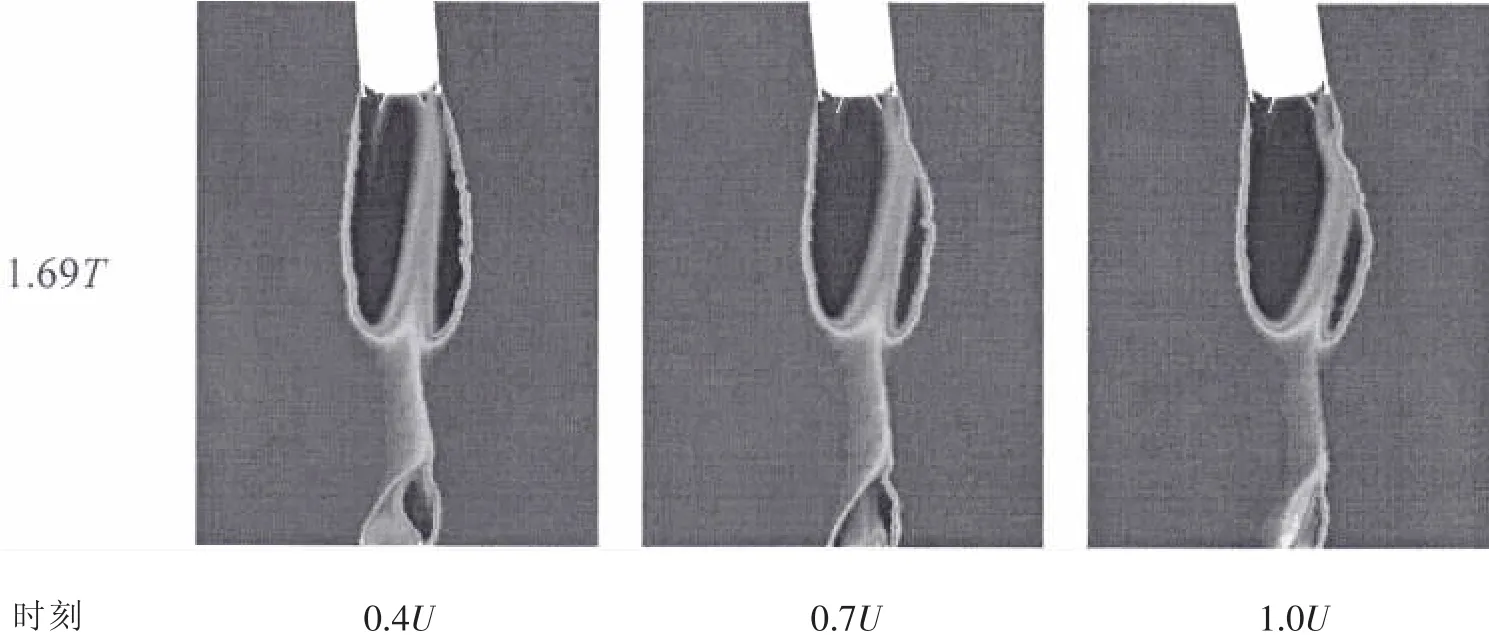
图7 不同牵连速度下典型时刻相图比较Fig.7 Typical phase diagram comparison among different transport velocity

5 发射水深影响分析

文章在相同牵连速度U条件下，研究不同发射水深（0.8H、1.0H、1.2H）对尾空泡生成演化的影响。计算获得的尾空泡压力曲线如图8所示，从中可以看出，不同发射水深条件下，出水前尾空泡压力均呈现周期性的先下降后上升的变化；随着水深增加，尾出筒后相同时刻航行体尾部的环境压力上升，尾空泡压力增大；水深的增加导致了尾空泡演化速度加快，压力振荡周期缩短，振荡次数增多。

图9比较了不同发射深度下尾空泡生成演化典型时刻的相图，从图中可以看出，随着水深增加，尾空泡发展速度加快，尾空泡拉断时间提前，尾空泡体积减小；拉断后形成的回射流斜切空泡的角度几乎一致，可见水深对回射流上升角度几乎没有影响。

图8 不同发射水深下尾空泡压力时变曲线比较Fig.8 Tail bubble pressure curve comparison among different launch water depth

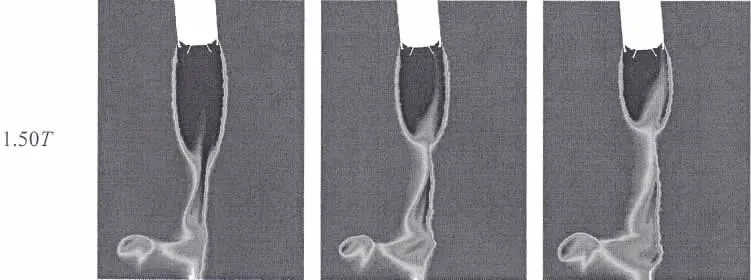
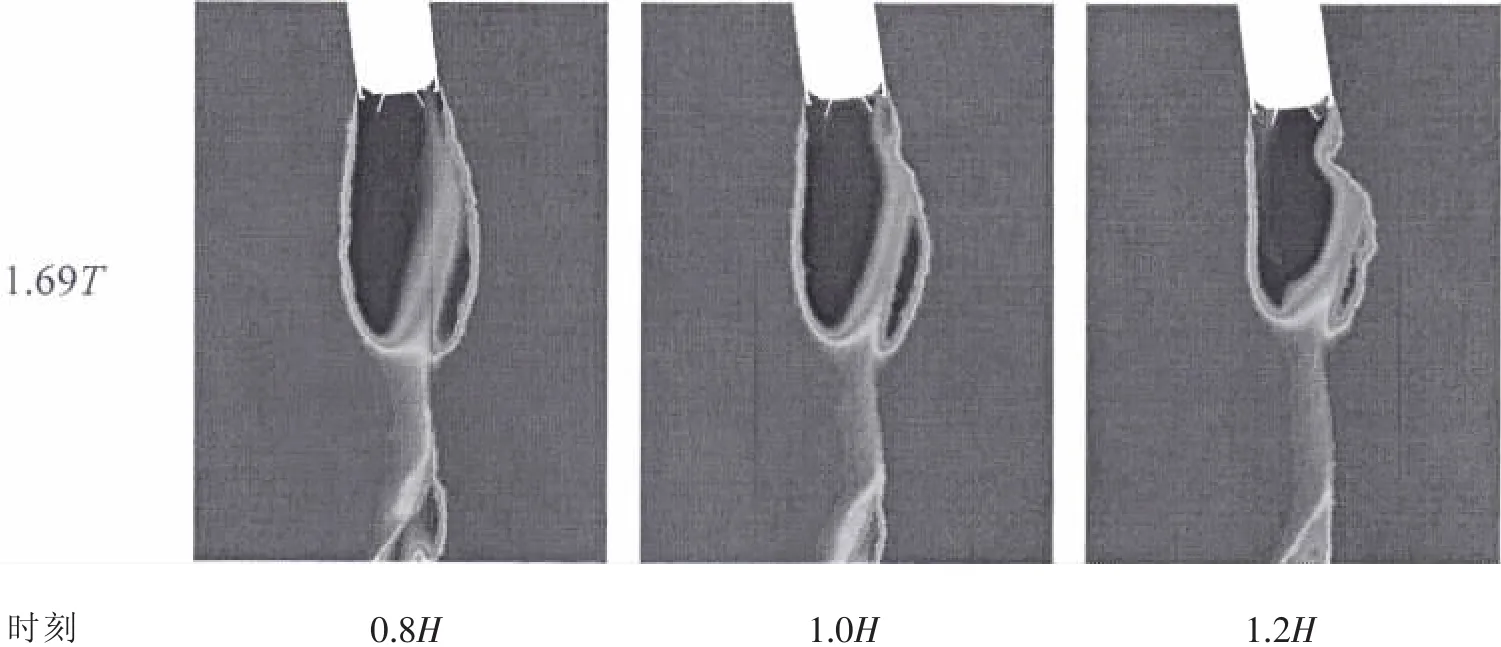
图9 不同发射水深下典型时刻相图比较Fig.9 Typical phase diagram comparison among different launch water depth

6 结论

本文采用均质多相流模型、标准k-ε湍流模型和动网格方法求解了非定常的RANS方程，对航行体水下垂直发射过程进行了三维数值模拟，得到的主要结论如下：

（1）基于Mixture模型和动网格方法实现了三维非定常多相流场和航行体运动的耦合计算，测点压力和航行体轴向速度计算值与试验值吻合较好，说明本文所建计算模型能较好地模拟尾空泡的生成演化过程。

（2）获得了尾空泡的生成演化特征：筒口高压气体膨胀、颈缩至拉断形成附体尾空泡，然后回射流上升斜切尾空泡，空泡继续周期性膨胀、收缩，直至出水后形成尾涌；尾空泡出水前压力呈现周期性的先下降后上升的振荡变化，直至出水后变为大气压。

（3）相同发射水深条件下，牵连速度主要影响尾空泡拉断后回射流的上升斜切空泡的角度，进而影响拉断后的泡内压力，随着牵连速度增加，拉断后泡内压力减小。

（4）相同牵连速度条件下，随着发射水深增加，尾空泡压力增大，演化速度加快，压力振荡周期缩短，而对拉断后回射流上升斜切空泡角度几乎无影响。

[1]黄寿康.流体动力·弹道·载荷·环境[M].北京:宇航出版社,1991.

[2]Hirt C W.Volume of fluid(VOF)method for dynamics of free boundaries[J].J Comput Phys,1981,39:201-225.

[3]Mckee S,Tome M F,Ferreira V G,et al.The MAC methond[J].Computers&Fluids,2008,37(8):901-930.

[4]Dyment A,Flodrops J P,Paquet J B,et al.Gaseous cavity at the base of an underwater projectile[J].Aerospace Science and Technology,1998,2(8):489-504.

[5]刘志勇,颜开,王宝寿.潜射导弹尾空泡从生成到拉断过程的数值模拟[J].船舶力学,2005,9(1):43-50.

Liu Zhiyong,Yan Kai,Wang Baoshou.Numerical simulation of the development process of a trailing cavity from generation to separation[J].Journal of Ship Mechanics,2005,9(1):43-50.

[6]张红军,陆宏志,裴胤等.潜射导弹出筒过程的三维非定常数值模拟研究[J].水动力学研究与进展A辑,2010,25 (3):406-415.

Three-dimensional numerical study on the evolution process of tail bubble of underwater vehicle vertical launching

QUAN Xiao-bo,YAN Guo-jun,LI Yan,KONG De-cai,LI Ming
(Beijing Institute of Astronautical Systems Engineering,Beijing 100076,China)

To study the evolution process of tail bubble of underwater vehicle vertical launching,Mixture model,standardk-εturbulence model and dynamic mesh method were adopted to establish 3DOF model to carry out numerical simulation of the vertical launching process,the calculation results agreed well with experimental results,the cyclical characteristics of the evolution process of tail bubble was acquired.The influences of transport velocity and launch water depth on the tail bubble evolution process were researched, the results show that the bigger transport velocity,the bigger re-entrant jet flow angle after tail bubble fractures;the bigger launch water depth,the bigger pressure magnitude of tail bubble and the shorter pressure oscillation period.

underwater vehicle;tail bubble;dynamic mesh;transport velocity;launch water depth

131.3+2

A

10.3969/j.issn.1007-7294.2014.07.001

1007-7294（2014）07-0739-07