天然裂缝性油藏渗吸规律
2014-06-15孟庆帮刘慧卿王敬
孟庆帮,刘慧卿,王敬
(中国石油大学石油工程学院教育部重点实验室,北京102249)
0 引言
世界上大约有一半的油藏为碳酸盐岩油藏,大多都是天然裂缝性油藏[1-2]。相对于裂缝来说,由于基质渗透率比较小,注入水很容易沿着裂缝通道窜流,导致基质的波及范围很小[3-4]。由毛细管压力引起的自发渗吸现象是裂缝性油藏中的一种重要渗流现象,在水湿性油藏中,原油会因自发渗吸现象由基质向裂缝流动。
认识油藏渗吸作用的影响因素,对于合理开发油藏、提高油藏采收率和经济效益有重要意义[5-7]。渗吸现象分为正向渗吸和反向渗吸2 种,但在天然裂缝性油藏中,特别是当基质被裂缝中的水环绕时,逆向渗吸通常是原油被采出的主要甚至是唯一的因素[8-10]。
为了研究裂缝性油藏的渗吸规律,国内外许多专家做了非常重要的工作。J.Bourblaux 等[11]使用天然岩心,研究了在不同饱和度和边界条件下正向和反向渗吸速度的大小,并应用数值方法对正向和反向渗吸的采收率进行了预测。A.Haugen 等[12]对裂缝性碳酸盐岩水驱实验和数值模拟方法进行了对比,并对基质毛细管压力和相渗曲线进行了敏感性分析。朱维耀等[13]通过核磁共振技术研究了孔隙度、渗透率、原油黏度和润湿性等对渗吸作用的影响。吴应川等[14]通过室内实验研究了渗吸速度与温度的关系。蔡喜东、王希刚等[15-16]对渗吸过程进行了数值模拟研究,并进行了敏感性分析。但多数学者只作了动态方面的研究,而且只是定性地讨论了渗吸作用的影响因素。
本文通过数值模拟方法,分别通过“静态”和“动态”2 种方法研究了各种因素对渗吸作用的影响,并且在静态情况下对不同影响因素进行公式拟合。
1 静态研究
使用Eclipse 数值模拟软件,建立概念地质模型,选用17×17×8 网格系统,X,Y 方向的步长均为100 m,Z 方向步长为10 m。油藏埋深为1 800 m,初始压力为18 MPa,油藏有效厚度为40 m,基质孔隙度为10%、渗透率为1×10-3μm2,裂缝孔隙度为1%、渗透率为1 000×10-3μm2,油藏温度为75 ℃,油藏条件下原油黏度为3 mPa·s。
为了研究基质原油的渗吸速度,笔者将裂缝中油相饱和度So设定为0,在基质中分别取不同的So值。经过数值模拟计算,20 d 内基质中So的变化很小,并且随着时间的变化呈现出较好的线性关系,所以笔者使用20 d 内基质中So的变化ΔSo来表征基质的瞬时渗吸速度。为了排除其他因素的影响,笔者在基质毛细管压力pc为0 时,计算基质中So的变化,结果显示其并未发生任何变化。
1.1 基质毛细管压力的影响
以饱和度中值压力来表征pc的大小。基质系统孔隙大小分布越集中,分选性越好,毛细管压力曲线的中间平缓段越长而且越接近水平线[17]。笔者采用理想化模型,将毛细管压力曲线中间平缓段设定为直线,用平缓段斜率kpc的绝对值表示孔隙的均匀程度,即kpc的绝对值越大,孔隙的分选性越差。
设定kpc1 表1 渗吸速度与影响参数拟合公式 从计算得到的pc与ΔSo的关系式可以看出:基质的渗吸速度随着pc的增大而增大,并且呈现出良好的线性关系;随着基质的So增高,直线的斜率也随之增大,即ΔSo随pc增大的速率加快。对于均匀孔隙结构,这是因为,So的增大致使油相相对渗透率增大,而对于非均匀孔隙结构,是由于油相相对渗透率和pc增加共同作用的结果。在孔隙均匀程度影响方面,当饱和度中值压力相同,So较大时,非均匀孔隙的pc较大,ΔSo也较大。 保持其他基础参数不变,只改变裂缝的渗透率,计算结果表明,裂缝渗透率对基质的渗吸速度影响非常小,因此,这里不再给出拟合公式。选取同样的毛细管压力曲线,裂缝渗透率取1 000×10-3μm2,改变基质渗透率Km,计算不同So条件下ΔSo与Km的关系,并拟合其关系式(见表1)。 由计算结果可以看出,基质中的ΔSo随Km的增大而增大,而且呈现出良好的线性关系。随着So的增大,直线的斜率同样随之增大,即基质中ΔSo增加的速率加快,这一点对于开采非均质油藏非常重要。由于在基质低渗区渗吸速度慢,所以应该由低渗向高渗区域注水,以提高基质中原油的采收率。 为了研究相渗曲线对基质中ΔSo的影响,应保持其他参数不变,通过改变相渗曲线端点值,分别计算ΔSo的变化。 可用Stone 修正模型归一化相渗关系式,通过计算得到相渗曲线[18]。计算结果表明,残余油饱和度Sorw下的水相相对渗透率对ΔSo的影响非常小,所以这里只对其他3 个参数进行拟合(见表1)。 拟合结果表明,ΔSo随着束缚水饱和度Swc的增大而增大,并呈现出良好的指数关系。这是因为Swc越大,在同一So条件下,油相相对渗透率Krocw也就越大,致使ΔSo较大;当Swc趋于0 时,ΔSo趋于一个定值,随着So的上升,ΔSo呈上升趋势;ΔSo随着Sorw的增加而减小,并呈现出良好的线性关系,So越小,直线斜率的绝对值越大,即在So较低时,Sorw对渗吸作用的影响更大;ΔSo与Krocw也呈现出良好的线性关系,并且直线的斜率随着So增高而增大。 为了研究原油黏度μ 对ΔSo的影响,应在其他参数保持不变的条件下,仅就μ 分别取值为1,3,5,10,50,100 mPa·s,计算基质的ΔSo,并拟合其与μ 的关系式(见表1)。 拟合结果表明,ΔSo随μ 的升高而下降,并呈现出良好的幂指数关系。所以,对于裂缝性稠油油藏来说,若采用常规水驱开采,基质中原油的采收率会很低。 在孔隙结构影响方面可以得到相似的结论,在注入孔隙体积倍数小时,随着孔隙结构非均匀程度的增强,ΔFOE 呈现增长趋势;在注入孔隙体积倍数大时,ΔFOE 增长趋势并不明显,甚至出现增幅下降趋势。这是因为,对于非均匀孔隙结构,在So较高时pc也较高,渗吸作用较强,但在后期,基质原油已经被大量采出,并且在So较低时非均质孔隙的pc较小,渗吸作用减弱,甚至消失。所以,对于油湿性油藏,较高的注入量可以在一定程度上提高油藏的采收率;对于水湿性油藏,特别是基质孔隙结构的非均匀程度很强,在油藏开发后期,pc较小时,较大注入量对提高采收率的效果并不明显。 动态研究同样采用静态研究中的概念地质模型,基础参数均保持不变。采用五点法井网,设置4 口注入井和9 口采油井,总的注入量与采出量之比为1∶1。分别计算在pc为0(油湿性油藏)和pc不为0(水湿性油藏)时不同注入孔隙体积倍数时的采出程度,并定义二者的差值为采出程度增量ΔFOE,以此表征在不同注入孔隙体积倍数时渗吸作用的影响。 图1为不同孔隙结构的基质在不同注入孔隙体积倍数时ΔFOE 与pc变化的关系。可以看出,随着pc上升,ΔFOE 呈现上升趋势,但其影响程度存在一个突变点。当pc小于突变点压力时,pc对ΔFOE 影响较大,而在突变点之后,影响较小。这表明,在动态假设中,基质的ΔSo和静态中不同,它并不随着pc的上升而呈直线上升趋势,而是在pc高时增速放缓。所以,水湿性油藏较油湿性油藏在同样的注入孔隙体积倍数时,其采出程度会有较大幅度的提高,但强水湿性油藏较弱水湿性油藏采出程度的提高幅度并不大。 由图1还可以看出,在注入孔隙体积倍数小时,ΔFOE 随着注入孔隙体积倍数的增大而增大,但在注入孔隙体积倍数大时,ΔFOE 增加幅度较小,甚至在pc低时其增幅有下降现象。这是因为,在注入孔隙体积倍数小时,基质中的So较高,渗吸作用较为明显,ΔFOE较大;在注入孔隙体积倍数大时,水湿性油藏基质中的So下降幅度较大,渗吸作用减弱,甚至消失,此时油湿性油藏基质中的So依旧较高。由于裂缝与基质之间存在压差,水驱作用仍旧可以采出一部分原油,所以,此时ΔFOE 增长放缓,甚至出现增幅下降的现象(见图1b,1c)。 图1 ΔFOE-pc 关系 图2为不同注入孔隙体积倍数时ΔFOE 与Km变化的关系。可以看出,Km对ΔFOE 的影响存在1 个明显的拐点。在注入孔隙体积倍数小且当Km低于拐点渗透率时,采出程度增量呈上升趋势,Km高于拐点渗透率时,采出程度增量并没有明显变化。这是因为:在Km较低时,油湿性油藏基质原油很难被采出,而水湿性油藏由于存在渗吸作用其采出程度较高,并且Km越大,渗吸作用采出的基质原油越多,所以ΔFOE 呈现上升趋势;在Km较高时,油湿性油藏部分基质原油可以由水驱作用采出,并且随着Km的增大其采出程度增大,此时渗吸作用也会随着Km的增大而增强,但水湿性油藏中渗吸作用的增油量与油湿性油藏中的增油量相互抵消,所以ΔFOE 变化很小。 图2 ΔFOE-Km 关系 笔者同时绘出了采出程度和注入孔隙体积倍数的关系曲线。当注入孔隙体积倍数小且Km较小时,油湿性油藏采出程度随Km的变化非常小,而在Km较大时,油湿性油藏采出程度出现较大变化,这与上述解释相吻合。 在注入孔隙体积倍数大时,Km高于拐点渗透率,ΔFOE 出现下降现象。这是因为,当注入孔隙体积倍数大且Km较大时,水湿性油藏基质中的So较低,渗吸作用减弱甚至消失,而油湿性油藏由于基质中的So较高,水驱作用仍然可以采出部分原油,致使采ΔFOE 下降。所以,对于油湿性油藏,特别是Km较高时,较大的注入孔隙体积倍数可以在一定程度上提高采收率;对于水湿性油藏,在Km较低时,较大的注入孔隙体积倍数可以较大幅度地提高采收率,而Km较高时,较大的注入孔隙体积倍数对采收率的提高程度有限。 图3为不同注入孔隙体积数时ΔFOE 与相对渗透率曲线端点变化的关系。由图3a可以看出,在注入孔隙体积倍数小时,ΔFOE 随Swc的变化并不明显,但在注入孔隙体积倍数大时却呈下降趋势,这似乎与静态中得到的规律并不吻合。这是因为,Swc越大,基质的初始含油饱和度越低,由静态关系式计算可以得出,随着Swc的上升,初始含油饱和度下降,基质的ΔSo呈现下降趋势。为了更加有效地表示这种下降趋势,笔者绘出了Swc和原油累计产量增值的关系曲线。结果显示,无论注入孔隙体积倍数小还是大,原油产量均呈现出明显的下降趋势。 图3 ΔFOE 与相渗曲线端点的关系 在残余油饱和度Sorw影响方面,Sorw越高,基质中ΔSo变化越慢,ΔFOE 也就越小(见图3b)。在注入孔隙体积倍数小时,ΔFOE 下降速度较慢,在注入孔隙体积倍数大时,其下降速度较快。这是因为,在注入孔隙体积倍数小时,基质中的So较高,Sorw对渗吸作用的影响并不明显,但在注入孔隙体积倍数大时,基质中的So较低,Sorw对渗吸作用的影响增强,导致ΔFOE 下降速度加快,这与静态中得出的结论相吻合。 在Krocw影响方面,当相对渗透率低于0.2 时,ΔFOE 上升幅度较大,而在相对渗透率大于0.2 时,ΔFOE 的变化与pc影响相似,即变化很小,甚至出现下降现象(见图3c)。所以,Krocw对渗吸作用的影响同样存在一个拐点。 图4为ΔFOE 与μ 变化的关系。可以看出,在注入孔隙体积倍数小时,基质中的So依旧较高,ΔSo也较大。由于μ 越大,渗吸作用越弱,所以导致ΔFOE 下降。由0.3 PV 的曲线可以看出,在μ 较低时,ΔFOE 下降较快,在μ 很高(超过15 mPa·s)时,其变化并不明显,与静态中幂指数关系相吻合。 图4 ΔFOE-μ 关系 当注入孔隙体积倍数大且μ 较低时,ΔFOE 随μ的变化并不明显,但在μ 较高时,ΔFOE 随着μ 的增大而降低。这似乎与静态中ΔSo与μ 之间的幂指数关系并不吻合。这是因为,在μ 较低时,较大的注入孔隙体积倍数使水湿性油藏基质原油被大量采出,渗吸作用减弱甚至消失,而油湿性油藏由于基质中的So较高,水驱作用仍可以驱出基质中的部分原油,导致ΔFOE变化并不明显。但在μ 高时,水湿性油藏基质中的So依旧较高,渗吸作用比较明显,ΔFOE 呈现出下降趋势。所以,对于μ 较低的油湿性油藏,较大的注入孔隙体积倍数可以较大幅度地提高采收率,而对于μ 较高的水湿性油藏,较大的注入孔隙体积倍数也可以较大幅度地提高采收率。 1)静态下,ΔSo与pc,Km,Sorw和Krocw均呈线性关系,与Swc呈指数关系,与μ 呈幂指数关系。在pc,Km,Swc条件下,Krocw越大,ΔSo越大;Sorw越大,ΔSo越小。 2)对于Km较高、μ 较低的油湿性油藏,较大的注入孔隙体积倍数可以较大程度地提高采收率;对于Km较低、μ 较高的水湿性油藏,较大的注入孔隙体积倍数也可以较大程度地提高采收率。 3)渗吸作用的影响主要在注入孔隙体积倍数较小而不是太小阶段,即裂缝中水相饱和度较高而基质中的So较高的阶段。 [1]陈欢庆,胡永乐,赵应成,等.火山岩储层地质研究进展[J].断块油气田,2012,19(1):75-79. [2]李勇,李保柱,胡永乐.碳酸盐岩油气藏数值模拟研究综述[J].石油地质与工程,2009,23(1):75-78. [3]张立强,孙雷,陈丽群,等.裂缝性油藏井网水驱油物理模拟研究[J].断块油气田,2013,20(3):341-345. [4]陈莹莹,孙雷,田同辉,等.裂缝性碳酸盐岩油藏可视化模型水驱油实验[J].断块油气田,2012,19(1):92-94. [5]计秉玉,陈剑,周锡生,等.裂缝性低渗透油层渗吸作用的数学模型[J].清华大学学报:自然科学版,2002,42(6):711-713. [6]Akin S,Kovscek A R.Imbibition studies of low-permeability porous media[R].SPE 54590,1999. [7]李士奎,刘卫东,张海琴,等.低渗透油藏自发渗吸驱油实验研究[J].石油学报,2007,28(2):109-112. [8]Yu L,Evje S,Kleppe H,et al.Spontaneous imbibition of seawater into preferentially oil-wet chalk cores-experiments and simulations [J].Journal of Petroleum Science and Engineering,2009,66(3):171-179. [9]李爱芬,凡田友,赵琳.裂缝性油藏低渗透岩心自发渗吸实验研究[J].油气地质与采收率,2011,18(5):67-73. [10]姚同玉,李继山,王建,等.裂缝性低渗透油藏的渗吸机理及有利条件[J].吉林大学学报:工学版,2009,39(4):937-940. [11]Bourbiaux J,Kalaydjian F.Experimental study of cocurrent and countercurrent flows in natural porous media[J].SPE Reservoir Engineering,1990,5(3):361-368. [12]Haugen A,Ferno M,Graue A.Comparison of numerical simulations and laboratory waterfloods in fractured carbonates [R].SPE 110368,2007. [13]朱维耀,鞠岩,赵明,等.低渗透裂缝性砂岩油藏多孔介质渗吸机理研究[J].石油学报,2002,23(6):56-59. [14]吴应川,张惠芳,代华.利用渗吸法提高低渗油藏采收率技术[J].断块油气田,2009,16(2):80-82. [15]蔡喜东,姚约东,刘同敬,等.低渗透裂缝性油藏渗吸过程影响因素研究[J].中国科技论文在线,2009,4(11):806-812. [16]王希刚,宋学峰,姜宝益,等.低渗透裂缝性油藏渗吸数值模拟研究[J].科学技术与工程,2013,13(7):246-250. [17]胡勇,于兴河,陈恭洋,等.平均毛管压力函数分类及其在流体饱和度计算中的应用[J].石油勘探与开发,2012,39(6):733-738. [18]Stone H L.Probability model for estimating three-phase relative permeability[J].Journal of Petroleum Technology,1970,22(2):214-218.
1.2 裂缝和基质渗透率的影响
1.3 相对渗透率曲线的影响
1.4 原油黏度的影响
2 动态研究
2.1 毛细管压力的影响
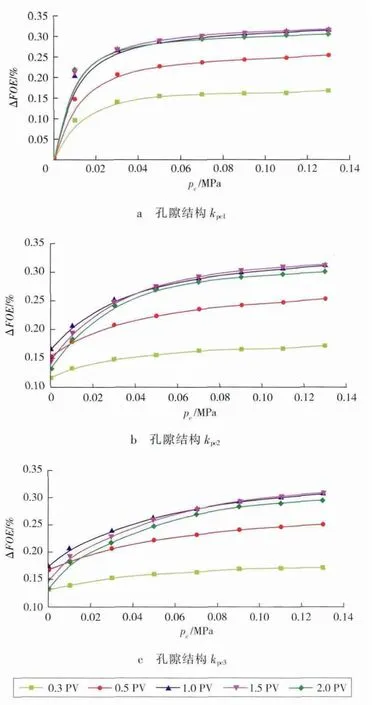
2.2 基质渗透率的影响
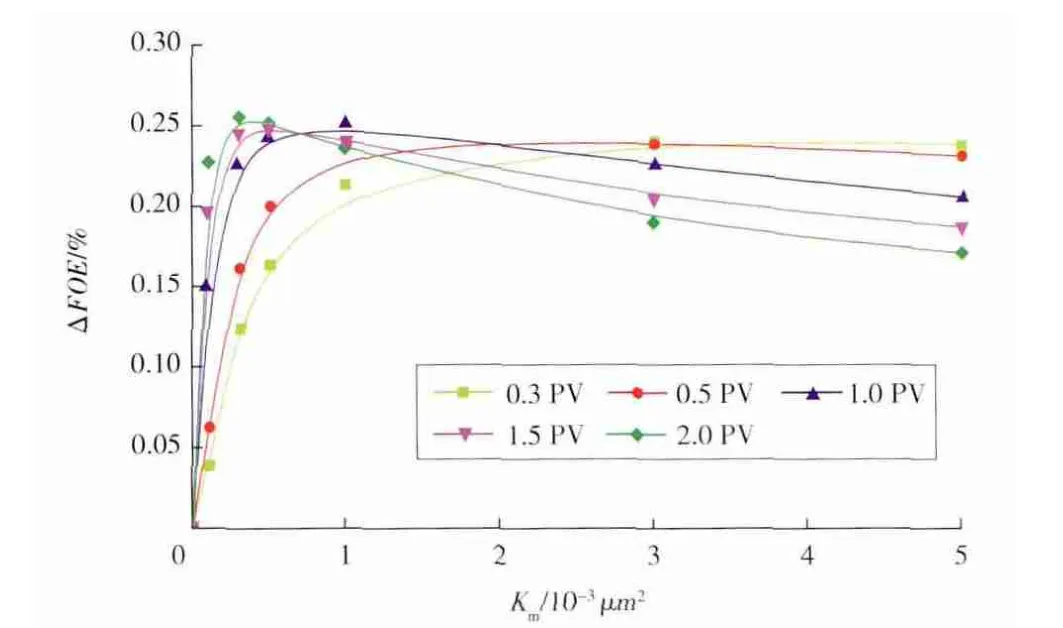
2.3 相渗曲线的影响

2.4 原油黏度的影响

3 结论
