桥梁断面气动导数识别的模态参数插值方法研究①

董双虎

(同济大学桥梁工程系，上海 200092)

0 引言

气动导数是描述桥梁结构气动性能的重要参数，对桥梁颤抖振分析都必不可少.目前，气动导数的识别有自由振动法，强迫振动法和CFD方法，其中自由振动法因试验装置简单，应用较多.

1971年，Scanlan等人提出了最早的气动导数识别的节段模型自由振动方法[1]，该方法分状态识别气动导数，工作量大且识别精度不高.1984年，谢霁明发展了基于Karman滤波器的初脉冲耦合振动法[2]，方法中采用了非定常自激力模型，通过比较非定常自激力模型和Scanlan自激力模型建立自激力系数矩阵和Scanlan气动导数之间的关系求得气动导数.1994年，Sarkar提出了气动导数识别的MITD法[3]，通过迭代来减小参数识别精度，但未能解决时延参数选取的问题.二十世纪九十年代，日本学者Yamada和Iwamoto也先后在桥梁气动导数的识别中应用了耦合自由振动方法[4～5].1998 年，张若雪提出了桥梁断面气动导数识别的总体最小二乘法[6]，该方法用交叉迭代进行总体最小二乘拟合.2001年，丁泉顺针对总体最小二乘法的不足提出了修正总体最小二乘法[7]，提高了高折减风速下气动导数识别的稳定性.

上述气动导数识别的自由振动法均采用了传统处理方法[8]，即计算与竖弯有关的气动导数时采用频率w1，计算与扭转有关的气动导数时采用频率w2.为克服该传统气动导数识别方法中的缺陷，丁泉顺提出了一种模态参数插值求气动导数的方法并给出了数值验证[9].在此基础上，本文主要探讨了一种由归一化提取可直接插值的模态参数的方法，数值算例验证表明该方法是可行的，从而保证了模态参数插值求气动导数的可行性.

先介绍气动导数识别的模态参数插值方法.

1 气动导数识别的模态参数插值方法

考虑自激力作用的两自由度桥梁节段模型的运动方程为:

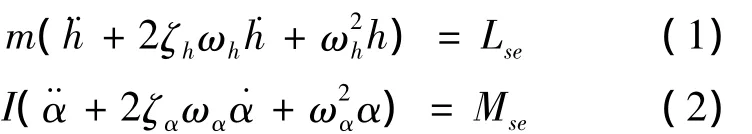
其中h为竖向位移，α为扭转角，m为单位长质量，I为单位长质量惯矩，Lse和Mse是气动升力和升力矩.

根据Scanlan的颤振理论，升力和升力矩可写成如下形式:

其中U为风速，B为模型宽度，ρ为空气密度，折减频率K=ωB/U(i=1，2，3，4)是气动导数.

将(3)(4)式代入(1)(2)中，移项并令

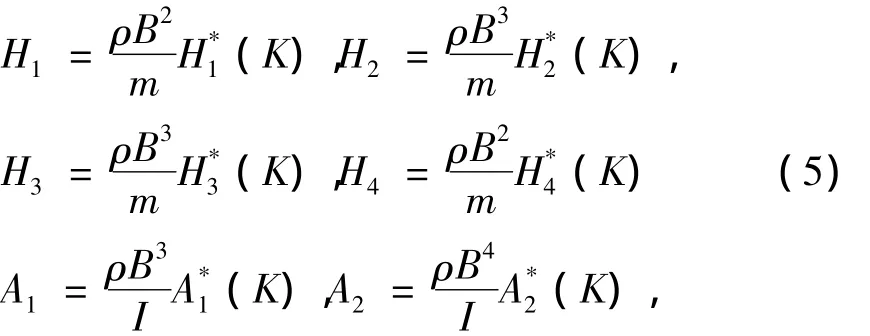
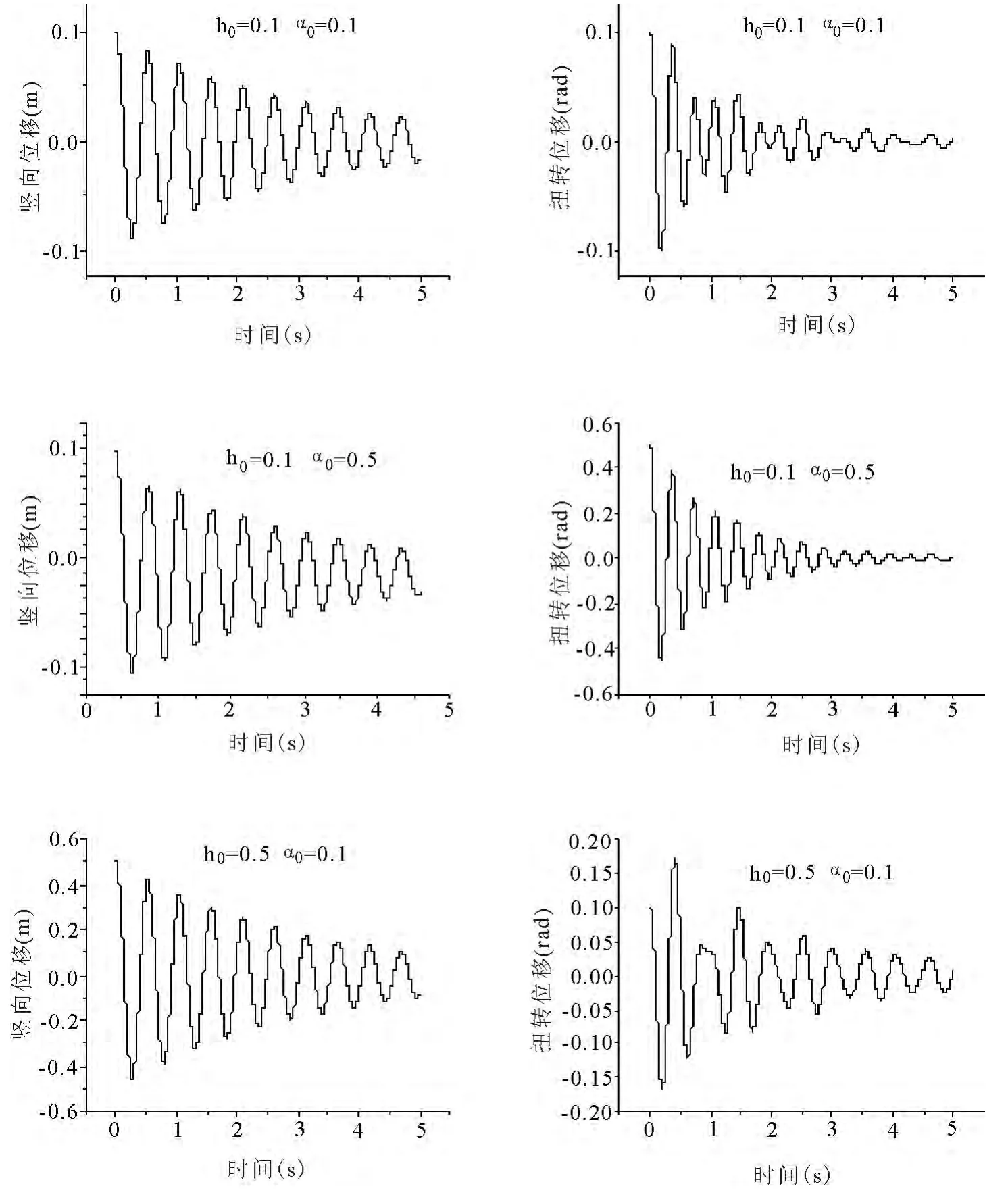
图1 不同初始激励下桥梁断面的位移响应时程

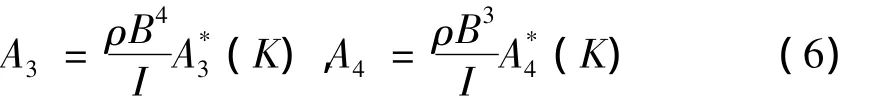
则方程(1)(2)变为

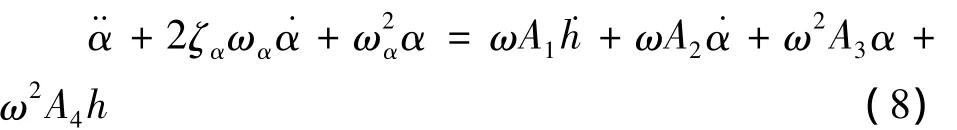
取x(t)=[h(t)α(t)]T，则方程(7)(8)可写为

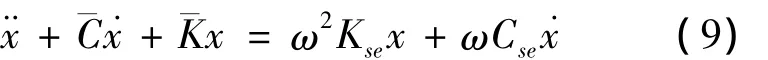
式中

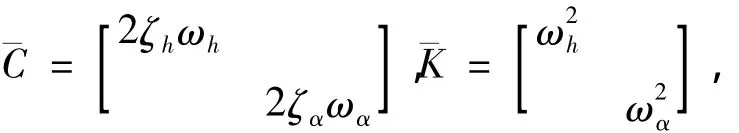
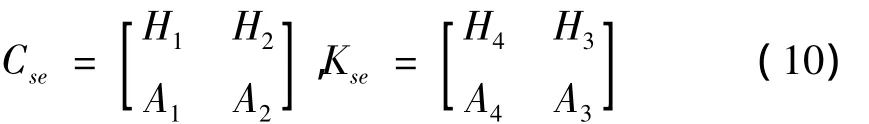
设方程的解为x(t)=Ψeλt，其中λ和Ψ依次为系统(包括结构和自激力)的复特征值和复特征向量，且λ=(－ζ+i)ω=(ζ为复模态的阻尼比，ω为圆频率)，由此可得出上述控制方程的特征方程为

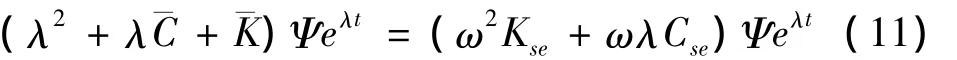
已知同一折减风速下的八个气动导数，对式(11)进行系统的复特征分析可以得到该折减风速下的一组模态参数，反之，由同一折减风速下的一组模态参数可求得该折减风速下的八个气动导数.为了确定包含气动导数的系统自激力矩阵，式(11)可进一步写成

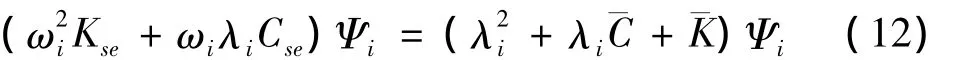
也即

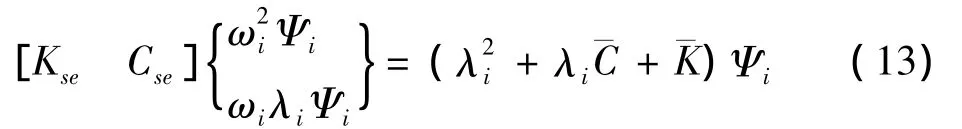
每一个i值对应两组共轭的复特征值和复特征向量，八个方程可求得八个气动导数.因此，气动导数的求解转化为同一折减风速下的模态参数的识别.

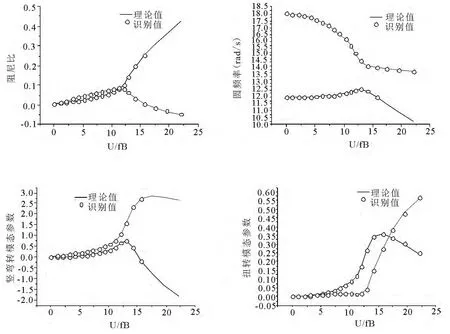
图2 桥梁断面系统振动模态参数识别值与理论值的比较

2 模态参数提取方法

系统的自由振动响应在物理坐标系中可表示为

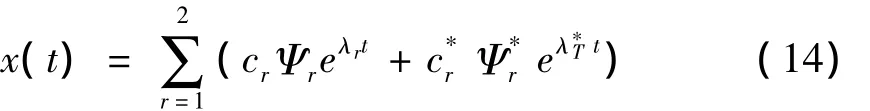
其中 cr，为由初始条件决定的常数，且成共轭对的形式出现.令λr= αr+βir，λ*r= αr－ iβr，代入上式可得

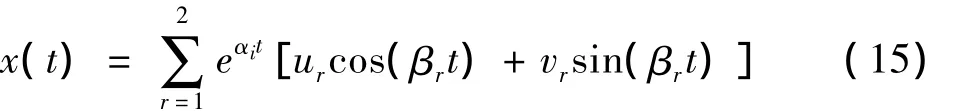
这里采用总体最小二乘法获取低试验风速下系统模态参数[6]，而高试验风速下系统模态参数采用传统最小二乘法按单一模态拟合，由于模态振型参数和初始激励有关，建议一种归一化方法提取与初始激励无关并可直接插值的模态参数，较式

(14)和(15)不难得出如下对应关系

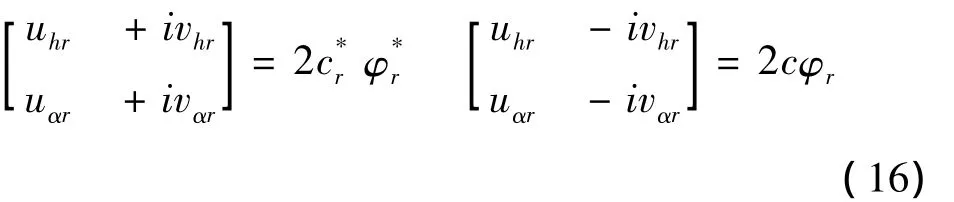
式中，r=1，2分别对应竖弯模态和扭转模态.

由式(16)可知，只要确定模态中某种运动的幅值和相位，则另一种运动的幅值和相位也相应确定，可直接插值的模态参数也即相应确定.以扭转模态为例

不妨令uα2－iv2α=1，则可按如下方法提取可直接插值的模态参数.

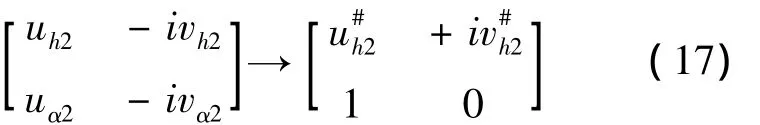
不难证明，变换后的参数与初始激励无关.同理可提取可直接插值的竖弯模态参数.对不同风速下的模态参数进行线性插值，即可得到同一折减风速(或折减频率)下的一组模态参数，进而由式(13)可求得气动导数.

图3 桥梁断面气动导数识别值与理论值的比较

3 算例分析

方便起见，本文采用一组特殊形式的气动导数获得响应时程对上述方法进行验证.

取两自由度桥梁节段模型断面宽B=0.5m，单位长度质量m=10kg/m，单位长度质量惯矩Im=0.2kg·m2/m，空气密度 ρ=1.225kg/m3，竖弯和扭转固有频率依次为 12.0rad/s，18.0rad/s.阻尼比均取为0.005.气动导数表达为

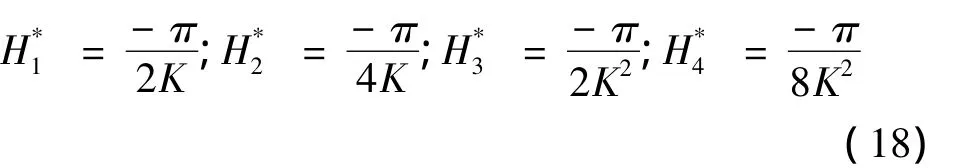
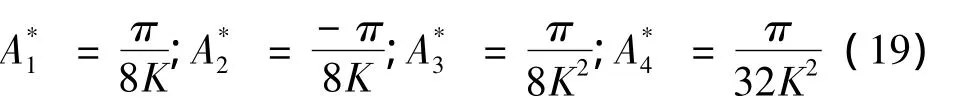
风速从零开始每级增加1m/s直至18m/s.用matlab进行系统非线性时域分析求得结构的动力响应时程.给系统不同的初始激励，可以得到不同激励下平板振动的位移响应时程.本文以三组5m/s时程为例，验证归一化提取可直接插值的模态参数的可行性.

用总体最小二乘法获取上述三组不同激励下桥梁断面板的阻尼，频率，幅值等识别参数并归一化处理得到模态参数.以竖弯模态为例，表1为计算结果.(注:h0，a0为初始激励竖弯位移和扭转角).

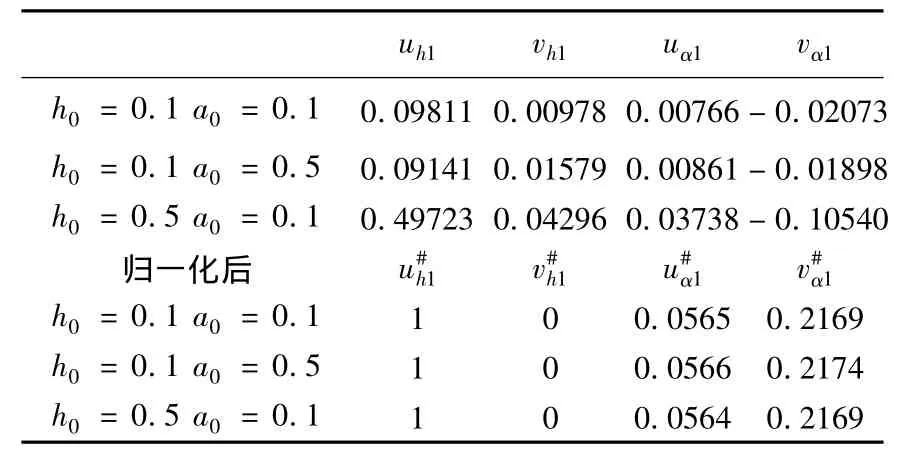
表1 不同初始激励下模态参数提取结果

由表1可知，不同初始激励下得到的可直接插值的模态参数是和初始激励无关的常数，即验证了归一化提取可直接插值的模态参数方法的可行性.

为了进一步验证上述模态参数提取的归一化方法，本文进行了两自由度系统的模态参数和气动导数的识别.时程信号由上述三种不同的初始激励通过时域分析得到.图2给出了各风速下系统振动模态参数的识别结果，其中实线为理论值，圆点为识别值，两者高度吻合.图3给出了各气动导数的识别结果，其中实线为理论值，圆点为识别值，除了H2*个别点由于插值误差稍有偏差外，气动导数识别值均与理论值吻合较好，从而表明上述识别参数

归一化处理提取模态参数的方法是可行的.

4 结语

由系统复模态的特征分析发现，同一折减风速(或折减频率)下的模态参数和该折减风速(或折减频率)下的气动导数是一一对应的.基于该思想可建立系统振动模态参数确定桥梁断面气动导数的方法.该方法的关键是获取同一折减风速(或折减频率)下的模态参数.在此基础上，本文主要探讨了一种归一化提取可直接插值的模态参数的方法.数值算例验证发现，模态参数识别结果和理论值完全吻合，在此基础上用插值模态参数求得的气动导数也与理论值吻合较好，从而验证了该方法的可靠性和适用性.

[1]Scanlan R H.et al.Airfoil and Bridges Deck Flutter Derivatives[J].EM6，1971，ASCE:1717－1733.

[2]谢霁明.识别非定常气动力模型的初脉冲耦合振动法[J].空气动力学学报，4(3)，1986年第9期.

[3]Sarker P.P.et al.Identification of Aeroelastic Parameters of Flexible Bridges[J].EM8，1994，ASCE:1718－1741.

[4]Yamada H.，Miyata T.，Ichikawa H.Measurement of Aerodynamic Coefficients by System Identification Methods[J].Journal of Wind Engrg.and Industrial Aerody.，Vol 41－ 44，1992:1255－1263.

[5]Iwanmoto M.，Fujino Y.Identification of Flutter Derivatives of Bridge Deck from Free Vibration Data[J].Journal of Wind Engrg.and Industrial Aerody.，Vol 44－45，1995:55－63.

[6]张若雪.桥梁结构气动导数识别的理论和试验研究[D].上海:同济大学，1998.

[7]丁泉顺，陈艾荣，项海帆.桥梁断面气动导数识别的修正最小二乘法[J].同济大学学报，2001，(1).

[8]项海帆，等.《现代桥梁抗风理论与实践》[M].北京:人民交通出版社，2005.

[9]丁泉顺，王景，朱乐东.桥梁断面颤振导数识别的耦合自由振动方法[J].振动与冲击，2012，(24).