大跨度单层混合型球面网壳非线性稳定性研究
2014-06-12郭远翔黄慧隆
郭远翔黄慧隆
(1.华南理工大学土木与交通学院,广州510641;2.华南理工大学建筑设计研究院,广州510641)
大跨度单层混合型球面网壳非线性稳定性研究
郭远翔1,2黄慧隆1,*
(1.华南理工大学土木与交通学院,广州510641;2.华南理工大学建筑设计研究院,广州510641)
本文采用大型通用有限元软件ANSYS对大跨度单层混合型球面网壳弹塑性稳定性进行研究,分析了初始缺陷、荷载不对称分布、支承条件及非线性对网壳稳定性的影响,并研究了初始缺陷对网壳动力稳定性的影响情况。
大跨度单层混合型球面网壳,非线性,稳定性,ANSYS
1 网壳有限元分析
1.1 概 况
目前对于单层球面网壳的最大跨度,《网壳结构技术规程》(JGJ 61—2003)[1](以下简称《规程》)建议不宜大于60 m。但随着经济的发展及建筑美观的需要,大跨度的单层球面网壳也有不少工程实例,如日本名古屋体育馆,其跨度就达到187 m。对于大跨度单层球面网壳而言,影响其承载力的主要因素是结构的稳定性[2-4],因此有必要对大跨度单层球面网壳结构的稳定性进行分析研究。
1.2 分析模型
1.2.1 结构几何尺寸
由于国内对于单一形式的单层网壳的稳定性问题研究比较多,却比较少涉及大跨度单层混合型网壳的稳定性研究,因此本文采用的分析模型为K8-联方混合型单层网壳,如图1所示。其跨度达84 m,矢高16.8 m,矢跨比为0.2,其中主杆和纬杆采用φ158 mm×6 mm,而斜杆则采用φ152 mm×6 mm。网壳仅在节点上承受竖向均布荷载,周边节点考虑了铰接和固接两种支承条件。本文在进行网壳稳定性分析时,同时考虑材料非线性与几何非线性。

图1 分析模型Fig.1 The analysismodel
1.2.2 材料参数及单元选取
钢材选用Q345,屈服强度为310 MPa,弹性模量取为2.06×105MPa,泊松比取为0.3,密度为7 800 kg/m3。考虑钢材屈服后的强化,采用双折线模型,强化模量为2.06×103MPa。整个模型均采用Beam188单元,每根杆件划分5段。
1.3 有限元分析结果
1.3.1 初始缺陷对网壳稳定性的影响
对于单层球面网壳,研究表明其对初始缺陷高度敏感,[5]但实际工程中初始缺陷是难以避免的。图2是本文用于分析的K8-联方混合型单层球面网壳考虑16种不同大小的初始缺陷时所绘制的荷载—位移全过程曲线,图3是网壳极限荷载随缺陷值的变化情况。
由图2可以看到,单层球面网壳由于受到材料非线性的影响,在局部失稳后由于塑性变形的发展而使整体刚度迅速下降,因此在经过临界点后网壳始终没有达到反向稳定位置,荷载不断下降[6]。另外,随着缺陷值的增加,在到达极限荷载前曲线的斜率也在不断地下降,说明结构的整体刚度由于初始缺陷的存在而降低。
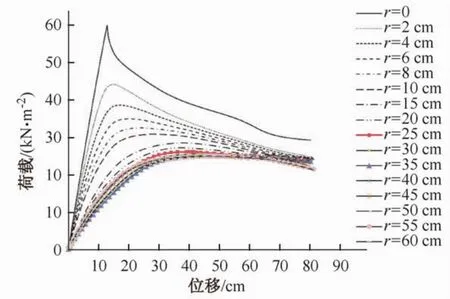
图2 不同初始缺陷值对应的全过程曲线Fig.2 The complete loading-displacement curves of different initial imperfections
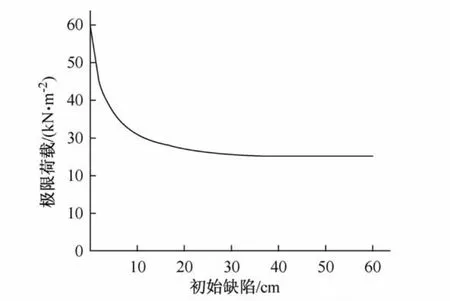
图3 极限荷载随初始缺陷值变化曲线Fig.3 The relative curve between the limit loads and the initial imperfections
从图2和图3可以看出,K8-联方混合型单层网壳对于初始缺陷非常敏感,尤其当初始缺陷较小时。随着初始缺陷值的增加,极限荷载值的下降速度逐渐减慢,最终稳定在25 kN/m2左右。因此实际工程中应尽可能的减少产生初始缺陷。
表1是网壳的极限荷载随着缺陷值增加时的下降率。由表中数值可以看到,仅仅是2 cm的缺陷值即造成极限荷载相对完整网壳降低了26.3%,而达到《规程》[1]建议的最大计算值L/300,即28 cm时,网壳的极限荷载下降了57%,即降低超过一半。当缺陷值达到40 cm(L/210)时,极限荷载下降率达到最大值并最终稳定在58%左右。
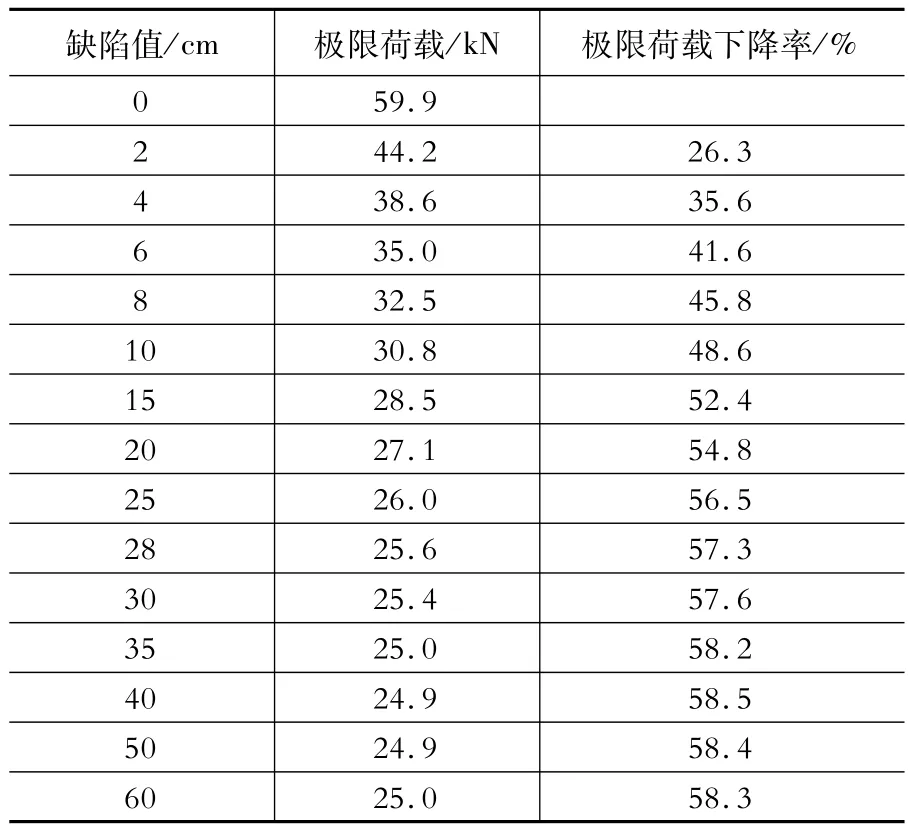
表1 网壳极限荷载随初始缺陷值增加时的下降率Table 1 The lim it load decrease rate due to the increase of initial imperfections
由上述分析可知,对于大跨度单层K8-联方混合型网壳来说,可以将L/210的安装偏差定为用于设计和分析的最大初始缺陷值,并把理想网壳极限荷载的42%作为实际网壳的极限承载力。
1.3.2 荷载不对称分布对网壳稳定性的影响
《规程》指出,在球面网壳的全过程分析中,可以按满跨均布荷载进行[1],而国内的研究也表明荷载不对称分布对网壳稳定性的影响并不明显[6],但考虑到本文算例跨度已大于规程中建议的60 m,且为K8-联方混合型网壳,因此有必要考虑荷载不对称造成的影响。图4是对网壳分别按4种不同荷载比例(q/g=0,0.25,0.5,0.75)的不对称荷载布置进行的全过程分析得到的曲线,其中,g为恒载,采用全跨布置;q为活载,采用半跨布置。
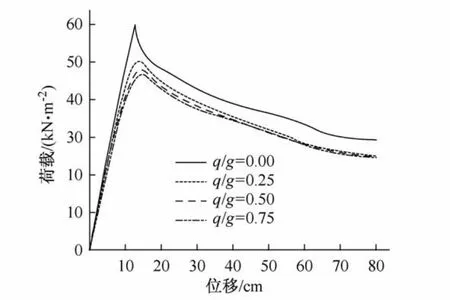
图4 不同荷载比例对应的全过程曲线Fig.4 The complete loading-displacement curves of different load ratios
从图4可以看出,考虑荷载不对称布置时的极限荷载相对于不考虑荷载不对称布置时的极限荷载降低比较明显,但不如考虑初始缺陷时造成的影响大,而增加荷载比例,即增加活荷载的大小对极限荷载的影响则比较小。因此,在实际工程中建议对跨度比较大且为混合型的球面网壳补充考虑半跨活荷载布置造成的影响。
1.3.3 支承条件对网壳稳定性的影响
《规程》[1]并没有明确指出单层网壳在分析时的支承条件,因此对于本文采用的大跨度K8-联方混合型网壳是有必要考虑铰接支承与固接支承带来的影响的。图5是考虑铰接及固接支承条件时对完整网壳(r=0)及带有8 cm初始缺陷(r=8 cm)网壳的极限荷载的影响情况。
从图中可以看出,固接与铰接时的全过程曲线变化规律都非常接近,考虑初始缺陷的情况下两曲线几乎完全重合。无论是完整网壳还是带缺陷的网壳,支承条件对其的影响都非常小,可以忽略不计,因此在实际工程中对于大跨度的单层K8-混合型网壳可以选择铰接或者固接进行分析。
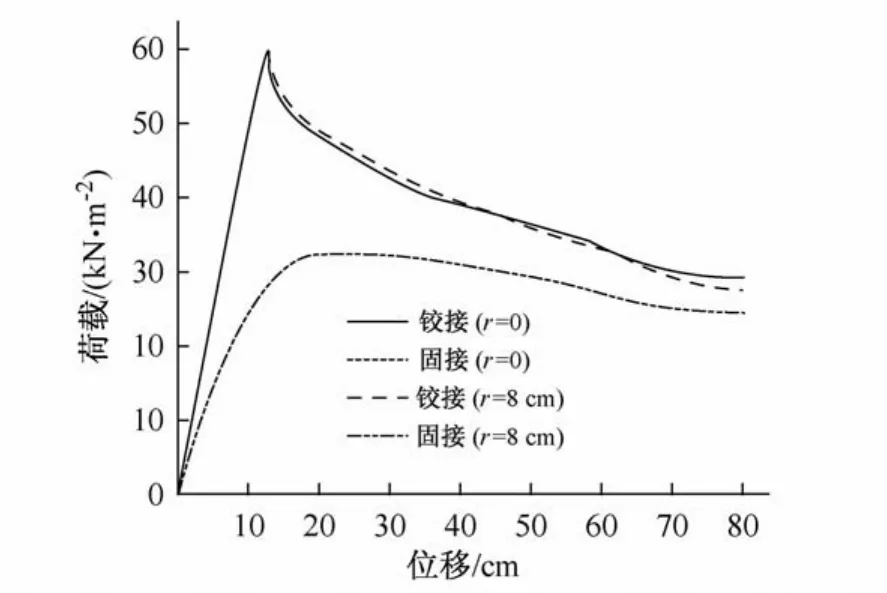
图5 不同支承条件对应的全过程曲线Fig.5 The complete loading-displacement curves under different support conditions
1.3.4 非线性对网壳稳定性的影响
《规程》[1]规定在进行网壳结构的稳定性计算时应考虑结构几何非线性的影响。对于本文的大跨度空间网壳来说,分析非线性带来的影响是很有必要的。本文分别绘制了只考虑材料非线性、只考虑几何非线性以及同时考虑双非线性时的荷载—位移全过程曲线,如图6所示。
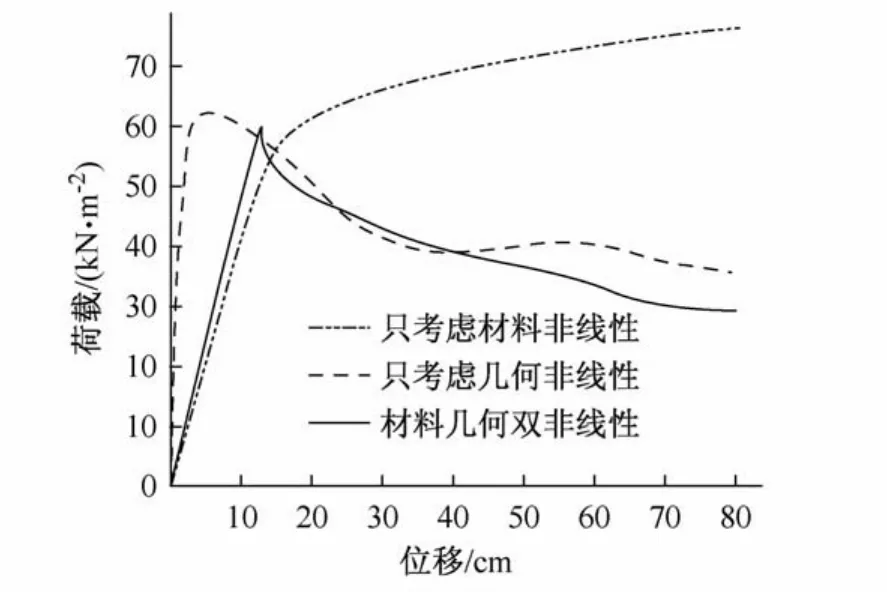
图6 考虑不同非线性情况对应的全过程曲线Fig.6 The complete loading-displacement curves under different nonlinear situations
从图中可以看出,当只考虑材料非线性时,网壳没有出现极值点失稳,而是分支点失稳,荷载在经过分支点后没有出现下降,而是一路走高,其失稳前的整体结构刚度及失稳时的竖向位移与考虑双非线性时的情况差别不大。若只考虑几何非线性,网壳则出现极值点失稳,荷载—位移全过程曲线在经过极值点后开始下降,并在随后出现第二次失稳,但对于实际工程已无意义。另外,其失稳前结构整体刚度要远大于考虑双非线性的情况,而发生失稳时的竖向位移则小于考虑双非线性的情况。三种情况的极限失稳荷载值相差不大,但由于非线性对于结构整体刚度及失稳形式的影响比较大,实际工程中对于大跨度的K8-联方型网壳结构的分析设计应同时考虑材料非线性及几何非线性。
1.3.5 非线性与初始缺陷对网壳破坏形态的影响
非线性及初始缺陷的存在不仅会影响荷载—位移全过程曲线的形状,还有可能会改变网壳的破坏形态。本文认为当网壳达到极限荷载时为破坏,给出了只考虑材料非线性、只考虑几何非线性、考虑双非线性及考虑双非线性并分别并带有28 cm(L/300)和40 cm(L/210)初始缺陷时的网壳结构破坏形态,如图7-图11所示。
由图中可以看出,只考虑材料非线性与考虑双非线性时的破坏形态比较接近,均表现为中间起算第二环处出现下凹,而只考虑几何非线性时的网壳破坏形态则表现为在支承环起算第二环与第三环处出现凹陷。另外,带28 cm(L/300)初始缺陷和带40 cm(L/210)初始缺陷并考虑双非线性的网壳破坏形态均表现为中部K8型网壳出现三处局部失稳。
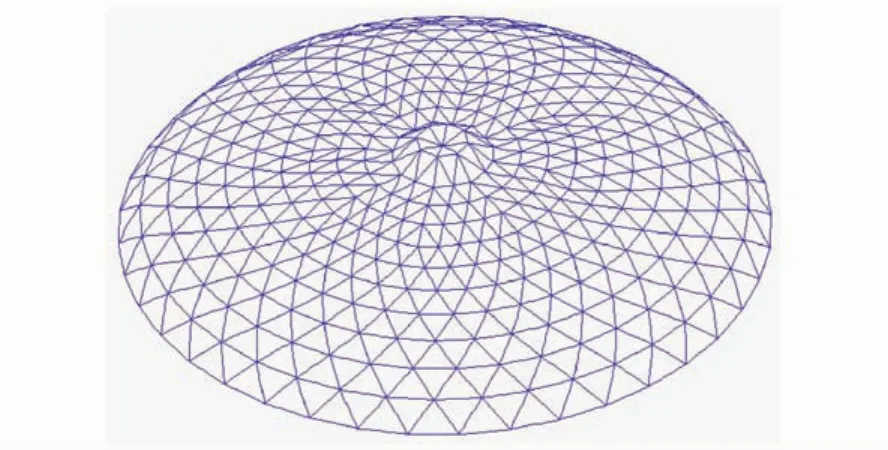
图7 只考虑材料非线性时网壳的破坏形态Fig.7 The failuremode of reticulated shell with material nonlinearity
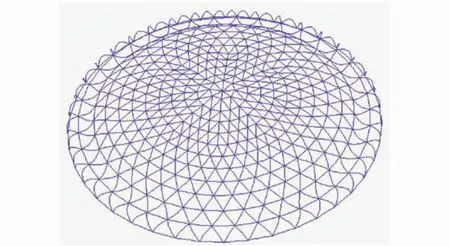
图8 只考虑几何非线性时网壳的破坏形态Fig.8 The failuremode of reticulated shellwith geometric nonlinearity
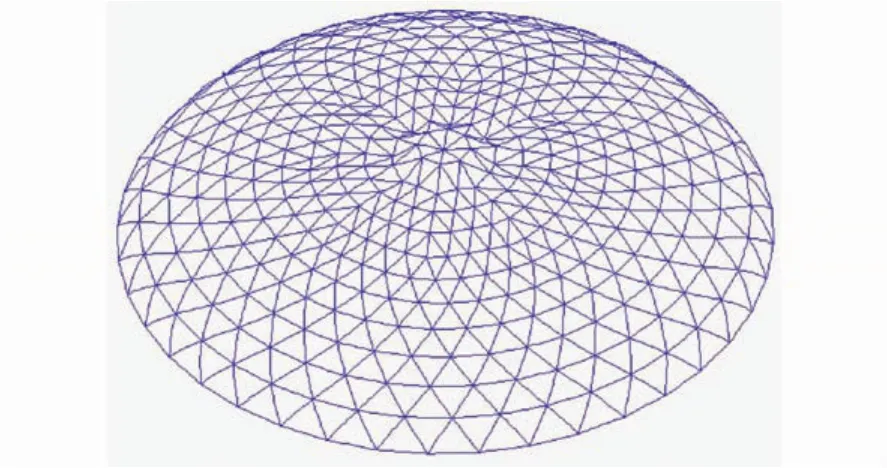
图9 考虑双非线性时网壳的破坏形态Fig.9 The failuremode of reticulated shell with double nonlinearity
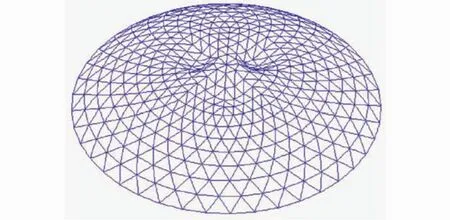
图10 考虑带28 cm初始缺陷及双非线性时网壳的破坏形态Fig.10 The failuremode of reticulated shell with 28 cm initial imperfection and double nonlinearity
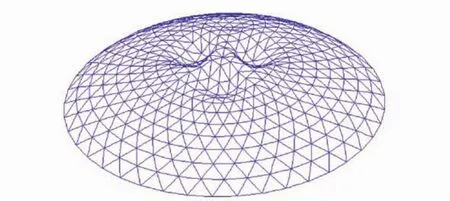
图11 考虑带40 cm初始缺陷及双非线性时网壳的破坏形态Fig.11 The failuremode of reticulated shell with 40 cm initial imperfection and double nonlinearity
由以上分析可知,初始缺陷对于网壳破坏形态的影响不容忽视,因此实际工程分析设计中应考虑初始缺陷的影响,并在施工中尽可能减小初始缺陷值。另外,非线性尤其是几何非线性的影响不容忽视,在实际工程设计分析中应尽可能考虑双非线性对网壳结构破坏形态的影响。
2 结 论
本文针对大跨度单层K8-联方混合型球面网壳的有限元研究主要得出以下结论和建议:
(1)大跨度单层K8-联方混合型球面网壳对于初始缺陷高度敏感,初始缺陷可使网壳承载力降低达58%,因此在实际设计中应考虑初始缺陷的影响,同时可以将理想网壳极限荷载的42%作为实际网壳的极限承载力,另外施工安装中应尽可能减小初始缺陷。
(2)荷载不对称布置对于K8-联方混合型网壳的极限荷载有一定影响,在实际工程中应适当考虑,但活载与恒载的比例变化对网壳极限荷载的影响则比较小,可以忽略。
(3)对于大跨度的单层K8-混合型球面网壳来说,无论是否具有初始缺陷,其边界支承条件的改变对其极限承载力的影响非常小,可以忽略不计。
(4)只考虑材料非线性和只考虑几何非线性两种情况虽然对网壳的极限荷载影响不大,但前者网壳将呈现分支点失稳。而后者将导致网壳在失稳前的整体刚度远大于考虑双非线性时的情况,因此实际工程中应尽可能考虑双非线性。
(5)非线性与初始缺陷对网壳结构破坏形态的影响不容忽视,因此实际工程中应充分考虑这两种情况,以防止对网壳结构的破坏形态判断不够准确。
[1] 中华人民共和国建设部.JGJ 61—2003网壳结构技术规程[S].北京:中国建筑工业出版社,2003.Ministry of Construction of the People's Republic of China.JGJ 61—2003 Technical specification for latticed shells[S].Beijing:China Architecture and Building Press,2003.(in Chinese)
[2] 孔丹丹,丁洁民.弦支网壳结构的静力分析[J].结构工程师,2006.22(4):5-28.Kong Dandan,Ding Jiemin.Static analysis of a suspended lattice shell structure[J].Structural Engineers,2006,22(4):5-28.(in Chinese)
[3] 车伟,李海旺,罗奇峰.单层椭圆抛物面网壳结构非线性整体稳定研究[J].郑州大学学报(工学版),2007,28(3):20-23.CheWei,LiHaiwang,Luo Qifeng.Study on nonlinear stability of single-layer elliptical paraboloid latticed shells[J].Journal of Zhengzhou University(Engineering Science Edition),2007,28(3):20-23.(in Chinese)
[4] 曹正罡,范峰,严佳川,等.基于ANSYS的大跨度单层球面网壳设计与分析[J].工程设计与计算机技术,2007,28(3):20-23.Cao Zhenggang,Fan Feng,Yan Jiachuan,etal.Struetural design and analysis of Long-span single-layer reticulated domes[J].Engineering Disign and Computer Technology,2007,28(3):20-23.(in Chinese)
[5] 李忠学.初始几何缺陷对网壳结构静、动力稳定性承载力的影响[J].土木工程学报,2002,35(1):11-14.Li Zhongxue.Effects of initial geometrical imperfections on dynamic stability of reticulated shell structures[J].China Civil Engineering Journal,2002,35(1):11-14.(in Chinese)
[6] 曹正罡,范峰,沈世钊.单层球面网壳的弹塑性稳定性[J].土木工程学报,2006,39(10):6-10.Cao Zhenggang,Fan Feng,Shen Shizhao.Elasto-plastic stability of single-layer reticulated domes[J].China Civil Engineering Journal,2006,39(10):6-10.(in Chinese)
Nonlinear Stability Analysis of a Large-span Single-layer M ixer Spherical Reticulated Shell Structure
GUO Yuanxiang1,2HUANG Huilong1,*
(1.School of Civil Engineering and Transportation,South China University of Technology,Guangzhou,510640,China;2.Architectural Design and Research Institute of South China University of Technology,Guangzhou,510640,China)
In this article,the universal finite element software ANSYS is used to analyse the nonlinear stability of a large-span single-layermixer spherical reticulated shell structure.The effects of initial imperfection,asymmetric load distribution,support conditions and the influences of geometrical nonlinearity and material nonlinearity to the stability behavior of this kind of reticulated shell structure are presented.In addition,the effects of initial imperfection to the dynamic stability is also discussed.
large-span single-layermixer spherical reticulated shell,nonlinear,stability,ANSYS
2013-04-18
*联系作者,Email:h.h.long@qq.com
