L1-L2正则化的图像复原交替优化算法

肖 宿，洪留荣，沈 克，郑 颖

淮北师范大学 计算机科学与技术学院，安徽 淮北 235000

L1-L2正则化的图像复原交替优化算法

肖 宿，洪留荣，沈 克，郑 颖

淮北师范大学 计算机科学与技术学院，安徽 淮北 235000

XIAO Su,HONG Liurong,SHEN Ke,et al.L1-L2regularization based alternating optimal algorithm for image restoration.Computer Engineering and Applications,2014,50（3）：125-128.

CNKI网络优先出版：2013-06-08，http://www.cnki.net/kcms/detail/11.2127.TP.20130608.0956.014.html

1 引言

在采集、传输、存储和使用的过程中，数字图像的退化是不可避免的，退化图像主要表现为模糊和含有噪声。无论对研究还是应用而言，退化图像很难发挥其应有的价值。因此，需要一种技术可以去除图像中的模糊和噪声，获得清晰无噪声的图像（即所谓的原始图像）。图像复原正是在这种背景下出现的。图像复原分为图像盲复原和非盲的图像复原，前者重建原始图像时，同步对模糊进行辨识；后者模糊是已知的，直接重建原始图像。非盲的图像复原算法主要有：基于总变分（Total Variation，TV）模型的算法、基于Bregman迭代的算法和基于稀疏表示的算法。TV范式||∇·||1是TV模型[1]的关键，由于它的存在，基于TV模型的算法能有效保留复原图像重要的信息，如边缘、纹理等。但TV模型会导致图像出现阶梯效应（staircase effects）[2]，且它是不可微分的，给数值计算带来了困难。因此，一些高阶的TV模型[3-4]被提出，一定程度上克服了TV模型固有的缺点。Bregman迭代法最早由S.Osher等人[5]引入图像处理领域，主要针对TV正则化的图像复原问题。近年来，在传统Bregman迭代法的基础上，衍生出了线性Bregman迭代法[6]和分裂Bregman迭代法[7]等。借助Bregman距离，Bregman迭代法可将图像问题分解为等价的子问题求解。该类算法的优点是速度快、所需的迭代次数少，且容易编程实现。作为近年来出现的新技术，稀疏表示在图像复原领域已得到较广泛的应用。在稀疏表示的框架下，图像被表示为字典矩阵各列的线性组合，图像复原只需估计最优的线性系数向量（即原始图像的稀疏表示）。字典的选择对该类算法非常重要，早期多用正交小波基分解表示图像。为消除正交小波基给复原图像带来的块效应，M.A.T.Figueiredo等人[8]提出将超完备小波字典用于图像复原。此后，超完备小波字典成为稀疏表示复原算法的主流选择。小波变换的缺点是方向选择性差，曲波（curvelet）、轮廓波（contourlet）等新的表示方法克服了这一缺点。越来越多的算法采用曲波、轮廓波等分解表示图像，以获得更好的图像复原结果。正如F.X.Dupe等人[9]文章中所论述的，相比超完备的小波字典，这些新型的超完备字典更适用于图像复原。虽然图像复原时，许多优秀的算法仍倾向于采用预先给定的字典，但J.Mairal等人指出，这些预先给定的字典无法适用所有类型的图像，今后的算法将更多通过学习的方式获得所需要字典[10-11]。

本文提出了一种快速高效的图像复原算法，针对图像复原，借助稀疏表示理论，建立了一种通用的包含双正则项的复原问题模型。由于复原模型的目标函数不可直接微分，利用交替优化方法处理该模型，将其分解为更容易求解的子问题。最后通过实验验证该算法的有效性。

2 图像复原建模及其算法

观测图像与原始图像之间的关系可表示为：

式中，y∈Rm×1表示观测图像；线性算子A∈Rm×n表示模糊；x∈Rn×1表示原始图像；n∈Rm×1是加性噪声。观测图像y是已知的，原始图像x是未知的，图像复原的目的即获得x的最优估计，因此它属于线性反问题，需要为其建立适合的问题表示模型。

2.1 图像复原问题模型

本文为图像复原问题建立了如下模型：

式中，c∈Rl×1表示原始图像的稀疏表示；DT∈Rl×n表示超完备字典，可以是通过学习得到的也可以是预先指

定的；凸函数g1(x)和g2(c)为：

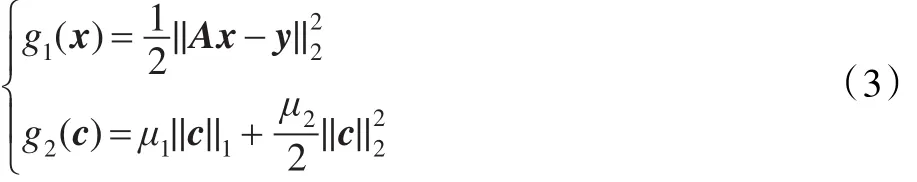
式中，μ1≥0，μ2≥0；L1范式 (||·||1)和L2范式 (||·||2)为目标函数的正则项。一些常见的模型，如Tikhonov模型[12]、基追踪降噪模型[13]和弹性网模型[14]等都可看做模型式（2）的特例。

由于目标函数J(x，c)含有两个未知量，优化问题式（2）无法直接求解，为避免同时存在多个变量，采用交替优化方法将式（2）分解为以下的子问题：

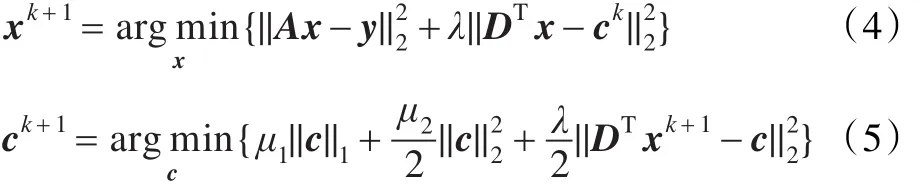
式中，λ≥0；k表示迭代次数。式（4）可直接求得：

因子问题式（4）的目标函数是连续可微的凸函数，因此式（6）得到的是子问题式（4）的全局最优解。当式（6）中的DT是Parseval框架小波时，满足DDT=I[15]，其中I表示单矩阵。

2.2 子问题式（5）的计算

由于L1范式的存在，子问题式（5）的目标函数不可直接微分。利用迭代重加权（iterative reweighted）方法[16]对其处理，该子问题可表示为：

对于第k+1次迭代，fk(ck)为常数。式（8）中，wk为：

式中，t表示阈值函数；τ表示阈值，其定义为：

将式（8）代入式（7），直接可得：

综上所述，本文提出的图像复原算法如下：

其中，ε≥0表示容许误差，是一个很小的常数。

3 实验结果

不失一般性，实验采用标准图像cameraman作为原始图像，如图1所示，该图像的分辨率为256×256。将图2中的模糊核分别作用于原始图像，在生成的模糊图像中加入标准差为0.5的高斯噪声，得到图3（a）、图 3（b）所示的退化图像。图3中，高斯退化图像和运动退化图像的峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）分别是21.07 dB和21.65 dB，PSNR是衡量图像质量的客观标准，一般PSNR值越大说明图像的质量越高。PSNR的定义为：

图1 原始图像

图2 模糊核（放大显示）

图3 退化图像

实验选择了Haar小波作为字典D，它是一种正交、紧支撑、对称的小波，有助计算变得更简单快速。参数的取值分别为：μ1=2.0E-3，μ2=1.0E-6，λ=2.5E-3。实验所用仿真软件为MATLAB R2011b，算法的运行环境为Windows XP SP3，2 GB内存和2 GHz的双核CPU。

本文所提算法被应用于处理退化图像，以验证其有效性。同时与A.Levin等人[18]和D.Krishnan等人[19]提出的算法进行比较，以评估本算法在速度和复原质量等方面的性能。Levin等人提出的是基于图像导数稀疏先验的复原算法，Krishnan等人提出的是基于稀疏超拉普拉斯（hyper-Laplacian）先验的图像复原算法，这两种算法均属于稀疏表示算法。三种算法对退化图像的复原结果如图4所示，为保证复原结果的客观性，表1给出了图4中所有复原图像相应的PSNR值，以及复原所需的时间和迭代次数。表1中的时间是每个算法运行10次所需时间的平均值，Levin算法的结果是基于稀疏先验得到的。

图4 退化图像复原结果

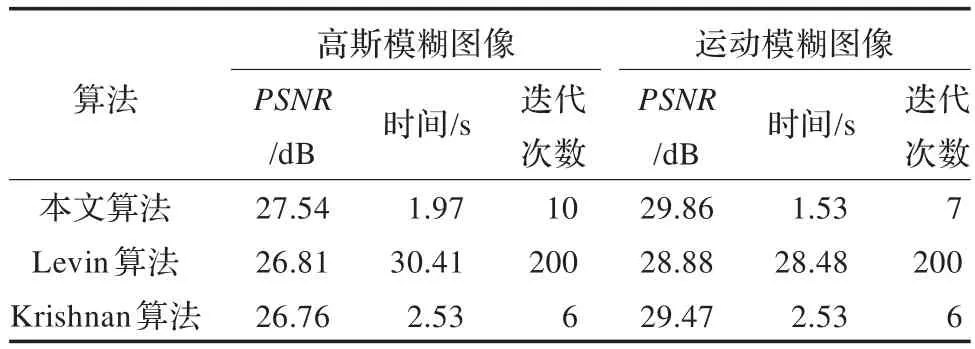
表1 退化图像复原结果比较

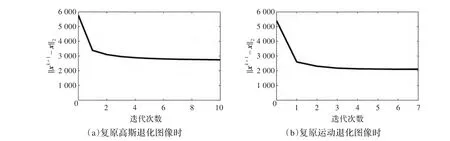
图5 本文算法的收敛情况

由表1和图4的结果可看出，在复原图像的质量和复原速度方面，本文所提算法优于Levin算法和Krishnan算法。仅需少量迭代，本文的算法即可获得较理想的结果，这与该算法良好的整体架构及子问题的处理策略有关。由于子问题计算的时间复杂度较低，加之Haar小波的简单高效，本算法具有较好的时间性能。Levin算法利用迭代重加权最小二乘法和共轭梯度法处理图像复原问题，所需共轭梯度迭代次数较多，限制了自身的速度。因此，图像复原的速度明显比本算法和Krishnan算法慢。上文已对本文算法的收敛性进行了简单分析，它在迭代过程中的实际收敛情况如图5所示。由该图可看出，在迭代过程中，||xk+1-x||2的值逐渐减小，说明本算法是不断地收敛的，这与上文的分析一致。

4 结束语

作为线性反问题，图像复原的难点在于提高复原质量的同时提高速度。针对此问题，本文提出了一种新的算法。结合稀疏表示技术，建立图像复原模型。在求解图像复原模型时，选择用交替优化方法将其分解为子问题。对于不可微分的子问题，采用迭代重加权方法处理。相比较而言，子问题的求解比原问题更简单。实验对高斯模糊和运动模糊的cameraman图像进行复原，并且与Levin和Krishnan算法进行比较，实验结果验证了本文算法的有效性，相比Levin和Krishnan算法，本文的算法在速度及复原质量方面更具优势。

[1]Beck A，Teboulle M.Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems[J].IEEE Transactions on Image Processing，2009，18（11）：2419-2434.

[2]Stefan W，Renaut R A，Gelb A.Improved total variationtype regularization using higher order edge detectors[J].SIAM Journal on Imaging Sciences，2010，3（2）：232-251.

[3]Goldfarb D，Yin W T.Second-order cone programming methods for total variation-based image restoration[J].SIAM Journal on Scientific Computing，2005，27（2）：622-645.

[4]Lysaker M，Tai X C.Iterative image restoration combining total variation minimization and a second-order functional[J].International Journal of Computer Vision，2006，66（1）：5-18.

[5]Osher S，Burger M，Goldfarb D，et al.An iterative regularization method for total variation-based image restoration[J].Multiscale Modeling&Simulation，2005，4（2）：460-489.

[6]Cai J F，Osher S，Shen Z W.Split bregman methods and frame based image restoration[J].Multiscale Modeling&Simulation，2009，8（2）：337-369.

[7]Setzer S，Steidl G，Teuber T.Deblurring Poissonian images by split Bregman techniques[J].Journal of Visual Communication and Image Representation，2010，21（3）：193-199.

[8]Figueiredo M A T，Nowak R D.A bound optimization approach to wavelet-based image deconvolution[C]//Proceedings of the IEEE International Conference on Image Processing.Piscataway，USA：IEEE Signal Processing Society，2005：782-785.

[9]Dupe F X，Fadili J M，starck J L.A proximal iteration for deconvolving Poisson noisy images using sparse representations[J].IEEE Transactions on Image Processing，2009，18（2）：310-321.

[10]Mairal J，Elad M，Sapiro G.Sparse representation for color image restoration[J].IEEE Transactions on Image Processing，2008，17（1）：53-69.

[11]Mairal J，Sapiro G，Elad M.Learning multiscale sparse representations for image and video restoration[J].SIAM Journal on Multiscale Modeling&Simulation，2011，7（1）：214-241.

[12]Lorenz D A.Convergence rates and source conditions for Tikhonov regularization with sparsity constraints[J].Journal of Inverse and III-posed Problems，2008，16（5）：463-478.

[13]van den Berg E，Friedlander M P.Probing the Pareto frontier for basis pursuit solutions[J].SIAM Journal on Scientific Computing，2009，31（2）：890-912.

[14]Zou H，Hastie T.Regularization and variable selection via the elastic net[J].Journal of the Royal Statistical Society：Series B（Statistical Methodology），2005，67（2）：301-320.

[15]Mallat S.A wavelet tour of signal processing：the sparse way[M].3rd ed.New York：Academic Press，2008.

[16]Daubechies I，Devore R，Fornasier M，et al.Iteratively reweighted least squares minimization for sparse recovery[J].Communications on Pure and Applied Mathematics，2010，63（1）：1-38.

[17]Combettes P L，wajs V R.Signal recovery by proximal forward-backward splitting[J].Multiscale Modeling&Simulation，2005，4（4）：1168-1200.

[18]Levin A，Fergus R，Durand F，et al.Image and depth from a conventional camera with a coded aperture[J].ACM Transactions on Graphics，2007，26（3）.

[19]Krishnan D，Fergus R.Fast image deconvolution using hyper-laplacian priors[J].Advances in Neural Information Processing Systems，2009，22.

XIAO Su,HONG Liurong,SHEN Ke,ZHENG Ying

School of Computer Science and Technology,Huaibei Normal University,Huaibei,Anhui 235000,China

For rapidly and accurately restoring images,a novel image restoration algorithm is presented.In the framework of sparse representation,a new constrained optimization model is created,which enables the estimations of the original image and its sparse representation.The objective function of the model hasL1-L2regularized terms,thus the alternating optimization method is introduced to decompose the model into equivalent sub-problems.The non-differentiable one among sub-problems is handled by iterative reweighted method.The experimental results demonstrate that with only a few iterations,the presented algorithm can achieve optimal estimations of the original image and its sparse representation.Compared with some state-of-the-art algorithms,the presented algorithm shows to be faster,and obtains better results.

image restoration;alternating optimization;sparse representation;regularization;iteratively reweighted method

为快速且准确地重建原始图像，提出一种新的图像复原算法。在稀疏表示的框架下，建立图像复原问题的约束优化模型，同步估计原始图像及其稀疏表示。复原模型的目标函数包含L1-L2双正则项，为此采用交替优化将模型分解为若干子问题，交替迭代求解这些子问题。其中不可微分的子问题，由迭代重加权方法进行处理。实验结果表明，仅需较少次迭代该算法即可获得原始图像及其稀疏表示的最优估计。与某些优秀的同类算法相比，该算法的速度更快，复原图像的质量更高。

图像复原；交替优化；稀疏表示；正则化；迭代重加权方法

2013-03-11

2013-04-27

1002-8331（2014）03-0125-04

A

TP391

10.3778/j.issn.1002-8331.1303-0128

国家自然科学基金（No.61070090）；安徽省高等学校省级自然科学研究项目（No.KJ2013B237）。

肖宿（1982—），男，博士，讲师，研究领域为数字图像复原；洪留荣（1969—），男，博士，教授，研究领域为模式识别与图像处理；沈克（1975—），男，副教授，研究领域为数字图像处理；郑颖（1982—），女，讲师，研究领域为数字图像处理。E-mail：smartwindows@sohu.com