基于核主成分分析的PSO—SVR的煤炭物流需求量预测
2014-06-10李博曾鸣
李博 曾鸣
摘要:利用核主成分分析法对煤炭物流需求影响因子进行特征提取,以获得的主成分作为支持向量机的特征向量建立支持向量机模型,利用粒子群算法对模型参数进行选择优化,从而构建出核主成分分析和粒子群优化支持向量机协同模型,并通过实例对模型的合理性和有效性进行验证。
关键词:核主成分分析;PSO-SVR;煤炭;物流需求预测
1.引言
煤炭是我国重要的基础能源,对其物流需求量进行科学预测,可以使煤炭物流供给与需求相匹配,从而避免物流基础设施的盲目投资,降低成本[1]。由于煤炭货运量在一定程度上能够反映煤炭物流需求规模变化,因此本文所研究的煤炭物流需求就是指煤炭的货运量。
本文利用支持向量回归机构建煤炭物流需求预测模型,并利用核主成分分析法与粒子群算法进行优化。通过预测我国的煤炭物流需求,为政府以及相关企业的决策提供参考,进而实现煤炭能源的可持续发展。
2.基于核主成分分析的PSO-SVR预测模型
2.1核主成分分析
设Rd为原始空间,其中有n个样本x1,x2,…,xn,构成数据矩阵X,通过非线性映射函数将其从Rd中映射到高维特征空间F中[2]。同时,将映射数据的均值设为0,即:
∑DDni=1DD)φxi)=0JY(1)
在特征空间F中,其协方差矩阵可以表示为:
CF=SX1nSX)∑DDnk=1DD)φxk)φxk)TJY(2)
对CF进行特征矢量分析,其特征矢量为V,特征值为λ,即λV=CFV。由定义矩阵K=[Ki,j]n×n,Ki,j=φxi)·φxj))可知,通过核函数可对其进行确定。设V的第k分特征矢量为Vk,通过归一化处理,VkVk=1,可得到特征矢量Vk中映射数据φx)的投影为:
[Vk·φx)]=∑DDni=1DD)αki[φxi)·φx)]JY(3)
综上推导是在映射数据均值为0的基础上开展的,而这一假设在实际中几乎不存在,因此,有必要对映射数据进行中心化,即用AKK-来代替K:
AKK-=K-InK-KIn+InKInJY(4)
其中,In是n×n的矩阵(n为样本数目),且满足Ii,j=1/n。因此,样本数据第k维非线性主成分为:
tk=VFTX-·φx)
=∑DDni=1DD)αkiTX-AKK-xi·x)JY(5)
2.2PSO-SVR模型
支持向量机(SVR)是指将输入向量数据映射到高维特征空间中,建立最优决解函数,并利用原来核函数代替高维特征空间中点积运算,通过有限样本学习,搜索全局最优解[3]。支持向量机的估计函数为:
fx)=WTφx)+bJY(6)
应用不敏感损失因子ε转化估计函数为优化问题,即:
minDDXw,b,ξ,ξ*DD)SX12SX)WTW + C∑DDli = 1DD)ξi + C∑DDli = 1DD)ξ*i JY(7)
约束条件为:
JB{WTxi ) + b-yi ≤ε + ξi yi -WTxi )-b≤ε + ξ*i JB),ξi ,ξ*i ≥0,i = 1,…lJY(8)
式中,b是偏置量,是松弛因子,C是惩罚因子。
利用对偶理论将式(8)转化为二次规划进行求解,其对偶式为:
minDDXα,αDD)SX12SX)α-α)TQα-α)+ε∑DDli=1DD)α+α)+∑DDli=1DD)yiα-α)JY(9)
约束条件为:
∑DDli=1DD)α-α)=0,0≤αi,αi≤C,i=1,…,lJY(10)
其中,Qi.j=Kxi·x)≡φxi)·φxj)
通過二次规划算法可得SVR回归预测模型为:
∑DDli=1DD)-α+α)Kxi·x)+bJY(11)
利用粒子群算法(PSO)对SVR的参数进行优化。PSO是全局优化算法中的一种,在一个D维搜索空间中,N个粒子构成一个群落,其中,每个粒子均表示一个候选解。同时,粒子还具有一个速度来决定其飞行的距离与方向。粒子们追随着当前最优粒子在D维空间中搜索极值,即全局极值与个体极值。找到这两个极值后,粒子根据式(12)和式(13)来更新其位置与速度[4]:
vk+1id=ω×vkid+c1r1pkid-xkid)+c2r2pkgd-xkid)JY(12)
xk+1id=xkid+vk+1idJY(13)
式中,vk+1id是第i个粒子在k+1代的飞行速度,vid∈[-vmax,vmax],vmax是常数。ω为惯性权重,i=1,2,…,N,d=1,2,…,D;c1,c2为非负常数,称为加速因子,根据经验,通常c1≠c2,r1和r2是介于[0,1]之间的随机数。
在PSO-SVR模型中,需要优化支持向量机中的不敏感损失因子ε与惩罚因子C。选取参数ε较小的值为初始值,利用PSO优选模型参数,不断搜索均方误差最小的参数对,提高参数ε的值,直到满意为止。进而提高预测的准确度,优化SVR模型。
3.我国煤炭物流需求预测的实证分析
3.1建立煤炭物流需求影响因素指标体系
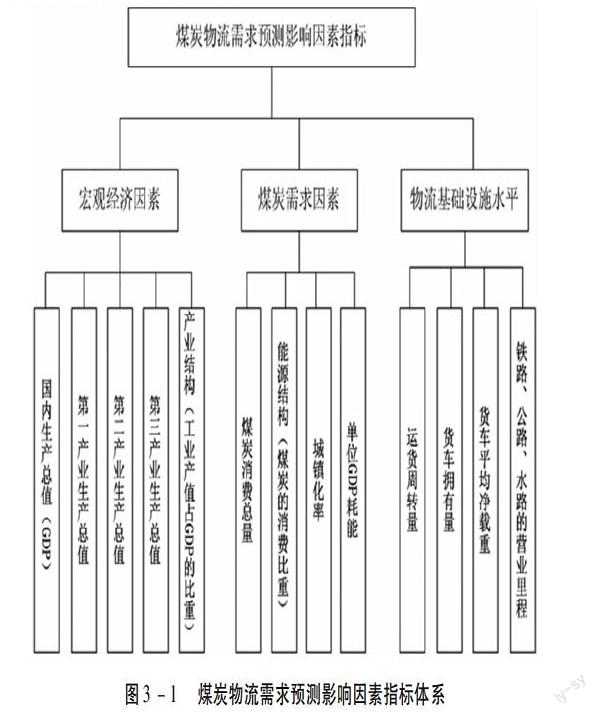
影响煤炭物流需求因素十分广泛且复杂[5]。煤炭需求受经济规模、宏观经济政策、消费观念、煤炭运输网络、消费水平、物流服务水平等诸多因素的影响[6]。本文将尽可能从不同方面进行分析,建立煤炭物流需求预测影响因素指标体系。如下所示:
李博.TIFTS(JZHT7.H图3-1煤炭物流需求预测影响因素指标体系TS)KH*2
3.2利用模型进行煤炭物流预测
以1995-2011年我国煤炭物流货运量为预测对象,结合指标体系中所提出的13个影响因子,利用本文所提出的基于主成分分析的PSO-SVR对我国煤炭物流需求进行预测,其详细流程如下:
(1)利用核主成分分析法选取物流需求预测的主要影响因子。设置KPCA核函数为高斯径向基核函数,主成分方差计贡献率如图3-2所示,为了尽量包含数据的全部特征,本文取前五项主成分,其累计贡献率达0.987。因此,本文最终选定的煤炭物流需求预测影响因子为:运货周转量、煤炭消费总量、城镇化率、货车拥有量、产业结构(工业产值占GDP的比重)。详细数据如表3-1所示。
李博2.TIFTS(JZHT7.H图3-2主成分方差累计贡献率TS)KH*2
表3-1煤炭货运量与影响因素数据
(2)设训练样本为1995-2007年的煤炭货运量和其影响因素,测试样本为2008-2011年的数据。
(3)对样本数据进行归一化,公式如下所示:
JZxi=SXxi-xminxmax-xminSX)
JZyi=SXyi-yminymax-yminSX)
(4)利用PSO优化模型参数。设初始粒子群的群体数量为30,惯性权重ω为0.6,学习因子c1与c2分别为1.2和2,,最大迭代步数为100。搜索得到支持向量机的参数,其中RBF核函数参数γ=0.241,惩罚因子C=8.825。应用计算获得的模型参数,构建煤炭物流需求与影响因素之间的非线性响应模型。
(5)利用所建立的模型对测试样本进行预测,检验模型的有效性和预测能力。
预测结果如表3-2所示。
由表3-2可知,KPCA-PSO-SVR模型在煤炭物流预测过程中,相对误差处于1%左右,这说明该模型的拟合能力是比较好的。2008-2011年,模型的预测相对误差分别为0.88%、0.95%、1.01%和1.15%,精度虽均满足要求,可是却是在逐步下降的,这表明该模型具有较强的泛化能力。KPCA-PSO-SVR模型对整个时序数据月的平均绝对误差为1500.75吨,平均相对误差为1%,综合展示了该模型在煤炭物流需求预测中较好的拟合和泛化能力。
4.结语
本文针对煤炭物流的复杂网络特性,建立煤炭物流需求影响因素指标体系,将核主成分分析法(KPCA)与粒子群优化的支持向量机(PSO-SVR)相结合,提出了适用于小样本量研究的基于核主成分分析的PSO-SVR预测模型,并进行实证分析,结果表明:在解决我国煤炭物流需求预测这种非线性、小样本、高維模式识别问题中,KPCA-PSO-SVR煤炭物流需求预测模型是—个比较有价值的预测模型。(作者单位:华北电力大学经济与管理学院)
参考文献:
[1]李琰,李红霞.我国煤炭物流产业评价体系的构建[J].统计与决策,2012(15):182-183.
[2]于红芸,姜涛,关键.SAR图像的快速核主成分分析识别方法[J].中国图象图形学报,2012,17(1):137-141.
[3]耿立艳,赵鹏,张占福.基于二阶振荡微粒群最小二乘支持向量机的物流需求预测[J].计算机应用研究,2012,29(7):2558-2560.
[4]Guzzetti F,Peruccacci S,Rossi M,etal. The rainfall intensity–duration control of shallow landslides and debris flows:an update[J]. Landslides,2008,5(1):3-17.
[5]王莹莹.基于灰色神经网络模型的煤炭物流需求预测研究[D].北京交通大学,2012.
[6]赵光.煤炭需求影响因素及情景分析[J].煤炭经济研究.2011,31(11):18-20.
