基于电场逆问题的高压输电线电压传感器技术与试验研究

高 参，汪金刚，范禹邑，朱丽云

(重庆大学输配电装备及系统安全与新技术国家重点试验室，重庆 400044)

0 引言

电压互感器的准确性、便利性和快速性对智能电网中的电能计量、系统监测诊断和电力系统故障分析等方面起着非常重要的作用。目前，我国高压及超高压电网中普遍采用的是电磁式电压互感器(Potential Transformer，PT)和电容式电压互感器(Capacitive Voltage Transformer，CVT)。传统的电磁式电压互感器具有体积大，绝缘难度随着电压等级提高而增大等问题[1]。相对于PT，CVT具有绝缘结构简单、性价比高、易维护等优点。但由于CVT 带有耦合电容、中间变压器和补偿电抗器等内部储能元件，所以其暂态响应较差，并且在高频过电压下，二次侧容易发生由铁磁谐振引起的高频振荡，威胁了设备的安全运行[2-3]。同时，CVT和PT一样，有着输出无法和计算机直接相连、容量有限、频带较窄等问题[4-5]。这些问题使得二次侧的电能计量和继电保护面临极大的挑战。

在此，提出了通过感应电荷法测得电场，再进行电场逆问题计算，最终测得电压的新思路，并研制出一款新型电子式电压互感器。新研制的基于电场逆问题的电子式电压互感器具有传统电磁式互感器难以比拟的优势：从输入到输出并没有与地线有实际的电气连接，杜绝了有接地电流流过测量系统而对二次侧造成损坏，也不用考虑对地绝缘问题，实现了小型化、非接触式数字化测量；其信号测量的精度和运行稳定性是数字化变电站安全稳定运行的重要保障，对智能电网的构建也具有积极意义。

从全球角度看，电子式电压互感器是当今研究的热点和前沿课题，是数字化电力系统、数字化变电站和数字化发电厂建设的关键设备之一，也是未来互感器技术发展的新方向。另外，针对目前新能源开发中，大型风电网中存在的电压快速波动、闪变和高次谐波等严重的供电质量问题，需要研究风力发电系统中电压、电流快速波动的有效监测方法，以满足在大规模风电并网背景下，对测量动态变化范围很宽的电流、电压信号给予有效、准确测量的需要。因此，研究和开发新原理的电子式电压互感器必然具有前瞻性和战略意义。

1 传感器的设计原理

1.1 电场逆问题计算原理

实际输电线中负载变化等因素会造成输电线电位发生偏差，因此为测得其电位大小需引进电场逆问题解决方案。

根据工频电磁场数值分析：可采用模拟电荷法求解输电线附近电场。在输电线等效模型中，首先要计算模拟电荷的大小，由于无法通过直接求解方程来得到模拟电荷的大小，此时采用最小二乘原理将逆问题的求解换成极值问题的求解。设其正问题非线性算子为F(q)，q为模拟电荷的大小，E为测量点的电场强度，逆问题可描述为

与式（1）对应的最小二乘方程为

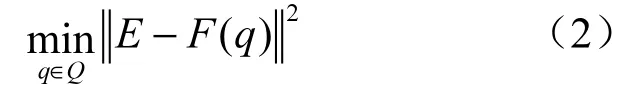
在工程实际测量中，为了更准确地测得输电线周围电场分布，测量点的个数都会大于模拟电荷数，所以此时的方程（2）为超定方程。式（2）的非线性最小二乘问题，可用到分段线性化迭代算法来实现。首先对非线性算子F进行近似，采用泰勒公式将F(q+δq)在q处展开并忽略其高阶无穷小量时有

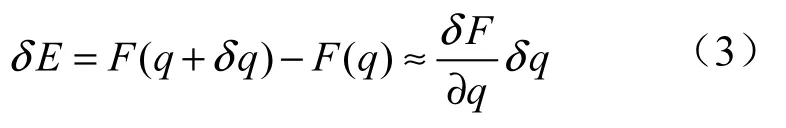
由此，可得到Eδ与qδ之间的线性关系为

设*q=q+qδ是式（1）的准确解，则在靠近q*的q处，可以根据式（3）得出qδ的线性算子方程为

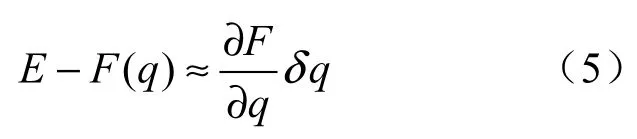
式（5）构成了求解非线性方程组的基础。则对于式（2）的最小二乘问题，q取得极小解的必要条件是q的梯度g(q)=0，令式（2）中的目标函数为φ，即则将其展开为

式中，J为对应的雅克比矩阵。上式为非线性最小二乘问题的法方程，因此结合式（5），非线性最小二乘法的求解就是对式（6）的求解。此式仍为非线性方程，需引进Hessian矩阵H(q)，通过求解hessian矩阵，得到q的极小值，将并将其代入目标函数可计算出目标函数，求得导线电荷q。根据电磁场原理，导线电荷正比于导线电位，因此可得电位值。

1.2 传感器设计计算原理

针对特定环境——输电导线附近，其受邻相和地面物体的影响很小，并忽略环境温、湿度对测量的影响，其电场将呈较强规律分布，所以，逆问题计算只需要进行一维求解。加之在实际工程测量中，高压输电导线的长度远远大于传感器和导线之间的距离，因此可将输电导线看作是无线长直带电线，并规定无穷远处电位为0。

将传感器放置于输电导线附近固定位置，处于交变电场中的传感器，在其表面会产生感应电荷，在传感器两极间接入测量电容元件CM，感应电荷在在测量电容上产生的电压UM(t)与场强E0(t)的关系为

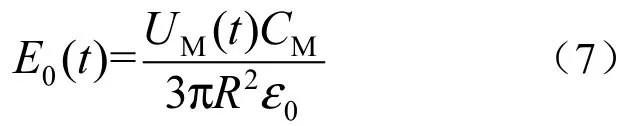
式中，R为传感器半径。

由式（7）可知，由传感器测量电容上的电压UM(t)就得到传感器所处位置的电场强度E0(t)[5]。

根据电磁场原理，无线长直导线上电荷量q(t)与导线外一点P（传感器所在位置）的场强E0(t)的关系为[6]

式中，ρ为导线与传感器的距离。

将式（7）代入式（8），可由传感器测量电容电压UM(t)得到导线的电荷q(t)为

由前一节电场逆问题计算原理可知，导线表面电位ϕ(t)∝q(t )，即可换算得到导线电压U(t)：

最后经过多次试验测量后，再进行数据标定，确定正比例的K值大小，获得导线电位值。

2 传感器装置的设计

2.1 硬件结构的设计

设计的传感器模型如图1所示，它主要由传感器极板、信号采集处理单元、无线传输模块以及数据接收终端等组成。

图1 电压传感器结构模型Fig.1 Structure model of voltage transformer

相对于平行板型、盒型等结构，传感器的前端在设计上采用了类似球型的极板结构。将一个金属的球型导体沿着其中心线分成上下两部分，分隔后的上下两个半球为传感器的两个电极，并通过一个测量电容与他们相连。再让被测高压输电导线穿过该传感器圆心。如此，可准确计算表面电荷与电场，并且还可粗略计算其畸变影响。采用此结构还具有电场畸变相对较小的优点[7]。

传感器工作流程是：首先，将传感器极板感应电荷形成的电流进行I-V转换为电压信号，再利用差分放大器 AD620进行放大，AD620保证了对微弱电压信号的差模放大倍数和高共模抑制比；然后采用低通滤波器进行高频滤波，截止频率为1 kHz；再进行信号调理，输入单片机中AD转换成数字信号，数据采样频率为12 kHz，再根据算法进行数据换算处理；最后，将电压数据通过WiFi模块与接收端进行数据交换，WiFi模块数据传输速率为1 Mbps，满足数据传输要求。接收端接收到数据信息后，对其进行二次转换和数据处理，最后以数字和模拟信号形式输出给二次设备。

2.2 传感器设计误差分析

传感器电极在电场中其表面电荷会发生移动，从而会造成周围电场的畸变。因此，电场测量应该考虑如何降低由于传感器引入到被测场后造成的电场畸变。由于传感器被置于高压环境下，其所处位置的空间电位很高，因此上下两个半球之间的电位差很小，可以忽略不计。因此假设两个半球是等电位，在这种情况下就可等效于将一个完整的金属球放置在强电场中。下面将对这一问题进行畸变分析。

如图2所示，将金属球型传感器置于一个无限大的均匀电场中，未受畸变的均匀电场为E0，无限大空间的介电常数ε1。传感器内部填充的绝缘物质的介电常数为ε2，传感器的半径为r0，传感器外某点M与原点O的距离为r ，与电场方向的夹角为θ。

图2 位于均匀电场的球型传感器Fig.2 Spherical sensor in a uniform electric field

引入测量传感器后，会使其周围空间的电场强度发生畸变。引入球型传感器造成的畸变电场为

当θ=0时，畸变电场达到最大值：

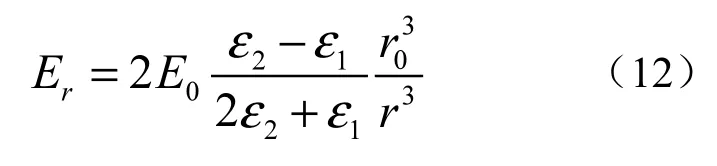
对于给定的一个传感器，式（12）中ε1、ε2均为常数，的大小决定了畸变电场值。因此，想要使电场的畸变越小，就要选取较小的传感器半径r0，且要增大传感器与导线的距离r。实际测量中，为了将电场畸变造成的误差控制在指定范围内，应尽量采用小尺寸的传感器，且传感器与导线之间的距离应限制在适当的范围内[8]。

3 模型测试与数据分析

3.1 高压试验平台

为了验证传感器的测量准确度，建立了一个高压试验平台，如图3所示，电压控制箱控制升压变压器的电压输出，变压器的输出接一直铜棒作为长直输电导线。传感器外接有测量电路，可以显示被测电场值或被测电压的有效值。将测得的结果，通过无线传输技术传输到信号接收装置。试验分两步进行：首先将电压传感器放在与传输导线不同距离处进行电场测量（电压有效值）和畸变试验[9]；其次，可以用高压探头分压器同步测量电压波形，进行电压波形准确度的试验。

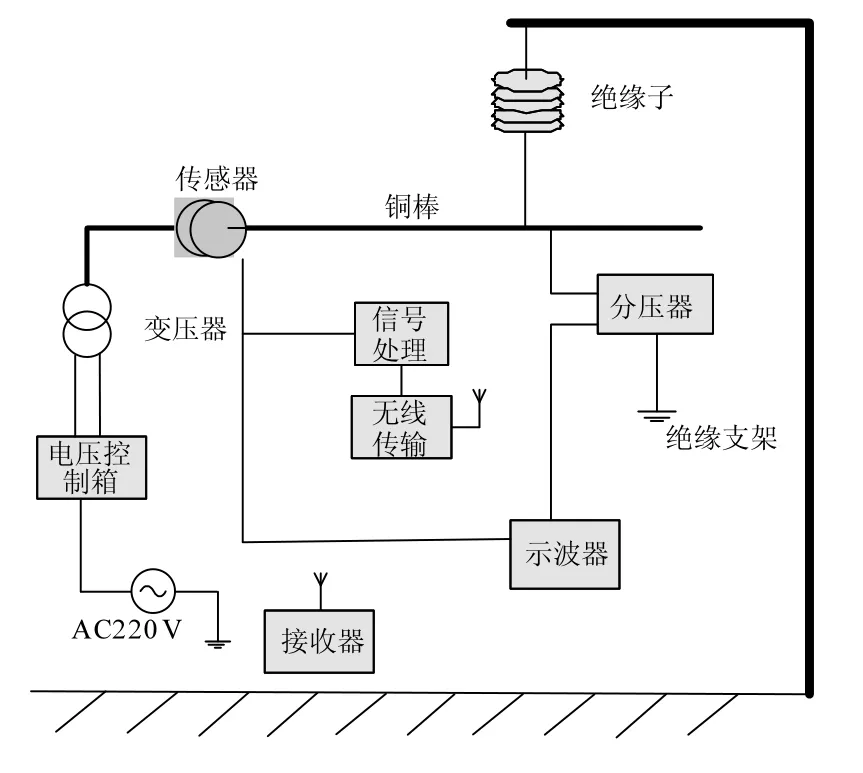
图3 高压试验平台图Fig.3 Test platform of high voltage

3.2 电场测试与畸变影响试验

采用上述高压试验平台，改变传感器与高压线的距离(40 cm、60 cm和80 cm)，并分别缓慢按试验规定调节变压器输出，每次递进值约为1 kV(从3 kV到10 kV)，记录标准检测装置和传感器测量的平均场强值，该场强值即对应着场源（高压导线）电压有效值，通过该试验来验证电压与场强的关系，以及不同距离下电场畸变对传感器所测电场准确度的影响。

试验结果如图4所示，可以看出：

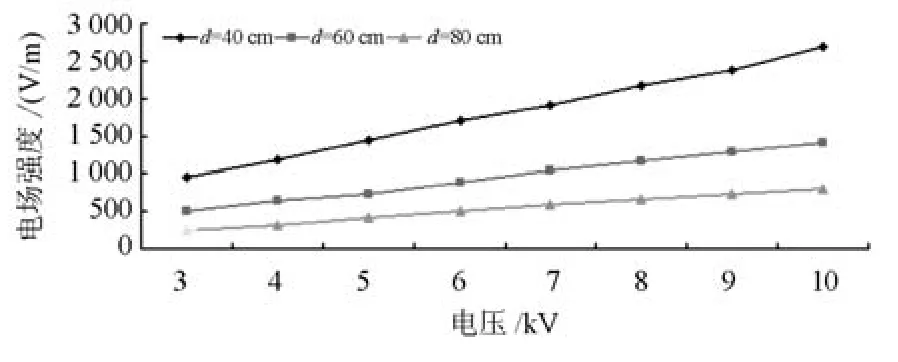
图4 不同距离下场强与电压数据关系Fig.4 Mathematical relationship between electric field strength and voltage of different distances

1）每个距离下，场强值与施加的电源电压基本呈线性关系。当距离不同时，两者之间关系曲线的斜率变化不大。这说明，传感器在不同距离下，受畸变的影响不大。

2）畸变影响较小且在误差允许范围内，最终得到的电压与电场的测量值，验证了基于电荷法测量电场强度，再逆推即时电压方法的可行性，也说明了该传感器的可行性。

3.3 交流电压测试对比试验

设计了一种电压传感器模型，外观如图5所示，传感器为圆柱形，分别为内外两层铜片，中间为环氧树脂。将传感器套在铜导线上并紧固之后，调整变压器，输入10 kV的交流电压。然后通过检测装置测量传感器输出的电压波形，并且使用高压探头同步测量变压器输出导线上电压，将两者的波形在手持式示波器显示。

图5 传感器模型结构和外观Fig.5 Structure and appearance of transducer

然后，将传感器测量的电压波形与分压器测得实际波形进行比较，比较两者相对幅度和相位，以验证传感器的电压测量准确度[10-13]。高压探头型号为Tektronix P6015 A，其时基精度达到0.75%，垂直精度为1.5%，其输出可以作为试验标准对比信号。

图6为10 kV交流电压下分压器测量的电压波形和传感器输出波形图。可见，与分压器测得的波形（CH2）相比，传感器测得的电压波形（CH1）的失真度较小，且相位误差和电压有效值的测量误差也较小。

图6 10 kV交流电压测量波形对比图Fig.6 10 kV AC voltage waveform comparison

导线上所加电压Un分别为额定电压10 kV的20%、40%、60%、80%、100%、120%时，测量高压探头与传感器的输出电压值及其计算得到的比差、角差如表1所示。其中UHV为高压探头折算至一次侧电压，UM为传感器测量电压。所用分压器的变比为100:1。

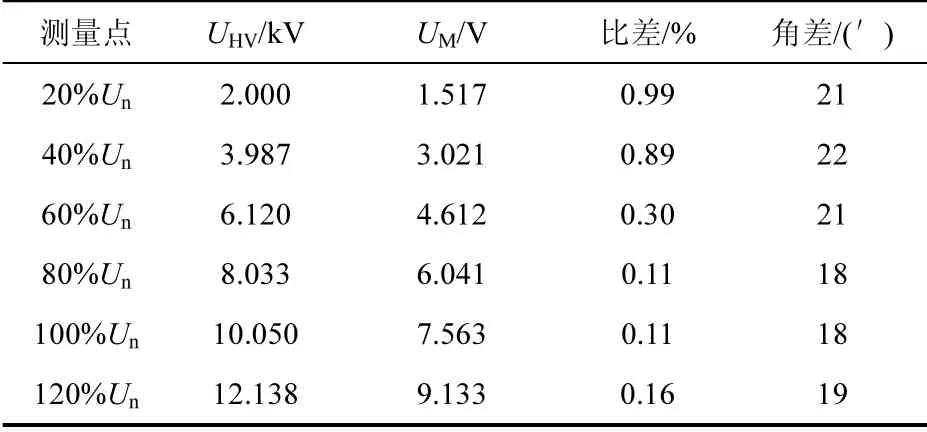
表1 传感器准确度测试结果Table 1 Accuracy test results of transducer

由以上测试结果表明：

1）传感器测量精度较高，在标准规定的80%～120%额定电压范围内，传感器可以达到0.5级的计量要求。对表1的电压数据进行一次拟合，其平方误差R2=0.014＜＜0.99，表明传感器测量电压与实际电压保持严格的线性关系。

2）从图6中波形和表1中相位误差数据可以看出，两者在相位上存在一定偏差，相位的误差范围最高达到22′，说明传感器在相位上误差较大。分析出现该问题的原因，该传感器是通过电容式感应电荷实现的，故存在固有的相位偏差。下一步将对传感器进行相位补偿等方面的研究。

4 结论与展望

通过电场逆问题计算，设计了一种基于电场逆问题的电子式电压传感器。试验结果表明，在此特定环境下，测量长直输电导线上电压时，该电压传感器受电场畸变影响较小，测得的电压有效值具有较高的准确度，传感器测量电压的波形失真度也很小。研究方法和设计的电压传感器具有一定的使用价值和进一步研究的价值，但波形相位还存在一些问题。

下一步研究中将进行传感器在复杂环境中的研究，考虑温、湿度对测量的影响，周围不同环境介质对测量的影响。传感器高电位端供电、传感器相位补偿等工作使其能满足工程设计需要。

[1] 许韦华, 鲍海, 杨以涵, 等.压电陶瓷式电子电压互感器的信号处理方法[J].电力系统保护与控制, 2010,38(10): 48-51.

XU Wei-hua, BAO Hai, YANG Yi-han, et al.Signal processing methods of piezoelectric ceramic electronic voltage transformer[J].Power System Protection and Control, 2010, 38(10): 48-51.

[2] 季遥遥, 李岩松, 刘君, 等.基于闭环负反馈高精度电流光学传感器技术的研究[J].电力系统保护与控制,2010, 38(19): 165-169.

JI Yao-yao, LI Yan-song, LIU Jun, et al.Study on the high precision optical current transformer based on closed loop negative feedback[J].Power System Protection and Control, 2010, 38(19): 165-169.

[3] 李丽芬, 朱永利, 黄建才, 等.基于无线传感器网络的绝缘子泄漏电流在线监测系统[J].电力系统保护与控制, 2011, 39(10): 74-79.

LI Li-fen, ZHU Yong-li, HUANG Jian-cai, et al.Wireless sensor networks based insulator leakage current on-line monitoring system[J].Power System Protection and Control, 2011, 39(10): 74-79.

[4] 杨帆.输变电设备工频电场的正、逆问题及电磁环境研究[D].重庆: 重庆大学, 2008.

YANG Fan.Study on forward and inverse problem of power frequency electric field of transmission and distribution apparatuses and power frequency electromagnetic enviroment[D].Chongqing: Chongqing University, 2008.

[5] 汪金刚, 林伟, 李健, 等.电容式交变电场传感器与工频电场检测试验研究[J].传感器与微系统, 2010, 29(9):21-23, 26.

WANG Jin-gang, LIN Wei, LI Jian, et al.Study on capacitive alternating electric field sensor and detecting test on power frequency electric field[J].Transducer and Microsystem Technologies, 2010, 29(9): 21-23, 26.

[6] 俞集辉.电磁场原理[M].2版.重庆: 重庆大学出版社,2007.

YU Ji-hui.Principles of electromagnetic field[M].Second Edition.Chongqing: Chongqing University Press, 2007.

[7] 刘聪汉.工频电场测量方法及安全警示系统设计研究[D].重庆: 重庆大学, 2012.

LIU Cong-han.Research on measurement method and safety warning system design of power frequency electric field[D].Chongqing: Chongqing University, 2012.

[8] 胡泽文.工频电场测量方法和传感器的研究[D].重庆:重庆大学, 2010.

HU Ze-wen.Research on the method and sensor of power frequency electric field measurement[D].Chongqing: Chongqing University, 2010.

[9] 钱政.有源电子式电流互感器中高压侧电路的供能方法[J].高压电器, 2004, 40(2): 135-138.

QIAN Zheng.Power supply for high voltage circuit of active electronic current transformer[J].High Voltage Apparatus, 2004, 40(2): 135-138.

[10] FESER K, PFAFF W, GOCKENBACH E.Distortion-free measurement of high impulse voltage[J].IEEE Trans on Power Delivery, 1988, 3(3): 857-866.

[11] SCHWAB A J, PAGEL J H W.Precision capacitive votage divider for impulse voltage measurement[J].IEEE Trans on Power Apparatus and Systems, 1972, 91(6):2370-2390.

[12] 余春雨, 叶国雄, 王晓琪, 等.电子式互感器的校准方法与技术[J].高电压技术, 2004, 30(4): 20-21.

YU Chun-yu, YE Guo-xiong, WANG Xiao-qi, et al.Calibratiom technique of electronic instrument transducers[J].High Voltage Engineering, 2004, 30(4):20-21.

[13] 吴涛, 周有庆, 龚伟, 等.基于新型电子式电流互感器的多功能电能表的设计[J].电力系统自动化, 2008,32(16): 56-60.

WU Tao, ZHOU You-qing, GONG Wei, et al.Design of multifunction watt-hour meter based on the new electronic current transformer[J].Automation of Electric Power Systems, 2008, 32(16): 56-60.