光子相关法测量空气声场中的粒子振速

李良杰， 何龙标， 王雪晶

（1.北京化工大学信息科学与技术学院，北京 100029；2.中国计量科学研究院，北京 100029）

光子相关法测量空气声场中的粒子振速

李良杰1， 何龙标2， 王雪晶1

（1.北京化工大学信息科学与技术学院，北京 100029；2.中国计量科学研究院，北京 100029）

声场中的粒子振速是评价空气声场特性的一个重要参量。在平面波声场中，通过获取激光多普勒测速仪对不同声压级声场中散射粒子产生的光电信号，采用光子自相关法对原始多普勒信号进行处理，粒子的速度量值根据相关函数的时间特征值得出，并与传声器测量声压值计算的粒子振速值进行比较。在原有自相关算法的基础上，利用样条插值法来估计相关周期，减小原有信号频偏与多普勒频率之比并非整数倍的引入的差异。实验结果表明，光子相关法能够获得声场中的粒子振速，与传声器测量值吻合较好，当振速较大时，插值法有利于减小测量偏差。在96～110 dB的声压量值范围内，光子相关法与传声器测量值之间的振速偏差优于0.7 dB。

计量学；粒子振速；声场；激光多普勒；自相关法：插值法

1 引 言

激光多普勒测速是根据多普勒原理，利用被测流体中的散射粒子对入射光进行散射，通过光电探测器探测散射光的频移量，由频移量计算出流体速度，具有非接触测量且实时性好等优点［1，2］。传统激光多普勒系统在结构上，入射光的双光束没有频率差别，无法获得流场的速度方向信息。目前大部分激光多普勒测速系统均加入了声光器件，使得两束入射光具有一定的频率偏差，用来鉴别流场的速度方向。空气声场是一种特殊流场，一方面粒子振速是周期变化的，频率取决于声源的振动频率；另一方面声场粒子振速通常量值较小，为毫米每秒量级。声场中粒子穿越激光多普勒干涉条纹所在的区域形成多普勒信号，其速度解调方法有别于传统的流场速度信号解调。Taylor K J等人采用频谱分析法，通过分析频域信号来获取流场特性，该方法常适合信噪比较高的声场，在本课题组前期工作中也得到了验证［3～5］。Greated C A等人采用光子相关技术，一定程度上克服了频谱分析法的缺点，但他们着重描述的是入射光无频差时驻波管声场中的粒子速度测量及信号解调方法，针对入射光束存在频差时的信号解调技术则涉及较少［6～8］。

本文在平面行波声场中，通过利用带频移技术的激光多普勒测速系统获得光电信号，采用自相关法对原始多普勒信号处理，对测量结果与传声器测量声压值计算得到的粒子振速进行比较，评价了自相关法的特点及适用性，并在原有基础上通过插值法来估计周期数，减小了粒子在振速较大时的测量偏差，为激光多普勒技术复现空气声压量值的方法研究奠定基础。

2 激光多普勒测速原理及信号的自相关处理

激光多普勒测量声场粒子振速的原理如图1所示，由激光器产生一定强度的激光，经由分光镜和反射镜分成汇聚至透镜，其中一束光经过声光调制器，与原始光产生一定频差。两光束在测量区域处形成明暗相间的干涉条纹，当粒子以一定速度穿过该区域时，散射光由光电接收器接收，转化成电信号，通过信号处理技术来解调粒子振动速度。

图1 激光多普勒测量声场粒子振速的原理框图

粒子速度与多普勒频移有着如下关系：

式中，df为测量区域干涉条纹间距；f是入射光与散射光的频移，也称多普勒频率；λ为波长；θ为双光束的半角。

式中，V是粒子速度。

对于多普勒信号时间间隔为τ的自相关函数［9］可以表示为：

式中，u0是流体平均速度，um是粒子速度，β＝cosθ／d，d为聚焦激光束的有效直径，J0为零阶贝塞尔函数。

当激光的双光束没有频偏时：

式中，τmin是自相关函数下降至第一个最低点时间。

对于双光束有频偏时，固有频偏可以看做流体平均速度导致的频移，通常粒子振速产生的频移要远小于双光束之间的频偏。因此，cos（Du0τ）J0（Dum）实质上是cos（Du0τ）对零阶贝塞尔函数的调制［10］，在贝塞尔函数取得零值时，其相应乘积的幅值也逐渐降为零。零阶贝塞尔函数的第一个根为2.405，因此，式（3）取得第一个最小值时，满足：

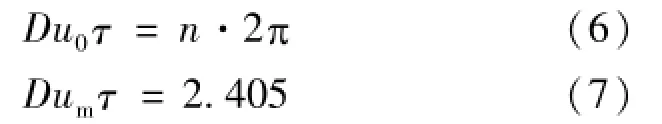
为了增大多普勒测速的动态范围，通常双光束的固有频偏较高，信号处理时，往往通过向下混频减小数据处理的工作量。此时，粒子速度可以表示为：

式中，Vmin为向下混频产生的等效速度，n为贝塞尔函数下降至第一个最低点时包含周期性波动的周期数。

3 实验装置

根据平面行波声场粒子速度和声压的关系：p＝ρcv，p为声场声压，ρ为介质密度，c为声速，v为粒子振速。图2为平面波声场中粒子振速测量的实物图，平面行波管尺寸为320 cm×10 cm×10 cm，末端带有吸声尖劈，提供一个较为理想的平面行波声场。测量传声器采用B＆K 4192。檀香燃烟作为示踪粒子，采用TSI公司的多普勒测速仪，干涉条纹间距为3.74μm，声光调制器频偏为40 MHz。在94～110 dB的声压级范围内，根据平面波声场特性，粒子振速范围为4～25 mm／s，对应的多普勒频率范围为：1 070～6 685 Hz。

图2 平面波声场中粒子测速实物图

4 实验结果及分析

实验中平面波声场由频率500 Hz正弦信号发生器产生，声阻抗z＝ρc。由于光电信号产生40 MHz的移频，因而能够辨别粒子运动方向。根据实际需求，信号通常向下混频至适合数据采集与处理的频带。图3是混频至50 kHz的多普勒信号，对应声压级为100 dB。

图3 频移为50 kHz的原始多普勒信号

本文中分别将信号向下混频至50 kHz和150 kHz，数字示波器采样率为1 MHz，对获得的信号进行自相关处理，最后估计自相关函数（ACF）包络线下降至第一个最低点时所包含调制信号的周期数获得粒子振速。图4为多普勒信号自相关结果，粒子振速量值根据式（8）可以得到。同时，将得到的速度值与传声器测量声压量值所对应的速度进行比较。图4中，相关信号由频移为50 kHz正弦信号调制，为统计自相关信号下降至第一个最低时统计相应的周期数，其最大值为特征点的包络曲线如图5所示，n＝11。

图4 频移为50 kHz的多自相关图

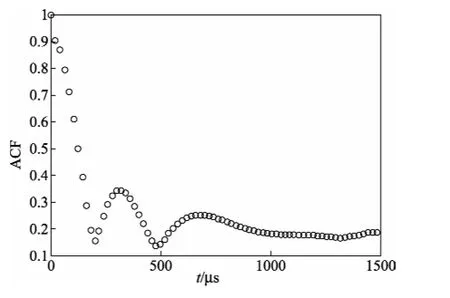
图5 频移为50 kHz自相关信号周期取点图

调节与平面行波管中扬声器相连的功放增益，便可在行波管内获得不同大小的声压级。图6中的声压级（SPL）量值介于96～111 dB之间，对应的速度（v）区间范围在为4～25 mm／s，粒子振速在声场中随着声压级增加逐渐增大，从整体上看，自相关法求得的速度与传声器测量声压值对应的粒子速度有着较好的一致性。在声压级较低时，传声器与相关法测量的结果能得到很好的吻合。随着粒子速度增大，两者的偏差也逐渐增大。声压级为109.11 dB时，两者速度有0.70 dB的差异。

图7中的频移量是图6频移的3倍，两者相比，150 kHz的频移表现出更好的稳定性，主要原因在于相同速度下，相同时间段内周期点数较多，速度变化间隔较小，带来的误差较低。在110 dB时，两者速度偏差减小为0.54 dB。另外，由式（8）可知，在强声场条件下，粒子振速较大时，应该取更大的频移信号，确保自相关函数在下降到第一个极小值时具有一定数目的调制周期。

图6 频移为50 kHz时的测量结果对照

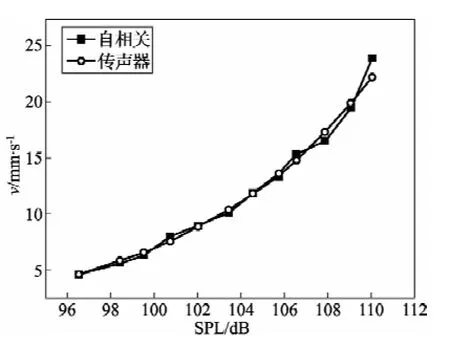
图7 频移为150 kHz两速度对比结果

通过两种不同频移信号处理结果得出，激光多普勒信号的自相关法适合于粒子振速较小时的测量，同时，用该方法测量粒子振速时，选择频移较大的信号有利于速度的精确测量，但高频信号也就意味着高的采样率，对数据采集和处理系统具有较高要求。

5 自相关信号的插值处理

根据式（6）得知，为了在较低的频移范围内获得更精确的结果，可以通过细化或“增大”周期数n的值以达到对速度值更精确的量化。本文采用了三次样条插值法对相关法周期数的估计，在已有的周期时间内4倍频率插值，与原始的自相关信号进行比较。在图4中，选取的是自相关信号各个周期的峰值点，周期间隔T＝1／Δf，Δf为频移，50 kHz。假设对信号单个周期内插入n个点，则插值后的信号频移也相应变化，即ΔF＝（n＋1）Δf。因此，在图8中，相关图的频移由原来的50 kHz变成200 kHz。

图8 频移为50 kHz相关图插值后的结果

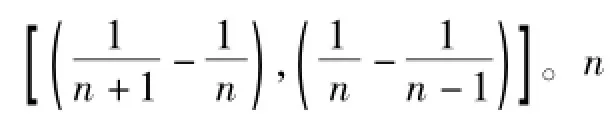
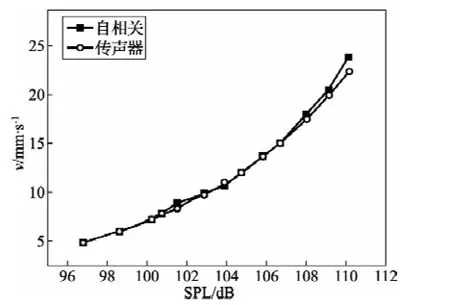
图9 插值后速度与传声器速度对比结果

6 结 论

本文通过光子自相关法对不同频移的多普勒信号处理的结果表明，自相关法测量声场中粒子振速与传声器测量声压值对应的粒子振速结果有着较好的一致性。同时，频移较高的信号更有利于获取高精度的速度量值，减少偏差。然而增大频偏量值，也就意味采样率和数据处理工作量的增加。为了在低频移的条件下获得准确的粒子振速，文中在自相关处理的基础上利用插值法实现了低频移信号对粒子振速量值的精确测量。激光多普勒测量声场中的粒子振速的研究与实现，将有利于推动光学法复现空气中声压量值的相关研究。

［1］ 沈熊.激光多普勒测速技术及应用［M］.北京：清华大学出版社，2004，1－7.

［2］ 张艳艳，巩轲，何淑芳，等.激光多普勒测速技术进展［J］.激光与红外，2010，40（11）：1157－1162.

［3］ Taylor K J.Absolute measurement of acoustic particle velocity［J］.JAcoust Soc Am，1976，59（3）：691－694.

［4］ Taylor K J.Absolute calibration ofmicrophonesby a laser Doppler technique［J］.J Acoust Soc Am，1981，70（4）：939－945.

［5］ Li Liang-jie，He Long-biao，Wang Xue-jing，et al.The Realization for Sound Pressure Unit Using Laser Doppler Anemometry in a Travelling Wave Tube［J］.Applied Mechanics and Materials，2013，239－240：57－64.

［6］ Greated C A.Measurement of acoustic velocity fields［J］.Strain，1986，22（1）：21－24.

［7］ MacGillivray T J，Campbell D M，Greated C A，et al. The development of a microphone calibration technique using Laser Doppler anemometry［J］.Acustica，2002，88（1）：135－141.

［8］ Sharpe JP，Greated C A.A stochastic model for photon correlationmeasurements in Sound fields［J］.Journal of Physics D：Applied Physics，1989，22（10）：1429－1433.

［9］ Koukoulas T，Theobalda P，et al.Towards a future primary method for microphone calibration：Optical measurement of acoustic velocity in low seeding conditions［J］.Optics and lasers in engineering，2008，46（11）：791－796.

［10］ Durrani T S，Greated C A.Laser systems in flow measurements［M］.New York：Plenum Press，1977，166.

Measurem ent of Partic le Vibration Velocity in Air-borne Sound Field w ith the Photon Correlation Method

LILiang-jie1， HE Long-biao2， WANG Xue-jing1
（1.College of Information＆Technology，Beijing University of Chemical Technology，Beijing 100029，China；
2.National Institute of Metrology，Beijing 100029，China；）

The particle vibration velocity is an important parameter to evaluate the characteristics of the sound field. Photoelectric signal of scatter light was obtained laser Doppler velocimetry at different sound pressure level in p lane wave sound field.And the Dopp ler signal was processed by autocorrelation method，the velocity can be calculated based on the time of characteristic values？？of the correlation function and comparedwith thatofmicrophone.Furthermore，on thebasis of the autocorrelation algorithm，the difference which caused by the ratio of the original signal frequency offset and the Doppler frequency is not an integer multiple was reduced by the interpolation method.The results demonstrate that the photon correlation method is able to obtain particle vibration velocity of the sound field.and results show good agreement with thatmeasured by microphone，interpolation method is conducive to decreasing the deviation when velocity is large relatively。The deviation of the twomethods is less than 0.7dB at the sound pressure level from 96 dB to 110 dB.

Metrology；Particle vibration velocity；Laser Doppler；Autocorrelation method；Interpolationmethod

TB95

A

1000-1158（2014）04-0363-05

10．3969／j．issn．1000-1158．2014．04．13

2013-03-11；

2013-05-23

李良杰（1987－），男，福建宁德人，北京化工大学硕士研究生，主要从事激光测量技术的研究。gutian2755＠126.com何龙标为本文通讯作者。helb＠nim.ac.cn