基于局部均值分解和极值延拓的旋转机械故障特征提取方法

孟 宗， 王亚超， 王晓燕

（燕山大学河北省测试计量技术及仪器重点实验室，河北秦皇岛 066004）

基于局部均值分解和极值延拓的旋转机械故障特征提取方法

孟 宗， 王亚超， 王晓燕

（燕山大学河北省测试计量技术及仪器重点实验室，河北秦皇岛 066004）

局部均值分解对非平稳、非线性故障信号进行平稳化处理时表现出特有的分析能力，能够有效获得故障信号的时频特征，然而局部均值分解过程中存在的端点效应严重影响信号的分解效果。针对这一问题，提出了一种基于局部均值分解和极值延拓的旋转机械故障提取方法。首先采用极值延拓方法处理信号的两个端点，左、右端点均分别延拓2个极大值和2个极小值，然后对延拓后的信号进行局部均值分解，提取信号中包含的故障特征。仿真结果表明，经过极值点延拓后，局部均值分解过程中的端点效应得到了有效抑制，最后以轴承内圈故障为例在实验平台进行了实验研究，实验结果表明，该方法能有效提取出旋转机械故障特征。

计量学；局部均值分解；端点效应；旋转机械

1 引 言

旋转机械是应用非常广泛的一类机械设备，随着现代工业和科学技术的飞速发展，旋转机械设备日益朝着高速化、自动化、超临界化和大功率、大载荷等方向发展，其工况不仅影响该机械设备本身的安全运行，而且还会对后续生产和运行造成直接影响，因此，对其运行状况进行实时监测和故障诊断越来越受到人们的关注。旋转机械发生故障的主要特征是机器伴有异常的振动和噪声，其振动信号实时地反映了机械设备的故障信息。旋转机械设备运行时，特别是在出现故障的情况下，其振动信号具有明显的非线性非平稳特性［1～3］，然而传统的故障特征提取方法通常是建立在信号的平稳性假设基础上，无法同时兼顾非平稳信号在时域和频域的全貌和局部化特征。近年来，时频分析方法作为分析时变非平稳信号的有力工具，成为现代信号处理方法研究的热点，典型的时频分析方法有短时傅里叶分析、小波变换、Wigner-Ville分布、经验模态分解等［4～6］。Smith JS在2005年提出了一种新的自适应非平稳信号的分析方法——局部均值分解（Local Mean Decomposition，LMD）方法［7］，由于旋转机械工程领域存在大量的非平稳信号，而这些非平稳信号大多是调制信号，解调是一种有效的分析方法，采用LMD方法对机械故障振动信号进行分解，提取各个分量的瞬时幅值和瞬时频率，能够得到信号完整的时频分布，从而可以有效地提取出振动信号的特征。目前，LMD方法已在生物医学［7］和机械故障诊断［8～10］等领域迅速得到应用。但LMD仍然存在端点效应，影响分解效果，本文提出了基于极值点延拓的LMD端点效应抑制方法，并成功应用于旋转机械故障特征提取中。

2 局部均值分解原理

局部均值分解方法可将一个复杂的非平稳信号自适应地分解成多个瞬时频率具有物理意义的乘积函数（production function，PF）xPF（t），每一个xPF（t）分量均是由一个纯调频信号和一个包络信号相乘得到的，其中包络信号是该xPF（t）分量的瞬时幅值，该xPF（t）分量的瞬时频率可以由调频信号直接求出，将所有xPF（t）分量的瞬时幅值和瞬时频率组合即可得到原始信号完整的时频分布，从而能够清晰准确地反映出信号能量在空间各尺度上的分布规律。对于信号x（t），LMD的分解过程如下：

（1）找出原始信号x（t）所有的局部极值点ni，求出所有相邻的局部极值点的平均值

用直线把所有相邻的平均值点mi连接起来，然后再用滑动平均法对它进行平滑处理，可以得到局部均值函数m11（t）。

（2）求包络估计值

用直线把所有相邻2个包络估计值ai连接起来，然后采用滑动平均方法对它进行平滑处理，可以得到包络估计函数a11（t）。

（3）从原始信号x（t）中分离出局部均值函数m11（t），可得

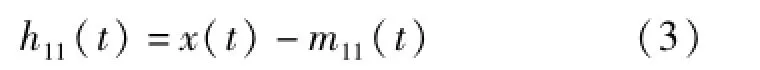
（4）用h11（t）除以包络估计函数a11（t），对h11（t）进行解调，可得

2.5.3除草视田间杂草危害情况人工除草3～6次，去除的杂草可填埋在钩藤植株根部，或带出种植地块统一堆放。

将s11（t）作为原始信号回到步骤（1）重复（1）～（4），得到s11（t）的包络估计函数a12（t）。如果a12（t）不等于1，继续将s12（t）作为原始信号回到步骤（1）重复（1）～（4），重复上述迭代过程n次，直到s1n（t）的包络估计函数a1（n＋1）（t）＝1，即s1n（t）为一个纯调频信号，停止迭代，得到

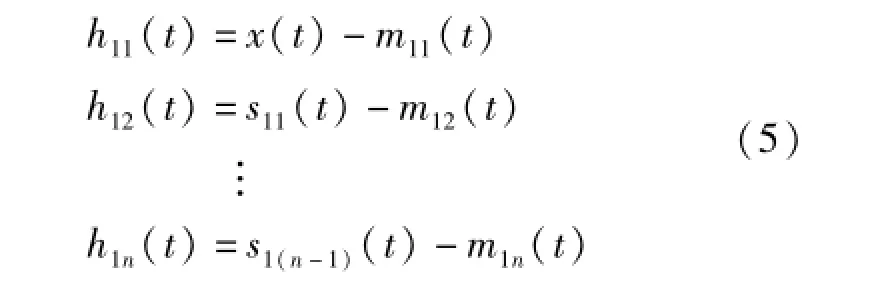
式中，s11（t）＝h11（t）／a11（t）；s12（t）＝h12（t）／a12（t）；…；s1n（t）＝h1n（t）／a1n（t）。

（5）将迭代过程中产生的所有包络估计函数相乘便可以得到包络信号（瞬时幅值函数）

将包络信号纯调频信号s1n（t）乘以a1（t），便可以得到原始信号x（t）的第一个xPF（t）分量

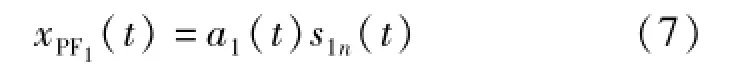
原始信号中最高的频率成分均包含在了该分量中，该分量是一个单分量的调幅-调频信号，它的瞬时幅值就是包络信号a1（t），它的瞬时频率f1（t）则可以通过纯调频信号s1n（t）求出，即

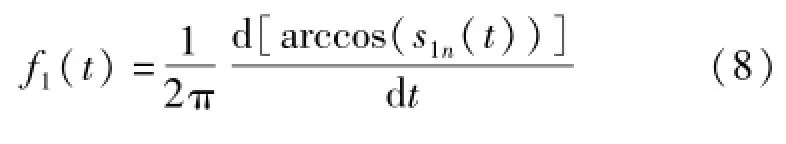
（6）将第一个分量xPF1（t）从原始信号x（t）中分离出来，得到一个新的信号u1（t），将u1（t）作为原始信号回到步骤（1）重复以上步骤，从而得到第二个分量xPF2（t），依次类推，循环k次，直到uk为一个单调函数为止。从而得到

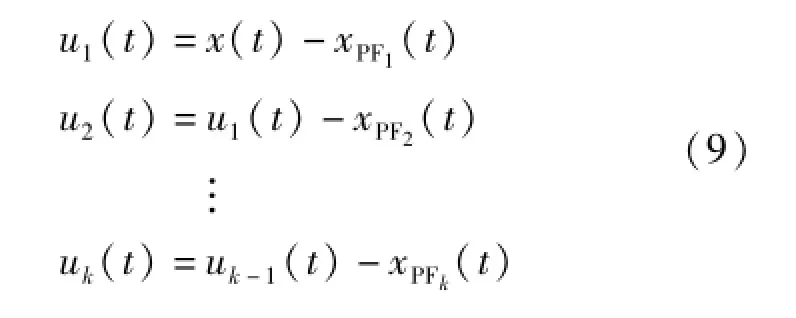
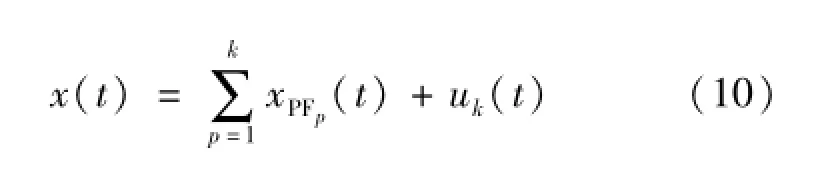
3 极值点延拓方法研究

实际中存在的信号序列，长度往往是有限的，在无法已知端点以外的信号的情况下，只能根据己知信号推测其端点附近的包络估计函数和局域均值函数，从而不可避免地会产生误差，因此，LMD受到端点效应的影响。本文提出采用极值延拓方法对信号的两个端点进行处理，从而达到抑制LMD端点效应的目的。

设离散信号

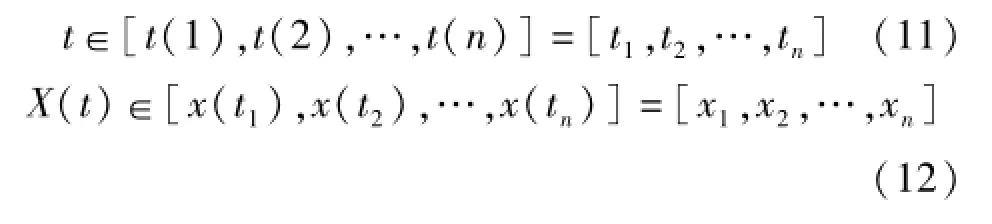
采样步长为X（t），有M个极大值和N个极小值，它们对应的序列下标为（Im，In）、时间（Tm，Tn）和函数（U，V），记为

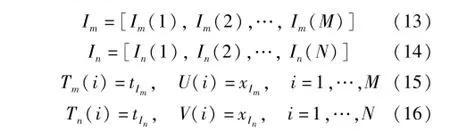
在分解时，极值点延拓的目的是保证上、下包络均能和端点相交，以便有与每一个信号点相对应的局部平均值。而上、下包络是由极大值和极小值连结而成的，因此不必对信号本身进行延拓，而只要对极大值和极小值进行延拓。极大值和极小值是相间分布的，另外考虑到样条插值的要求，所以只要在信号的左、右两端采用极值点延拓法，分别延拓2个极大值和2个极小值。

（1）左端

信号左端第一个特征波包含的信号点数k1

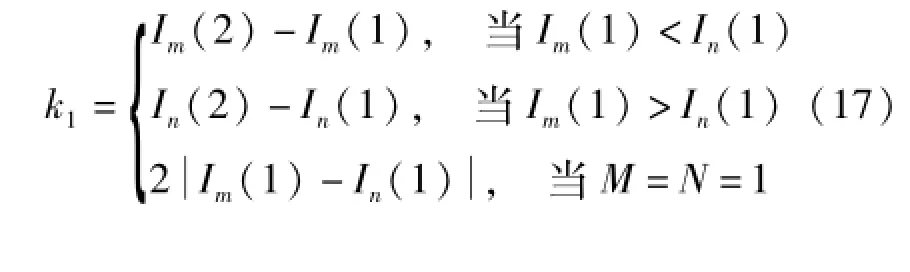
左延拓的2个极值的位置（Tm，Tn）和数值（U，V）为

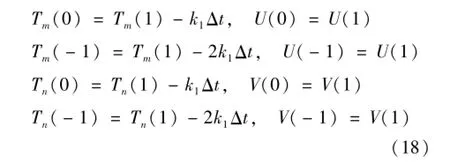
（2）右端

信号右端第一个特征波包含的信号点数k2

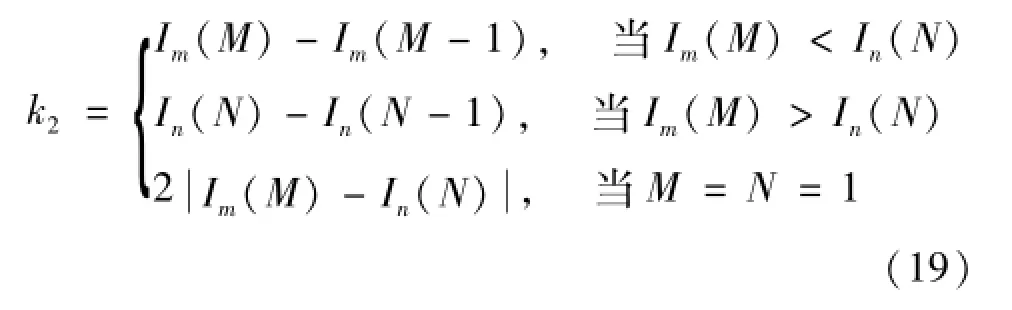
右延拓的2个极值的位置（Tm，Tn）和数值（U，V）为

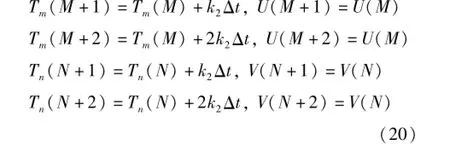
当端点的数值比近端点的第一个极大值大或比近端点的第一个极小值小时，进行如下特殊的处理，以避免信号落到包络线之外，然后用滑动平均值方法求曲线的上、下包络线。

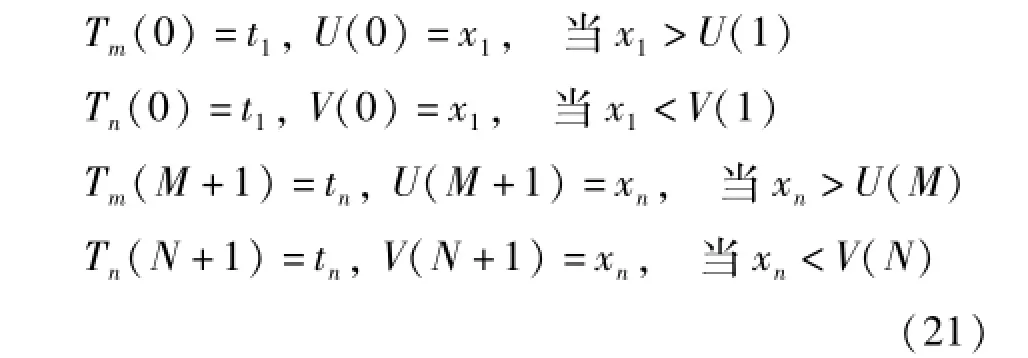
4 仿真研究

为了验证极值点延拓方法抑制LMD端点效应的有效性，建立非平稳信号x（t）

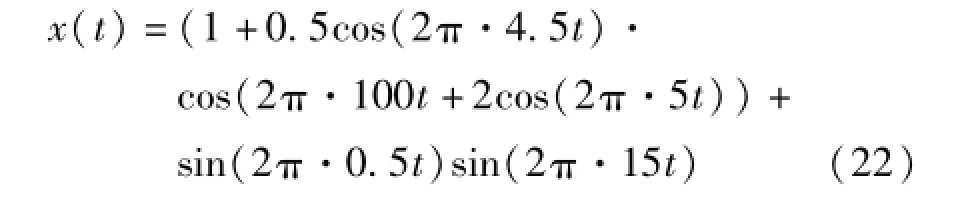
其时域波形见图1，采用LMD对其进行分解，迭代终止条件为1－Δ≤a1n（t）≤1＋Δ，其中Δ＝0.001。

首先，不进行端点处理，直接对图1信号进行局部均值分解，得到的分解结果见图2。然后，采用极值延拓法分别对左、右端点进行极值点延拓处理后，再进行局部均值分解得到分解结果见图3。对比图2和图3可以明显看出，没有经过端点处理时，xPF（t）分量在端点处幅度变化较大，其失真程度较明显，xPF2（t）及残余项R端点处波动较大，经过极值点延拓法处理后，对应xPF（t）分量的瞬时幅值和瞬时频率端点处波动较小，较好地反映了仿真信号的幅值和频率特征。仿真结果表明，采用极值点延拓法，端点效应得到了较好地抑制，局部均值分解获得的各个xPF（t）分量的瞬时幅值和瞬时频率反应了原始信号的真实信息。

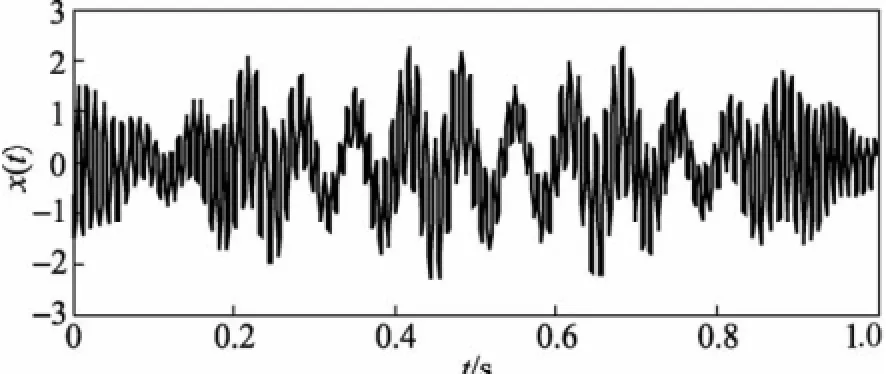
图1 仿真信号x（t）的时域波形

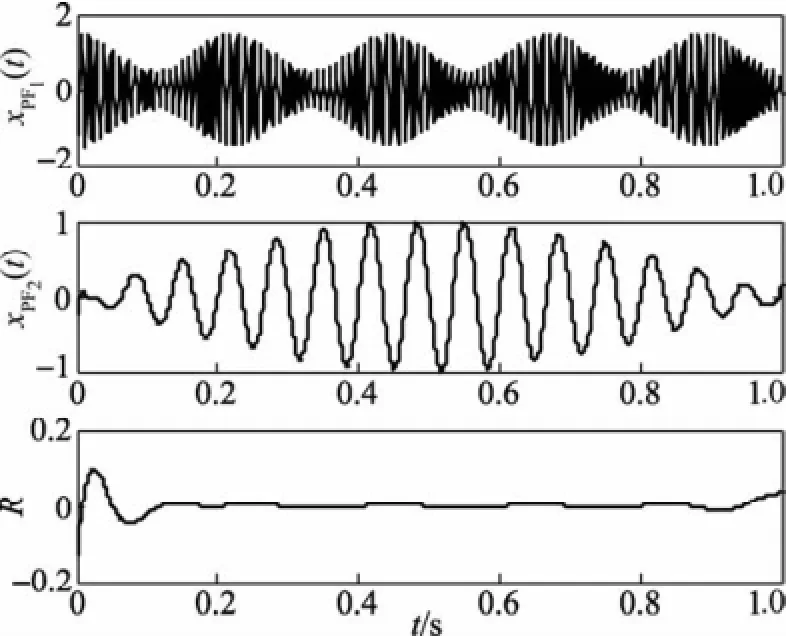
图2 未经过端点处理时信号x（t）的分解结果

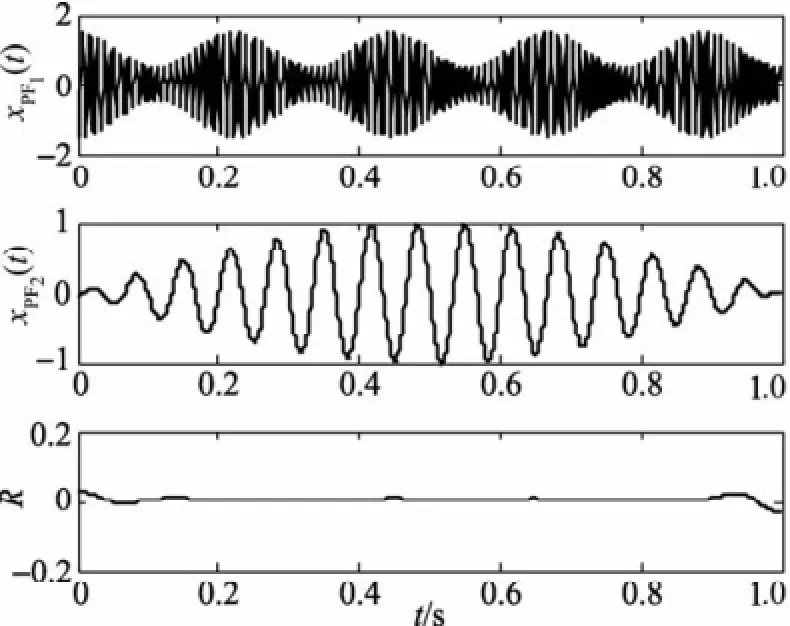
图3 解决端点效应后信号x（t）的分解结果

5 实验研究

为了验证本文方法在机械故障特征提取领域的可行性和有效性，在轴承故障试验台进行了实验研究。试验台转子转速为1797 r／min，轴承故障为内圈单点电蚀故障，故障尺寸为1.18μm，采样频率为12000Hz，轴承内圈故障特征频率为162.08 Hz，转轴基频为29.95Hz。采集一组轴承内圈故障振动信号见图4，由图可以看出故障信号出现周期性冲击成分。利用LMD对轴承内圈损伤时所采取的数据进行分解，分解结果见图5。

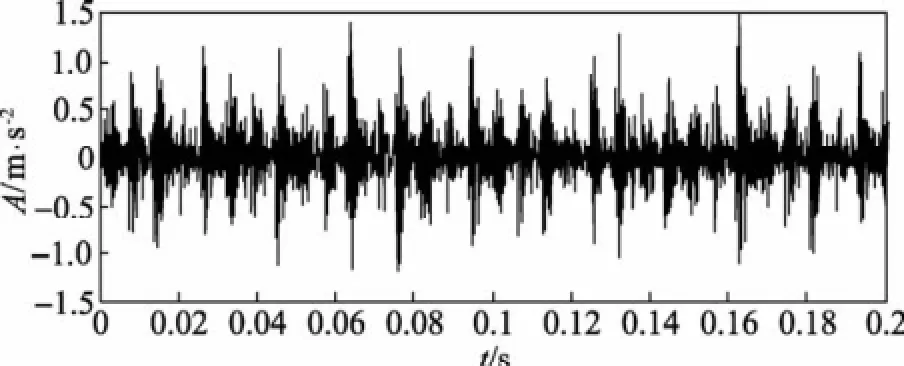
图4 轴承内圈信号的时域波形

图5 轴承内圈故障信号的LMD分解结果

图6到图9分别为xPF1（t）～xPF4（t）分量所对应的包络频谱图。由于xPF5（t）分量对应的包络频谱图的幅值相对较小，可以不考虑。由图6可以看出，在161.1Hz及其2倍频322.3Hz处有明显的峰值，这与轴承内圈故障频率162.08 Hz及其2倍频非常接近，在58.59 Hz处也有峰值，这与转轴基频的2倍频59.90Hz非常接近，此外，由于转轴频率的调制作用，在fi－2f处即102.2Hz附近也出现了峰值；在图7中，同样在161.08 Hz和59.90 Hz附近出现了频率峰值；图8中，162.1 Hz附近有峰值外，出现了29.3Hz的频率峰值，这与转轴基频29.95 Hz非常接近；图9也在29.3 Hz附近有明显的峰值。综上分析可以判断轴承内圈出现了以162.08Hz为特征频率的内圈故障。验证了该方法的有效性和可行性。

图6xPF1（t）分量对应的功率谱图

图7xPF2（t）分量对应的功率谱图

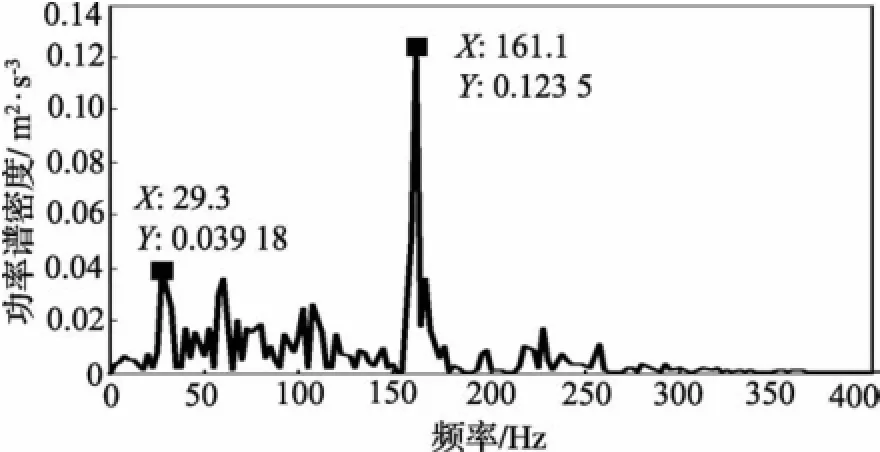
图8xPF3（t）分量对应的功率谱图

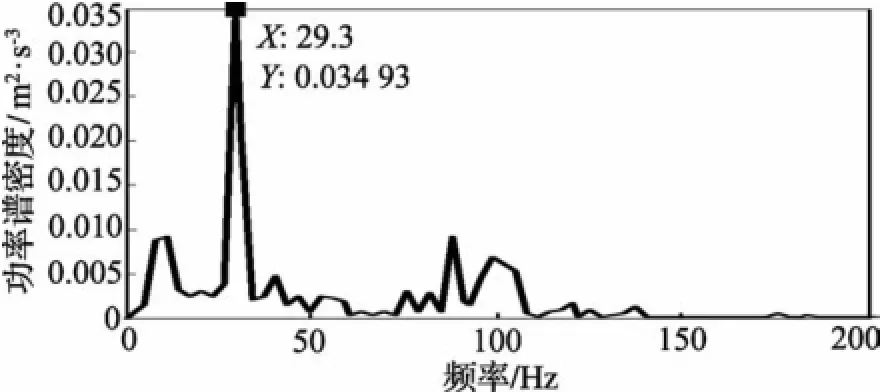
图9xPF4（t）分量对应的功率谱图

6 结 论

本文提出了一种基于局部均值分解和极值延拓的旋转机械故障提取方法。利用局部均值分解方法对非平稳、非线性信号进行平稳化处理时表现出特有的分析能力，有效获得非平稳信号的时频特征。同时针对局部均值分解方法存在的端点效应问题，提出了基于极值点延拓的端点效应处理方法，仿真结果表明，该方法有效地抑制了局部均值分解过程中的端点效应。最后在实验平台以轴承内圈故障为例进行了实验研究，实验结果表明，基于局部均值分解和极值延拓的方法能有效提取出旋转机械故障特征。

［1］ 刘小峰，秦树人，柏林.基于小波包的经验模态分解法的研究及应用［J］.中国机械工程，2007，18（10）：1201－1204.

［2］ 罗跃纲.旋转机械故障的非线性问题及智能诊断技术［M］.北京：科学出版社，2009

［3］ 褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法［M］.北京：科学出版社，2009.

［4］ 李志农，何永勇，褚福磊.基于Wigner-Ville高阶谱的机械故障诊断的研究［J］.机械工程学报，2005，41（4）：119－122.

［5］ 谢平，王欢，杜义浩.基于EMD和Wigner-Ville分布的机械故障诊断方法研究［J］.计量学报，2010，31（5）：390－394.

［6］ 孟宗，顾海燕，刘利晖，等.基于EMD与AR谱的轧机主传动系统故障诊断研究［J］.计量学报，2011，32（4）：338－342.

［7］ Sm ith J S.The local mean decomposition and its application to EEG perception data［J］.Journalofthe RoyalSocietyInterface，2005，2（5）：443－454.

［8］ Yang Y，Cheng JS，Zhang K.An ensemble localmeans decomposition method and its application to local rubimpact fault diagnosis of the rotor systems［J］.Measurement，2012，45（3）：561－570.

［9］ 鞠萍华，秦树人，赵玲.基于LMD的能量算子解调方法及其在故障特征信号提取中的应用［J］.振动与冲击，2011，30（2）：1－4.

［10］ 程军圣，杨宇，于德介.局部均值分解方法及其在齿轮故障诊断中的应用［J］.振动工程学报，2009，22（1）：76－83.

Rotating Machinery Fault Diagnosis Method Based on
the LocalMean Decom position and Extreme Points Extension

MENG Zong， WANG Ya-chao， WANG Xiao-yan
（Key Laboratory of Measurement Technology and Instrumentation of Hebei Province，Yanshan University，Qinhuangdao，Hebei066004，China）

Local mean decomposition shows unique analysis ability when smoothing process the nonstationary，nonlinear fault signal.It can effectively obtain time-frequency characteristics of fault signal.However，the end effect existing in the process of the localmean decomposition seriously affects the signal decomposition result.In order to solve this problem，amethod of rotating machinery fault extraction based on the local mean decomposition and extreme points extension is proposed.Firstly，using themethod of extreme points extension to process the two endpoints of the signal.The left and right endpoints are respectively extended twomaximums and twominimums.Then，using themethod of localmean decomposition to decompose the signal with extension，and extract fault features it contains.The simulation results show that，after extreme points extension，the end effect in the process of local mean decomposition have been effectively suppressed.Finally，with the bearing inner race fault as an example experimental study was carried out in experimental platform.The experimental results show that this method can effectively extract the fault characteristics of rotating machinery.

Metrology；Localmean decomposition；End effect；Rotatingmachinery

TB936

A

1000-1158（2014）05-0469-05

10．3969／j．issn．1000-1158．2014．05．13

2012-12-29；

2013-03-29

国家自然科学基金（51105323）

孟宗（1977－），男，河北保定人，燕山大学副教授，博士、主要研究方向为信号分析与处理、旋转机械故障诊断。mzysu＠ysu.edu.cn