基于各向异性理论的深水区地震资料叠前处理技术

张振波，轩义华，刘 宾

中海石油（中国）有限公司深圳分公司，广东 深圳 518067

0 引言

白云6-1构造位于南海北部深水白云凹陷西南，具有复杂特殊的地质条件。它位于洋陆过渡地壳的白云凹陷，具有边缘海独特的地球动力环境，沉积环境由陆相逐渐演变为浅海、陆坡深水环境，发育了巨厚的深水沉积，因此白云深水区具有形成大型油气区的地质基础。越来越多的野外实践都强有力地证实［1－3］，地壳中存在着各向异性，在深水区地震资料中多次波干扰非常发育［4］，这些现象严重制约了地震波场成像的精度。具有垂向对称轴的横向各向同性（VTI）介质是一种最简单、最普遍的各向异性介质，其广泛存在于水平成层的页岩中。此外，周期性薄层在宏观尺度上也体现出横向各向同性。在均匀VTI介质中，地震波沿水平方向传播时体现了横向各向同性，沿其他方向传播时则体现各向异性，即速度与方向有关［5］。并且随着各向异性程度的增加，地震波的振幅和走时与各向异性介质中的相比有很大的差别。Thomsen引入了各向异性参数，描述VTI介质各向异性的程度变得更加简单和直观。白云6-1构造因为特殊岩性（火成岩和碳酸盐岩）的存在，各向异性现象广泛存在。为了更好地提高该深水区地震资料成像质量，笔者在研究区引入基于VTI介质叠前地震资料处理技术系列，提高了地震资料的信噪比，成像结果更加可靠。

1 VTI介质波动理论与成像原理

1.1 VTI介质

各向异性的形式与其成因一样是复杂的，但对沉积型地层，其基本模式主要为VTI模式［6］。它用来描述沉积盆地地层的微细层理和旋回性薄层引起的各向异性，属六方晶系，其对称轴是垂直的，在垂直于一个轴的方向上具有相同的弹性特征；但在平行于该轴的方向上弹性特征却不同（图1）。Postman［7］指出：由各向同性岩石的周期性薄层所构成的地下岩石，由于波长远大于地层的厚度，可等价于具有垂向对称轴的横向各向同性固体，因此该模式有大的广泛应用性。

VTI介质模型对应的弹性系数矩阵可表示

为［8-9］

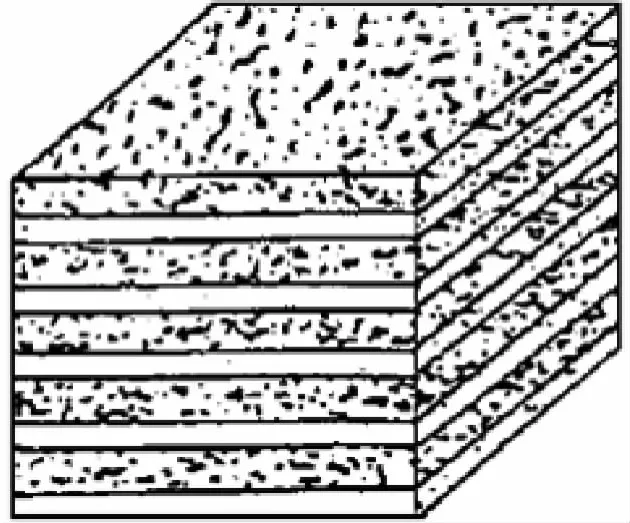
图1 VTI介质模型Fig.1 VTI media model

公式（1）表明，VTI介质的弹性系数矩阵中有5个独立 的 弹 性 参 数：c11，c13，c33，c44，c66，其 中，c12＝c11－2c66。采用Thomsen各向异性介质参数描述方法，可以把描述P波运动学特征的独立参数减少到3个［10－11］。VTI介质的弹性系数可以变换为Thomsen参数：

式中：ρ为介质密度；vP0、vS0分别为qP波和qS波的垂直方向传播速度；ε、γ、δ均为与介质各向异性有关的Thomsen参数，ε表征纵波各向异性程度，γ表征横波各向异性程度，δ为变异系数。

1.2 VTI介质中的波动方程

对于 VTI介质，只有c11，c13，c33，c44，c66这5个独立的弹性系数。对一般性各向异性介质，其弹性波动方程可表示为

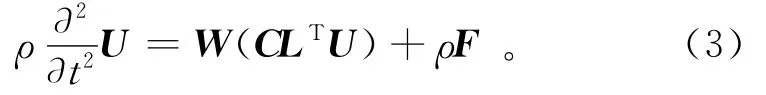
式中：U为弹性波场矢量；W为微分算子；C为弹性系数张量矩阵；F为外力矢量。

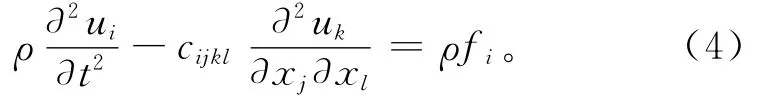
式中：ui，uk（i，k＝1，2，3）为波场在3个坐标方向的分量；t为时间；cijkl（i，j，k，l＝1，2，3）为张量系数；x′j，xl（j，l＝1，2，3）为空间坐标；fi（i＝1，2，3）为外力分量。根据应力张量的对称性，张量系数可由81个减少到36个。而对于VTI介质，弹性张量简化为式（1）。

在二维介质中，设fi＝0，用式（1）对式（4）简化，即可得二维横向各向同性介质中的弹性波动方程：

或以张量下标方法表示为

上述方程组可分解为一个独立的波动方程（6）及一个波动方程组（5）和（7）。方程（6）是横向各向同性SH波波动方程；方程组（5）和（7）则是准P波和SV波波动方程，它们是耦合在一起的，即在VTI介质中，P波传播可引起SV波，SV波传播也可引起P波。

1.3 VTI介质最小平方偏移

各向异性介质地震波场偏移通常采用Kirchhoff积分法，笔者则采用了最小平方Kirchhoff偏移。对于海上地震采集，正演过程可以表示成

其中：d为地震记录；L是正演线性算子，包括所有传播项（贯穿速度模型的格林函数）；m为反射系数矩阵。

将成像视为最小二乘意义下的反演问题，即最小二乘偏移［12］。最小二乘偏移能改善偏移结果，压制偏移人工痕迹。定义如下目标函数：

式中：r是正则化参数；mapr为先验模型。等式右边第一项为数据的误差函数项；第二项为正则化项。

可以通过梯度优化法，比如最速下降法、共轭梯度法在模型空间求取目标函数最小值以估计实际地下反射系数。共轭梯度迭代格式为

式中：n为迭代次数；α为迭代步长；β为Fletcher和Reeves参数；p为搜索方向；g为梯度。

最小平方偏移算法压制了偏移噪声，平衡了振幅，提高了成像分辨率。它适合于所有的偏移方法，即Kirchhoff偏移、单程波动方程偏移或者逆时偏移。

2 深水地震资料各向异性叠前处理技术

2.1 多次波衰减技术

白云地区海底崎岖，深海环境中的复杂构造及其严重的侧面反射和各向异性特质等使得该工区三维资料处理存在诸多难点。海底多次波和层间多次波发育，常规的地表多次波预测技术难以奏效。笔者采用适用于复杂海底构造多次波压制的三维广义多次波预测技术（general surface multiple prediction，GSMP），选择有效的压制多次波方法组合，在最大限度保护有效信息的前提下，消除多次波、突出有效波。3DGSMP技术采用三维数据计算多次波模型，弥补了采用单一采集方向数据进行多次波预测的缺陷，特别适合应用于崎岖海底、构造复杂的地区。二维方法预测的多次波反射点范围只能在单方位角内，而GSMP是在三维范围的孔径，能够准确地预测侧面反射的多次波（图2）。

在海底崎岖复杂情况下，通过共偏移距道集中建立的多次波模型（图3）可以看到，采用常规的2D SRME的多次波压制技术处理时，预测的时间和形态（图3b）与实际数据（图3a）有着较大的差异，说明没有达到去除多次波的目的；而3DGSMP较为准确地建立了多次波模型（图3c），形态和时间都与实际数据（图3a）比较匹配，对深水复杂构造地区的多次波进行了有效压制。

从2DSRME和3DGSMP去除多次波相邻两炮炮集结果对比（图4）来看，3DGSMP（图4c）较输入炮集（图4a）和2DSRME（图4b）能更有效地去除多次波能量、保留有效波能量。

图2 复杂构造下的多次波反射路径Fig.2 Multiple reflection path for complex structure

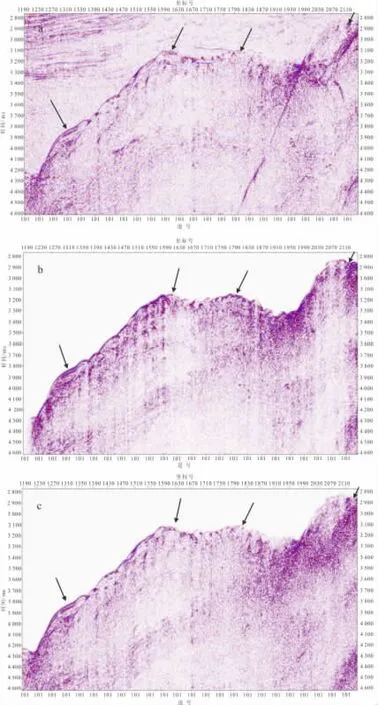
图3 共偏移距道集中建立的多次波模型对比Fig.3 Contrast of the multiple wave models built from common offset gather

图4 2DSRME和3DGSMP去除多次波炮集结果对比Fig.4 Contrast of shot gathers after 2DSRME and 3D GSMP

2.2 各向异性速度分析

本文采用的最小平方Kirchhoff方法是利用波动方程的Kirchhoff积分进行波场外推，并在Kirchhoff积分偏移的基础上结合射线理论进行偏移速度分析，同样，速度模型的建立是各向异性介质地震波场精确偏移的基础。由Alkhalifah等［13－19］研究发现，在纵波的时间域处理中可以用等效各向异性参数反映近偏移距地震波速度，VTI介质的非双曲线时距方程为

式中：t0为自激自收时间；vnmo为动校正速度；η为非椭圆各向异性参数；vP0为与对称轴垂直方向的纵波速度；ε、δ为Thomsen各向异性参数；vhor为水平速度。

速度分析工作建立在速度拾取基础上，分别在不同的处理阶段共进行了四轮速度拾取（图5）。速度分析共分2个阶段：1）第一阶段由井数据和初始速度分析组成。井数据分析得到的速度用于最开始的几何扩散补偿。在第一次进行初始速度速度分析时，以井数据分析得到的结果作为参考速度并对全工区范围进行500m×500m网格的速度拾取。初始速度主要是为地震数据偏移归位前的Radon算法去多次波工作和目标线的偏移归位工作提供速度。2）第二阶段由各向异性速度分析、剩余速度分析和高密度叠加速度分析组成。在拾取了各向同性速度的基础上拾取δ场，得到各向异性速度场，网格是500m×500m。层状地层的水平速度通常比垂向速度快2%～15%，因此如果射线近垂向传播，那么各向异性可以忽略不计，但是对于弯曲射线理论下的宽角度射线路径，不考虑各向异性不能反映地下真实速度。

图5 速度分析的流程Fig.5 Workflow of velocity analysis

由于本区工区浅层地质构造复杂，所以我们拾取δ场各向异性参数的策略如下：

1）先人工拾取稀疏的δ得到初始变异系数；

2）然后通过初始变异系数插值得到全部速度分析点上加密的变异系数；

3）调整加密后变异系数中的异常值，将其作为模型，反演得到用于各向异性偏移测试的变异系数；

4）在反演得到的变异系数基础上扩展变异系数场到5s附近，同样通过自动反演，得到反演修正后的变异系数；

5）将反演修正后的变异系数平滑后，再进行检查，作为最终的各向异性场，得到各向异性速度。

图6显示的是拾取各向异性速度的4个主要窗口，分别是速度谱、δ值、各向同性速度动校正结果和各向异性动校正结果。可以明显看到，在各向异性属性应用之后，大部分的同相轴在远偏移距拉平效果更佳。所以在时间偏移射线旅行时计算假设的情况下，虽然从图6中可以看到反射轴有部分没有拉平的现象，但总体来说因为引入了各向异性参数还是有利于远道集的拉平。在拾取完δ场之后，就得到全区的各向异性速度。

通过速度分析建立相对精确的偏移速度场，并且通过对远偏移距分析求取各向异性参数。由于本地区海底之下的地质构造形态复杂，常规速度分析不能够满足精确的叠加需求；因此，笔者采用了部分道集的平移初至走时双参数反演的方法进行了试验研究。最后采用高密度速度分析对工区速度形态进行了细致地描述，为后续工作提供了良好的速度模型。

图7为高密度速度分析得到的速度剖面主测线和联络测线显示图。从图7可以看出，应用了δ各向异性分析的速度场深部能量聚焦，高密度分析后的层速度描述了细节的地质信息。图8为主测线分别应用各向同性和各向异性分析之后得到的地震叠加剖面对比图。从图8可以看出，应用了各向异性分析的地震叠加剖面反映出来的断层断面更加清晰，有助于后续解释工作的进行。

图6 各向异性速度分析Fig.6 Anisotropic velocity analysis

图7 高密度速度分析得到的主测线（a）和联络测线（b）速度剖面Fig.7 High-density velocity analysis sections of inline（a）and xline（b）

图8 主测线深部各向同性（a）及各向异性（b）叠加结果分析对比Fig.8 Contrast of the stacking sections with isotropic（a）and anisotropic（b）velocity analysis

2.3 各向异性叠前时间偏移处理

在本次研究中叠前时间偏移主要采用基于Kirchhoff积分公式的积分类方法。偏移半径为6 000m，偏移距组为49组，反假频因子为18.75m×37.5m。

图9和图10分别是应用了各向异性前后主测线和联络测线的地震叠加剖面。从引入了δ分析的地震叠加剖面来看（图9b、图10b），断层能量较各向同性分析得到的地震叠加剖面 （图9a、图10a）能更好地聚焦。虽然δ值不大，但是大大提高了地震资料的成像质量，有效保证了振幅和相位的真实性。剖面中多次波的压制更彻底，更好地保留了地震数据中的有效信息。

图9 主测线地震数据增益叠加剖面对比Fig.9 Contrast of the inline stacking sections with seismic data gain

图10 联络测线地震数据增益叠加剖面对比Fig.10 Contrast of the xline stacking sections with seismic data gain

3 结论

基于各向异性机制的地震资料处理较基于各向同性机制的地震资料处理方法是客观和严谨的。通过基于VTI介质叠前地震资料处理技术系列在南海深水白云6-1构造的应用认为：该技术系列中3D GSMP技术较适用于白云6-1这种深水环境且海底崎岖的复杂工区；GSMP建立的多次波模型，形态和时间都比较匹配，能对多次波进行较有效地压制、地震剖面效果显著；基于各向异性的高密度速度分析的层速度较好地描述了细节地质信息，断裂断层构造在速度上也有一定速度变化与其对应，偏移后道集的信噪比有所提高，并在远偏移距拉平效果较好；基于各向异性叠前时间偏移处理结果剖面的断层能量得到进一步聚焦，地震资料成像质量得到提高。该技术系列有助于南海东部海域复杂工区的勘探工作，可以进一步推广应用。

（

）：

［1］安德森 D L.地球的理论［M］.关华平，杨玉荣，刘小伟，等，译.北京：地震出版社，1993.

Anderson D L.Theory of the Earth［M］.Translated by Guan Huaping，Yang Yurong，Liu Xiaowei，et al.Beijing：Seismological Publishing House，1993.

［2］Crampin S.Effective Elastic Constants for Wave Propa-gation in Cracked Solids［J］.Geophysics，1984，76：135-145.

［3］Alford R M.Shear Data in the Pre-sence of Azimuthal Anisotropy ［C］//The 56th SEG Annual Meeting Expanded Abstracts.Houston：［s.n.］，1986：476-479.

［4］石颖，刘洪，历玉英.逆数据域表面多次波压制方法［J］.吉林大学学报：地球科学版，2011，41（1）：271-277.

Shi Ying，Liu Hong，Li Yuying.Surface Related Multiple Attentiuation Method Investigation in Inverse Domain［J］.Journal of Jilin University：Earth Science Edition，2011，41（1）：271-277.

［5］韩颜颜，郭智奇，刘财，等.弹性各向异性介质速度特征分析［J］.吉林大学学报：地球科学版，2008，38（增刊1）：80-84.

Han Yanyan，Guo Zhiqi，Liu Cai，et al.The Analyse of Velocity Feature of Elastic Anisotropic Media［J］.Journal of Jilin University：Earth Science Edition，2008，38（Sup.1）：80-84.

［6］张中杰.地震各向异性研究进展［J］.地球物理学进展，2002，17（2）：281-293.

Zhang Zhongjie.A Review of the Seismic Anisotropy and Its Applications［J］.Progress in Geophysics，2002，17（2）：281-293.

［7］Postman G W.Wave Propagation in a Stratified［J］.Geophysics，1955，20：780-906.

［8］何樵登，张中杰.横向各向同性介质中地震波及其数值模拟［M］.长春：吉林大学出版社，1996.

He Qiaodeng，Zhang Zhongjie.Seismic Wave and Its Numerical Modeling in Transversally Isotropic Medium［M］.Changchun：Jilin University Press，1996.

［9］何樵登.地震勘探原理和方法［M］.北京：地质出版社，1986.

He Qiaodeng.Seismic Exploration Theory［M］.Beijing：Geological Publishing House，1986.

［10］Daley，Hron.Reflection and Transmission Coefficients for Transversely Isotropic Media［J］.Bull Seis Soc Am，1977，67：661-675.

［11］Thomsen L.Weak Elastic Anisotropy［J］.Geophysics，1986，51：1954-1966.

［12］Nemeth T，Wu C，Schuster G T.Least Squares Migration of Incomplete Reflection Data ［J］.Geophysics，1999，64（1）：208-221.

［13］Alkhalifah T.An Acoustic Wave Equation for Anisotropic Media［J］.Geophysics，2000，65：1239-1250.

［14］Alkhalifah T.Acoustic Approximations for Processing in Transversely Isotropic Media ［J］.Geophysics，1998，63：623-631.

［15］Alkhalifah T，Tsvankin I.Velocity Analysis in Transversely Isotropic Media［J］.Geophysics，1995，60（5）：1550-1566.

［16］Grechka V，Tsvankin I.3DDescription of Normal Moveout in Anisotropic Inhomogeneous Media［J］.Geophysics，1998，63（4）：1079-1092.

［17］Tsvankin I.Seismic Signatures and Analysis of Reflection Data in Anisotropic Media［J］.Elsevier Science，2005.

［18］张博.VTI介质高精度动校正和速度分析技术研究［D］.长春：吉林大学，2012.

Zhang Bo.Study on High Precision NMO and Velocity Analysis［D］.Changchun：Jilin university，2012.

［19］田建章，陈会敏，曹建华，等.各向异性处理技术探索与实践［J］.石油天然气学报，2010，32（3）：255-258.

Tian Jianzhang，Chen Huimin，Cao Jianhua，et al.Exploration and Practice of Anisotropic Treating Techniques［J］.Journal of Oil and Gas Technology，2010，32（3）：255-258.