不同掺合料掺量的活性粉末混凝土抗压强度试验
2014-06-07金凌志李月霞
金凌志,李月霞,付 强
(桂林理工大学a.广西矿冶与环境科学实验中心;b.广西岩土力学与工程重点实验室,广西 桂林 541004)
不同掺合料掺量的活性粉末混凝土抗压强度试验
金凌志a,李月霞b,付 强b
(桂林理工大学a.广西矿冶与环境科学实验中心;b.广西岩土力学与工程重点实验室,广西 桂林 541004)
通过活性粉末混凝土试件的受压试验,研究不同掺合料掺量的活性粉末混凝土在标准养护28 d条件下的受压力学性能。分析活性粉末混凝土立方体抗压强度、棱柱体抗压强度、弹性模量和峰值应变的相互换算关系,拟合出活性粉末混凝土应力-应变曲线方程式。研究结果表明:掺合料含量对活性粉末混凝土抗压强度影响较大,不同掺合料对活性粉末混凝土强度影响由大到小依次为:粉煤灰>硅粉>双掺粉煤灰和石英粉>硅微粉>石英粉,当粉煤灰掺合料掺量为40%时,活性粉末混凝土能达到较高强度。
活性粉末混凝土;不同掺合料;强度;应力-应变曲线
0 引言
活性粉末混凝土(RPC)是根据密实堆积原理配制出来的具有超高力学性能和高耐久性能的新型水泥基复合材料[1]。与普通混凝土相比,RPC混凝土改善了材料组分的颗粒级配,由级配连续、良好的活性组分组成[2],从而获得高强度、高韧性和高耐久性,其中掺加的钢纤维增加了RPC的强度和韧性,因而具有广阔的应用前景。文献[3-4]用不同掺合料取代RPC中的胶凝材料研究其力学性能,试验结果表明:高炉矿渣和粉煤灰部分替代胶凝材料,可降低RPC的收缩变形,提高混凝土的抗压强度和韧性。文献[5-6]通过试验与有限元模拟对比,分析钢纤维高强混凝土板的冲切性能,研究结果表明:混凝土强度随纤维掺量的增加而增加。文献[7]的研究表明:当硅微粉等量取代硅灰的质量比为40%时,28 d龄期抗压和抗折强度可以达到128.6 MPa和20.90 MPa。文献[8]基于试验基础,通过严格的数学推导,建立了RPC200单轴受压应力-应变的本构模型方程。文献[9]通过线性回归分析,得出了棱柱体与立方体抗压强度、弹性模量与棱柱体抗压强度关系的数学表达式。
但是RPC的工程应用还处于初级阶段,对其轴心抗压应力-应变的研究并不多,尚缺乏一套完整的规范和准则。本文通过RPC的轴心抗压试验,研究活性掺合量对立方体抗压强度、棱柱体抗压强度、弹性模量等力学性能的影响,建立RPC的单轴受压应力-应变曲线方程,为实际工程应用提供理论依据。
1 试验
1.1 材料配合比
本文采用单掺及混掺方式,研究不同掺合料对活性粉末混凝土的轴心抗压强度、弹性模量及受压应力-应变曲线的影响。鉴于在一定条件下,掺合料取代硅灰的质量分数超过50%条件下[3-4,10-11],其掺合量替代硅灰质量分数的增加对RPC强度、弹性模量等力学性能的提高有限,因此,在混凝土配合比设计中只讨论在标准养护28 d下不同掺合料等量(除硅微粉外)替代硅粉0%~60%活性粉末混凝土的力学性能、破坏形式以及应力-应变曲线。4批15组RPC配合比如表1所示。
1.2 试件制作及养护制度
分别进行了15组、每组3块、边长为100 mm的立方体试件抗压强度试验,以及15组、每组3块的100 mm×100 mm×300 mm棱柱体试件的轴心抗压试验,制作过程如下:

表1 不同掺合料替代不同比例硅粉RPC配合比
(Ⅰ)按配比确定各材料用量,为防止纤维结团,先将水泥、矿粉、石英砂倒入搅拌桶内,干搅1~2 min,然后再将钢纤维分批倒入搅拌桶内。
(Ⅱ)量取相应质量的水、减水剂,将高效减水剂和50%的水均匀混合,慢速搅拌2~3 m in。
(Ⅲ)加入剩余的水,快速搅拌2~3 min后将拌合物装入钢模中,装料的同时手工压实,尽量使试块密实,最后放在振动台上振捣2 min,试件自然养护24 h后拆模,并在标准养护条件下养护28 d(见图1)。
试验按照国家标准《普通混凝土力学性能试验方法标准》(GB/T50081—2002)进行,加载设备采用桂林理工大学结构实验室YAW-2000B型电液式压力试验机,数据采集仪采用DH3816静态应变测试系统。

图1 养护中的一组试块
2 结果分析
将试验记录的数据整理,得到15组试件立方体抗压强度fcu、棱柱体抗压强度fc、峰值应变ε0和弹性模量Ec的平均值,详见表2。
2.1 RPC变形与破坏特征
RPC轴心受压试件的破坏过程与普通混凝土试件一样,经历了弹性阶段、弹塑性阶段、裂缝扩展和试件压碎等过程,不同的是由于掺加了钢纤维,RPC试件破坏时并没有被压酥散落,而是仍然保持整体(见图2)。试件达到最大荷载前,试件表面很少出现裂缝,达到最大值后,立方体试块表面出现明显裂缝,特别是棱角处裂缝最大,试件中部外鼓开裂;而棱柱体试件应力到达峰值后,很快出现斜裂缝并迅速发展成主斜裂缝。无论是立方体试块还是棱柱体试块,由于掺加了钢纤维,在破坏过程中,伴随清晰的“嘣嘣”声,裂缝面的钢纤维逐渐被拔出。
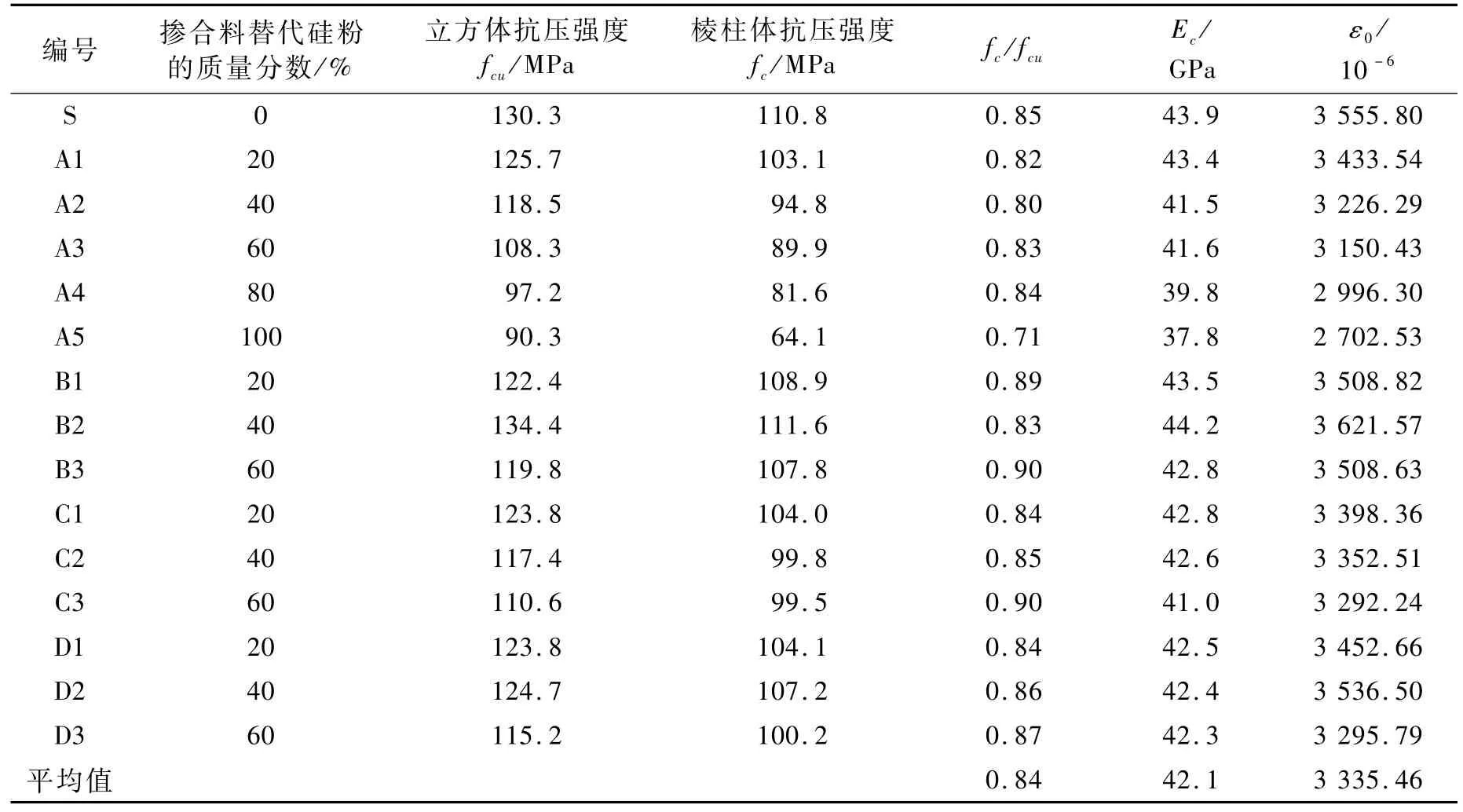
表2 力学性能试验结果
2.2 掺合料掺量对RPC力学性能的影响
由表2可知:当掺合料掺量为0%~20%时,RPC抗压强度随掺合料掺量的增加而降低,掺硅微粉的RPC强度降低幅度最小,降低4.6 MPa,掺粉煤灰的RPC强度降低幅度最大,强度降低7.9 MPa;掺合料掺量为20%~40%时,掺硅微粉和掺石英粉的RPC抗压强度随掺量的增加而降低,而掺粉煤灰RPC和双掺粉煤灰石英粉的RPC抗压强度却随掺量的增加而提高;当掺合料掺量达到40%时,所有试块的RPC抗压强度都在120 MPa以上,特别是掺粉煤灰RPC试件,抗压强度达到最高值134.4 MPa,比单掺硅粉的抗压强度提高了3%左右;掺合料掺量为40%~60%时,RPC抗压强度随掺合料掺量的增加而降低,掺硅微粉试件强度降低22 MPa,掺石英粉的试件强度降低19.7 MPa,双掺粉煤灰石英砂试件强度降低15.1 MPa,掺粉煤灰试件强度降低10.5 MPa。

图2 RPC抗压试件破坏形态
图3为掺合料掺量对RPC抗压强度的影响,从图3可以直观地看出4种不同掺合料对抗压强度影响作用由大到小为:粉煤灰>单掺硅粉>双掺粉煤灰、石英粉>硅微粉>石英粉。从市场调查材料成本来看,成本由高到低顺序为:硅粉>硅微粉>石英粉>粉煤灰。因此,掺入40%以下的粉煤灰替代价格昂贵的硅粉不仅能提高RPC的强度,还将产生很好的经济效益。粉煤灰的增强机理主要有以下两方面的内容:(Ⅰ)形态效应和微集料效应:粉煤灰的颗粒粒径非常小,远小于水泥颗粒,颗粒呈球形,表面光滑。在配制低水胶比RPC混凝土时,随着搅拌的进行,粉煤灰产生“滚珠”效应,从而提高RPC浆体的流动性。同时粉煤灰还起到填充颗粒间隙的作用,改善浆料粒径级配,提高浆体密实度。(Ⅱ)火山灰效应:在水化初期,粉煤灰的火山灰反应很慢,主要产生物理填充作用,改善掺合料的微观结构以推进复合胶凝材料抗压强度的提高。水化后期粉煤灰的火山灰效应充分发挥出来,粉煤灰中的SiO2在常温下与水泥水化产物氢氧化钙(Ca(OH)2)发生二次水化反应,生成大量凝胶,填充在骨料间,进一步改善微观结构,提高浆体密实度,从而提高混凝土强度。同样的活性作用,用硅微粉和石英粉代替40%以下的硅粉,也能产生较好的经济效益。
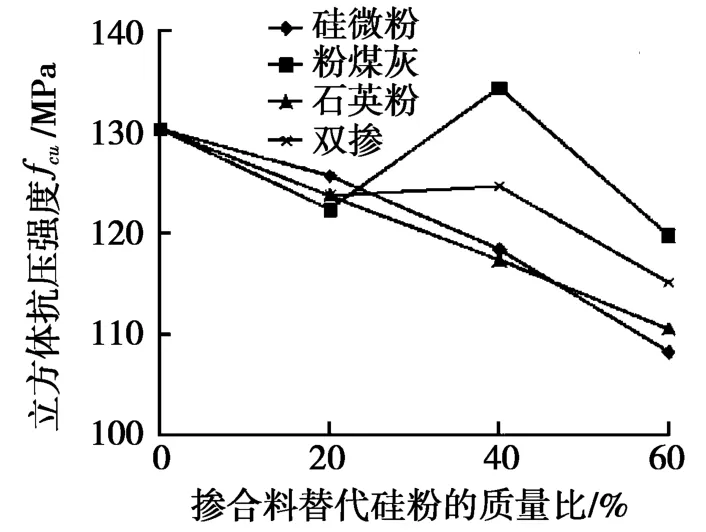
图3 掺合料掺量对RPC抗压强度的影响
2.3 RPC棱柱体抗压强度与立方体抗压强度的关系
表2给出了RPC棱柱体与立方体强度的关系,由表2可看出:RPC材料的轴心抗压强度随立方体抗压强度的增加而增加,棱柱体强度与立方体强度存在着fc/fcu∈(0.8~0.9)的换算关系,平均值为0.84,比文献[13]给出C50及以下混凝土的比值(0.76)高;与C80的比值(0.82)接近[14]。本文通过15组试验数据,拟合出RPC材料的轴心抗压强度与立方体抗压强度计算公式(见图4):fc=0.84 fcu+1.35 MPa,其中fc、fcu分别为混凝土的轴心抗压强度与立方体抗压强度,单位为MPa。
2.4 RPC弹性模量与立方体抗压强度的关系
弹性模量是混凝土重要的性能指标,它反映了混凝土应力与应变之间的关系。由表2可知:混凝土的弹性模量随强度单调增长,但两者之间并不呈线性关系。本文通过15组弹性模量的数据,拟合出公式适应于RPC的弹性模量与立方体抗压强度的计算公式如图5所示。
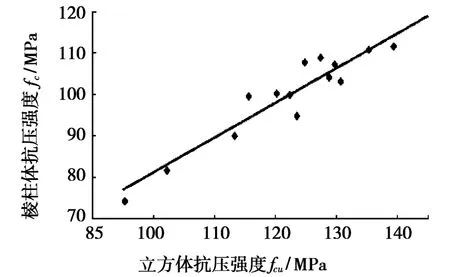
图4 RPC棱柱体抗压强度与立方体抗压强度的关系

图5 RPC弹性模量与立方体抗压强度关系
2.5 RPC峰值应变与RPC棱柱体抗压强度的关系
试验试件实测的峰值应变ε0见表2。RPC峰值应变与棱柱体抗压强度关系见图6。由表2和图6可看出:RPC峰值应变随棱柱体抗压强度的增大而单调增大,比普通混凝土和一般高强混凝土峰值应力都大[15];同时掺合料掺量对峰值应变的影响不明显。本文通过对试验数据进行回归分析和数据拟合,得到RPC峰值应变与棱柱体抗压强度的关系式ε0=(23.10 MPa-1fc+1 030)×10-6。在相同配比和养护制度条件下,与文献[16]给出的掺钢纤维RPC峰值应变与棱柱体抗压强度关系式类似。
3 RPC应力-应变曲线方程
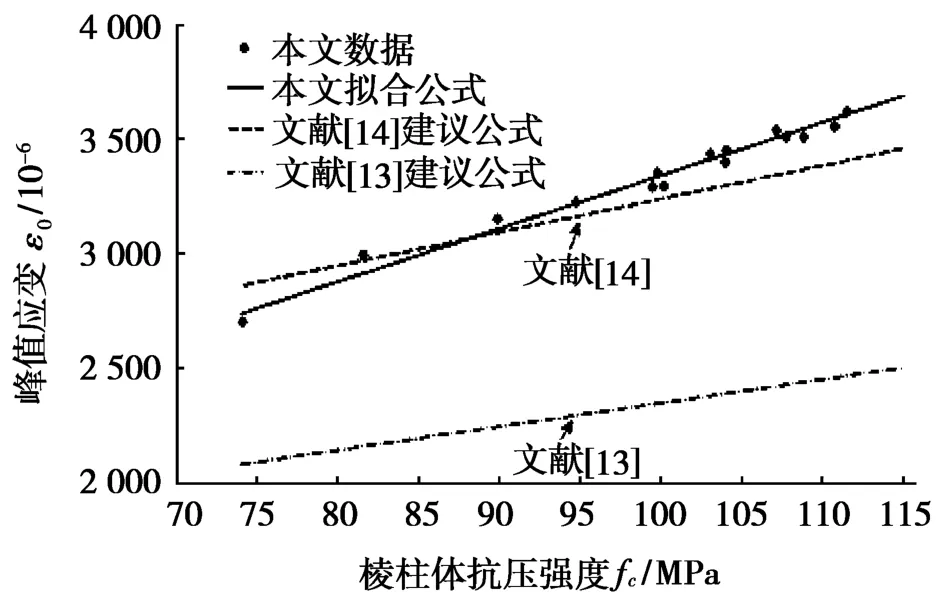
图6 RPC峰值应变与棱柱体抗压强度关系
混凝土应力-应变曲线是混凝土力学性能的一个重要指标,是构件应力分析、建立强度和变形计算理论必不可少的依据。与普通混凝土破坏变形一样,经历了骨料与水泥晶体的弹性变形、弹塑性变形、裂缝快速发展不稳定和压酥脆性破坏等阶段。混凝土的破坏机理和裂缝的发展变化过程都可用应力-应变曲线来解释,主要是由于混凝土内微裂缝的扩展所致。目前,国内外针对混凝土单轴受压应力-应变全曲线已有大量研究,尽管各学者提出的数学函数类型和表达式各不相同,但全曲线具有的形状及特征均得到研究人员的一致公认。
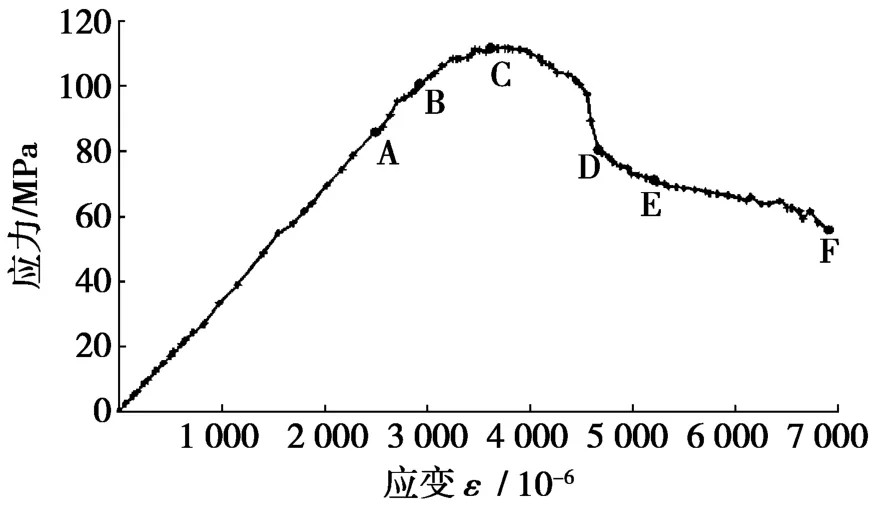
图7 RPC实测应力-应变全曲线
3.1 RPC破坏特征与应力-应变曲线特征
RPC棱柱体受压的应力-应变全曲线见图7,以B2组配比试验值说明应力-应变全曲线特征。由图7可看出:RPC棱柱体受压的应力-应变全曲线与普通混凝土典型应力-应变全曲线基本一致,曲线上有6个特征点:A、B、C、D、E、F表示混凝土在受压状态下的不同阶段。
(Ⅰ)从开始加载至比例极限A点(σ=0.6 fc~0.8 fc),应力-应变关系接近直线,混凝土的变形主要是骨料与水泥颗粒的弹性变形,裂缝主要表现为混凝土内的黏结裂缝,但裂缝处于稳定状态,这个阶段的应力比普通混凝土增大了近1倍,说明RPC的开裂荷载提高了1倍,具有非常优异的抗裂性能。
(Ⅱ)A-B(σ=0.8 fc~0.9 fc)为弹塑性阶段,B点称为临界点。随着荷载的增大,裂缝的数量和宽度急剧增加,裂缝演变为通缝,但裂缝仍处于稳定扩展阶段。
(Ⅲ)超过B点,混凝土进入裂缝快速发展的不稳定状态直至峰值点C,混凝土内裂缝形成与水平方向45°的破坏面,荷载将由混凝土分割的小柱体承担。
(Ⅳ)超过峰值点C后,可见裂缝迅速发展,多条裂缝沿着试件成型面对角线贯通,混凝土损伤严重,应力急剧下降,而应变变化无几,曲线到达拐点D。
(Ⅴ)曲线下降到D点以后,应力-应变曲线凸向x轴发展,在此阶段出现曲率最大点E称为收敛点。裂缝宽度进一步扩大,钢纤维随着应变的增加沿裂缝面逐渐脱黏拔出,试件发出急促的钢纤维被拔出的声音,伴有爆裂声,同时碎块向四周飞溅。
(Ⅵ)应力超过曲线E点后,试件进入残余强度阶段。在该阶段,残余强度主要由开裂后的试件残体承担。此时,有大量被剪碎的RPC碎屑从裂缝中掉落,曲线到达F点,试件加载结束。
3.2 RPC应力-应变曲线方程
针对普通混凝土受压应力-应变曲线方程,大量专家学者提出了多种函数类型和数学表达式,如Hognestad的多项式[17]、Young的指数式、Desayi-Krishman的有理式[18]和Umemura的指数式[19]等。由于活性粉末混凝土应力-应变曲线形式与普通混凝土类似,其本构模型可基于现有的本构模型形式[20-23]进行研究。
3.2.1 上升段曲线
对于上升段曲线(0≤x≤1),采用多项式进行拟合。考虑到钢纤维活性粉末混凝土的强度较高,弹性部分较长,故选择次数较高的多项式,本文选择过原点的6次多项式进行推导拟合。

(Ⅰ)当x=0时,y=0,满足式(1)的要求;当x=1时,y=1,则有:


将曲线方程简化为:
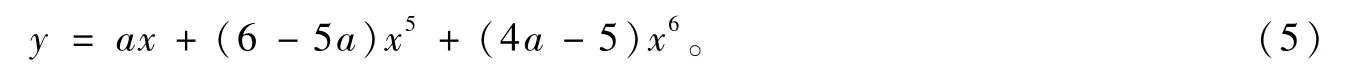
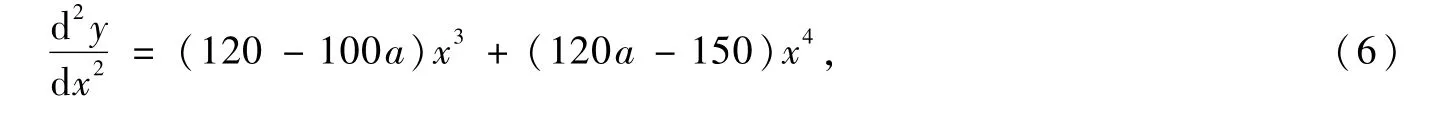
3.2.2 下降段曲线
试验设备和试验方法对应力-应变曲线下降段有很大的影响,因而离散性较大。文献[22]针对各研究学者的本构模型,提出了更适合拟合曲线下降段的有理式方程。本文采用既满足要求且较为简单的有理式方程:

3.3 RPC单轴受压应力-应变全曲线参数值的确定
据上所述,对12组不同掺合料掺量不超过60%的RPC无量纲坐标应力-应变试验曲线进行数据拟合,图8为拟合得到的理论曲线与试验曲线的比较。图8中,字母A、B、C、D分别表示4种不同活性掺合料,数字1、2、3分别代表试件在该组的编号。由图8可看出:上升段曲线吻合良好,下降段曲线离散性较大,但在理论曲线范围内,拟合方程有效。基于本文试验结果,各种掺合料替代硅粉百分量的RPC受压应力-应变曲线方程为:

4 结论
(1)与普通混凝土一样,RPC同样经历弹性变形、裂缝发展的稳定阶段、裂缝迅速发展不稳定和试件破坏等4个阶段。但由于RPC集料颗粒级配连续良好,提高了浆体的密实度,弹性变形阶段比普通混凝土长很多;再者由于掺加了钢纤维,延迟了RPC混凝土裂缝的开展,试件破坏时,RPC试块仍能保持呈整体,而不是像普通混凝土那样被压酥散架。
(2)掺合料对RPC抗压强度的影响由大到小排列顺序为:粉煤灰>硅粉>双掺粉煤灰、石英粉>硅微粉>石英粉。当掺入40%粉煤灰替代部分价格昂贵的硅粉时,试件的抗压强度提高幅度最大,因此,在RPC配比中加入适量的粉煤灰将产生很好的经济效应。
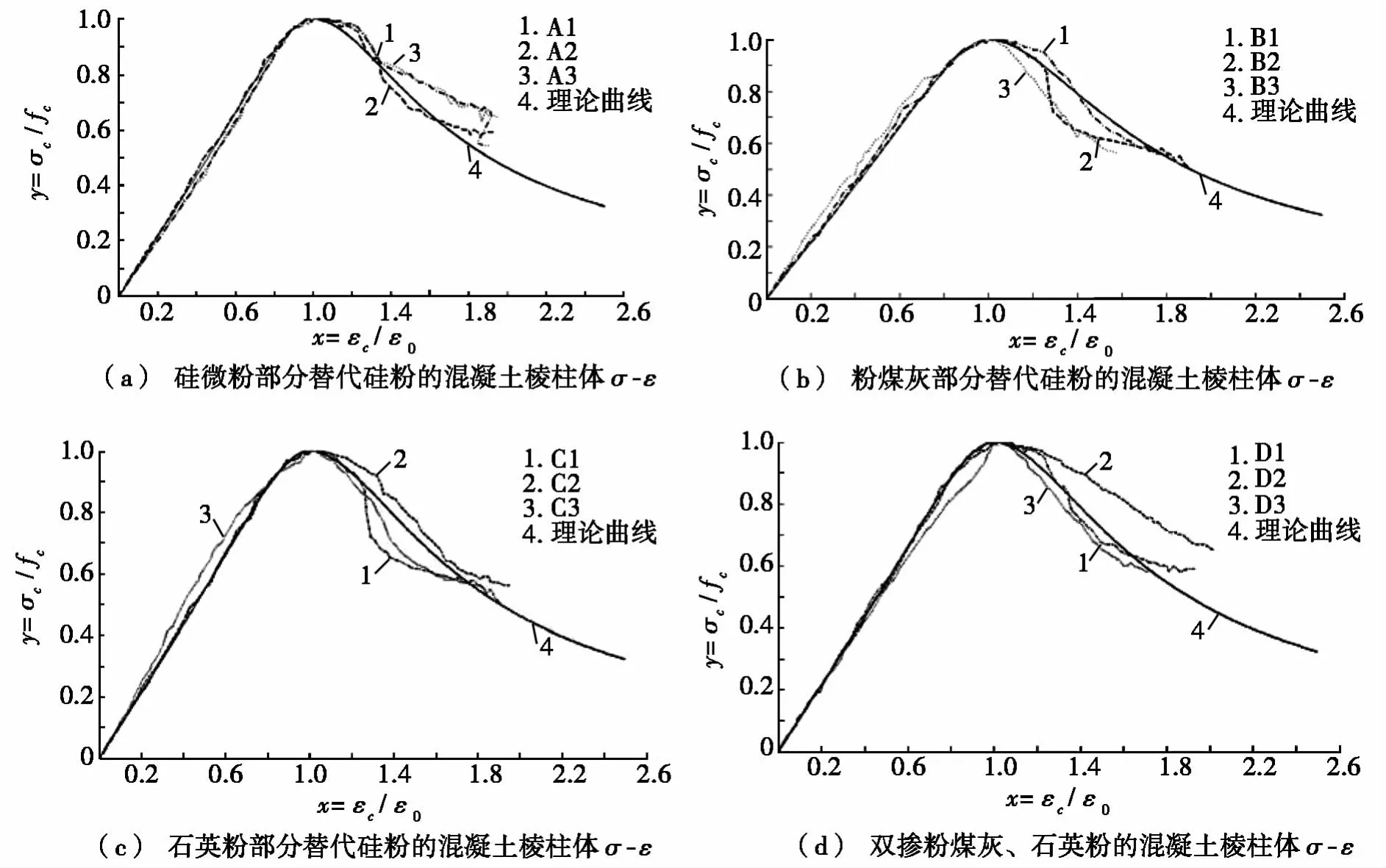
图8 理论曲线与试验曲线对比图
(3)在标准养护28 d条件下,棱柱体抗压强度随立方体抗压强度单调增加,强度比值fc/fcu为0.8~0.9,两者的换算关系为fc=0.84 fcu+1.35 MPa;将试验数据进行拟合,得到RPC弹性模量与棱柱体立方强度的拟合方程式RPC的峰值应变明显高于普通混凝土,将试验数据进行拟合,得到RPC受压峰值应变与棱柱体抗压强度的关系曲线方程:ε0=(23.10 MPa-1fc+1 030)×10-6。
(4)由于钢纤维活性粉末混凝土RPC强度较高,弹性部分较长,试件破坏后的应力-应变离散性较大。对于RPC的轴心受压应力-应变全曲线方程式,上升段选择通过原点的6次多项式进行推导拟合,下降段曲线方程采用文献[24]提出的有理式方程:
[1] Dugat J,Roux N,Bernier G.Mechanical Properties of Reactive Powder Concretes[J].Materials and Structures,1996,29(4):233-240.
[2] Yang S L,M illard S G,Soutsos M N,et al.Influence of Aggregate and Curing Regime on the Mechanical Properties of Ultra-high Performance Fibre Reinforced Concrete(UHPFRC)[J].Construction and Building Materials,2009,23(6):2291-2298.
[3] Yazlcl H,Yardlmcl M Y,Aydin S,et al.Mechanical Properties of Reactive Powder Concrete Containing M ineral Admixtures Under Different Curing Regimes[J].Construction and Building Materials,2009,23(3):1223-1231.
[4] Yazlcl H,Yard lmcl M Y,Yigiter H,et al.Mechanical Properties of Reactive Powder Concrete Containing High Volumes of Ground Granulated Blast Furnace Slag[J].Cement and Concrete Composites,2010,32(8):639-648.
[5] 谢晓鹏,黄功学,高丹盈.钢纤维钢筋混凝土板冲切性能ANSYS分析[J].河南科技大学学报:自然科学版,2012,33(1):54-58.
[6] 张伟,张晓庆,杨大峰.钢纤维混凝土腐蚀试验研究[J].河南科技大学学报:自然科学版,2013,34(4):65-69.
[7] 宋正林.天然硅质掺合料活性粉末混凝土研究[D].武汉:武汉理工大学,2011.
[8] 马亚峰.活性粉末混凝土RPC200单轴受压本构关系研究[D].北京:北京交通大学,2006.
[9] 郝文秀,徐晓.钢纤维活性粉末混凝土力学性能试验研究[J].建筑技术,2012,43(1):35-37.
[10] 陈友治,宋正林,许闽,等.天然硅质掺合料活性粉末混凝土(RPC)研究[J].武汉理工大学学报,2011,33(6):26-30.
[11] 赵庆新,孙伟,缪昌文.粉煤灰掺量和水胶比对高性能混凝土徐变性能的影响及其机理[J].土木工程学报,2009,42(12):76-82.
[12] 金凌志,祁凯能,曹霞.高强钢筋活性粉末混凝土简支梁受剪性能试验研究[J].武汉理工大学学报,2013,35(8):108-113.
[13] 中华人民共和国住房和城乡建设部.混凝土结构设计规范GB50010—2010[M].北京:中国建筑工业出版社,2010.
[14] 王志军,蒲心诚.超高强混凝土单轴受压性能及应力应变曲线的试验研究[J].重庆建筑大学学报,2000,22(增刊):27-33.
[15] 吴炎海,何雁斌,杨幼华.活性粉末混凝土(RPC200)的力学性能[J].福州大学学报:自然科学版,2003,31(5):598-602.
[16] 曾建仙,吴炎海,林清.掺钢纤维活性粉末混凝土的受压力学性能研究[J].福州大学学报:自然科学版,2005,33(增刊):132-137.
[17] Hognestad E,Hanson N W,McHenry D.Concrete Stress Distribution in Ultimate Strength Design[J].ACI,1955,52(12):455-480.
[18] Desayi P.Determination of the Maximum Crack Width in Reinforced Concrete Members[J].ACI,1976,73(8):473-477.
[19] Watstein D.Effect of Straining Rate on the Compressive Strength and Elastic Proterties of Concrete[J].ACI,1953,49(4):729-744.
[20] 过镇海.混凝土的强度和变形—实验基础和本构关系[M].北京:清华大学出版社,1977.
[21] 谭彬.活性粉末混凝土受压应力应变全曲线的研究[D].长沙:湖南大学,2007.
[22] 王志建.活性粉末混凝土(RPC)二轴受压本构关系和破坏准则研究[D].北京:北京交通大学,2008.
[23] 陈爽,陈宜虎,梁进修.碳纤维加固锈蚀钢筋混凝土梁的疲劳抗弯性能[J].河南科技大学学报:自然科学版,2014,35(1):58-62.
[24]Sargin M.Stress-Strain Relationships for Conerete and the Analysis of Struetural Conerete Seetions[R].Canada:University of Waterloo,1971.
TU312.1;TU317.1
A
1672-6871(2014)05-0055-08
国家自然科学基金项目(51368013);广西科技攻关基金项目(桂科攻0995004);广西重点实验基金项目(11-cx-04)
金凌志(1959-),女,广西桂林人,教授,硕士生导师,研究方向为结构工程.
2014-02-22
