Sound Radiation Characteristics of A Submerged Stiffened Cylindrical Shell Subjected to Internal Acoustic Excitations

GUAN Shan-shan,DENG Hai-hua,CHEN Ming

(Wuhan Secondly Research Institute of Ship-designing,Wuhan 430064,China)

Sound Radiation Characteristics of A Submerged Stiffened Cylindrical Shell Subjected to Internal Acoustic Excitations

GUAN Shan-shan,DENG Hai-hua,CHEN Ming

(Wuhan Secondly Research Institute of Ship-designing,Wuhan 430064,China)

A method for calculating the outside sound radiation of an enclosure cylindrical cabin housing machines which produce both internal noise and mechanical forces is proposed.According to Flügge theory and the Helmholtz equation,a‘stiffened cylindrical shell-cavity-outside radiated sound field’coupling equation is presented.To solve this coupling equation,the displacements of the cylinder are expanded in a series of its eigenmodes.The displacements of the cavity are expressed by acoustic modes.And the inside and outside sound pressures are treated as reaction forces on the shell. Then according to the orthonormal relations of modes of the shell,the solution method of the coupling vibration equations expressed by shell’s displacements is given.The sound radiation characteristics of a submerged stiffened cylindrical shell inspirited by harmonious exciting forces are reappeared. The results agree well with the relative reference papers,thus demonstrating the rationality of the theoretical method.Then the effects of the cut-off mode order numbers of the cavity on the calculation accuracy are described.Finally,the influences of different positions of an interior source on acoustic of the shell are obtained,and the comparisons of sound radiation properties of interior sources which have the same phases and different phases are carried out.The theoretical solution and the discussion are favorable for noise reduction of submerged stiffened cylindrical shells.

finite stiffened cylindrical shell;internal acoustic excitations; sound radiation characteristics;cut-off mode

1 Introduction

The sound radiation of a submarine housing machines that produce both noise and vibration is composed by two parts,as shown in Fig.1:the first part is the acoustic by the machine noise itself exciting the structures called‘Airborn Sound’;the second part is the vibro-acoustic of submarine excited by the vibratory force of machines,called‘Structureborn Sound’.The sound radiation of submarine induced by mechanical forces has been decreased in effect with the development and management of silent equipments and isolation technique.So the sound radiation of submerged shells excited by interior air source has received a great deal of attention recently.

Stiffened cylindrical shells are widely used in many structural applications,such as submarine hulls,torpedoes,and waterborne missiles.The sound radiation of a submerged stiffened cylinder and the characteristics of a three-dimensional acoustical enclosure have been respectively investigated in more detail by many researchers.And the acoustic radiation of shells excited by driving forces in infinity acoustic medium[1-2]and the characteristics and active noise control of the internal sound pressure field surrounded by flexible structures[3-5]have been discussed by a majority of investigation.Yet very little work can be found on the external sound radiation of submerged closed stiffened cylindrical shells excited by acoustic excitations.

This paper proposes a method to calculate the outside sound radiation of machines in an enclosure submerged cylindrical cabin which produces both internal noise and mechanical forces.According to Flügge theory,the Helmholtz equation and the previous researches[6-7],a‘stiffened cylindrical shell-cavity-outside radiated sound field’coupling equation is described and solved by using the modal superposition principle.The sound radiation characteristics of a submerged stiffened cylindrical shell excited by interior sources are obtained.And the influences of different positions of the interior sources and different phases of sources on the sound radiation of the shell are also analyzed.This discussion is favorable for noise reduction of a hull.

2 Physics model and theoretical development

Fig.1 Theoretical model of an engine cabin and the coordinate system

The physics model is a submerged stiffened cylinder,as shown in Fig.1.It is assumed that the shell is simply supported on two semi-infinite rigid baffles.Junger and Feit[8]showed that mutual reactances were generally negligible.The structure response ranges in linear elastic scopeand the inside and outside fluid are satisfied with linear acoustic conditions.R,h and L denote the radius,the thickness,and the total length of the shell,respectively.l is the spacing of rings.F denotes vibratory forces.Q denotes point sound sources.ρ1and c1are the density and acoustic velocity of the external sound field respectively.ρ2and c2are the density and acoustic velocity of the internal sound field respectively.

Using a cylindrical coordinate systemz,（）θ,u,v and w are the orthogonal components of the shell displacement in the axial,circumferential and radial directions respectively,as shown in Fig.1.

2.1 Equations of motion for a submerged stiffened cylindrical shell

The Flügge equation of thin shell is applied to describe the motion of the submerged cylinder.Using deformation harmonious conditions of the interface,the effects of stiffeners are treated as counter forces and counter moments acting on the cylindrical shell.So the solution of acoustic pressure is changed to the solution of coupling vibration equation.The coupling vibration equations of the acoustic-fluid-structure are obtained:

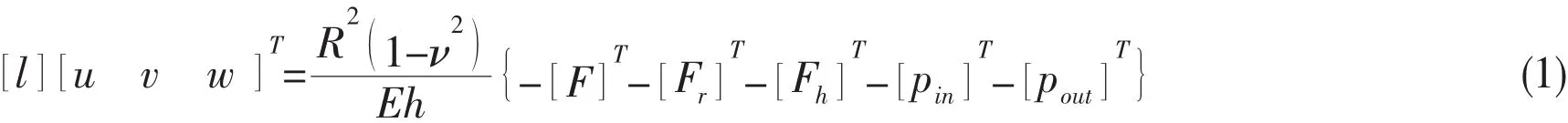
where［l］is Flügge’s operators(see Ref.[9]).［F］is the generalized force matrix for point excitations applied to the shell.Fr［］is the generalized counter forces martix of rings.Fh［］is the generalized counter forces matrix of longitudinal girders.pin［］andpout［］are the interior and exterior acoustic pressure vector loading on the shell surface respectively.As part of this equation,］and［pout］are already studied by Refs.[6]and[7].Main attention is paid to the acoustic pressure of the cavitypin［］in this paper.

2.2 Equations of motion for a cylindrical-shaped cavity

The cylindrical-shaped cavity contains some harmonic point sound sources.is the number of the sources.The acoustic pressure inside the cavity satisfies the non-homogeneous wave equation.According to the continuity of velocities on the different parts of the cavity walls,the equation of pincan be expressed as follows[3]:

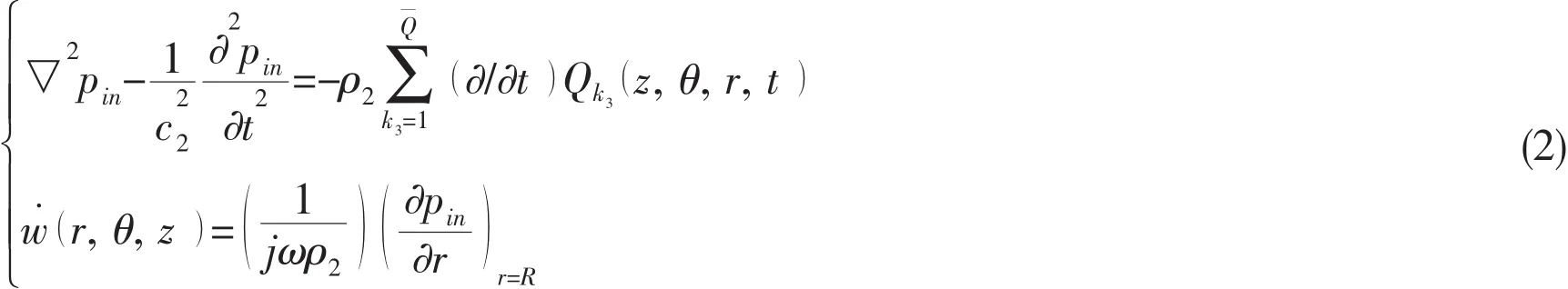
where Qk（z,θ,r,t）is the volume velocity distributed function of the k3th point sound source.

3k3values from 1 tois the serial number of the harmonic sources.And pincan be given by pin（z,θ,r,t）=pin（z,θ,r） e-jωt.ω is the angular frequency.

According to the Green function and Gauss integral theory,pincan be expressed as a Kirchholff-Helmholtz integral expression based on Eq.(2)[10]:

where →r=（z,θ,r）is the coordinate vector of an arbitrary point in the cavity.）and →rsare the sound pressure and the coordinate vector of an arbitrary point on the walls of the cavity, respectively.r→k3is the position coordinate vector of the k3th sound source,and r→k3=zk3,θk3,rk3

（）. S is the surface of the walls. Gcr→,r→κ,（）ωwhich is the Green’s function of the cavity satisfies the Neumann boundary condition.It can be expressed as follows:

where φn~r→（）and ωn~are the mode shape and the angular frequency of the n~th order mode of the cavity,respectively.is the volume of the closed cylindrical-shaped cavity.

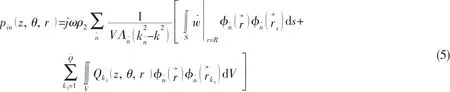
2.3 Solution to the coupling equation

This finite-shell satisfies the simply-supported boundary condition.General solutions to the equations of motion for the cylindrical shell can be assumed as:

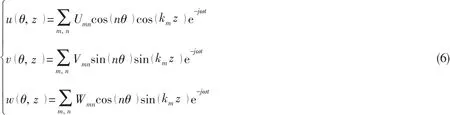
where 0≤z≤L,0≤θ≤2π,m=1:∞,n=0:∞.m is the longitudinal half-mode number.n is thecircumferential mode number.kmis the axial wavenumber,km=mπ/L,contains the unknown wave amplitudes of the（m,n） th order mode of the shell.

23

The interior pressure is the sum of two componentsSubstituting Eqs.(6)and(7)into Eq.(5)yields:

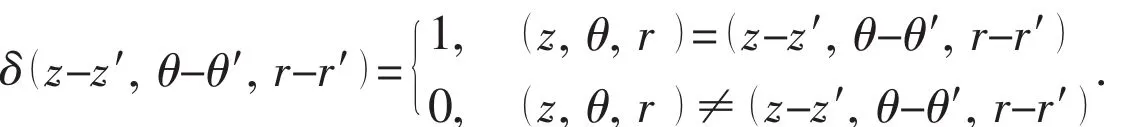
couplemnn~are the coupling coefficients which express the relationship of them,（）nth order mode of the shell and the）th order mode of the cavity.

According to the orthonormal relations of modes of the shell,Eq.(1)is multiplied by a orthogonal transform matrixsulting in:

where,D=R2（1-ν2）/（Eh）,p=1:∞,q=0:∞,are the decoupling expressions of Pin1and Pin2after orthogonal transforming,respectively.

The structure-cavity coupling analysis can be achieved by solving Eq.(11)composed by max（m）×max（n）×3 equations.Thereforecan be obtained and three main characteristic parameters of acoustic radiation will be used in the next analysis,which are defined as follows:

The outside acoustic power:

The mean square radial velocity of the shell:

The radiant efficiency of the shell:

where Vr（z,θ,R）is the radial velocity of the shell surface.Vr*（z,θ,R）is the conjugate complex quantity of Vrz,θ,（）R.

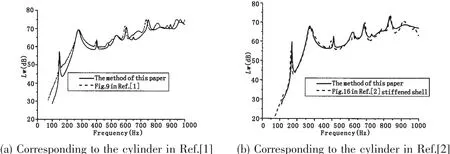
Fig.2 Acoustic radiated power level

2.4 Validation of the analytical method for a force driving

A submerged cylinder excited by a unit force is examined.To confirm the validity of the analytical method presented in this work,results in Refs.[1-2]are represented here.The acoustic power levels of the shell are shown in Fig.(2).A small difference is observed,thus the rationality of the theoretical solution method is demonstrated.

3 Numerical results

The stiffened cylinder in water used in the numerical study is L/R=3.0,R/h=115.38,L/l= 15.The ring-stiffeners’type is Γ22a.The shell and the stiffening beams are of the same material with Young’s modulus E=2.1×1011N·m-2,Poisson’s ratio ν=0.3 and density ρs=7 800 kg·m-3.

The material property of exterior sound field:ρ1=1.0×103kg/m3,c1=1 500 m/s.

The material property of interior sound field:ρ2=1.29 kg/m3,c2=340 m/s.

The driving unit internal source is applied at（L/2,0°,R/2）.

3.1 The coupling relationship between the interior sound field and the shell

The structure-cavity coupled coefficients couplemnn~are given in Tab.1.Clustered coupling characteristics of the coupled structure-cavity can be seen obviously,that is,the values of couplemnn~depend on the even or odd quality of m,n,n¯1and n¯2.

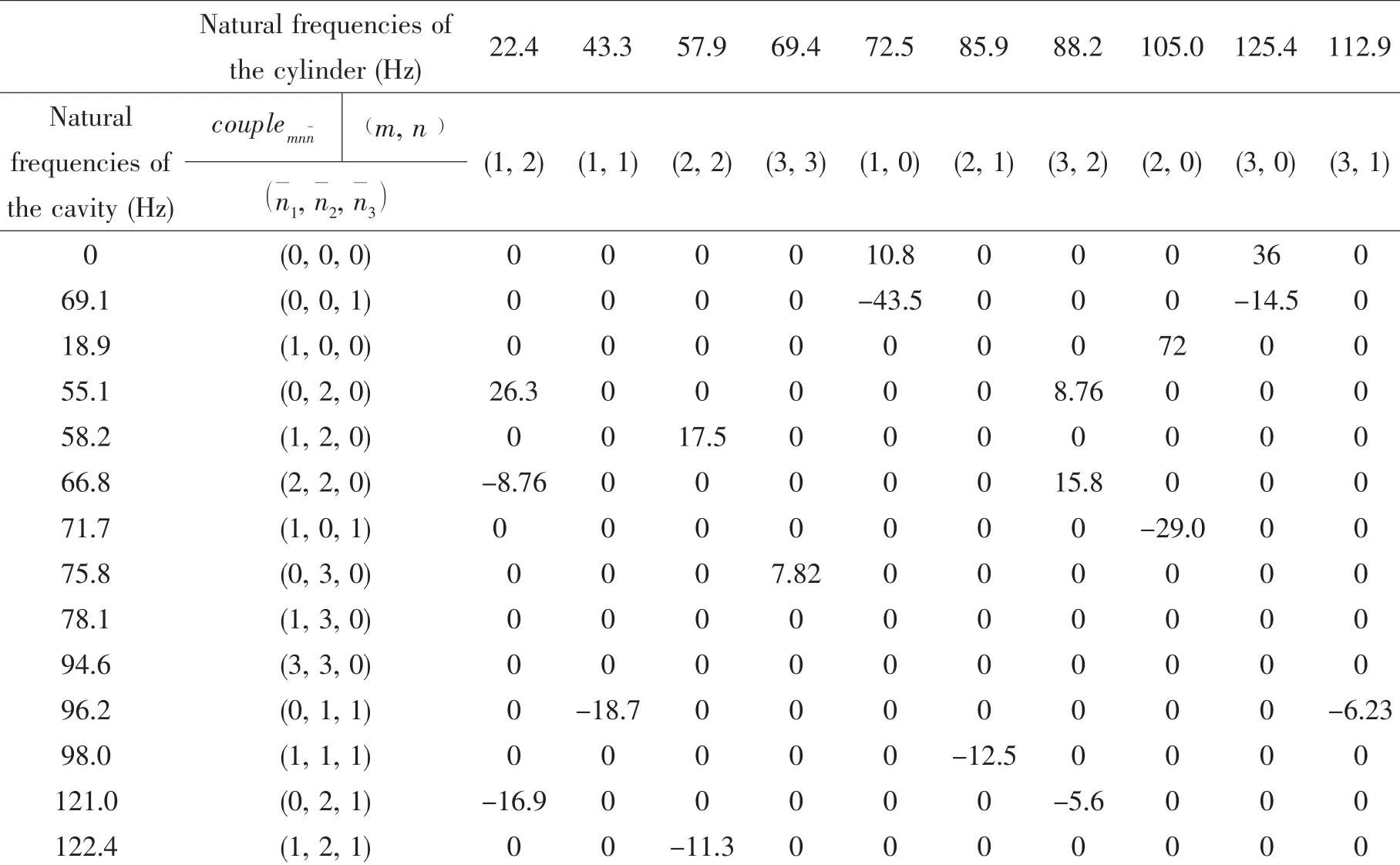
Tab.1 Coupled coefficients couplemnn~of the structure-cavity

continue Tab.1

3.2 The radiation impedance of the shell to the internal sound field About the interior sound field,we have:

Figs.3(a)and 3(b)present the values of the R）andof the shell corresponding to m=p=1,n=q=2,¯n=1:7.And Figs.2(c)and 2(d)present the values of the R3and Iof the shell corresponding to m=p=2,n=q=2,¯n=1:7.These results show that1the values of the Rand Irapidly decrease with the increase of the frequency. For high frequenciestends to 0,that is the effect of high rank modes of the cavity on the acoustic characteristics of the shell can be ignored.

3.3 The influence of the cut-off mode order of the cavity on the calculation accuracy

A majority of investigation have discussed the effect of the cut-off mode orders of the shell on the calculation accuracy of‘Structureborn Sound’.From Fig.4(a)and(b),when theshell of this paper is excited by a force,max（ m,n）=（25,25）is enough for calculation accuracy of‘Structureborn Sound’as the frequency range from 5 Hz to 300 Hz.So this chapter primarily discusses the effect of the cut-off mode orders of the cavity on the calculation accuracy of the‘Airborn Sound’.

Fig.4 The effect of the cut-off mode orders of the shell on the calculation accuracy of‘Structureborn Sound’

Fig.5(a)shows the acoustic radiated power levels and mean square radial velocities of the shell as max（¯n1,¯n2,¯n3）are（4,4,4）,（8,8,8）,（15,15,15）and（25,25,25）.It can be seen that the levels as（15,15,15）and（25,25,25）have small difference.Then Fig.5(b) gives the levels as max（¯n1,¯n2,¯n3）are（15,15,15）,（15,4,4）and（4,4,4）,respectively.Through analysis and comparing the performance,it can be seen that the effect of the maximal value of longitudinal mode of the cavity ¯n1is bigger than maximal values of ¯n2and ¯n3on the calculation accuracy.And for this cylinder,max（15,4,4）can satisfy the calculation accuracy of the‘Airborn Sound’as the frequency range from 5 Hz to 300 Hz.

Deservedly with the frequency increases,the maximal values ofm,（）nof the shell and maximal values ofof the cavity must increase jointly to satisfy the calculation accuracy.

Fig.5 The effect of the cut-off mode orders）of the cavity on the calculation accuracy of the‘Airborn Sound’

4 The influence of the internal sound sources on vibro-acoustic characteristics of the submerged cylinder

4.1 The influence of the position of an internal point sound source on vibro-acoustic characteristics of the submerged cylinder

(1)The influence of the radial position of an internal point sound source

Figs.6(a),(b)and(c)present the mean square radial velocity,the radiant efficiency and the acoustic power level of the cylinder excited by a unit internal source whose positions are（L/2,0,0）,（L/2,0,R/4）,（L/2,0,R/2）and（L/2,0,R-）,respectively at the frequency range from 10～300 Hz.R-denotes the source very close to the inner surface of the shell.The influ-ence of the radial position of the internal source on the mean square radial velocity is greater than that on the acoustic power level.And as the frequency increases,the influence on the mean square radial velocity gradually decreases.Figs.6(a)and(b)present the external sound pressure of the outside surface of the shell at x=L/2.

Due to the locationL/2,0,（）0 is the modal node of the radial mode and the axial mode, when the source is located at this place,the number of peaks of the curves is less than that at other places,and except few frequencies the radiant efficiencies are higher and the mean square radial velocities are smaller.When the source is located atL/2,0,（）0,the external sound pressure are well-proportioned both at the frequency of 30 Hz and 100 Hz.And when the source is located atL/2,0,R-（）which is close to the inner surface of the shell,the mean square radial velocities are bigger than those at other places.Figs.7(a)shows that for the same angles when the source is located atL/2,0,R-（）the external sound pressures mostly take bigger values than those at other positions,and when it is located atL/2,0,（）0the external sound pressures mostly take smaller values.

Fig.6 The shell excited by an internal point sound source at different radial positions

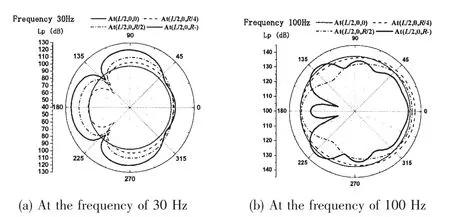
Fig.7 Directivity patterns of the outside surface of the shell at x=L/2

(2)The influence of the axial position of an internal point sound source

Figs.8(a),(b)and(c)present the mean square radial velocity,the acoustic power level and the radiant efficiency of the cylinder excited by a unit internal point sound source whose coordinates（z,θ,r）are（L/2,0,R/2）and（L/4,0,R/2）,respectively at the frequency range from10～300 Hz.The influence of the axial position of the internal source on the mean square radial velocity and the acoustic power level is small,and the influence gradually decreases with the frequency increases.From Fig.8(c),the effect of the axial position on the radiant efficiency is notable as f＜100 Hz.

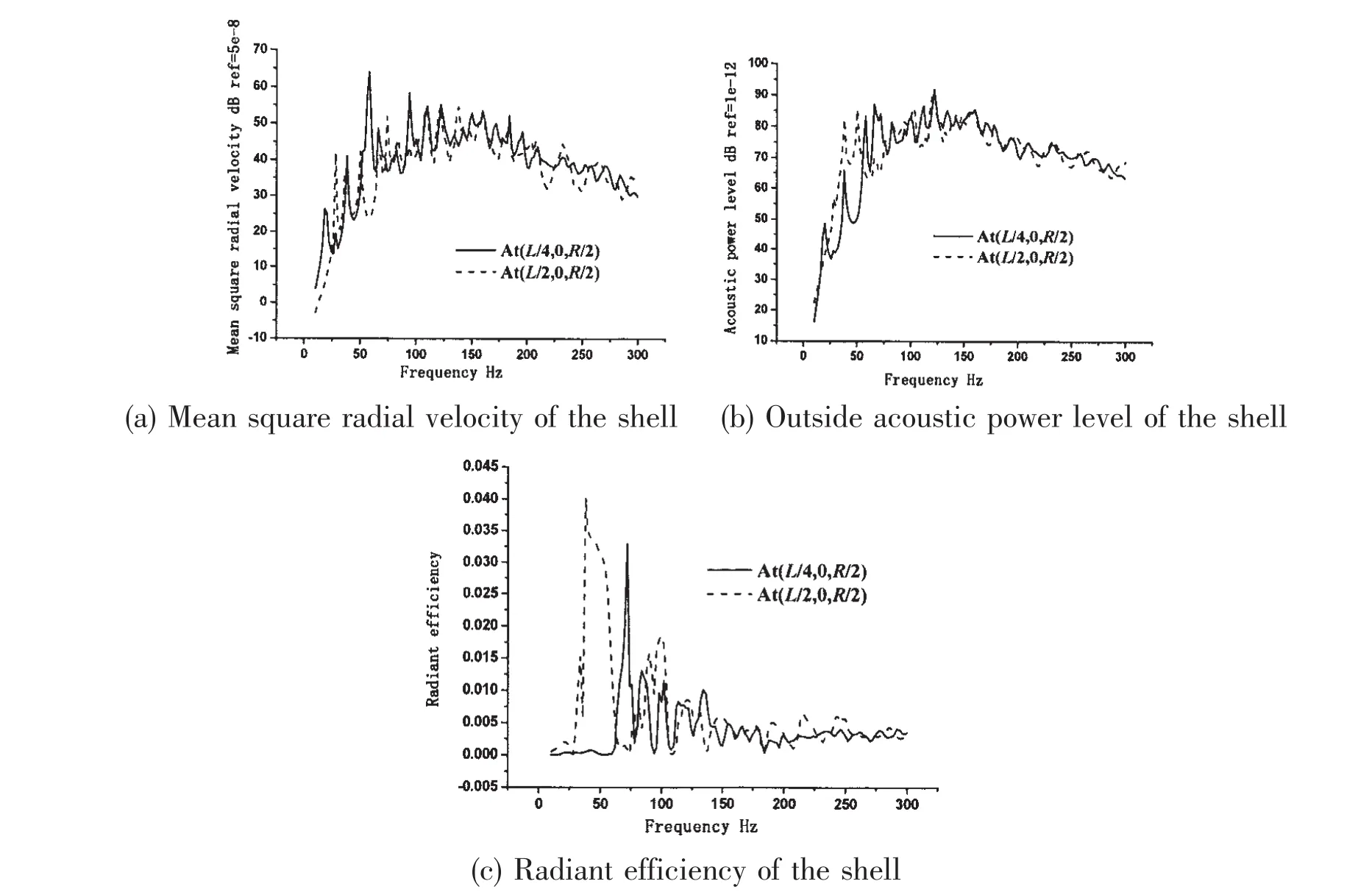
Fig.8 The shell excited by the internal point sound source with different axial positions

4.2 Vibro-acoustic characteristics of the cylinder excited by internal multi-sources

Two cases are discussed:one case is the shell containing two unit radial symmetrical internal sources with coordinatesrespectively,as shown in Fig.9(a).The other case is the shell containing two unit internal sources with coordinates（L/4,0,R/2）and（3/4L,0,R/2）respectively which are symmetric to the central section of the cylinder,as shown in Fig.9(b).

Fig.9 Two internal point sound sources in the cavity

(1)Two unit radial symmetrical point sound sources

Vibro-acoustic characteristics of the cylinder excited by two radial symmetrical unit sources with the same phases and opposite phases at the frequency range from 10～300 Hz are compared in Figs.10(a),(b)and(c).For f＜150 Hz,the maximal peak values of the mean square radial velocity and the acoustic power level of the cylinder excited by two sources with opposite phases are bigger than the case with same phases.And for f＞150 Hz,the effect of the sources’phases on vibro-acoustic characteristics of the cylinder is not notable.

Fig.10 The shell excited by two radial symmetrical unit point sound sources

Fig.11 Directivity patterns of the outside surface of the shell at x=L/2 excited by two unit radial symmetrical sources

Directivity patterns at x=L/2 of the outside surface pressure of the shell cylinder at 30 Hz and 100 Hz are given in Fig.11.Except that the angles of-π/2 and π/2,the difference of the outside surface pressure in the two cases is slight.

(2)Two unit point sound sources which are symmetric to the central section of the cylinder

Vibro-acoustic characteristics of the cylinder excited by two unit point sound sources which are symmetric to the central section of the cylinder at the frequency range from 10～300 Hz are compared in Figs.12(a),(b)and(c).For f＜75 Hz,the values of the curves in the case of opposite phases are clearly bigger than the case of same phases.For f=58 Hz,the mean square radial velocity difference between the two cases can achieve 70 dB,and the outside acoustic power level difference can achieve 40 dB.The Fig.12(c)shows that at one or two frequencies, the values of radiant efficiencies are very high in the case of opposite phases.

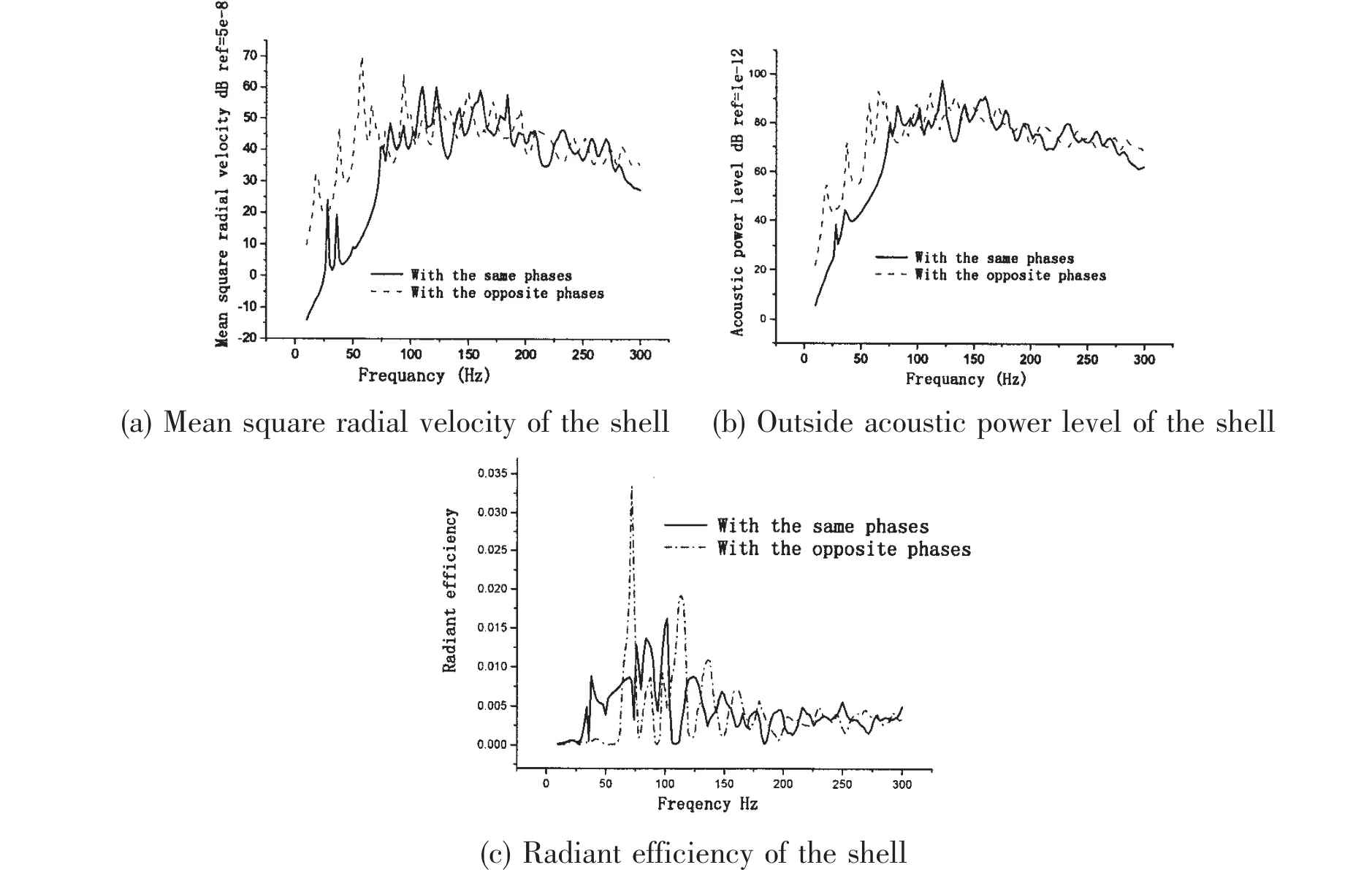
Fig.12 The shell excited by two unit sources which are symmetric to the central section of the cylinder

5 Conclusions

According to Flügge theory,the Helmholtz equation and a previous method for calculating the sound radiation of machines in an enclosure finite cylindrical shell,which produces both internal noise and forces,have been introduced.The effect of the cut-off mode orders of the cavity on the calculation accuracy is described.Then the influences of different positions of the interior source on acoustic of the stiffened cylindrical shell are obtained,and the comparisons of sound radiation properties of interior sources which have the same phases and different phases are carried out.The results of the present study are summarized as follows:

(1)The structure-cavity shows cluster coupling behavior.The structure modes of the shell selectively couple with some acoustic modes of the cavity.

(2)The effect of the longitudinal mode order n¯1of the cavity on the calculation accuracy is greater than n¯2and n¯3.Deservedly with the frequency increases the cut-off mode orders of the shell and the cavity must increase jointly to satisfy the calculation accuracy.

(3)The influence of the positions of the internal point sound source on the acoustic power level of the shell is small.The influence of the radial positions on the mean square radial velocity of the shell is greater than that of the axial positions,and with the frequency increases the influence gradually decreases.

(4)The influence of the phases of the two radial symmetrical unit sources on the vibroacoustic characteristics of the cylinder is smaller than that of the phases of two axial unit sources which are symmetric to the central section of the cylinder.But also with the frequency increases,the influence gradually decreases.

The discussion is favorable for noise reduction of submerged stiffened cylindrical shells.

[1]Laulagnet B,Guyader J L.Modal analysis of a shell’s acoustic radiation in light and heavy fluids[J].J Sound Vib,1989, 131(3):397-415.

[2]Laulagnet B,Guyader J L.Sound radiation by finite cylindrical ring stiffened shells[J].J Sound Vib,1990,138(2):173-191.

[3]Dowell E H,Gorman G F,Smith D.A.Acoustoelasticity:General theory,acoustic natural modes and forced response to sinusoidal excitation,including comparisons with experiment[J].J Sound Vib,1977,52(4):519-542.

[4]Nelson P A,Curtis A R D,Elliott S J,Bullmore A J.The active minimization of harmonic enclosed sound fields,part I: Theory[J].J Sound and Vib,1987,117(1):1-13.

[5]Chen Ke’an,Ma Yuanliang,Sun Jingcai.Active noise control within enclosed space surrounded by flexible structure[J]. Acta Acoustic,1994,19(6):434-443.

[6]Chen Meixia,Luo DongPing,Chen Xianing.Analysis of sound radiation characteristics of complex double shells[J].Acta Acoustic,2004,29(3):209-215.

[7]Luo Dongping,Zhang Yuhong.Analysis of vibratical characteristics of ring-stiffened cylindrical shells[J].Ship Building of China,1989(1):64-74.

[8]Junger M C,Feit D.Sound,structures and their interaction[M].MIT,Combrige,MA,1986.

[9]Flügge W.Stresses in shells[M].Berlin:Springer,1960.

[10]Frank Fahy.Sound and structural vibration:Radiation,transmission and response[M].Academic Press,London,1985.

[11]Morse P M.Theoretical acoustics[M].New York:Mc Graw-Hill,1968.

TB53 U661.44Document code:A

10.3969/j.issn.1007-7294.2014.03.011

1007-7294（2014）03-0328-16

date：2013-11-18

Biography：GUAN Shan-shan(1982-),female,engineer of Wuhan Secondly Research Institite of Ship-designing, E-mail:saraguan@163.com;DENG Hai-hua(1979-),senior engineer.