隧道控制线性转换法代替交切投点法研究
2014-06-06陈泽远
陈泽远
(中铁第一勘察设计院集团有限公司,陕西西安 710043)
0 引言
为控制隧道贯通误差,需根据隧道长度、形状及贯通面位置做专门隧道控制网优化设计。传统隧道控制测量时需利用既有控制点进行设计线条交切点的投放,交切投点测量纳入隧道控制网,根据交切点坐标确定交点、偏角等线性要素,建立施工独立坐标系,传统交切投点法步骤繁琐、工作量大。线性转换法省略交切点投放及联测环节,直接利用既有控制点转换设计线条要素,工作量小、精度高,不改变线路设计资料,操作简便。
1 隧道洞外平面控制测量现状
当线路平面控制网精度不能满足隧道平面控制测量要求时,应建立隧道洞外平面控制网,隧道洞外平面控制网结合隧道长度、平面形状、辅助坑道位置以及线路通过地区和环境条件等,一般采取GPS测量方式。为有效控制长度综合变形以及便于隧道施工,隧道平面控制网需建立施工独立坐标系,施工独立坐标系宜采用以隧道平均高程面为基准面,取隧道工程中心经线作为坐标投影的中央子午线,以隧道长直线或曲线隧道切线为坐标轴。
隧道洞外平面控制测量依据规范规定的隧道洞外平面控制测量贯通误差进行洞外控制网设计,采取GPS静态测量方式,隧道洞外平面控制点、既有控制点及交切投点均纳入GPS控制网中。交切投点是设计线路中线或切线上的点,利用全站仪或GPS RTK技术进行实地放样,实地控制线路位置及走向。目前隧道洞外控制仍利用交切投点方式实地控制线路位置及走向,每条直线边要求投点2个,位于线路中线或切线上。首先根据隧道线性资料和测区地形确定交切投点位置,如投点位置附近没有既有控制点,需进行控制点同精度拓展,在既有控制点或同精度拓展的控制点的基础上,利用全站仪极坐标法进行交切投点。交切投点纳入到整个隧道GPS控制网中进行观测,数据处理满足精度要求后计算验后横向贯通中误差,验后横向贯通中误差满足规范要求后建立隧道施工独立坐标系,同时得到交切投点的施工独立坐标系坐标。交切投点延长相交得到新交点坐标,在保证原隧道线路设计资料曲线要素中缓和曲线和半径不变的前提下,计算新线性资料,比较新旧线条偏角、曲线长度,结合设计专业确定最终新线性资料、新旧里程对照表及各中线控制桩坐标。
目前交切投点法由于投点存在偏差,致使新线性资料与设计线性有较大偏差,需修改线路设计资料。工程实例交切投点法偏角较差统计见表1。
2 线性转换法原理
2.1 平面相似坐标转换模型
两个不同平面坐标系的坐标可采取坐标变换模型实现坐标转换。平面坐标转换一般采取四参数的相似坐标变换,包含两个平移参数、一个旋转参数和一个尺度参数,要求由不少于两个公共点坐标利用最小二乘法计算四参数即实现不同坐标系间的坐标转换。平面四参数坐标转换原理如下:
设两坐标系之间的夹角为α,平移距离为A0,B0,两坐标系之间坐标的比例因子为m,则:
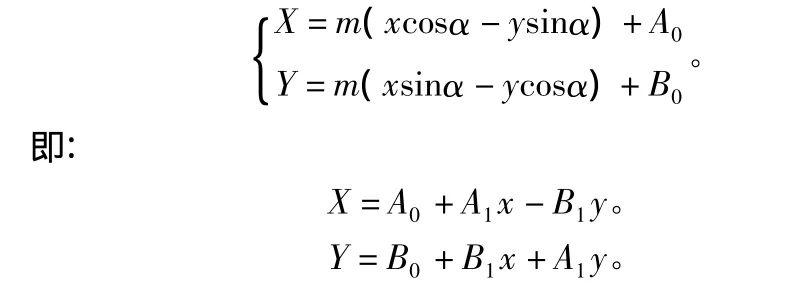
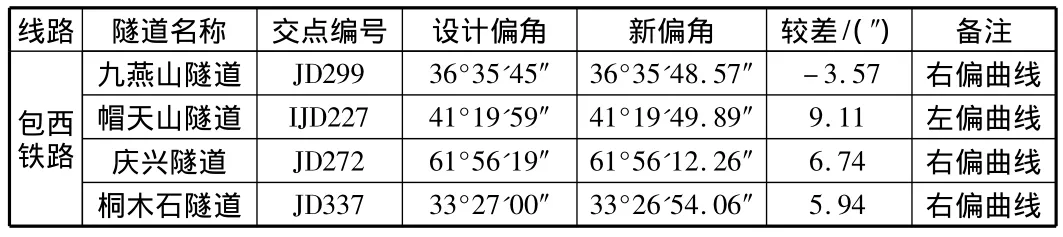
表1 交切投点法偏角较差统计表
设Vx和Vy分别为同一点两坐标系变换产生的坐标误差,即:
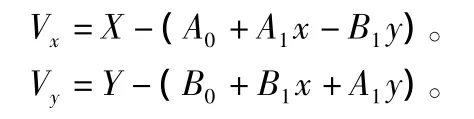
2.2 线性资料坐标转换研究
线性资料由里程、线性坐标及曲线要素组成,曲线要素主要包括曲线偏角、曲线半径和缓和曲线长,线性坐标包含起点坐标、交点坐标、终点坐标、进口坐标和出口坐标等。
不同平面坐标系的坐标可通过相似坐标变换实现坐标转换。隧道洞外控制网观测时纳入既有控制点,建立施工独立坐标系后既有控制点拥有原坐标系下和施工独立坐标系下的平面坐标,理论研究可利用既有控制点不同坐标系下的平面坐标把线性坐标转换到施工独立坐标系中,保持隧道线路曲线要素中的曲线半径、缓和曲线长不变,生成施工独立坐标系下的隧道线路资料,以此为依据进行施工测量。线性转换法无投点误差,仅仅利用既有控制点进行坐标相似转换,不改变设计资料,工程实例线性转换法偏角较差统计见表2。
2.3 线性转换法和交切投点法理论分析
交切投点法是利用既有控制点把交切实地投点,纳入隧道控制网观测,得到施工独立坐标系坐标,交切投点延长相交得到交点在施工独立坐标系中的坐标,保持曲线半径、缓和曲线长度不变生成新线性资料;线性转换是省略实地交切投点,利用既有控制点不同坐标系下的坐标把线性坐标转换到施工独立坐标系中,保持隧道线路曲线要素中的曲线半径、缓和曲线长不变,生成施工独立坐标系下的隧道线路资料。两种方法均能实现施工独立坐标系下的新线性资料的生成,均能用于隧道贯通测量,但交切投点法由于投点偏差、联测误差的影响会改变设计偏角,从而导致设计资料的改变。

表2 线性转换法偏角较差统计
以5 km直线边为例,统计偏角改变下造成的设计线位横向最大偏差,统计见表3。

表3 偏角改变对横向偏差的影响
隧道途经区域植被茂密、山高坡陡,交切投点是隧道洞外业控制测量中最艰难的环节,交切投点一般投放在沟壑之中,GPS测量难度极大。线性转换法省略既有控制点同精度拓展及交切投点,优势明显,主要体现在:
1)线性转换法无投点误差,精度高,未改变偏角、不改变设计资料;2)线性转换法省略既有控制点同精度拓展及交切投点,工作量锐减,节约成本;3)线性转换法降低隧道洞外控制测量难度,实用性更强。
3 线性转换法工程应用实例
云桂铁路六郎山隧道位于红石岩—南盘江区间,全长14 090 m;六郎山隧道和对门山隧道相邻,两隧道之间为牛家坪大桥,六郎山隧道进口进洞为直线,出口为曲线(见图1)。

图1 六郎山、对门山隧道示意图
六郎山隧道进出口、横洞和斜井附近均有CPI平面控制点,点号分别为 CPI267B,CPI268B,CPI267-1,CPI268-1,CPI269,CPI控制点达到二等GPS技术要求,依据TB 10601-2009高速铁路工程测量规范,原CPI点位选取及精度均无法满足隧道控制的要求,应采用一等GPS控制网,因此六郎山隧道需建立隧道独立平面控制网。
3.1 隧道洞外平面控制网建立
每端洞口、斜井和横洞布设GPS控制点不少于3个,至少保证两点间通视;原CPI控制点纳入整个隧道洞外平面控制网中,制定观测计划,采用标称精度为5 mm+1 ppm×D(D为距离,以km计)的Trimble双频GPS R8接收机、按一等GPS技术要求进行施测;利用徕卡Geo Office Combined7.0软件进行数据处理、基线解算;利用科傻GPS数据处理软件在WGS84坐标系统下进行无约束平差,得到各点WGS84坐标系下空间直角坐标。
3.2 施工坐标系的建立
为控制长度综合变形,综合考虑各特征点和隧道平面控制点的大地坐标和大地高,确定工程坐标系中央子午线为103°42'、投影面大地高为1 410 m;利用同济大学GeoTrans软件把各控制点空间直角坐标投影到相应的高斯平面上,得到各点高斯平面坐标;根据既有CPI控制点不同坐标系下的坐标,把线性坐标利用相似坐标转换原理转换到施工坐标系中;新线条起点选在DK573+600(直线路基)、终点选在DK587+900(曲线路基);保持曲线缓和曲线长度、曲线半径要素不变,根据起点里程,起点、各交点和终点坐标重新生成线条,比较新旧曲线偏角、切线长和曲线长等资料。新旧曲线要素比较表见表4。

表4 新旧曲线要素比较表
3.3 施工独立坐标系的建立
以新线条DK574+000,DK577+000所在直线段大里程方向为X轴方向,以垂直于X轴满足右手定则直线为Y轴方向,假定DK574+000的坐标为(574 000,10 000),建立施工独立坐标系;把各GPS控制点、进出口点、横洞斜井点、各交点坐标转换到隧道施工独立坐标系;根据施工独立坐标系下各点坐标及曲线要素,重新生成施工独立坐标系下线条,作为指导隧道施工测量的依据。
3.4 横向贯通误差精度预计
隧道洞外测量控制网是隧道施工测量的基础,直接影响隧道贯通的精度,隧道控制网施工采取两端掘进、中间贯通的方式,贯通里程为 K580+838,该点坐标为 X=580 675.712 6,Y=10 880.242 5,贯通面方位角αF=121°28'40″,隧道贯通面见图2,进口端、出口端控制点点位中误差统计见表5。

图2 隧道贯通面示意图

表5 控制点点位中误差统计 mm
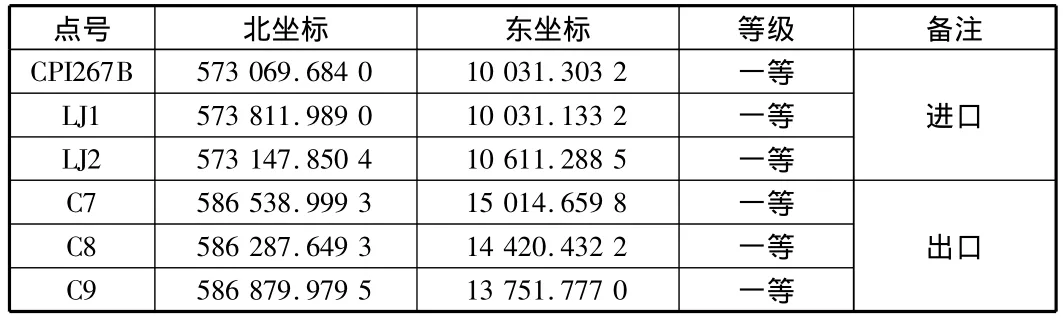
表6 隧道洞外控制点成果 m
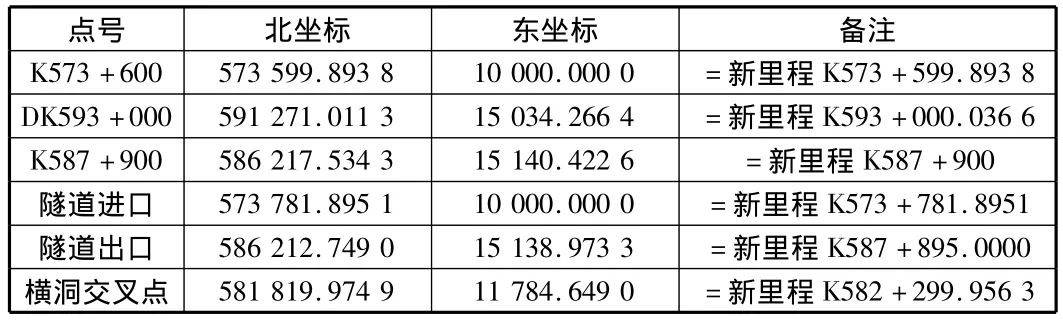
表7 新线性坐标成果 m
隧道洞外控制测量的验后横向贯通中误差按下式计算:
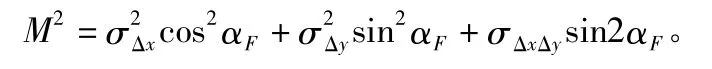
其中,σΔx,σΔy,σΔxΔy分别为由进、出口推算至贯通点的 x,y 坐标差的方差和协方差;αF为贯通面方位角。
把以上各项代入公式,得出M=28.4 mm<65 mm,因此本次隧道外平面控制测量满足隧道贯通洞外控制点的精度要求。
3.5 隧道控制测量成果
隧道洞外控制点成果见表6,新线性坐标成果见表7。
4 结语
在隧道洞外控制测量中线性转换法优于交切投点法,线性转换法不需要既有控制点的同精度拓展,也不需要交切投点,精度高,未改变偏角、不改变设计资料;减少了工作量、提高了工作效率;降低隧道洞外控制测量难度,实用性更强。
[1]TB 10601-2009,高速铁路工程测量规范[S].
[2]TB 10054-2010,铁路工程卫星定位测量规范[S].
[3]张正禄,张松林.20~50 km超长隧道(洞)横向贯通误差允许值研究[J].测绘学报,2004,33(1):83-88.
[4]顾利亚.GPS隧道控制网横向贯通精度估算[J].西南交通大学学报,2004,39(1):25-29.
[5]丁冬夏.GPS控制网在长大隧道控制测量中的应用[J].交通科技,2006(2):33-35.
[6]刘国雄.GPS控制网在铁路隧道中的应用[J].石家庄铁道学院学报,2004(5):100-103.
[7]陈泽远.GPS交切技术在隧道地区测设中的应用[J].铁道勘察,2008(6):33-35.
[8]陈廷武,段红志.坐标相似变换模型的探讨[J].北京测绘,2008(4):18-19.
[9]姚清华.浅谈平面坐标转换[J].江西测绘,2010(1):22-23.
[10]安 卫,闫学静.一种平面四参数坐标转换方法的实现[J].北京测绘,2012(5):53-55.
