面向任务的可重构模块化机器人构型设计

吴文强，管贻生，朱海飞，苏满佳，李怀珠，周雪峰

(1.华南理工大学 机械与汽车工程学院，510641 广州;2.广东工业大学机电工程学院，510006 广 州;3.广东省自动化研究所，510070 广州)

面向任务的可重构模块化机器人构型设计

吴文强1，管贻生2，朱海飞1，苏满佳1，李怀珠1，周雪峰3

(1.华南理工大学 机械与汽车工程学院，510641 广州;2.广东工业大学机电工程学院，510006 广 州;3.广东省自动化研究所，510070 广州)

为解决可重构模块化机器人在应用时如何找到合适的构型来满足特定任务的问题，提出一种面向任务的可重构模块化机器人构型多目标优化方法.讨论该模块化机器人系统的基本结构，包括主要的模块和控制系统的组成结构;在任务描述的基础上，给出模块化机器人构型设计的优化模型和流程;针对特定的攀爬任务和操作任务，对模块化机器人的构型进行优化设计.仿真验证了该方法的可行性和有效性.该方法具有面向任务和多目标优化等特点，涵盖了自由度、可达性、耗能等多方面的性能优化，适用于模块化机器人的构型设计.

面向任务;模块化;可重构机器人;构型设计;遗传算法

模块化技术已广泛应用于机器人领域的产品研究和开发中.可重构模块化机器人由于结构和功能的可重组性，相对传统机器人更具有柔性，对任务和环境的适应能力更强.采用模块化技术，方便机器人的维护和保养，同时大大减少了机器人结构设计的周期，降低了成本.

近年来，可重构模块化机器人的研究方向多集中在模块设计、构型设计、运动学和动力学模型、控制系统等几个方面［1］.构型设计一般是一个根据具体的任务从不同模块组合中选择最优构型的优化问题，这些模块多是事先设计好的、独立的机电系统，并且具有相同的软、硬件接口，例如卡内基梅隆大学的 RMMS［2］、德国宇航中心的LWR-Ⅲ［3］、美国 Robotics Research Corporation 的模块化机器人及德国Schunk公司的PowerCube和PRC系列模块等.优化模型的设计变量即是一个完整的机器人构型，可以表达成有向图［4］、关联矩阵(AIM矩阵)［5］等形式.其评价构型优劣的标准可以是最少自由度［6］、灵巧型［7］、容错性能［8］等单项指标，或者是多个性能指标的加权融合［9－10］.这些性能指标可看做优化模型的目标函数或者约束条件.建立运动学和动力学模型是分析这些性能指标的基础，通常采用如下两种方法:一是 Denavit-Hartenberg(D－H)法［11］，根据模块本身的参数和装配方式，自动生成机器人构型的D－H参数，从而建立机器人模型;另外一种是product-of-exponential(POE)法［12］，机器人模型可由构型中模块的结构参数直接生成.遗传算法(genetic algorithms，GA)是模块化机器人构型优化最常用的算法，文献［9］中用了一个双层GA算法进行优化，上层GA确定构型，下层GA计算逆解，而在文献［11］中下层GA则用来完成机器人的尺度优化.这些GA算法都是单目标优化算法.

本文在现有的模块化机器人平台［13］的基础上，实现了一种面向任务的多目标构型优化算法.介绍了模块化机器人平台，包括基本模块和系统组成结构，给出了构型优化设计模型，通过3种不同任务的构型设计实例来验证算法的可行性和有效性.

1 模块化机器人系统

1.1 基本模块

模块化机器人系统是由一套具有相同连接方式的模块构成，根据机械结构及功能的不同可分为关节模块、连杆模块、执行器模块、辅助功能模块等.如图1所示.

1)摆转关节模块(T模块):单自由度关节模块，关节轴与模块输入输出轴线垂直，关节模块的伺服驱动装置采用结构紧凑的驱动器和直流伺服电机，并采用霍尔传感器作为限位开关;

2)回转关节模块(I模块):单自由度关节模块，关节轴与模块输入输出轴线平行;

3)连杆模块:与I模块结构类似，但不具有驱动功能，可用于调整机器人尺度;

4)吸附模块(S模块):由3个呈正三角形分布的吸盘、真空泵、压力传感器及其他气动元件构成，并采用独立的控制器对传感器信号进行采集和处理;

5)轮/足模块(W模块):可用于轮式移动机器人或特殊步行机器人;

6)夹持器模块(G模块):驱动装置是电流驱动的盘式电机，V型槽的设计使得能夹持圆形、方形等多种物体.

以上模块之间的连接采用卡环加定位销的方式，可快速实现模块化机器人的重构.通过组合这些模块，可以得到多种不同构型的机器人，例如机械臂、攀爬机器人、步行机器人、轮式机器人等［13］.

图1 模块化机器人基本模块

1.2 系统功能

根据模块化、可重构、开放性等设计准则，采用PC作为主控制平台，通过CAN总线与各个模块进行通讯，构成开放式、分布式的控制架构.

图2所示为模块化机器人系统功能结构简图，人机界面模块负责整个系统的总体调度和资源管理功能，包括人机交互、通讯、文件系统、状态监控、信息融合等功能;对机器人的控制和操作指令可通过如下3种方式输入:通过人机界面直接输入，通过遥操作器输入和外部传感器反馈;任务控制模块对输入的任务进行初步的解析和规划，若是设计任务则由构型设计模块进行处理，运动任务则进行相应的运动规划和运动控制，值得注意的是，设计功能模块和运动功能模块是建立在统一的模块化机器人运动学和动力学模型的基础之上的;基于OpenGL的仿真模块能够直观地描述设计的构型或机器人运动的状况.

图2 模块化机器人系统功能结构

2 构型设计模型

2.1 任务描述

模块化机器人的构型设计是一个基于任务的设计过程.一般情况下，一个完整的任务可以分解成一系列的子任务，例如搬运任务可分解为检测、抓取、搬运、放置等，而在构型设计中，只需考虑与机器人运动相关的细节;因此，对于特定的任务，可表示为机器人在操作空间中的运动轨迹.文献［6］和文献［14］将机器人的工作任务描述为操作空间一系列零散的任务点，Tp={p∈SE(3)}，这些点仅表示位置或位姿信息，而没有给出时间相关信息，因此只能考虑可达性要求，而不包含动力学方面的要求.一个完整的任务描述应包含速度、加速度和力的信息:

式中任务Tp是由操作空间内一系列的位置向量p、速度向量v、加速度向量a和负载向量τ组成.

由于任务不同，这些任务点向量的维数可能少于6，例如，一个R3中的任务只有3个自由度，而机器人最终构型的自由度数则取决于具体的任务.

2.2 优化模型

通过组合不同的模块，可装配成多种不同运动学和动力学特征的机器人，构型设计的目的就是从中选择出最适合当前任务的装配形式.基于任务的模块化机器人构型优化设计模型同样包含设计变量、目标函数和约束条件3部分，具体描述如下:

式中:x为设计变量，f(x)为多目标函数向量.

2.2.1 设计变量

由于各个模块本身的参数已确定，在构型设计中，一个设计变量(机器人构型，即x)仅包括模块的种类、数量及模块之间的连接方式等.对于串联机器人，由于没有环结构，一个有向树就可以很形象地描述此构型;因此，一个设计变量最终可以描述为基于图论的关联矩阵的形式.

2.2.2 目标函数

目标函数f(x)用于评价每个机器人构型适应给定任务的优劣程度.机器人评价指标有很多种，单一目标很难客观地评价一个机器人构型的好坏程度，多目标的融合或优化策略是很必要的.在这里取f(x)=［fdoffergfvel］，这3个函数分别表示自由度指标、能量指标和运动学传递性能指标.

对于一个特定的任务，通常希望使用最少的模块，特别是与自由度紧密相关的关节模块，自由度指标可定义为

式中:ndof和nmdl分别表示自由度数目和模块数目，wn和wm为加权系数.

机器人能量消耗大致可分为两部分，机械能和损耗能，因此能量指标定义如下:

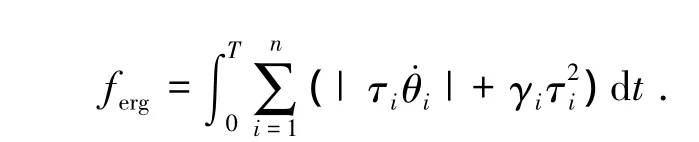
式中:γi是第i个关节的耗能系数，与驱动关节运动电机的速比、电枢电阻和转矩常数有关;T为执行任务总耗时;n为机器人自由度数;τi和˙θi分别是在t时刻第i个关节的转矩力和速度.

速度指标用于评价机器人在任务空间中传递性能，可用全局条件数［15］来表示:

式中kJ为任务空间W中当前位姿的机器人条件数.

2.2.3 约束条件

1)变量约束:变量的设计域约束Dcfg与具体的模块相关，例如夹持器等末端执行器模块只能装配在末端，两个相邻的关节模块不能同轴等，另外构型的自由度数目一般不超过7;

2)可达性约束:即是否存在逆解的问题，可描述为freach=‖Δ‖≤εp，其中，‖·‖表示欧氏距离，εp表示最大允许误差;

3)关节约束:包括关节位置Θ、速度V、加速度A和力/力矩约束Γ，iL和iU分别表示关节约束的最小和最大值，其中i=Θ，V，A，Γ.

2.3 优化流程

模块化机器人构型优化的流程如图3所示.

图3 模块化机器人构型优化流程

模块库和任务为输入量，优化结果为最优构型表达(多目标优化问题通常存在一个解集)，具体流程如下:首先，从模块库里选择适量的模块进行装配，对于符合变量设计域的装配体进行构型的自动生成，包括机器人构型参数的生成，运动学、动力学自动建模等;然后，根据目标函数和约束条件对此构型进行性能评价;重复以上步骤直到目标函数值满足预期或者达到了设定的迭代次数.

由于本文所研究的构型为串联结构，因此机器人运动学正解可由各个模块的参数和连接参数直接求得;运动学逆解可由Newton-Raphson迭代法求解;而动力学则可通过Newton-Euler递推公式求得.其中雅可比矩阵是运动学问题的基础，由于模块化机器人构型的多样性，雅可比矩阵一般不是方阵，求逆问题可用伪逆的方法:

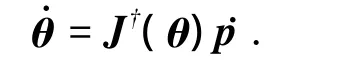
式中:λ为阻尼因子，I为单位矩阵.

3 实例

3.1 爬壁任务

爬壁机器人可以在墙壁或天花板上自由移动，因而能够替代人类从事墙壁清洁、核设施维护、船体喷涂、消防救援等高危任务，已逐渐成为机器人领域的研究热点.这里所研究的对象为双手爪式模块化机器人，机器人的两端是两个吸附模块，其他模块则根据具体的任务而定.

如图4所示为一个简单的爬壁任务，要求机器人在相邻两个墙壁上做壁面过渡运动.

图4 爬壁任务

设第一个吸附模块(记作S1)吸附在第一个墙面上，在其上建立的坐标系{B}为机器人的基坐标系，另外一个吸附模块S2从第一个墙面上的一个吸附点P1移动到另一个墙面上的一个吸附点P4，并要求S2分别在这两个墙面上的这两个点能够吸附成功，坐标系{T}为工具坐标系.可以看出，为了保证吸附模块在每个吸附点吸附成功，需要保证工具坐标系的z轴方向与吸附点所在墙面垂直，再加上3个位置量，因此这个任务是5维的.为了避免S2在移动过程中与墙壁相碰撞，假设P1和P2之间、P3和P4之间的轨迹姿态不变，这两段轨迹可以规划为直线，轨迹点数据可由下式求得:

式中:pt、vt和at分别为t时刻轨迹点的位姿、速度和加速度.而P2和P3之间可以规划为点到点(PTP)或直线等轨迹形式，且姿态不需要保证.

爬壁机器人属于移动机器人的一种，当S2移动到目标位置并吸附墙2，而后松开S1，并移动至墙2上的一个目标位置并吸附，从而可实现一个完整的壁面过渡运动.为体现双手爪移动的特性，把优化模型(1)中的目标函数修改为

式中:x-1表示反向装配的机器人构型，若x是初始条件下S1吸附固定、S2移动的构型，则x-1就是使S2固定、S1移动的构型.

这里采用NSGA-II(non-dominated sorting in genetic algorithm II)［16］来实现构型设计的多目标优化问题.NSGA-II算法是在NSGA的基础上引入快速非劣排序方法，降低了计算复杂度;并引入密度估计操作算子作为新的多样性保持策略;同时引入精英保留机制，使得NSGA-II具有非常好的多目标优化性能.

NSGA-II提供两种编码方式:实数编码和二进制编码.本文采用了二进制编码方式，如图5所示为NSGA-II二进制编码的一个示例，其中仅包含了各个模块的类型及装配模式.

图5 NSGA-II编码示例

主要参数设置如下:交叉概率为0.8，变异概率为0.05，种群数设为50;式(2)中的加权系数wn和wm分别设置为0.6和0.4.经过50次进化之后得到了4组可行的构型，如图6所示，f1、f2和f3分别表示自由度指标、能量指标和运动学指标的值，其中(a)、(b)和(d)为5自由度构型，(c)为6自由度构型，这些构型都是Pareto最优解.在应用时，可以从该最优解集中选择一个更适合当前任务和环境的最优解.可以看出，(b)具有最少的模块数，但为了完成运动任务所消耗的能量比较大;(c)模块数较多，但耗能比较少;(d)具有较少的自由度和明显的对称结构，在爬壁控制时会带来很多便利，因此在执行爬壁任务时可优先选用(d)构型的机器人，并命名为 W-Climbot［17］.

图6 爬壁机器人构型优化结果

3.2 爬杆任务

爬杆机器人可用于摘果子、修剪枝叶、检修桥梁、维护路灯等高空作业，对双手爪式模块化攀爬机器人的相关研究可参考文献［13，18］，本节则是将上述的设计方法应用于爬杆作业.

一个简单的爬杆任务如图7所示，要求机器人在空间两个杆之间做攀爬运动，设第一个手爪G1抓紧第一个杆，在其上建立的坐标系{B}为机器人的基坐标系，另外一个手爪G2沿着第二杆从一个点P1移动到另一个点P2，假设运动轨迹为一条直线.为了能够准确抓持圆杆，需要保证x方向的姿态，因此这个任务也是5维的.优化算法同样采用NSGA-II，其参数设置同上.

图7 爬杆任务

经50次进化后得到6组不同的构型(如图8).

图8 爬杆机器人构型优化结果

图8中(a)、(b)和(d)为5自由度构型，另外3个为6自由度构型.可以看出，(b)与爬壁机器人构型优化结果中的(d)具有相似的构型，具有较少的自由度和明显的对称结构，当爬杆任务的维数不超过 5 时，优先选取此构型，并称之为 Climbot［18－19］.

3.3 操作任务

工业机器人是目前最成熟、应用最广泛的一类机器人，在焊接、搬运、喷涂、装配等很多行业都有典型的应用.但传统工业机器人的构型不可改变，当给定任务复杂多变时，由于本身机械构型的限制，可能难以满足需求.模块化方法则可以很好地解决这个问题，扩大了工业机器人的应用范围.

如图9为一个简单的操作任务，机器人把一个物体从一个点P1搬运到另一个点P2.由于不涉及姿态，这个任务是3维的，同样假设这两点之间的运动轨迹为直线.优化算法及参数设置同上.

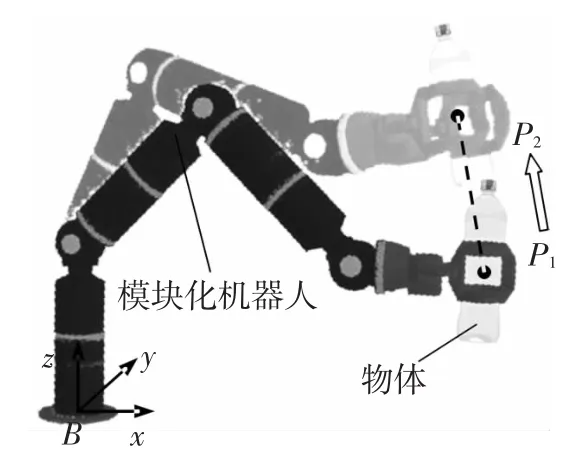
图9 操作任务

经50次进化后得到8组不同的构型(如图10)，其中(a)～(e)为3自由度构型，(f)～(h)为4自由度构型.可以看出，较少自由度的构型传递性能较差，并且在完成给定的运动任务时，所消耗的能量也较大，而4自由度构型则具有较好的传递性能和较少的耗能.对于当前3维的任务，4自由度构型为冗余构型，在这种情况下，运动学逆解可能有无数组解，可以用优化方法求解，本文采用统一的逆解迭代式(3)来求取其最小二乘解.

图10 操作机器人构型优化结果

为形象地描述模块化机器人的组成结构，以图10(b)构型为例，建立其仿真模型如图11，此构型机器人由基座和另外5个模块组成，其中包含2个T关节模块、1个I关节模块、1个连杆模块和1个夹持器模块，各模块之间采用卡环连接.

图11 3－DoF构型仿真模型

4 结论

1)本文提出了一种面向任务的可重构模块化机器人构型设计方法，该方法能够根据现有的模块和特定的任务，得到一组满足多目标函数优化的最优构型.

2)该方法采用多目标优化模型，体现了自由度、可达性、能耗、运动学传递等多方面的性能优化.针对攀爬任务和操作任务的仿真实例很好地验证该方法的可行性和有效性.

3)在给定步行任务的情况下，该方法同样适用于以轮/足模块作为双足的模块化主动步行机器人构型的分析与设计.

［1］刘明尧，谈大龙，李斌.可重构模块化机器人现状和发展［J］.机器人，2001，23(3):275－279.

［2］PAREDIS C J J，BROWN H B，KHOSLA P K.Rapidly deployable manipulator system ［J］. Roboticsand Autonomous Systems，1997，21(3):289－304.

［3］ALBU－SCHAFFER A，EIBERGER O，GREBENSTEIN M，et al.Soft robotics ［J］.IEEE Robotics and Automation Magazine，2008，15(3):20－30.

［4］CASTANO A，WILL P.Representing and discovering the configuration of Conro robots［C］//IEEE InternationalConference on IntelligentRobotsand Automation.Piscataway:IEEE，2001:3503－3509.

［5］CHEN I M，BURDICK J.Enumerating the non-isomorphic assembly configurations of modular robotic systems［J］.International Journal of Robotics Research，1998，17(7):702－719.

［6］YANG G，CHEN I M.Task-based optimization of modular robot configurations:minimized degree-of-freedom approach［J］.Mechanism and Machine Theory，2000，35(4):517－540.

［7］YIM M，DUFF D G，ROUFAS K D.PolyBot:a modular reconfigurable robot［C］//IEEE International Conference on Robotics and Automation.Piscataway:IEEE，2000:514－520.

［8］LI Q，ZHAO J.A universal approach for configuration synthesis of reconfigurable robots based on fault tolerant indices［J］.Industrial Robot，2012，39(1):69－78.

［9］CHOCRON O，BIDAUD P.Evolutionary algorithms in kinematic design ofrobotic systems［C］//IEEE InternationalConference on IntelligentRobotsand Systems.Piscataway:IEEE，1997:1111－1117.

［10］FARRITOR S，DUBOWSKY S.On modular design of field robotic system［J］.Autonomous Robots，2001，10(1):57－65.

［11］HAN J，CHUNG W K，YOUM Y，et al.Task based design of modular robot manipulator using efficient genetic algorithm［C］//IEEE International Conference on Robotics and Automation.Piscataway:IEEE，1997:507－512.

［12］BI Z M，ZHANG W J，CHEN I M，et al.Automated generation of the DH parameters for configuration design of modular manipulators［J］.Robotics and computer-Integrated Manufacturing，2007，23:553－562.

［13］GUAN Y，JIANG L，ZHANG X，et al，Development of novel robots with modular methodology［C］//IEEE/RSJ InternationalConference on IntelligentRobotsand Systems.Piscataway:IEEE，2009:2385－2390.

［14］CHEN I M，BURDICK J.Determining task optimal modular robotassembly configurations［C］//IEEE International Conference on Robotics and Automation.Piscataway:IEEE，1995:132－137.

［15］ANGELES J，LOPEZ－CAJUN C S.Dexterity index of serial－type robotic manipulators［C］//American Society of Mechanical Engineers，Design Engineering Division(Publication)DE.New York:ASME，1988:79－84.

［16］DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multi-objective genetic algorithm:NSGA－II［J］.IEEE Transactions on Evolutionary Computation，2002，6(2):182－197.

［17］GUAN Yisheng，ZHU Haifei，WU Wenqiang，et al.A modular biped wall-climbing robot with high mobility and manipulating function［J］.IEEE/ASME Transactions on Mechatronics，2013，18(6):1787－1798.

［18］江励，管贻生，蔡传武，等.仿生攀爬机器人的步态分析［J］.机械工程学报，2010，46(15):17－22.

［19］GUAN Y，JIANG L，ZHU H，et al.Climbot:A modular bio-inspired biped climbing robot［C］//IEEE InternationalConference on IntelligentRobotsand Systems.Piscataway:IEEE，2011:1473－1478.

Task-oriented configuration design of reconfigurable modular robots

WU Wenqiang1，GUAN Yisheng2，ZHU Haifei1，SU Manjia1，LI Huaizhu1，ZHOU Xuefeng3

(1.School of Mechanical and Automotive Engineering，South China University of Technology，510641 Guangzhou，China;2.School of Mechanical and Electrical Engineering，Guangdong University of Technology，510006 Guangzhou，China;3.Guangdong Institute of Automation，510070 Guangzhou，China)

For solving the problem of finding suitable robot configurations to meet the specific tasks in the application of reconfigurable modular robot，a task-oriented multi-objective configuration optimization method is discussed.At beginning，the basic structure of the modular robot system is introduced，including the main modules and components of the control system.Then，based on the description of the task，an optimization model of modular robot configuration design is represented.Finally，for the specific tasks of climbing and manipulating，the configuration optimal design of modular robot is processed.The feasibility and effectiveness of the method have been well verified by the optimization simulation.The method is task-oriented and multiobjective， and it includes the performance optimization of degrees-of-freedom， reach-ability， energy consumption，and so on.

task-oriented;modular;reconfigurable robot;configuration design;genetic algorithm

TP242

A

0367－6234(2014)03－0093－06

2013－05－22.

国家自然科学基金资助项目(50975089);广东省自然科学基金资助资助(S2013020012797).

吴文强(1983—)，男，博士研究生.

管贻生，ysguan@scut.edu.cn.

(编辑 杨 波)