基于物理模型的动态海面电磁仿真方法研究
2014-06-05周斌刘恩晓杨雷梁志恒陶青长
周斌,刘恩晓,杨雷,梁志恒,陶青长
(1.山东省科学院海洋仪器仪表研究所,山东 青岛 266001;2.清华大学精密仪器系,北京 100084)
基于物理模型的动态海面电磁仿真方法研究
周斌1,刘恩晓1,杨雷1,梁志恒2,陶青长2
(1.山东省科学院海洋仪器仪表研究所,山东 青岛 266001;2.清华大学精密仪器系,北京 100084)
针对微波海洋遥感中复杂海面电磁环境难以准确建模的问题,给出了粗糙海面及目标的电磁仿真方法。通过海浪谱模型建立了与实际情况相符的三维海面,设置相应的电磁参数,准确复现海洋环境。采用时域有限差分方法(FDTD),将空间和时间离散化并进行迭代运算,计算动态实时的电磁分布状态。最后通过仿真对海面模型进行验证,并给出了相应的电磁分布状态。结果表明,该方法能够有效实现完整的海洋电磁散射仿真系统。
微波海洋遥感;粗糙海面;电磁散射;时域有限差分方法
微波遥感是探测和跟踪海面目标的有效手段之一,广泛应用于海洋遥感领域。模拟海面的电磁散射首先需要了解探海雷达的工作原理,海洋微波遥感雷达的工作过程如图1所示,该示意图给出了从雷达发射信号到接收信号的整个过程。因为海洋电磁环境复杂多变,海面目标的回波信号往往淹没在强烈的海杂波中[1],严重影响雷达的工作效能。精确模拟出海面电磁环境能够有效地分析海杂波和目标回波特性,有利于研制高效的对海微波遥感系统。
构造海面模型的早期研究大多是通过对海浪谱模型反演获得的,如Neumann谱[2]、Phillips谱[3]、Pierson-Moskowitz谱[4]、Fung&Lee谱及JONSWAP谱[5]等。这些经验模型都是通过对海上实验数据的拟合得到的,其模型结果与实际情况相差很大,且并不具有动态性。
目前对粗糙海面电磁散射的研究方法主要可分为两类,一类是采用一定物理近似的解析方法,包括基尔霍夫近似(Kirchhoff Approximation,KA)[6](也称物理光学法(Physical Optics,PO))、双尺度方法(Two Scale Method,TSM)[7]和微扰法(Small Perturbation Method,SPM)[8]等。另一类是不做物理近似直接用数值方法求解的数值法,其中比较具有代表性的包括时域有限差分方法(Finite Difference Time Domain Method,FDTD)[9]和矩量法(Moment Method,MM)(或称为MOM(Method of Moment))。解析近似的方法物理过程简单,计算量小,但大多只局限于单次散射,无法考虑电磁波的多径传播、目标面元间的电磁耦合作用以及边缘绕射等复杂电磁过程,其计算精度与实际海面相比仍然具有很大的偏差,而数值方法很好地解决了这一问题。
本文针对海洋环境的动态特性,首先研究了海浪谱模型的动态海面模型的建模方法,并在此模型上加载电磁波,建立与真实海洋电磁特征相符的模型,然后采用FDTD算法对电磁散射特性进行计算,最后对海面和电磁分布进行了仿真。

图1 动态海面微波遥感工作状态示意图Fig.1 Illustration ofmicrowave remote sensing of dynamic ocean surface
1 电磁仿真方法
图2给出了与图1相对应的海面及目标电磁仿真系统的设计结构。首先建立三维动态粗糙海平面模型,模拟不同气象环境的海浪并设定海面电磁参数,在此基础上加载电磁场波,并划分远近场、设置边界条件,然后经FDTD模型对海面电磁分布进行计算,其中边界条件的确定和FDTD的计算是本系统的关键技术难点。

图2 电磁仿真系统设计结构图Fig.2 Block diagram of electromagnetic simulation system design
1.1 粗糙动态海面建模
1.1.1 海浪模型典型参数
1.1.1.1 均方根高度
均方根高度σ作为海面起伏变化过程中海面高度对于均值的偏离程度的度量,能够量化地反映海面粗糙程度[10]。高度起伏的均值定义为
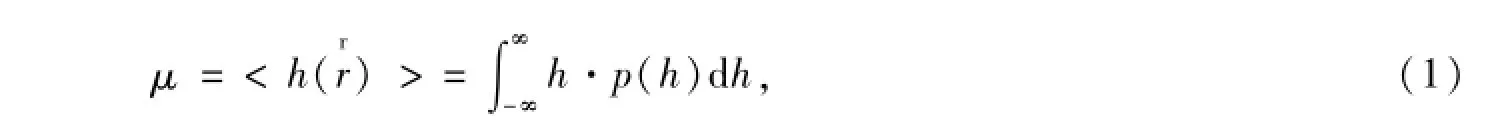
三维粗糙面为二元曲面函数,其显式表达式为:z=f(x,y),对应的概率密度函数g(x,y)则反映了粗糙表面轮廓的分布情况。作为一个描述随机特性的基本物理量,粗糙表面的均方根高度可根据表面概率分布函数定义为
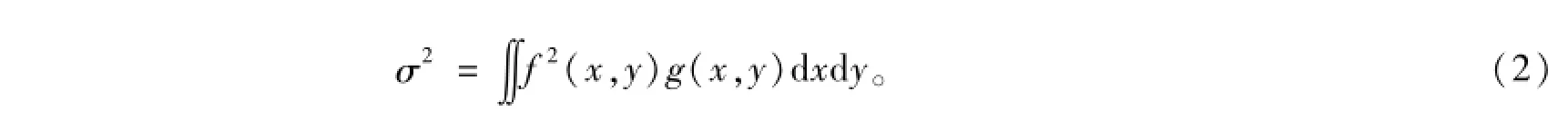
1.1.1.2 相关长度
相关长度反映了对于特定分布的粗糙海面上任意两点的关联程度,由自相关函数计算得到。粗糙海面的自相关函数定义为

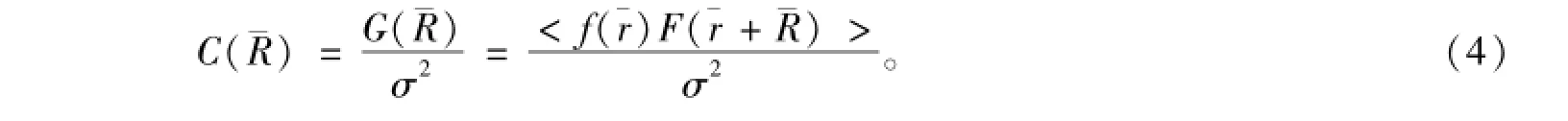
自相关函数值的分布与粗糙面的形状有关,而自相关函数的变化速度由粗糙面上不相关两点的距离决定。C(R)降至1/e时的R值称为表面相关长度,记为l,即C(l)=1/e,作为估计随机粗糙面上两点是否独立的评判基准,当二者水平距离大于l时,则认为这两点的高度分布是统计独立的。
对于三维粗糙面,随机表面上任意两点的自相关函数定义为
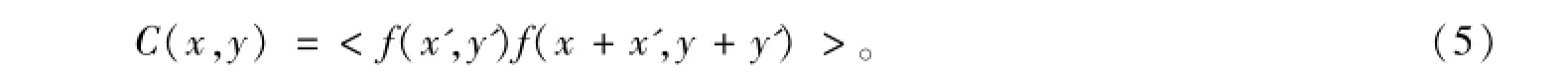
把C(x,y)的幅度在x,y方向上下降到1/e时的值称为粗糙面的相关长度,记为lx,ly。
1.1.1.3 功率谱密度
通过计算自相关函数的功率谱密度函数,可以表征粗糙表面的各谐波分量相对于空间波数的分布。
对于广义平稳的随机三维海面,粗糙表面起伏的自相关函数C(x,y)与其功率谱密度W(Kx,Ky)是一对傅里叶变换对,其起伏相关函数是随机过程的二阶统计特性之一[11],分别定义为
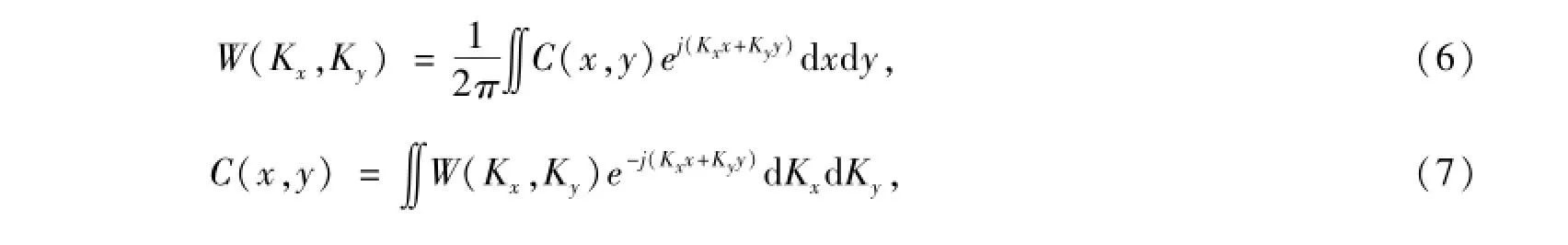
式中,Kx,Ky为几何空间波数。
1.1.2 动态海浪谱模型
选取合适的海浪谱模型,对风速、风向、海浪波长及海面大小等参数进行设置,通过傅里叶反变换即可得到时域的真实海面模型。本文采用Phillips谱函数作为海浪谱模型[12],即

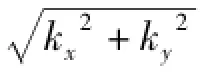
在进行Phillips海浪谱构建时,首先对仿真数据进行初始化,可以分为两个步骤进行[13]:
首先,给出原始的谱模型

其中ξr和ξi表示两个服从正态分布的均值为0,方差为1的随机变量。
其次,引入时间增量t,得到随机波面位移的计算公式

ω表示海浪移动方向上速度的随机量,ω与风向矢量K有如下关系

利用傅里叶反变换将式(10)代入下式

即可得到某一时刻的粗糙面位移。时间间隔的量化程度控制着海浪的变化速度,即海浪起伏的快慢,风速则决定了海浪起伏的幅度,而风向为海浪的洋流方向。式中X为空间固定点的位置向量;t为时间变量。h(X,t)为波面位移。在这里k为风向矢量K的模,因此K可以表示为
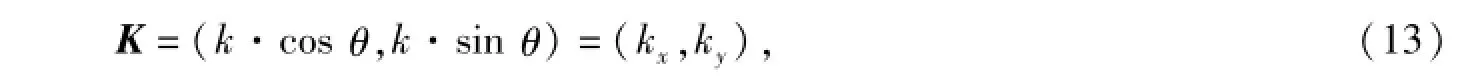
其中k也是相对于海浪波长λ的波数,即k=2π/λ。
1.2 三维海面的FDTD电磁计算
麦克斯韦方程组解释了电与磁相互激励而引起电磁波传播的原理,可以表示为积分方程和微分方程两种形式,FDTD方法是对有限空间离散化后建立差分方程模型。
在FDTD方法中主要利用麦克斯韦方程组的前两个方程,即

其中,E、D、H、B分别为电场强度(V/m)、电通量密度(C/m)、磁场强度(A/m)、磁通量密度(Wb/m2),J和Jm分别为电流密度(A/m2)和磁流密度(V/m2),它们均是时间和空间的函数。各向同性线性介质中的本构关系为

式中ε和μ分别表示介质的介电常数(F/m)和磁导常数(磁导率)(H/m),σ和σm分别表示电导率(S/m)和磁导率(Ω/m)。
图3给出了电磁空间的Yee网格模型[14],对整个仿真空间进行离散化处理并采用中心差分近似计算麦克斯韦旋度方程。
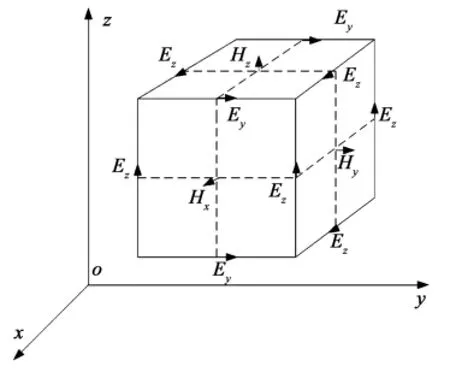
图3 FDTD离散中的Yee元胞Fig.3 Yee cell of a FDTDmodel
在Yee网格模型中,电场与磁场在空间与时间上交替分布,每一个磁场分量由4个电场分量环绕,反之亦然;时间采样上电场和磁场交替存在,采样间隔与起始相位差半个时间步,这种电磁场模型既与电磁感应定律相一致,又便于麦克斯韦方程的差分计算,能够准确地反映电磁场的传播特性。以此模型对麦克斯韦旋度方程进行离散化和差分化处理,将电磁场传播空间划分成周期延拓的Yee元胞,用Δx、Δy、Δz分别表示空间划分的方向间隔,用Δt表示时间采样间隔[15]。对于Ex分量,其差分形式为
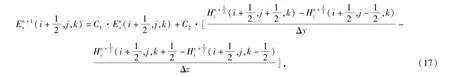
其中
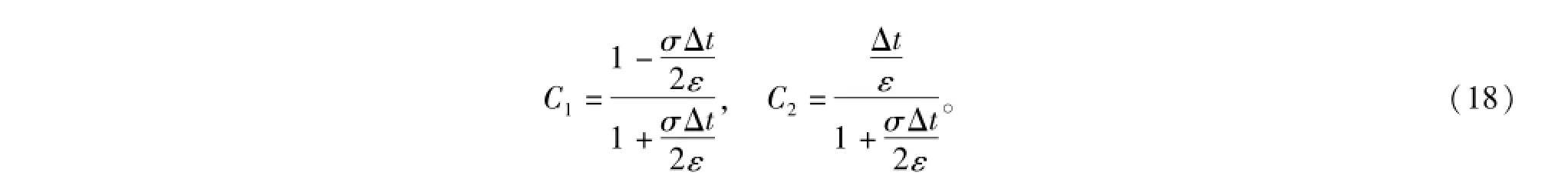
而对Hx分量,其差分形式为
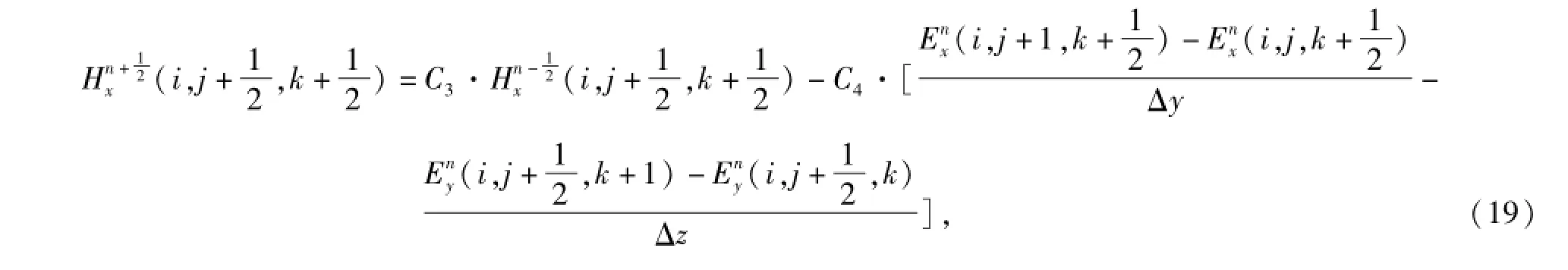
其中
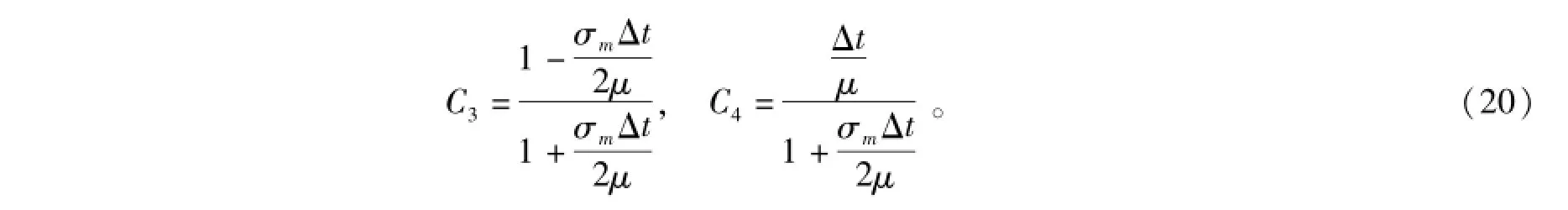
在实际中,物体的电磁散射空间是无限大的,而FDTD方法只能计算有限区域[16],为了对无限区域准确建模,对FDTD的计算区域进行如图4所示的空间和边界划分[17]。
其中,空间划分为总场区与散射区,总场区包括散射目标,散射场区只有散射和反射波,二者之间的边界称为连接边界,散射区最外边称为吸收边界,作为有限模拟区域的边界。同时,由于散射存在近场与远场的区别,在散射区设置输出边界,位于连接边界与吸收边界之间,用于远场近场转变,实现近场数据到远场的外推,模拟电磁传播的特性。电磁波的加载在连接边界上进行,并将入射波限制在总场区内。而在吸收边界上设置恰当的吸收边界条件,以此作为电磁散射空间计算的终结,降低反射波的非物理性反射。总之,连接边界、吸收边界和输出边界的处理是FDTD算法中的三大核心问题[18]。

图4 散射问题中FDTD区域的划分Fig.4 FDTD field division for a scatteringmodel
2 仿真结果与分析
假设雷达距离海平面高度为h,以纵坐标Z表示高度值,令雷达的高度坐标z=0,则海面的高度坐标z=-h,如图5所示,擦地角为β,下视角为α。
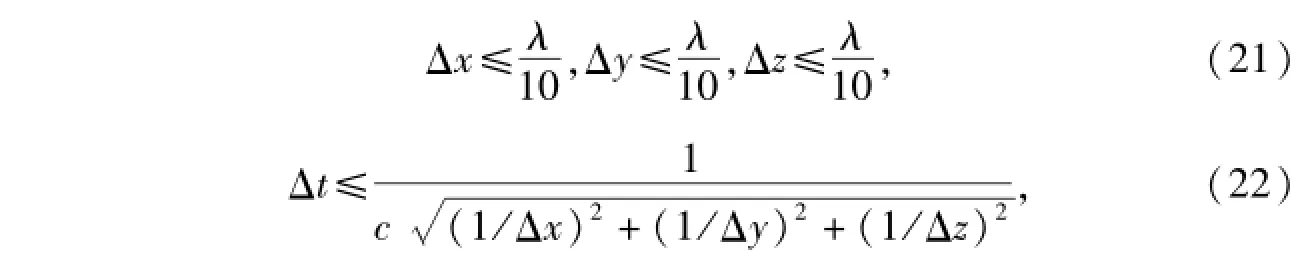

图5 雷达覆盖海面示意图Fig.5 Illustration of radar signal covered ocean surface
这里取离散空间步长为0.3 mm,离散时间步长为5.77×10-12s。因而在不考虑海浪高度的情况下,即在z轴高度方向上只放置1个元胞,则所需要的元胞数目为
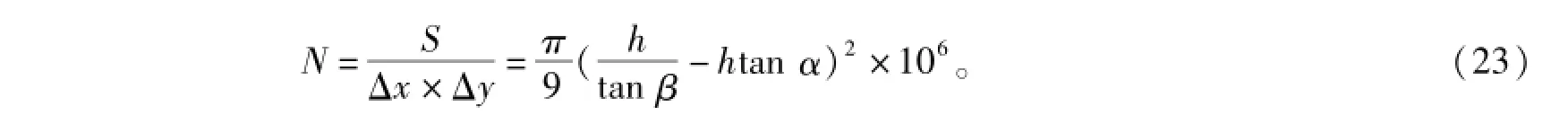
假设风速为8 m/s,平衡海表面上最大海浪的波长约为41 m,假设计算海面的大小为20 m×20 m,浪高为5 m,因而所需计算海面的大小为67 000Δx×67 000Δy×17 000Δz。
图6给出了三维海面目标的仿真结果,其中横坐标分别为100 m×100 m,纵坐标表示海浪高度值,图中结果与真实海面相同,证明了海浪谱模型的有效性。对其电磁参数设置如下:空气的相对介电常数与磁导系数均为1,相对电导率与磁导率为1;海面的相对介电常数与磁导系数也为1,相对电导率为3.27×107S/m,相对磁导率为0Ω/m。信号入射方位角为0.2π(与z轴正方向夹角),俯仰角为0.3π(与x轴正方向夹角)。

图6 粗糙海面的仿真结果Fig.6 Simulation results of rough sea

图7 电场分量Fig.7 Electric field component
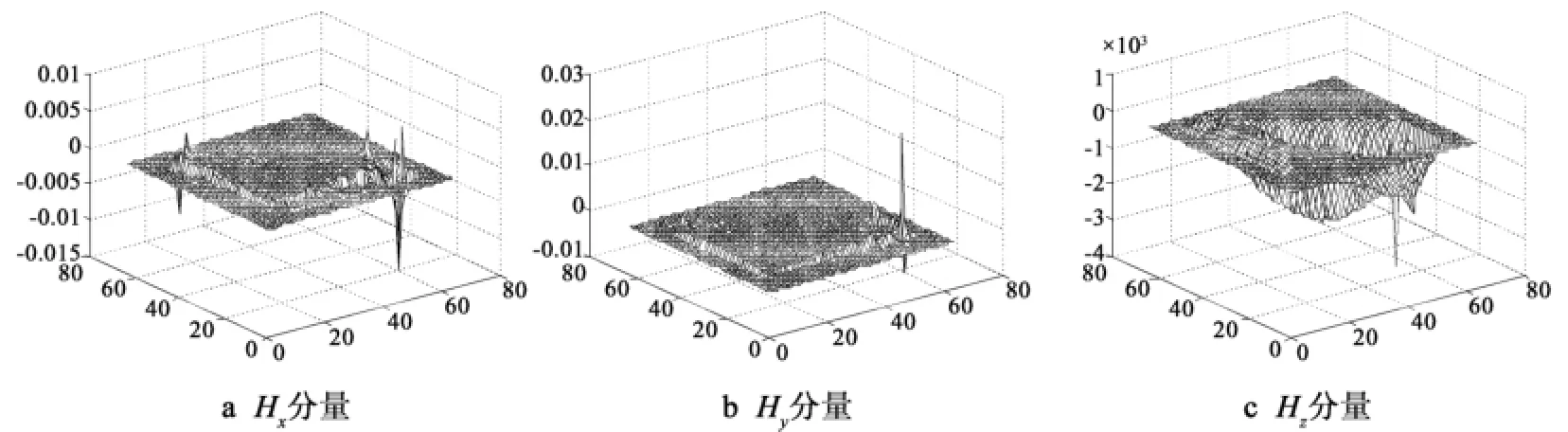
图8 磁场分量Fig.8 Magnetic field component
图7与图8分别给出了总场区内某个平面上的电场与磁场在x,y,z三个方向上的分量的仿真结果,其中横坐标与海面的坐标相对应,纵坐标表示电磁场分量的能量,正负号对应不同的方向,模为能量值。从图中可以看出,在一个一定的方向分量上,电场与磁场此消彼长,如图7的a、b、c分别对应图8的a、b、c,与电磁理论相一致;而电场与磁场本身在不同分量上的分布也与目标的实际情况相符,因此电磁场的分布正确反映了海面的电磁特性。
3 结论
本文针对复杂海面电磁环境难以准确模拟的问题,给出了动态海面及目标电磁仿真的方法。结果表明,该方法能够有效实现完整的海洋电磁散射仿真系统,准确反映海洋表面的电磁散射特性,给出不同分量的值,便于分析散射对回波信号的影响。但雷达信号覆盖海洋面积广阔,FDTD空间迭代步长较小,因此计算量巨大,需要研究高速并行计算方法来实现实时的动态仿真。下一步将以此文工作为基础,在GPU系统上实现目标的加载以及FDTD的实时计算与显示,并将典型海面目标特性加载到模型中。
[1]SKOLNIK M I.雷达手册[M].北京:电子工业出版社,2010:542-545.
[2]唐劲飞,龚沈光,王金根.基于Neumann谱和PM谱的海浪感应磁场能量分布计算[J].海军工程大学学报,2001,13(4):82-86.
[3]陈丽宁,金一丞,任鸿翔,等.海浪绘制中波浪谱的选择和参数计算[J].计算机科学,2013,40(7):283-288.
[4]王珂,张元,洪峻,等.海浪谱的选择对海面电磁波散射建模的影响[J].电讯技术,2013(4):435-439.
[5]赫亮.波浪谱密度函数数值分析[D].大连:大连理工大学,2005.
[6]李维,金亚秋.三维粗糙面上的MIMO信道模型[J].微波学报,2011,27(3):56-60.
[7]郭立新,王运华,吴振森.双尺度动态分形粗糙海面的电磁散射及多普勒谱研究[J].物理学报,2005,54(1):96-101.
[8]JOHNSON JT,ZHANGM.Theoretical study of the small slope approximation for ocean polarimetric thermal emission[J].IEEE Transactions on Geoscience and Remote Sensing,1999,37(5):2305-2316.
[9]FUTAMATA M,MARUYAMA Y,ISHIKAWA M.Local electric field and scattering cross section of Ag nanoparticles under surface plasmon resonance by finite difference time domainmethod[J].The Journal of Physical Chemistry B,2003,107(31):7607-7617.
[10]DING Y,CHEN C S,BEARDSLEY R C,et al.Observational andmodel studies of the circulation in the Gulf of Tonkin,South China Sea[J/OL].Journal of Geophysical Research:Oceans,2013.http://onlinelibrary.wiley.com/doi/10.1002/2013JC009455/full.
[11]陈瑜,胡云安,林涛,等.基于改进分形海浪谱的海浪模拟[J].海军工程大学学报,2012,24(6):21-25.
[12]朱偬.动态海洋环境仿真中的若干关键技术研究[D].武汉:华中科技大学,2010.
[13]侯学隆,黄启来,沈培志.基于FFT的海浪实时仿真方法[J].计算机工程,2009,35(22):256-258.
[14]YEE K S,CHEN JS.The finite-difference time-domain(FDTD)and the finite-volume time-domain(FVTD)methods in solving Maxwell's equations[J].IEEE Transactions on Antennas and Propagation,1997,45(3):354-363.
[15]OSKOOIA F,ROUNDY D,IBANESCU M,et al.MEEP:A flexible free-software package for electromagnetic simulationsby the FDTDmethod[J].Computer Physics Communications,2010,181(3):687-702.
[16]SIMPSON JJ.Global FDTD Maxwell's equations modeling of electromagnetic propagation from currents in the lithosphere[J].IEEE Transactions on Antennas and Propagation,2008,56(1):199-203.
[17]SULLIVAN D M.Electromagnetic simulation using the FDTDmethod[M].Hoboken,NJ:Wiley-IEEE Press,2013.
[18]SYPEK P,DZIEKONSKI A,MROZOWSKIM.How to render FDTD computations more effective using a graphics accelerator[J].IEEE Transactions on Magnetics,2009,45(3):1324-1327.
Physicalmodel based electrom agnetic simulation methodology for dynam ic ocean surface
ZHOU Bin1,LIU En-xiao1,YANG Lei1,LIANG Zh i-heng2,TAO Qing-chang2
(1.Institute of Oceanographic Instrumentation,Shandong Academy of Sciences,Qingdao 266001,China;2.Department of Precision Instrument,Tsinghua University,Beijing 100086,China)
This paper present an electromagnetic simulation method for sea clutter and targets in view of the difficult accurate modeling of complicated sea surface electromagnetic scenario in microwave ocean remote sensing.We employ a ocean wave spectrum model to reconstruct 3D coarse sea surface,consistent with the actual situation.We can therefore set up the corresponding electromagnetic parameters and recover the real sea environment.We further discretize space and time with FDTD and perform iterative computation.We then calculate the dynamic and realtime electromagnetic distribution.We eventually prove the sea surface model by simulation and present the corresponding electromagnetic distribution status.Simulation experiments show that the method can effectively implement the simulation of a complete eletromagnetic scattering from ocean surface.
microwave ocean remote sensing;sea clutter;electromagnetic scattering;FDTD
P715.7;O441.4
A
1002-4026(2014)01-0009-07
10.3976/j.issn.1002-4026.2014.01.002
2013-11-27
装备预研基金重点项目(9140A04020113JW01011)
周斌(1980-),男,博士,副研究员,研究方向为海洋遥感,GPU并行计算。Email:synosy@gmail.com
