车桥耦合系统的近似解研究

郭秀英， 吴启亮， 李海涛

（石家庄铁道大学数理系，河北石家庄 050043）

车桥耦合系统的近似解研究

郭秀英， 吴启亮， 李海涛

（石家庄铁道大学数理系，河北石家庄 050043）

采用GSB方法研究车桥耦合模型一些特殊情况下的近似解。针对车桥耦合模型，由Lagrange方程得到了变刚度SD振子的动力学方程。利用GSB方法对μ（t）作为常数激励的情况进行讨论，得到了非对称系统的含有完全椭圆积分的二阶近似解表达式。利用Matlab进行数值模拟，并将近似结果与原系统进行比较，发现近似解与原系统十分接近。

非线性振动；SD振子；GSB方法；车桥耦合系统；椭圆积分

0 引言

非线性振动理论的研究目的是基于非线性振动系统的数学模型在不同参数和初始条件下，分析系统的近似解及其动力学行为。同时为一系列重大工程中非线性动力学问题的解决提供可操作的理论计算方法，是当今国内外学术发展的重大前沿课题［1-13］。

研究非线性系统动力学的方法可以分为定性（几何方法）和定量方法两大类［14-15］。定性方法一般不直接求解非线性动力系统，而是从非线性系统的动力学方程入手，研究系统在状态空间的动力学行为［14］。由于非线性微分方程一般没有统一的精确解法，所以定量方法只研究各种近似解，常用的方法如平均法，多尺度法，谐波平衡法等等［15］。定性方法和定量方法可以相互补充，定性方法可以得到系统解的拓扑结构和系统参数之间的关系，定量方法可以得到参数确定时系统的数值解，在研究各种复杂的非线性动力学问题时，两种方法缺一不可。随着计算机代数、数值模拟和图形技术的进步，非线性动力学理论正在从低维向高维发展，非线性动力学理论和方法所能处理的问题的规模和难度不断提高，已逐步接近实际系统［1-13］。

悬索桥也叫吊桥，指由受拉悬索作为承重结构的桥梁［16］。其中不设加劲梁，或加劲梁高度很小的悬索桥，称为柔性吊桥。柔性吊桥，因其桥面系构造简单、加工容易、耗钢量低、桥梁架设和维护方便、桥型美观、造价低，在农村和旅游景点有广泛的应用前景。目前，柔性吊桥的理论研究主要集中在建立数学模型，利用VBA作为AutoCAD的二次开发工具，开发柔性吊桥桥型成图系统上［16］，利用Visual Basic 6.0开发悬索设计系统［17］。

关于移动车辆载荷下桥梁振动的研究，不管古典理论还是现代理论，研究热点集中在求振动微分方程的精确解和响应方程，以期找到该强迫振动的共振条件。由于车桥耦合系统的动力特性随载荷位置的移动而不断变化，共振条件只能在短时间内满足，再加上该问题的振动微分方程带有变系数以及车辆载荷在桥上通过的时间也是有限的，使得该问题的研究比较复杂。因此，建立一个合适的数学模型，比较简单方便地研究移动载荷作用下桥的跨中挠度一直是理论工作者探讨的热点问题。文献［18］利用变刚度SD振子模拟移动载荷和柔性吊桥的耦合系统，探讨了若干移动载荷相继过桥时，柔性吊桥跨中挠度的非线性动力学行为。本文通过GSB（Generalized Senator-Bapat）方法［19］得到了该系统的近似解。最后通过数值仿真验证了理论分析的正确性。

1 车桥耦合模型初步分析

移动载荷和柔性吊桥的耦合系统的运动微分方程为［18］

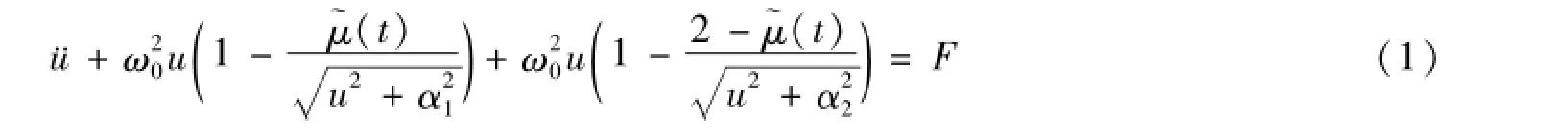
式中，u和t分别为无量纲化的位移和时间；ω0为固有频率；μ（t），α1，α2为参数激励；F为常数激励；

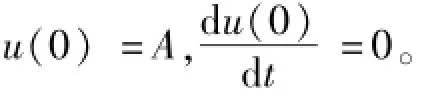
在忽略重力作用的情况下有

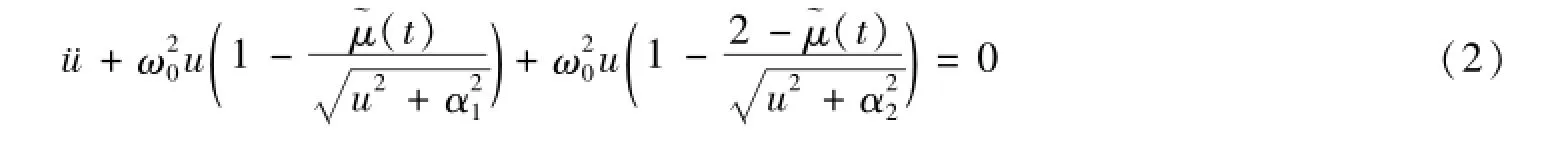
令τ＝ωt，则方程（2）变为

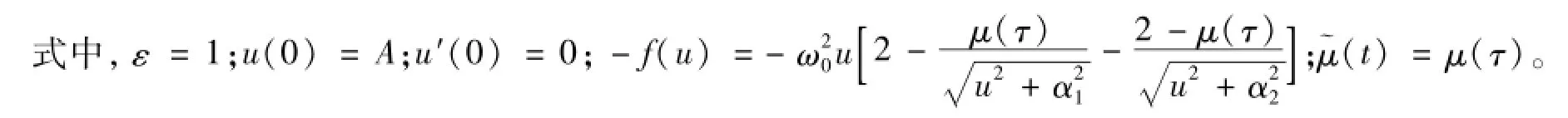
式（3）中植入的参数φ是由常见的LP摄动技术决定的，因此，式（3）的近似解可展开成如下形式

2 车桥耦合模型的近似解

3 数值模拟

为了进一步验证采用GSB方法求得的二阶近似解与原系统精确解的近似程度，通过Matlab做出了该系统二阶近似解和精确解的图形。首先对系统满足GSB方法的周期求解。

特别的，取μ（τ）＝λ，式（3）可表示为

图1和图2分别是当α1＝3α2和α1＝6α2时，系统的二阶近似解和精确解的对比图。从两图中不难看出由GSB方法求得的二阶近似解与原系统精确解的近似程度比较理想。

图1 α1＝3α2，A＝1时系统的近似解与精确解对比

图2 α1＝6α2，A＝1时系统的近似解与精确解对比

4 结论与模型展望

采用GSB方法分析了变刚度耦合SD振子的二阶近似解。在求解系统的二阶近似解的过程中，讨论了μ（t）作为常数激励的情况下，系统的二阶近似解的情况。

对GSB方法讨论，本文只计算了激励参数为常数的二阶近似解，还可经过改进GSB方法得到更精确的近似解。在今后的研究中可以通过对变化的时间状态进行考虑，该情况更能反映一般事实。

［1］PAVLOVSKAIA EE，WIERCIGROCH M，WOO K C，etal.Modelling of groundmoling dynamics by an impact oscillator with a frictional slider［J］.Meccanica，2003（38）：85-97.

［2］PAVLOVSKAIA E，KARPENKO E V，WIERCIGROC H M.Nonlinear dynamic interactions of a Jeffcott rotorwith a preloaded snubber ring［J］.Sound Vib.，2004，276：361-379.

［3］BANERJEE S，CHAKRABARTY K.Nonlinearmodeling and bifurcations in the boost converter［J］.IEEE Trans.on Power E-lectronics，1998，13（2）：252-260.

［4］BANERJEE S，OTT E，YORKE JA，et al.Anomalous bifurcations in DC-DC converters：boder line collisions in piecewise smoothmaps［C］／／Power Electronics Specialists Conference.The 28th Annual IEEE，1997（2）：1337-1344.

［5］张琪昌，田瑞兰，王炜.一类机电耦合非线性动力系统的混沌动力学特征［J］.物理学报，2008，57（5）：2799-2804.

［6］曹庆杰，田瑞兰，韩彦伟.SD振子的非线性动力学特征研究［J］.石家庄铁道学院学报：自然科学版，2010，23（2）：32-37.

［7］陆启韶.常微分方程的定性方法和分岔［M］.北京：北京航空航天大学出版社，1989.

［8］Tian R L，CaoQ J，Yang SP.The codimention-two bifurcation for the recent proposed SD oscillator［J］.Nonlin.Dyn.，2010，59：19.

［9］Tian R L，Cao Q J，Li Z X.Hopf bifurcations for the represently proposed smooth-and-discontinuous oscillator［J］.Chin. Phys.Lett.，2010，27（7）：074701.

［10］Tian R L，Yang XW，Cao Q J，etal.Chaotic threshold for nonlinear dynamical systemswith an irrational restoring force［J］.Chin.Phys.，2012，B 21：020503.

［11］Tian R L，Wu Q L，Liu Z J，etal.Dynamic analysis of the smooth-and-discontinuous oscillator under constant excitation［J］. Chinese Physical Letters，2012，29（8）：084706.

［12］郭数起，杨绍普.一类非等截面杆的纵向自由振动［J］.石家庄铁道学院学报：自然科学版，2010，23（2）：59-63.

［13］郜浩冬，陈恩利，李黎阳.参激单摆非线性系统动力学的实验研究［J］.石家庄铁道大学学报：自然科学版，2010，24（3）：34-39.

［14］杨绍普，申永军.滞后非线性系统的分岔与奇异性［M］.北京：科学出版社，2003.

［15］陈树辉.强非线性振动系统的定量分析方法［M］.北京：科学出版社，2007.

［16］官印生，周新年，郏丽凤，等.基于VB的柔性吊桥悬索设计系统［J］.东北林业大学学报，2006，34（3）：1-5.

［17］王贵春，潘家英，张欣.大跨度铁路斜拉桥车桥耦合振动非线性分析［J］.应用力学学报，2008，25（3）：524-528.

［18］Tian R L，Yang XW.Nonlinear vibration characteristics of flexible suspension bridge undermoving load［J］.Applied Material Research，2011，179／180：1025-1030.

［19］Lai SK，Xiang Y.Application of ageneralized Senator Bapatperturbation technique tononlinear dynamical systemswith an irrational restoring force［J］.Computers and Mathematics with Applications，2010，60：2078-2086.

Research of Approximate Solutions for Vehicle-bridge Coup led Vibration System

Guo Xiuying， Wu Qiliang， Li Haitao

（Dept ofMath＆Phys，Shijiazhuang Tiedao University，Shijiazhuang 050043，China）

In order to research the approximate solutions for vehicle-bridge coupled vibration，we established a vehicle-bridge coupled model，and obtained the dynamic equations of the variable stiffness SD oscillator with the Lagrange equation.We discussed the situations that the parameter is a constant excitation by GSB perturbation technique respectively.Finally，we obtained the expression of the second-order approximate solution of the asymmetric system which contains the complete elliptic integral.The approximate solution has been compared with the exact solution of original system with the help of MATLAB numerical stimulation tools，and it is found that the result is approximate to the original system.

nonlinear oscillation；SD oscillator；GSB perturbation technique；vehicle-bridge coupled vibration system；elliptic integral

O322

A文章编号：2095 0373（2014）01 0001 08

（责任编辑 车轩玉）

10.13319／j.cnki.sjztddxxbzrb.2014.01.01

2013 03 28

郭秀英 女 1976年出生 讲师

国家自然科学基金（11002093）；石家庄铁道大学科研启动金（Q21）