Lower Bounds on the(Laplacian)Spectral Radius of Weighted Graphs∗

Aimei YU Mei LU

1 Introduction

In this paper,we consider a simple connected weighted graph in which the edge weights are positive numbers.LetG=(V,E)be a simple connected weighted graph with a vertex setV={v1,v2,···,vn}.We denote bythe weight of the edgeand assume=For short,we writei∼jif the verticesviandvjare adjacent.Forvi∈V,let=w(vi)=wij.IfGis a weighted graph with=wjfor any∈V,thenGis called a regular weighted graph.IfG=(X∪Y,E)is a weighted bipartite graph withwi=wjfor anyvi,vj∈Xandfor any,∈Y,thenGis called a semiregular weighted bipartite graph.

Forvi∈V,letγi=γ(vi)=IfGis a weighted graph withfor any∈V,thenGis called a pseudo-regular weighted graph.IfG=(X∪Y,E)is a weighted bipartite graph withfor anyvi,vj∈Xandfor anyvk,vl∈Y,thenGis called a pseudo-semiregular weighted bipartite graph.Obviously,any regular weighted graph is a pseudo-regular weighted graph and any semiregular weighted bipartite graph is a pseudo-semiregular weighted bipartite graph.

The adjacency matrixA(G)of a weighted graphGis defined asA(G)=where

LetW(G)=diag(w1,w2,···,wn).Then the Laplacian matrixL(G)of a weighted graphGisL(G)=W(G)−A(G).The signless Laplacian matrixQ(G)of a weighted graphGisQ(G)=W(G)+A(G).Clearly,A(G),L(G)andQ(G)are real symmetric matrices.Hence their eigenvalues are real numbers.We denote by(M)the largest eigenvalue of a real symmetric matrixM.For a weighted graphG,we denote by(G),(G)and(G)the largest eigenvalues ofA(G),L(G)andQ(G),respectively,and call them the spectral radius,the Laplacian spectral radius and the signless Laplacian spectral radius ofG,respectively.WhenGis connected,A(G)andQ(G)are irreducible matices and so by Perron-Frobenius Theorem,(G)and(G)are simple with the positive eigenvectors.

If=1 for all edgesthenGis an unweighted graph.For an unweighted graph,wi=w()=is the degree of∈V(G),andis the 2-degree ofThere exists a vast literature that studies the bounds of the spectral radius,the Laplacian spectral radius and the signless spectral radius.We refer the reader to[1,7–8,10–13,15–16,21]for more information.

For weighted graphs,Yang,Hu and Hong[19]gave the upper and lower bounds of the spectral radius of the weighted trees;Das and Bapat[6]and Sorgun and Bykkse[17]gave some upper bounds of the spectral radius;Rojo[14]and Das[4–5]gave some upper bounds of the Laplacian spectral radius.

The remainder of this paper is organized as follows.In Section 2,we give some useful lemmas.In Section 3,we present some lower bounds of the spectral radius of weighted graphs.In Section 4,we give some lower bounds of the signless Laplacian spectral radius of weighted graphs,from which we can get some lower bounds of the Laplacian spectral radius of weighted graphs.From these bounds,we can deduce some known lower bounds on the spectral radius and the Laplacian spectral radius of unweighted graphs.

2 Some Lemmas

The following are some useful lemmas.

Lemma 2.1(see[10])Let A be a nonnegative symmetric matrix and x be a unit vector of.If(A)=Ax,then Ax=(A)x.

Lemma 2.2(see[18])Let G be a simple connected weighted bipartite graph.Then(G)=(G).

ProofLetG=(X∪Y,E)be a connected weighted bipartite graph withnvertices and suppose thatX=Y=LetU=()be then×ndiagonal matrix with=1 if 1≤i≤kand=−1 ifk+1≤i≤n.It is easy to see thatL(G)U=Q(G),which implies thatL(G)andQ(G)have the same spectrum.Henceμ1(G)=q1(G).

Lemma 2.3(see[2])Let M=()be an n×n irreducible nonnegative matrix with the spectral radius ρ(M),and(M)be the i-th row sum of M for1≤i≤n.Then

Moreover,either equality holds if and only if the row sums of M are all equal.

By Lemma 2.3,the following result holds immediately.

Lemma 2.4Let G be a simple connected weighted graph.Then

Moreover,either equality holds if and only if G is a regular weighted graph.

Lemma 2.5(see[5])Let G be a simple connected weighted graph.Then

where the equality holds if and only if G is a regular weighted bipartite graph or a semiregular weighted bipartite graph.

3 Lower Bounds of the Spectral Radius

The following theorem is one of our main results.

Theorem 3.1Let G be a simple connected weighted graph of order n.Then

where the equality holds if and only if G is a pseudo-regular weighted graph or a pseudosemiregular weighted bipartite graph.

ProofLetA(G)be the adjacency matrix ofGandX=be the unit positive eigenvector ofA(G)corresponding toλ1(A(G)).For short,we writeA(G)asAin the following proof.Take

Noting thatCis a unit positive vector,we have

Since

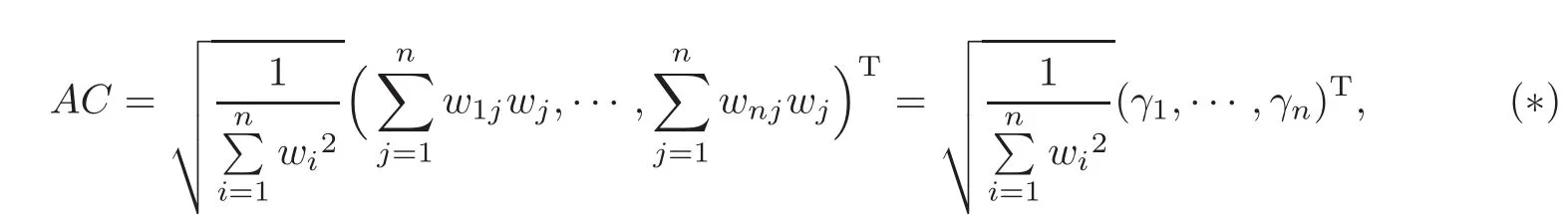
we have

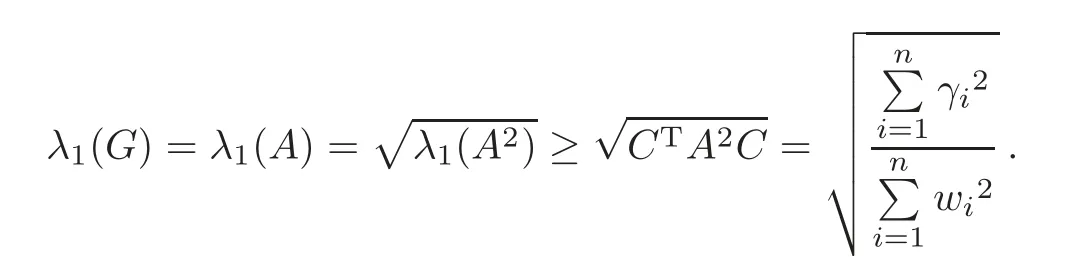
If the equality holds,then

By Lemma 2.1,C=C.If the multiplicity ofis one,thenX=C,which implies=(G)(1≤i≤n).HenceGis a pseudo-regular weighted graph.Otherwise,the multiplicity of(A2)=((A))2is two,which implies that−λ1(A)is also an eigenvalue ofG.ThenGis a connected bipartite graph by a theorem of Frobenius(see,for example,[3,Theorem 0.3]).Without loss of generality,we assume

whereB=is ann1×n2matrix withn1+n2=n.Let

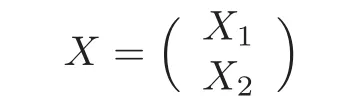
and

whereX1=X2=andC2=Since

we have

and

Noting thatBBTandBTBhave the same nonzero eigenvalues,λ1(A2)is the spectral radius ofBBTand its multiplicity is one.Sois a constant),which implies(1≤i＜j≤n1).Similarly,is a constant),which implies(n1+1≤i＜j≤n).HenceGis a pseudo-semiregular weighted graph.

Conversely,ifGis a pseudo-regular weighted graph,then=p(1≤i≤n)is a constant,which impliesAC=pC.By Perron-Frobenius Theorem(see[2]),for any positive eigenvector of a nonnegative matrix,the corresponding eigenvalue is the spectral radius of that matrix.

Henceλ1(G)=p=

IfGis a pseudo-semiregular weighted bipartite graph,we assume

(1≤i≤n1)and(n1+1≤i≤n),whereB=)is ann1×n2matrix withn1+n2=n.LetC1=andC2=So for eachi(1≤i≤n1),thei-th element ofBBTC1is

Similarly,rj(BTBC2)=for eachj(1≤j≤n2).HenceA2C=p1p2C,whereC=(w1,w2,···,wn)T.It is known that for any positive eigenvector of a nonnegative matrix,the corresponding eigenvalue is the spectral radius of that matrix.So

From the equality(∗),we have

It follows that

This completes the proof of Theorem 3.1.

Corollary 3.1(1)Let G be a pseudo-regular weighted graph with γ(v)=pw(v)for each v∈V(G).Then(G)=p.

(2)Let G be a pseudo-semiregular weighted bipartite graph with the bipartition(X,Y).If γ(v)=pxw(v)for each v∈X and γ(v)=pyw(v)for each v∈Y,then λ1(G)=

Since a regular weighted graph must be a pseudo-regular weighted graph and a semiregular weighted bipartite graph must be a pseudo-semiregular weighted bipartite graph,we have the following results immediately from Corollary 3.1.

Corollary 3.2(1)Let G be a regular weighted graph with w(v)=a for each v∈V(G).Then λ1(G)=a.

(2)Let G be a semiregular weighted bipartite graph with the bipartition(X,Y).If w(v)=a for each v∈X and w(v)=b for each v∈Y,then λ1(G)=

Corollary 3.3Let G be a simple connected weighted graph of order n.Then

where the equality holds if and only if G is a regular weighted graph or a semiregular weighted bipartite graph.

ProofBy Theorem 3.1 and the Cauchy-Schwarz inequality,

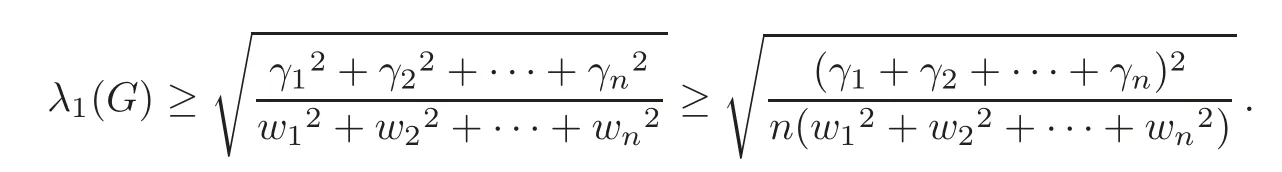
Since

we have

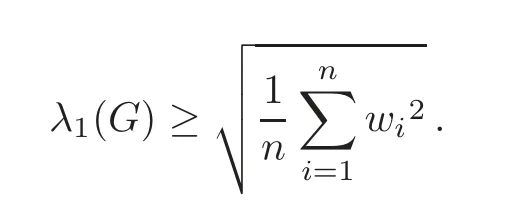
If the equality holds,Gis a pseudo-regular weighted graph or a pseudo-semiregular weighted bipartite graph(by Theorem 3.1)withγi=γjfor all 1≤i＜j≤n.ThusGis a regular weighted graph or a semiregular weighted bipartite graph.Conversely,ifGis a regular weighted graph,the equality holds immediately.IfGis a semiregular weighted bipartite graph,weassume thatw(v1)=···=w(vn1)=aand=···=w()=b.Sincea=(n−)b,By Corollary 3.2,we have(G)=Thus the equality holds.

Corollary 3.4Let G be a simple connected weighted graph of order n.Then

ProofBy Corollary 3.3 and the Cauchy-Schwarz inequality,

Remark 3.1IfGis a simple connected unweighted graph of ordernwith the degree sequenced1,d2,···,dn,the minimum degreeδ,andti=then the inequalities(3.1),(3.2)and(3.3)become

respectively.The inequality(3.4)is one of the main results in[20],and the inequality(3.5)is one of the main results in[9].

4 Lower Bounds of the(Signless)Laplacian Spectral Radius

Theorem 4.1Let G be a simple connected weighted graph of order n.Then

where the equality holds if and only if G is a regular weighted graph or a semiregular weighted bipartite graph.

ProofLetW(G)+A(G)be the signless Laplacian matrix ofGandX=be the unit positive eigenvector ofW(G)+A(G)corresponding toq1(G).For short,we writeW(G)+A(G)asW+Ain the following proof.Take

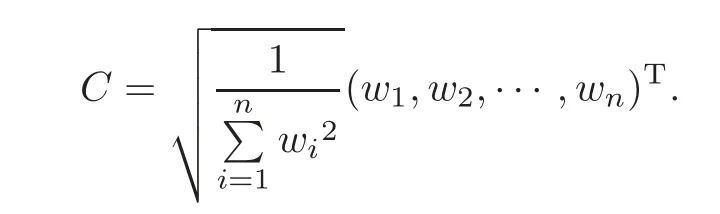
Then

Since

we have

If the equality holds,then

which implies that(W+A)2C=((W+A)2)C(by Lemma 2.1).SinceW+Ais a nonnegative irreducible positive semidefinite matrix,all eigenvalues ofW+Aare nonnegative.By Perron-Frobenius Theorem,the multiplicity of(W+A)is one.Since((W+A)2)=((W+A))2,we have the multiplicity ofλ1((W+A)2)is one.Hence,if the equality holds,thenX=C.Byλ1(W+A)C=(W+A)C,we haveλ1(W+A)wi=+γifori=1,2,···,n.Thus+=+for alli/j.Assume,without loss of generality,thatw1=a=max{wi:1≤i≤n},w2=b=min{wi:1≤i≤n}andab.Then we have

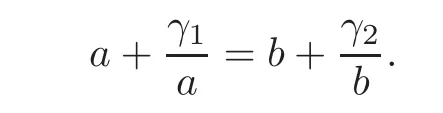
Sinceγ1≥abandγ2≤ab,

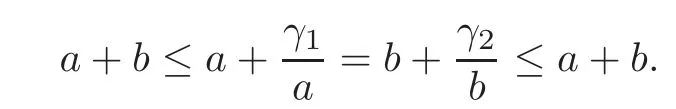
Thus we must haveγ1=ab=γ2.This impliesw(v)=aorw(v)=bfor allv∈V(G),sinceGis a connected weighted graph.HenceGis a regular weighted graph or a semiregular weighted bipartite graph.

Conversely,ifGis a regular weighted graph withw(v)=afor eachv∈V,then

By Lemma 2.4,q1(G)=2aand so the equality holds.

IfGis a semiregular connected bipartite graph withw(v1)=···=w(vn1)=aand=···=w(vn)=b,noting thatn1a=(n−n1)b,we have

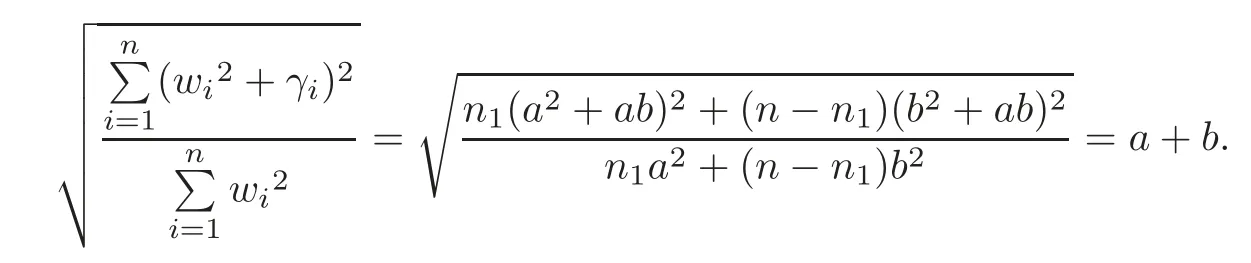
By Lemmas 2.2 and 2.5,q1(G)=μ1(G)=a+band so the equality holds.

Corollary 4.1Let G be a simple connected weighted graph of order n.Then

where the equality holds if and only if G is a regular weighted graph.

ProofBy Theorem 4.1 and the Cauchy-Schwarz inequality,we have

If the equality holds,Gis a regular weighted graph or a semiregular bipartite weighted graph(by Theorem 4.1)withfor 1≤i＜j≤n.IfGis a semiregular bipartite weighted graph,without loss of generality,we assume thatw1=a=max{wi:1≤i≤n}andw2=b=min{wi:1≤i≤n}.Then we have+ab,which impliesa=b.HenceGis a regular bipartite weighted graph.Conversely,ifGis a regular weighted graph,by Lemma 2.4,the equality holds immediately.

Corollary 4.2Let G be a simple connected weighted graph.Then

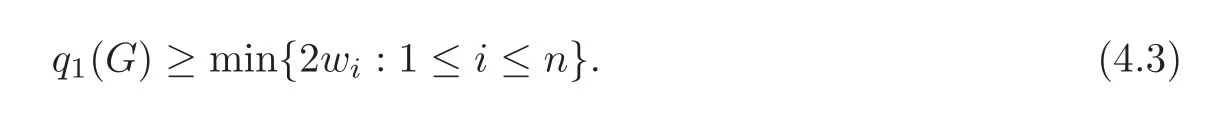
ProofBy Corollary 4.1 and the Cauchy-Schwarz inequality,

Remark 4.1LetGbe a simple connected unweighted graph with the degree sequenced1,d2,···,dn,the minimum degreeδ,andti=Then the inequalities(4.1),(4.2)and(4.3)become

respectively.

By Lemma 2.2,for a simple connected weighted bipartite graphG,its Laplacian spectral radiusμ1(G)is equal to its signless Laplacian spectral radiusq1(G).So by Theorem 4.1 and Corollaries 4.1–4.2,the following results hold immediately.

Theorem 4.2Let G be a simple connected bipartite weighted graph of order n.Then

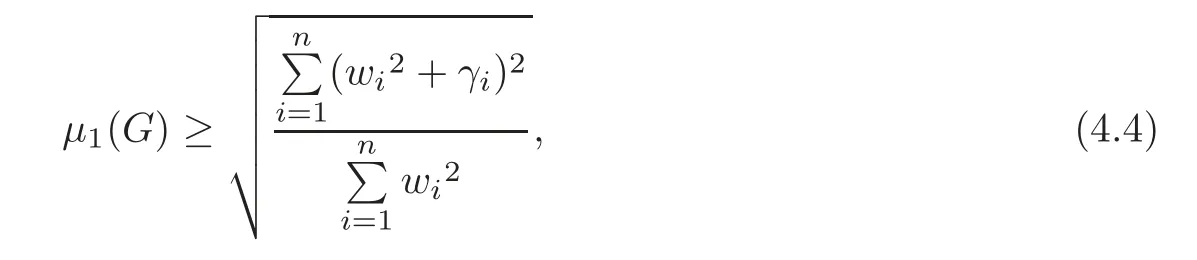
where the equality holds if and only if G is a regular weighted bipartite graph or a semiregular weighted bipartite graph.

Corollary 4.3Let G be a simple connected bipartite weighted graph of order n.Then

where the equality holds if and only if G is a regular weighted bipartite graph.

Corollary 4.4Let G be a simple connected bipartite weighted graph.Then

Remark 4.2LetGbe a simple connected unweighted graph with the degree sequenced1,d2,···,dn,the minimum degreeδ,andti=Then the inequalities(4.4),(4.5)and(4.6)become

respectively.The inequality(4.7)is one of the main results in[20],and the inequality(4.8)is one of the main results in[10].

[1]Anderson,W.N.and Morley,T.D.,Eigenvalues of the Laplacian of a graph,Linear and Multilinear Algebra,18,1985,141–145.

[2]Bapat,R.B.and Raghavan,T.E.S.,Nonnegative Matrix and Applications,Cambridge University Press,Cambridge,1997.

[3]CvetkoviD.,Doob,M.and Sachs,H.,Spectra of Graphs–Theory and Application,Academic Press,New York,1980.

[4]Das,K.C.,Extremal graph characterization from the upper bound of the Laplacian spectral radius of weighted graphs,Linear Algebra and Its Applications,427,2007,55–69.

[5]Das,K.C.and Bapat,R.B.,A sharp upper bound on the largest Laplacian eigenvalue of weighted graphs,Linear Algebra and Its Applications,409,2005,153–165.

[6]Das,K.C.and Bapat,R.B.,A sharp upper bound on the spectral radius of weighted graphs,Discrete Mathematics,308,2008,3180–3186.

[7]Das,K.C.and Kumar,P.,Some new bounds on the spectral radius of graphs,Discrete Mathematics,281,2004,149–161.

[8]Guo,J.M.,A new upper bounds for the Laplacian spectral radius of graphs,Linear Algebra and Its Applications,400,2005,61–66.

[9]Hofmeister,M.,Spectral radius and degree sequence,Math.Nachr.,139,1988,37–44.

[10]Hong,Y.and Zhang,X.D.,Sharp upper and lower bounds for largest eigenvalue of the Laplacian matrices of trees,Discrete Mathematics,296,2005,187–197.

[11]Li,J.S.and Zhang,X.D.,On the Laplacian eigenvalues of a graph,Linear Algebra and Its Applications,285,1998,305–307.

[12]Liu,H.Q.,Lu,M.and Tian,F.,On the Laplacian spectral radius of a graph,Linear Algebra and Its Applications,376,2004,135–141.

[13]Merris,R.,Laplacian matrices of graphs:A survey,Linear Algebra and Its Applications,197-198,1994,143–176.

[14]Rojo,O.,A nontrivial upper bound on the largest Laplacian eigenvalue of weighted graphs,Linear Algebra and Its Applications,420,2007,625–633.

[15]Rojo,O.,Soto,R.and Rojo,H.,An always nontrivial upper bound for Laplacian graph eigenvalues,Linear Algebra and Its Applications,312,2000,155–159.

[16]Shu,J.L.,Hong,Y.and Kai,W.R.,A sharp bound on the largest eigenvalue of the Laplacian matrix of a graph,Linear Algebra and Its Applications,347,2002,123–129.

[17]Sorgun,S.and Bykkse,S.,The new upper bounds on the spectral radius of weighted graphs,Applied Mathematics and Computation,218,2012,5231–5238.

[18]Tan,S.W.,On the Laplacian spectral radius of weighted trees with a positive weight set,Discrete Mathematics,310,2010,1026–1036.

[19]Yang,H.Z.,Hu,G.Z.and Hong,Y.,Bounds of spectral radii of weighted trees,Tsinghua Science and Technology,8,2003,517–520.

[20]Yu,A.M.,Lu,M.and Tian,F.,On the spectral radius of graphs,Linear Algebra and Its Applications,387,2004,41–49.

[21]Zhang,X.D.,Two sharp upper bound for the Laplacian eigenvalues,Linear Algebra and Its Applications,376,2004,207–213.