连续梁顶板压溃修复过程局部应力分析

简方梁,李 辉,胡国华,李 昊

连续梁顶板压溃修复过程局部应力分析

简方梁,李 辉,胡国华,李 昊

(中铁工程设计咨询集团有限公司,北京 100055)

综合利用ANSYS软件的“单元生死”及多步求解技术,建立精细化实体有限元模型,分析了某连续梁顶板拆除及修复过程中局部应力分布及变化规律。得出:顶板拆除后,剩余顶板纵横向应力普遍增加3 MPa左右,局部角点出现应力集中;顶板修复及加强后,由于二期恒载及活载的作用,老混凝土纵向应力会继续增加,而横向应力基本不会发生变化。在承受二期恒载及活载前后,最大主压应力及最大主拉应力改变不大,但结构局部应力集中点主压应力达到21.7 MPa,应引起注意。

连续梁;生死单元;局部应力

1 概述

连续梁跨越能力较强,且施工方法成熟,在铁路客运专线上得到了广泛应用[1-2]。某连续梁在施工过程中,出现了运架桥机由于操作失误,将顶板局部压溃的问题。顶板压溃位置如图1所示:在连续梁边跨距梁端10.75 m、横向距桥梁中心线左右各0.95 m处,顶板局部压溃形成了2个大小为32 cm×30 cm,深约4 cm的压溃区。顶板底面纵向约5.6 m、横向约4 m范围内混凝土不同程度出现开裂、保护层脱落、顶板底面钢筋外露等现象。顶板纵向预应力束及顶板横向预应力筋及两侧锚头,均无异常。

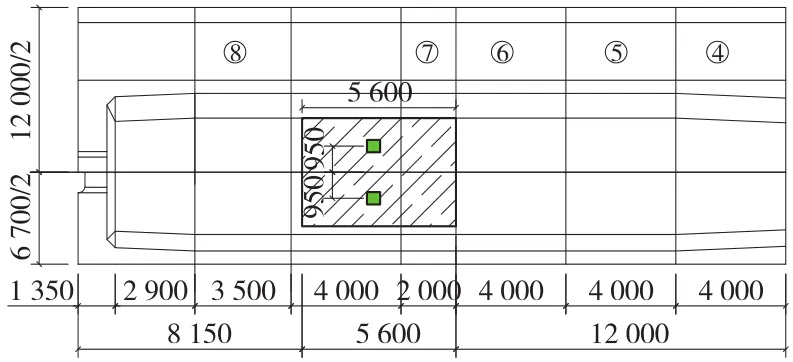
图1 顶板破坏位置(单位:mm)

该事故由于预应力并未失效,更多的是造成结构顶板的局部应力重分布及后续施工运营阶段结构的局部薄弱,而这种应力重分布很难应用整体杆系有限元分析得出理想结果,为更好地指导修复加固,参考相应文献,进行局部分析非常必要[3-7]。本文针对这一问题进行研究,综合利用ANSYS软件的“单元生死”技术及多步求解技术,通过建立精细实体有限元模型,完整地模拟整个事件发生及修复过程,分析各个阶段顶板及开裂薄弱截面应力的变化及应力的量值大小,较好地解决了该问题。

2 有限元模型

2.1 建模思路

(1)结构的变化及应力的转移释放

整个分析过程为:结构顶板局部破坏,破坏结构拆除,退出工作,应力向周边转移;结构修复及补强,新浇结构投入工作,与原有结构共同分担二期恒载及运营阶段的荷载。

综合应用ANSYS软件的“单元生死”技术及多步求解技术实现这一过程。其中,“单元生死”技术在有限元模型建立时建全部需要结构,而在各求解步,通过“杀死”和“激活”结构,完成不同求解步中结构的变换,其实现原理为将“杀死单元”的刚度矩阵乘以一小的系数因子,从而去除其在总刚中的影响,每步求解时仅计及激活单元的荷载及刚度[8-10]。而多步求解则可将上步荷载及结构刚度产生的应力状态作为下步计算的初始条件。通过上述2种技术的结合,可以较好实现整个过程的模拟。

(2)预应力筋的模拟

事件发生在施工架梁阶段,结构承受的最主要荷载为自重及预应力两种,因此预应力模拟的好坏直接影响到结果分析的精度,而局部分析模型涉及的预应力很多且较复杂,包括顶板横向预应力筋、纵向预应力筋、腹板筋、底板筋及竖向精扎螺纹筋等。其中除了竖向筋可直接通过等效荷载施加外,其他均应该采用实体筋的方式,建立杆件力筋模型,精确地模拟预应力效应。

通常实体力筋法在ANSYS软件中有3种处理方式:切分法、节点耦合、约束方程法[9-12]。这3种方法均建立杆单元预应力筋及实体结构模型,切分法将实体结构通过切分,确定预应力筋的位置,预应力筋为实体模型上的某条线,力筋与实体结构自然共节点,力筋计算位置准确,精度高,但是预应力筋几何形状较为复杂时,切分困难,易造成实体模型的不规则,网格划分困难[13];节点耦合法分别建立力筋与结构模型,分别进行有限元网格剖分,然后通过将力筋节点与附近结构点一一对应耦合,实现预应力的施加和共同受力。约束方程法与节点耦合法类似,力筋与结构的联系通过力筋与其周边结构多个节点建立位移约束方程的方式实现。这2种方法的计算精度与网格划分的合理程度有很大关系,相比较而言,约束方程法较容易实现,且对网格的适应力更强。

本次模拟针对具体问题,对顶板纵横向预应力,通过切分法实现,一方面,这部分力筋对结构的分析影响最大,需要准确建模,切分法的准确度最高;另一方面,顶板力筋几何形状相对比较简单,便于切分的操作。对腹板及底板力筋,采用约束方程法,主要原因为该部分预应力筋几何形状复杂,不利于切分法的应用,且该部分的应力筋对结构待分析局部的影响相对较小。采用该种方法可以在较好的精度下简化建模的难度。

2.2 有限元计算模型

根据上述思路,采用ANSYS软件建立有限元模型如图2所示,由于结构及荷载在横桥向基本对称,建立半结构模型。建模范围为边梁0～25.75 m范围,该范围可以适当减小由于局部边界条件对分析区域应力的影响,又不至于使得分析模型过于庞大。其中,混凝土箱梁采用实体单元SOLID45模拟,预应力筋采用杆单元LINK10模拟,局部压溃区域附近网格单元尺寸适当细化,共计实体单元108 478个,杆单元3 045个。

图2 有限元模型

整个模拟分为4个阶段。

阶段1:按照设计结构激活相应单元,施加重力荷载及预应力荷载,施加自整体模型中读出的力的边界条件。打开大变形选项,进行结构静力非线性计算。

阶段2:“杀死”部分开裂顶板及压溃部分,拆除范围为箱梁顶板与部分翼缘板,为了避免应力过于集中,设置了0.5 m×0.85 m导角;为保证拆除部位横向刚度不至于剧烈变化,拆除顶板时,在相应范围腹板内侧设置5道工字钢横撑,间距1.5 m。该阶段模拟拆除部分顶板造成的应力重分布。

阶段3:混凝土桥面板及顶板底部加强段浇筑完成。重新激活阶段2中杀死的单元,并激活顶板底部补强部分结构单元。该阶段为后续二期恒载及活载时的共同受力做准备。

阶段4:有限元模型同阶段3,施加二期恒载及活载于桥面板,模拟新浇结构与原结构共同受力。

各阶段顶板损坏处的细节模型见图2(c)。

边界条件及荷载:

采用从整体模型中读取力的边界条件施加至局部模型:模型右端固定约束,截面左侧的边支反力以外荷载的形式施加于结构上。这样既可保证结构受力与整体模型的一致性,又可简化力边界条件的输入。

荷载除了整体模型中得到的支反力外,在前三阶段仅有自重及预应力。在第4阶段将二期恒载及活载以面力的形式施加于桥面板上。其中二期恒载为均布荷载,活载按整体支反力反算得到,并适当考虑车头的不利因素,在结构裂缝范围内面力较大,其他区域较小。

3 结果分析

3.1 各阶段纵向应力

开裂区左侧截面各阶段纵向应力云图如图3所示。从图中可以看出:

(1)阶段1,在设计截面情况下,截面顶板压应力为1.7～3.5 MPa;阶段2,由于部分顶板拆除,退出工作,剩余顶板应力变大。在拆除区域边缘,导角区域顶板截面压应力增大至4.5～7 MPa。局部出现应力集中,导角两角点压应力达到9.0 MPa;阶段4,通过补强后,新浇桥面板及加强部分投入工作,共同承担二期恒载及运营荷载。原有结构顶板压应力普遍增加3 MPa左右,导角处局部应力为12.5 MPa,见图3(a)-(c)。

(2)新浇桥面板在二期恒载及运营荷载作用下,纵向应力均为压应力,上表面应力4.5～6 MPa,下表面压应力2 MPa左右。新增补强部分压应力0～ 3 MPa,见图3(d)-(e)。

图3 纵向应力云图

3.2 各阶段横向应力

开裂区左侧截面各阶段横向应力云图如图4所示。从图中可以看出:

(1)阶段1,在设计截面情况下,截面顶板压应力3～6 MPa,腹板内侧部分区域及底板底部有0.8 MPa左右的拉应力;阶段2,部分顶板退出工作,退出部分,应力变为0,而剩余顶板应力变大,在顶板梗腋附近压应力增加至7 MPa左右,导角角点处的压应力达到18.4 MPa。同时由于横向刚度减小,导致底板拉应力增大。顶板底部与底板底部有1.2 MPa左右的横向拉应力;阶段4,通过补强后,补强部分与原有拆除部分重新投入工作,老混凝土应力没有明显变化,见图4 (a)-(c)。

(2)新浇混凝土顶板上部翼缘部分出现拉应力,应力大小1 MPa以内;顶板底部加强部分出现拉应力,应力大小1 MPa左右。见图4(d)-(e)

图4 横向应力云图

3.3 主压应力

图5给出了压裂区段的主压应力图。从图中可以看出,阶段2,导角处最大主压应力21.4 MPa;阶段4,导角处最大主压应力21.7 MPa。两者相差很小,分析其主要原因为:主压应力的主要贡献来自于横向应力,而横向应力在阶段2与阶段4没有发生太大的变化,因此,主压应力在这两个阶段相差很小。

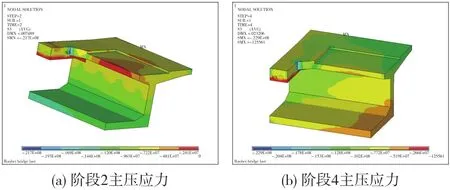
图5 主压应力云图

3.4 主拉应力

图6为开裂区主拉应力。从图中可见:阶段2腹板外侧主拉应力最大1.31 MPa,底板最大1.24 MPa,腹板内侧近上梗腋处2.2 MPa;阶段4腹板外侧主拉应力最大1.33 MPa,底板最大1.6 MPa,腹板内侧与顶板交界处最大主拉应力2.41 MPa。拉应力区域主要位于腹板内侧近上梗腋处、腹板外侧及底板底面。腹板外侧拉应力主要由横向预应力产生,由于阶段2,腹板内侧加撑,使得腹板没有较大的横向变形,而阶段4虽然拆除撑,但新浇顶板已参与受力,所以两阶段应力变化很小。底板底部主要由自重、二期恒载等荷载产生,而腹板内侧上梗腋处拉应力则主要是由竖向应力产生,即顶板的剪应力产生。它们均会随着荷载的加大而加大,阶段2至阶段4有0.2 MPa左右的增量。

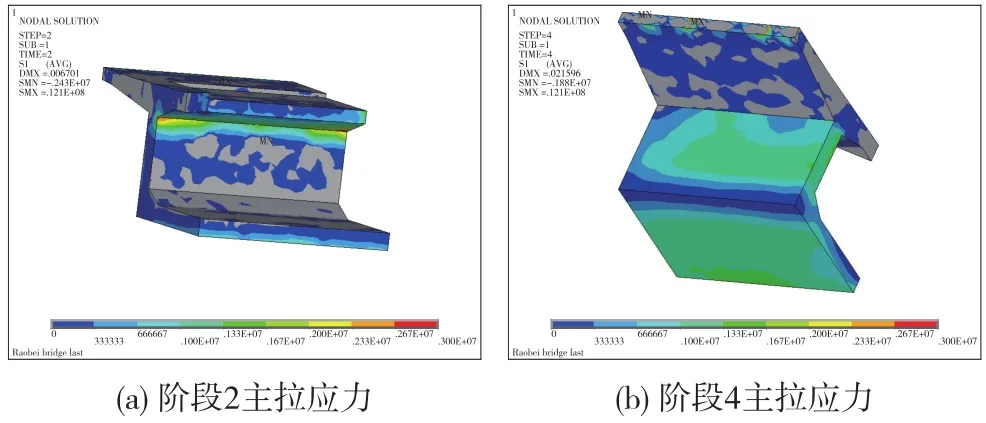
图6 主拉应力

4 结论

(1)阶段1至阶段2,即顶板部分拆除,剩余顶板结构纵、横向应力均增大,普遍增量3 MPa左右,局部增幅更大,角点处出现应力集中。

(2)纵、横应力从阶段2到阶段4,变化规律不同。其中纵向应力,在二期恒载及活载作用下会继续增大,新、老混凝土均表现为压应力;而横向应力在二期恒载及活载作用下,老混凝土压应力变化不大,而新混凝土部分区域出现拉应力,量值大小普遍在1 MPa左右,由于补强后混凝土仅能按照普通钢筋混凝土设计,需注意横向配筋。

(3)无论纵、横向,在上梗腋拆除角点边缘会出现较大的压应力,尖端主压应力为21.7 MPa,但区域很小,可在拆除时适当采用措施,防止应力集中。

(4)腹板外侧、内侧上梗腋处及底板底侧有部分拉应力,但主拉应力范围均在3 MPa以内。

参考文献:

[1] 姚玲森.桥梁工程[M].北京:人民交通出版社,1985.

[2] 徐岳,邹存俊.连续梁桥[M].北京:人民交通出版社,2012.

[3] 李辉.大跨度连续刚构桥的病害原因分析及加固设计[J].铁道标准设计,2011(4):52-54.

[4] 郭丰哲,钱永久,李贞新.预应力混凝土连续刚构桥合龙段底板崩裂原因分析[J].公路交通科技,2005,22(10):68-70.

[5] 张玉文.大跨度双线无砟轨道预应力简支箱梁梁端锚固区应力分析[J].铁道标准设计,2010(4):29-32.

[6] 宁贵霞,蔺鹏臻,孔德艳.双线铁路箱梁进人孔的局部应力分析[J].铁道标准设计,2005(10):63-64.

[7] 田仲初,陈耀章,赵利平,等.连续钢梁顶推过程局部接触分析及改善措施[J].长安大学学报:自然科学版,2012,32(4):44-50.

[8] 郑江,葛洪鹏,王先铁,等.局部位形约束生死单元法及其在施工力学分析中的应用[J].建筑结构学报,2012,33(8):101-108.

[9] 张立明.Algor、Ansys在桥梁工程中的应用[M].北京:人民交通出版社,2003.

[10]龚曙光,谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工作出版社,2004.

[11]郝文化.ANSYS土木工程应用实例[M].北京:中国水利水电出版社,2005.

[12]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

[13]陈艳.贵广铁路大跨预应力混凝土连续梁端部局部应力分析[J].铁道标准设计,2013(2):57-60.

Analysis on Local Stresses of Continuous Girder in Process of Top Slab Being Crushed and Restored

JIAN Fang-liang,LI Hui,HU Guo-hua,LI Hao
(China Railway Engineering Consulting Group Co.,Ltd.,Beijing 100055,China)

In this study,by comprehensively using the element birth and death technique as well as the multi-step solving technique of ANSYS software,a refined solid finite element model was established, and the local stress distribution and variation were analyzed for a certain continuous girder in the process of its top slab being crushed and restored.The results showed that:(a)after part of crushed top slab were removed,the longitudinal stress and the transverse stress in the rest of the top slab were generally increased by 3 MPa or so,while the phenomenon of stress concentration occurred at the local corner points;(b)after repairing and strengthening the top slab,the longitudinal stress of older concrete continued to increase because of the action of the secondary permanent load and live load,while the transverse stress of older concrete was not changed basically;(c)before and after bearing the secondary permanent load and live load,both the maximum principal compressive stress and maximum tensile stress were little changed,but the maximum principal compressive stress at the stress concentration points of the structure had reached up to 21.7 MPa,which should be taken into account.

continuous gird;element birth and death;local stress

U441+.5

A

10.13238/j.issn.1004-2954.2014.04.010

1004-2954(2014)04-0044-04

2013-07-30

简方梁(1982—),男,工程师,2012年毕业于同济大学桥梁工程专业,工学博士,E-mail:jfl8223_2003@163.com。