多阶段复合期权模型在新药研发中的应用研究

骆 桦，徐 舒

（浙江理工大学理学院，杭州310018）

多阶段复合期权模型在新药研发中的应用研究

骆 桦，徐 舒

（浙江理工大学理学院，杭州310018）

考虑到新药研发周期长和高度的不确定性的特点，在实物期权理论的基础上建立了多阶段复合期权的评价模型，针对二阶段定价模型的不足，提出了各阶段波动率不同的三阶段定价模型，并得到其封闭解。最后用改进的三阶段变波动率复合期权模型来评估一个新药研发项目的价值，计算结果表明模型具有较好的实用性。

多阶段复合期权；新药研发；变波动率；应用研究

0 引 言

复合期权顾名思义表示的是期权的期权［1］，它是以普通期权为标的资产，而且有多个执行价格和到期时间。在研究复合期权之前，Black和Scholes得出了金融期权定价的模型，这为复合期权的研究奠定了基础。随后，Geske研究了两期复合期权模型并求解了它的封闭解的形式［2-3］，从此以后复合期权模型才得以广泛应用。复合期权的本质表示的是权利之间的嵌套，它比较适合应用于序列决策的问题。现在很多R&D项目都具有多阶段的特性，它们的前提条件是只有在前期的研究目标达到时才能进入下一期的研究［4］。目前，关于复合期权的理论、方法与应用研究是众多学者关注的热点。

本文首先对二阶段复合期权模型给出了一个新的证明，主要采用由一维标准正态分布函数推导出二维标准正态分布函数的思想。其次，在新药研发过程中，假设波动率是一个固定常数的模型，在实际运用中显然是不太合理的，所以本文在多阶段复合期权模型中引入了变波动率，使得模型具有较强的适应性。最后给出模型在新药研发评价上的一个应用，结果表明这种改进方法是比较有价值的。

1 三阶段复合期权定价模型

在新药研发过程中，投资者在每一阶段所拥有的投资权利可以看成一个期权，由于第一个期权导致了第二个期权的产生，因此整个项目是一个复合期权。依次类推，可以得到新药研发的三阶段复合期权过程如图1所示。

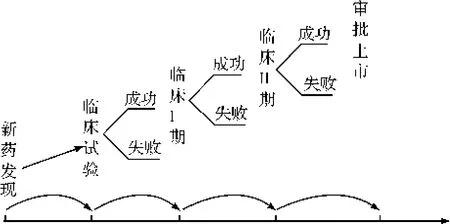
图1 新药研发多阶段复合期权形成示意

设资产价格Vt遵循几何布朗运动：

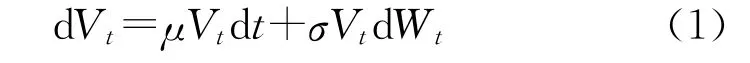
其中，Wt是标准布朗运动，μ和σ分别是资产价格的漂移率和波动率。设F（Vt，t）代表由标的资产Vt衍生出来的金融工具价格，其是一阶连续可微的。这里设F（Vt，t）=ln Vt，则有：

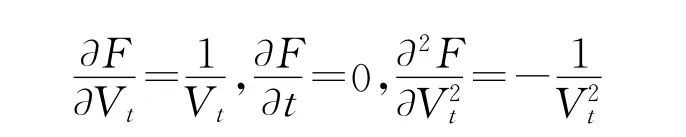
应用Ito引理可用得到：

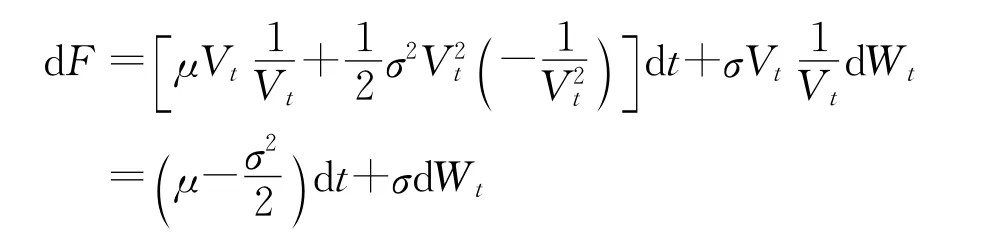
即

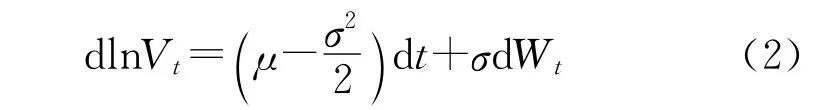
对上式两边积分可以得到资产价格的表达式为：

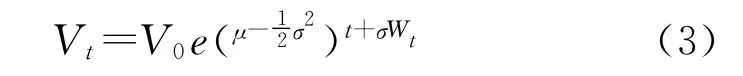
新药研发的价值一般是由初始投资产生的未来投资机会的价值决定的，而不是由投资产生的现金流来决定的。设初始投资额为V0，到期时间为T0，第一阶段的投资额为I1，到期时间为T1，在T1时刻产生的现金流折现的现值为VT1，这样新药研发过程就产生了第一个期权，所以在T1时刻项目收益率为max｛VT1-I1，0｝，则由（3）得：

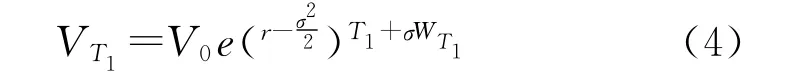
其中WT1是均值为0、方差为T1的正态随机变量。上式在等鞅测度下成立，Y是无风险利率。

若F1（V，0）表示0时刻的投资机会，可以用Z代替上述WT1，其中Z是标准正态变量（均值是0、方差是1）［5］，则有：

其中 N1（·）表示标准正态分布，h1=

如果在T1时刻第一个期权得以执行，即临床I期实验成功了，那么在T2时刻将获得临床II期试验的机会，这样就形成了第二个期权，其中，到期时间为T1=T2+τ1，执行价格为进行临床试验所需的投资额I2。在这一过程中存在两个期权，且第一个期权导致第二个期权的产生，而且只有在第二个期权的价值比第一个期权的执行价格大时，复合期权可得以执行，这个过程就是一个复合期权，所以在T2时刻复合期权收益为：

所以在0时刻复合期权价值为0时刻的贴现值：

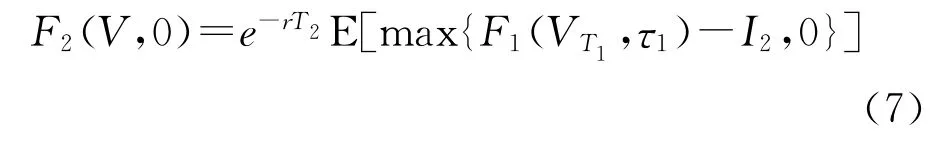
其中F1（VT2，τ1）=VT2N1（h1（VT2，τ1））-I1e-rτ1 N1（l1（VT2，τ1））。

综合上述说明，可得二阶段复合期权定价模型如下：

定理1 假设无风险利率r和波动率σ都是已知的常数，资产价格Vt服从几何布朗运动，则二阶段复合期权定价模型为：

其中u2=inf｛u∈R｜F1（VT2，τ1）≥I2｝，

证明 假设Y在X下的条件分布为f（y｜x），μY｜X=α+βx，=σ2，设X的均值为μX，方差为，则X与Y的联合密度函数为［6］：

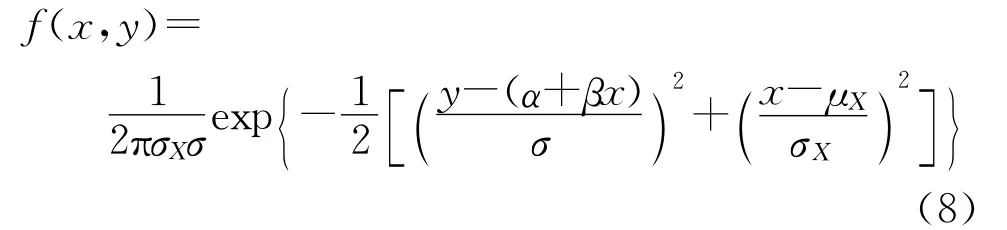
其中-∞＜x＜+∞，-∞＜y＜+∞。

假设随机变量Y可以写成如下形式：Y=α+βX +ε，其中α，β是常数，ε是均值为0方差为σ2的随机误差项，与X相互独立，则：

用上述α、σ的值代入（8）式中的f（x，y），则二维正态分布为：

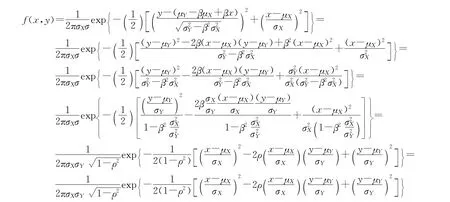
此外若X～N（0，1），Y～N（0，1），则μX=μY= 0，σX=σY=1，由此得到二维标准正态分布：

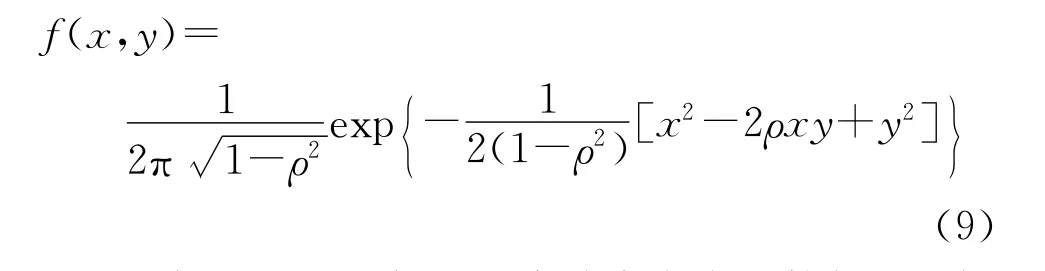
根据以上一维标准正态分布密度函数与二维标准正态分布密度函数之间的这种关系，可得如下结论：对于F2（V，0）中的第一项：

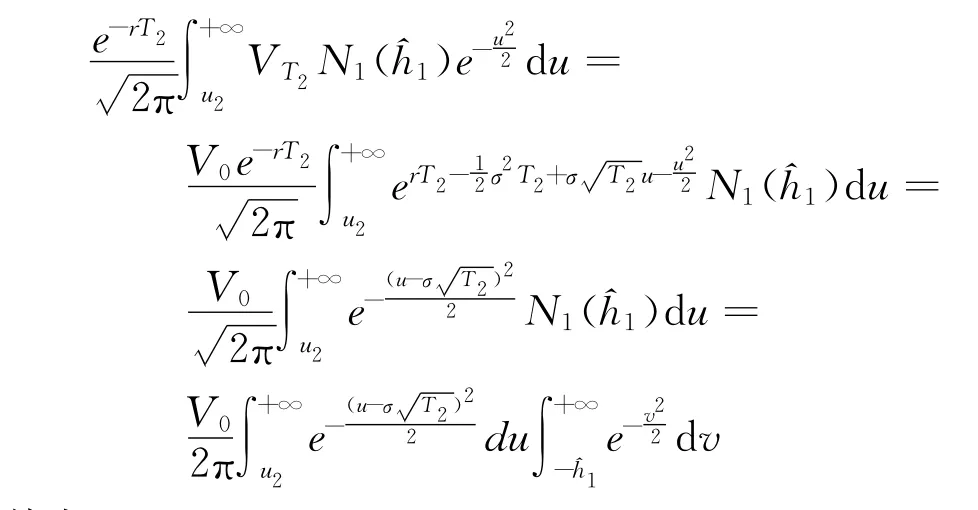
其中，

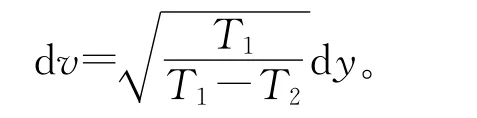
因为v的取值范围为［-ˆh1，+∞），所以当v=-ˆh1时，则有：

所以

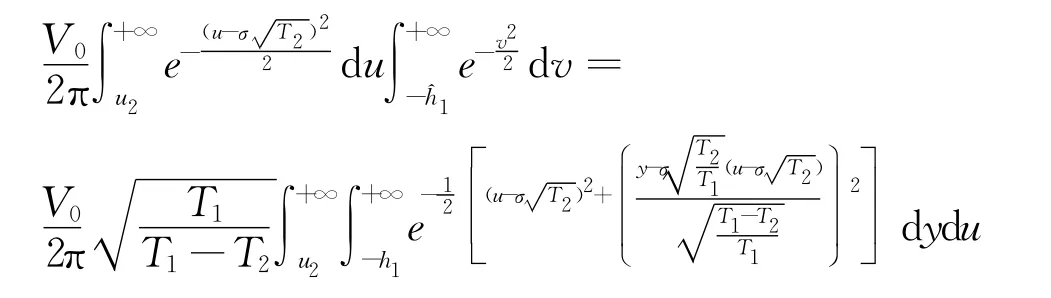
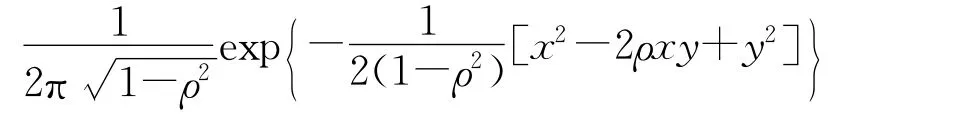
在表达式

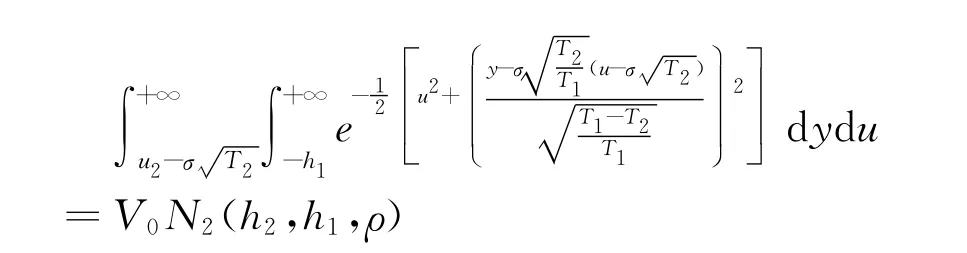
因为u2=inf｛u∈R｜F1（VT2，τ1）≥I2｝，所以u2是F1（VT2，τ1）-I2=0的临界值，假设满足方程F1（VT2，τ1）-I2=0，则有：

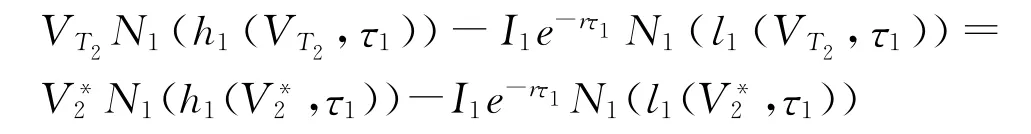
那么

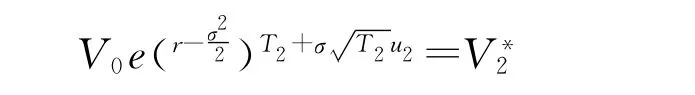
由上述方程解得：

则

同理，对于F2（V，0）的第二项也采取类似的方法得到：

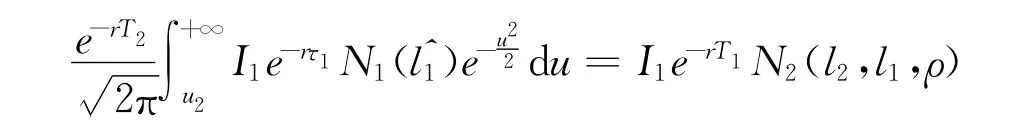
所以F2（V，0）最终的表达式为：

其中，

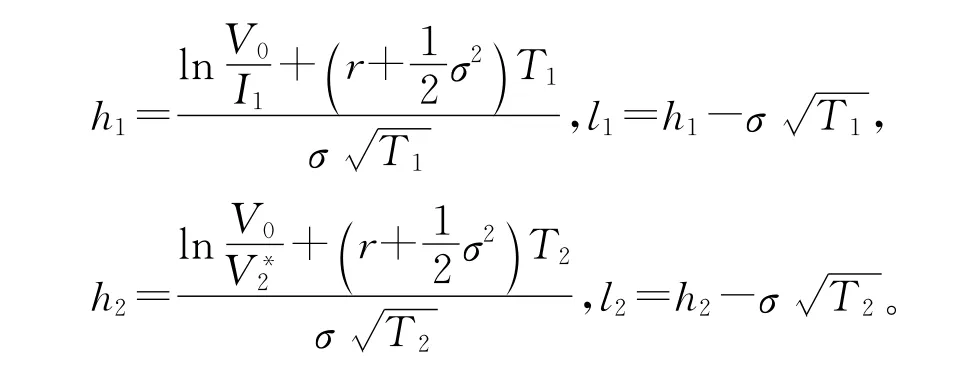
注：以上证明过程主要利用二维正态分布的一些性质，相比Cassiimon［7］利用格林函数和delta函数来证明要简洁明了一些。

2 变波动率的多阶段复合期权模型

以往的文献［2-3］在新药研发评价中假定波动率是常数，这种假设是不太符合实际情况的。因为新药研发在每个阶段的任务和目标都不一样，所以它在每一个阶段的风险价值也不同，因此，每一阶段的波动率应该是不一样的。在这种情况下，本文对原有模型进行了改进，在每一阶段引入了可变的波动率，使得模型更具有适应性。综合上面的分析，可得以下复合期权模型：

定理2 三阶段的复合期权模型为：

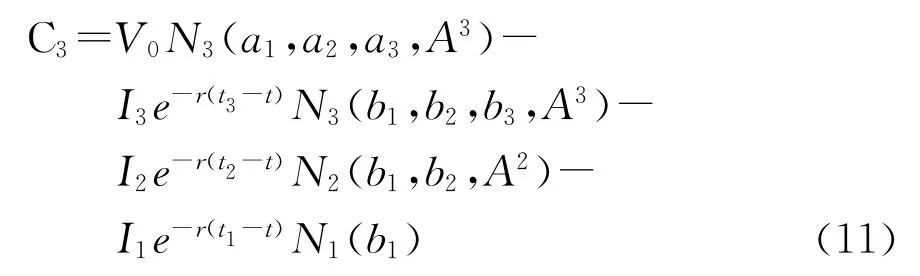
其中

σ1，σ2，σ3表示三阶段中每一阶段的波动率。=I3，

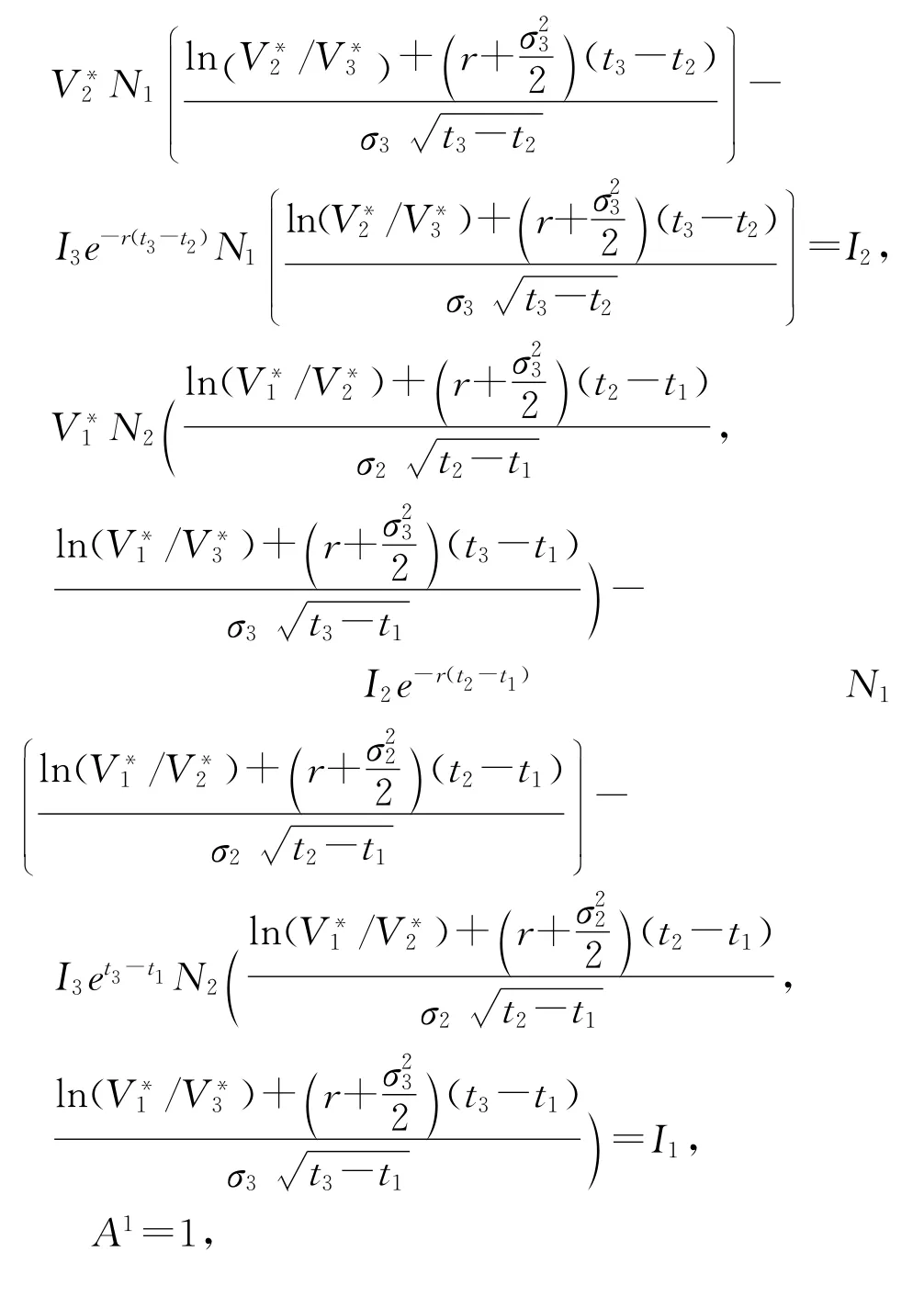
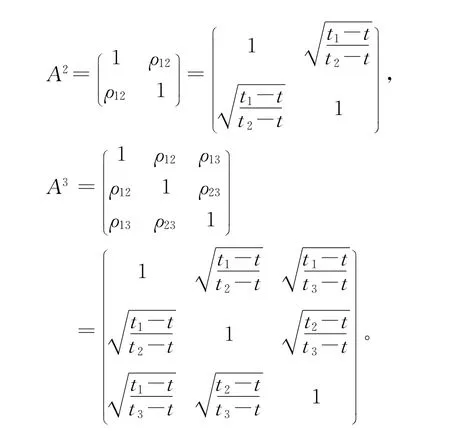
证明 期权价格C3满足下列偏微分方程：

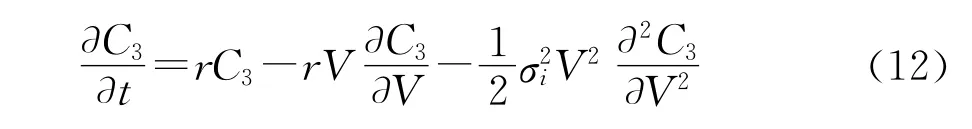
该偏微分方程在ti时刻满足的边界条件是Ci（V，ti）=max（0，Ci+1（V，ti）-Ii），是非线性方程Ci+1，ti）=Ii的解。

偏微分方程（12）可以转化为：

关于新变量p和s的边界条件调整为：

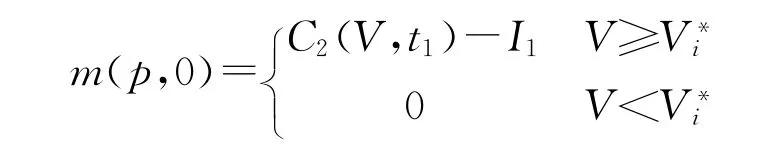
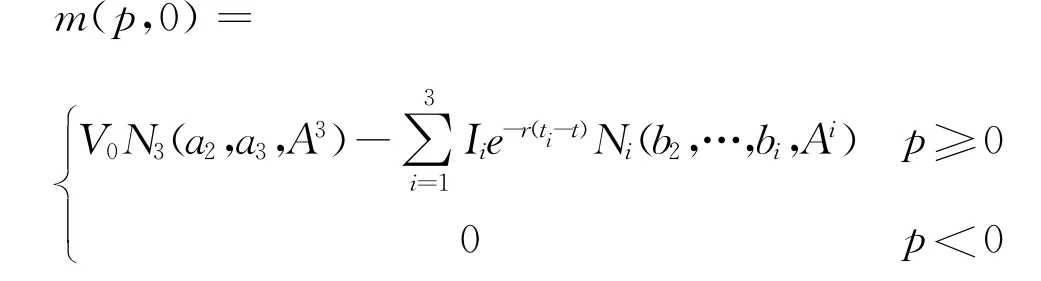
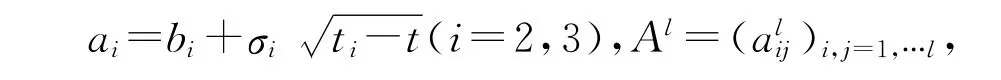
经过上述变量替换，可以得到在t=t1时，资产价格V的表达式为：

则

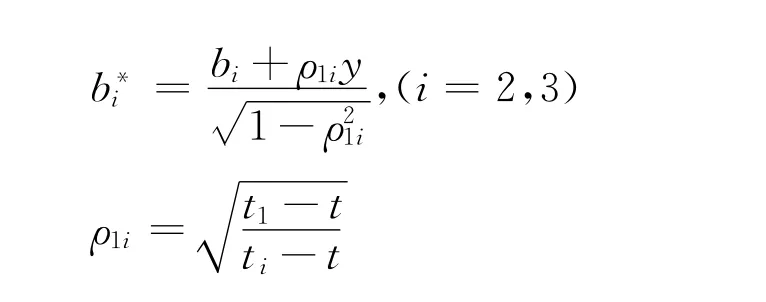
因为

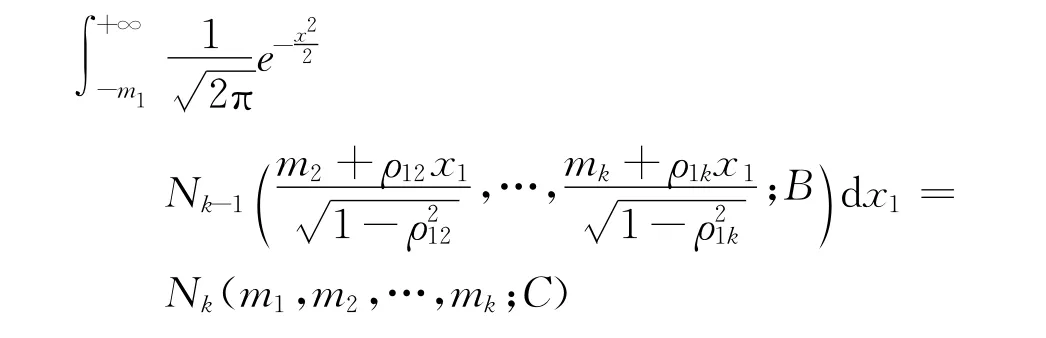
其中

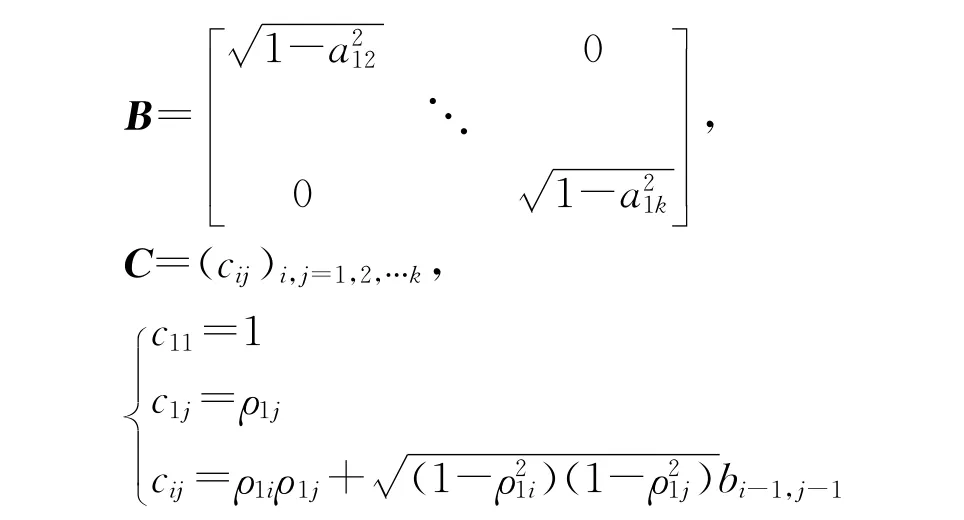
所以

其中，

最后得到3阶段复合期权模型为：

其中，

σi表示三阶段中每一阶段的波动率；

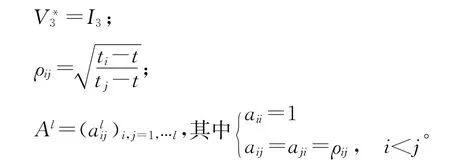
定理证毕。

3 算法和应用实例

新药研发是一项风险高、不确定性高、阶段多的投资项目。像这种多阶段投资决策的问题需要采用特殊的实物期权模型---多阶段复合期权模型来描述［8］。正由于新药研发具有这种特殊的投资模式，所以传统的二阶段、常波动率的复合期权模型是不适用的，而本文所研究的变波动率、三阶段复合期权模型为新药研发提供了更为合理的评估方法，下面通过实例说明如何应用本文给出的模型。

某新药研发公司现要进行一项新药的研究项目，需要评价该项目的价值，然后决定是否投资。该项目每个阶段所花时间年数为t1=3，t2=5，t3=6，其中t0=0，各阶段的投资成本I1=300万元，I2= 550万元，I3=1 200万元，初始投资V0=9 000万元，无风险利率r=3.5%，将这些参数代入三阶段复合期权模型：

关于各阶段波动率σi的计算采用专家打分和理论计算相结合的方式，具体计算方法参考文献［9-10］的方法，其中，V0=9 000，Zi为各阶段假设项目价值，其他的变量数据见表1。

表1 各变量数据

表2 各阶段临界值和三阶段期权价值

当波动率为某一固定常数时，通过计算发现，当σ=0.9时（新药研发往往波动率比较大），期权价值是4 086.68万元，用改进的模型计算得到2 909.65万元，两者相比发现，波动率为固定常数的模型明显高估了期权的价值，会给投资者造成错误的判断。

4 结 论

从上面分析可见，复合期权主要描述了在不确定条件下投资决策过程中的一系列的相关权利，而这些权利的作用就是使得整个决策过程更加地灵活，所以复合期权的理论和方法在分析多阶段投资决策问题方面具有很大的优势。在新药研发过程中，如果使用传统的常波动率复合期权模型就会存在很多缺陷，而本文是在多阶段复合期权模型中加入变波动率，得到的模型就具有较强的适应性，也给投资者提供了一个比较可靠的评价工具。

［1］Kwok，Y.W.Mathematical models of financial derivatives［M］.New York：Springer，2008：1-3.

［2］Geske R.The valuation of corporate liabilities as compound options［J］.Journal of Financial and Quantitative Analysis，1977，12（4）：541-552.

［3］Geske R.The valuation of compound options［J］.Journal of Financial Economics，1979，7（1）：63-81.

［4］Lee J，Paxson D A.Valuation of R&D real American sequential exchange options［J］.R&D Management，2001，31（2）：191-201.

［5］斯塔夫里，古德曼.金融数学［M］.蔡明超，译.北京：机械工业出版社，2004：85-88.

［6］Walpole.Probability&Statistics for Engineers&Scientists［M］.London：Pearson Education.2007：179-190.

［7］Cassimon D，Engelen P J，Thomassen L，et al.The valuation fo a NDA using a 6-fold compound option［J］. Research Policy，2004，33（1）：41-51.

［8］龚 朴，何志伟.变波动率多期复合实物期权定价模型及应用［J］.管理工程学报，2006，20（2）：46-53.

［9］Arnold T，Shockley R L.Value creation atanheuserbusch：a real options example［J］.Journal of Applied Corporate Finance，2001，14（2）：52-61.

［10］Shockley R.An Applied Course in Real Options Valuation［M］.New Zealand：Thomson South-Western. 2007：523.

［11］袁亚湘.非线性优化计算方法［M］.北京：科学出版社，2008：88.

Research on AppIication of MuIti-stage Compound Option ModeIin New-Drug Research and DeveIopment

LUO Hua，XUShu
（School of Sciences，Zhejiang Sci-Tech University，Hangzhou 310018，China）

Considering the characteristics of long period and high uncertainty of new drug research and development，we establish a multi-stage compound option evaluation model based on real option theory to improve the shortcomings of the pricing model in the first and second stages.Besides，we propose threestage pricing model with different volatilities in each stage and gain the closed-form solution.Finally，we use the improved three-stage compound option model to evaluate the value of a new drug research and development project.The results show that the model has excellent practicability.

multi-stage compound option；new drug research and development；varied volatility；applied research

F830.59

A

（责任编辑：许惠儿）

1673-3851（2014）05-0539-07

2013-10-16

国家自然科学基金（60903143）

骆 桦（1962-），男，浙江诸暨人，硕士，副教授，主要从事金融数学的研究。

骆 桦，E-mail：luohuahill@163.com