单纤维对惯性颗粒稳态过滤捕集效率的数值模拟分析

杨 林，付海明，李 杰，王 亮

（东华大学 环境科学与工程学院，上海 201620）

单纤维对惯性颗粒稳态过滤捕集效率的数值模拟分析

杨 林，付海明，李 杰，王 亮

（东华大学 环境科学与工程学院，上海 201620）

采用计算机对单纤维稳态过滤捕集效率进行模拟分析，所选研究对象为惯性单分散颗粒，模拟分析中考虑拦截机理及碰撞机理作用，同时忽略扩散机理的影响.采用Kuwabara流场来表征单纤维表面的气流绕流特征，以计算粉尘颗粒运动的轨迹，计算分析了斯托克斯数St、拦截系数R及填充率c对稳态单纤维捕集效率的影响.研究结果表明：单纤维稳态过滤捕集效率均随St、R及c的增大而增大，单纤维稳态过滤捕集效率与填充率近乎呈线性增加的关系.模拟计算结果与文献研究结果基本吻合.

单纤维；捕集效率；数值模拟；空气过滤；稳态过滤

工业生产、汽车尾气及自然作用产生的大量微粒影响着大气环境［1］，使得空气中含有大量的有害气体和细小的悬浮颗粒物，这对人类的呼吸免疫功能、呼吸道、心血管和中枢神经系统等造成了严重的危害［2］.纤维过滤器是减少大气污染的高效方法之一，其在工业生产中发挥着重要作用［3-4］.因此，纤维过滤理论及技术的研究是一项重要的研究课题［5］.单纤维过滤捕集效率是研究纤维过滤理论及技术的主要内容之一，对纤维过滤理论的发展起着至关重要的作用.

多年来，国内外许多学者对单纤维过滤捕集效率进行了大量的研究，但对单纤维的碰撞、拦截及扩散捕集机理如何合并计算，一直存在很大的问题和争议.单纤维的碰撞、拦截及扩散捕集机理实际上是同时存在的，对于不同粒径的颗粒，其捕集机理所起的作用大小不同.对于粒径较小的颗粒，其惯性碰撞捕集机理较小，可以忽略不计；而对于粒径较大的颗粒，其扩散捕集机理较小，可以忽略不计.由于受计算条件的限制，对于单纤维的碰撞、拦截及扩散捕集机理的计算大多数是分别进行的，然后采用相叠加的原理或按其穿透率相乘原理进行组合，此两种计算方法计算结果存在较大的差距，两种方法均存在一定的问题.

本文针对惯性颗粒，在不考虑其扩散机理的条件下，采用Kuwabara流场［6］计算单纤维周围流场及颗粒运动轨迹.假设颗粒接触纤维即被捕集，忽略尘滤尘机理对单纤维捕集效率的影响，采用文献［7］提出的随机模拟方法，同时考虑拦截机理与碰撞机理的共同作用，创建模拟单纤维捕集效率虚拟实验平台.模拟分析稳态单纤维过滤介质表面对粉尘颗粒的捕集，并详细讨论斯托克斯数、拦截系数、填充率对单纤维捕集效率的影响.本文旨在探讨研究单纤维捕集效率模拟计算的新途径.

1 模拟描述

1.1 模型的建立

Kuwabara单纤维模型［8］用于分析纤维过滤介质表面尘粒捕集问题.单纤维捕集机理模型如图1所示，较为形象地描述了3种捕集机理的捕集颗粒行程.

图1 单纤维捕集机理图Fig.1 Single fiber collection mechanism

模拟过程中，由控制面随机产生的粉尘颗粒在流动阻力作用下向纤维运动.通过计算颗粒运动的轨迹来确定粉尘颗粒是否与纤维发生碰撞，若发生碰撞，则粉尘颗粒被纤维表面所捕获，即粉尘颗粒被惯性碰撞机理所捕集；若颗粒沿流场流线运动，且颗粒质心到纤维中心的距离等于颗粒半径与纤维半径之和，则此时即为拦截机理捕集颗粒；如颗粒既未发生碰撞且颗粒质心到纤维中心的距离也不等于颗粒半径与纤维半径之和，则粉尘颗粒继续运动，此时颗粒被认为没有被捕集［8］.

而现实的粉尘颗粒在纤维过滤器内的沉积过程很复杂，本文为了获得明确的模拟结果，作如下基本假设：

（1）忽略已沉积颗粒对后期颗粒沉积的影响；

（2）粉尘颗粒不受电场力、重力及其他力的影响；

（3）假设颗粒为惯性颗粒，忽略颗粒的布朗运动；

（4）忽略颗粒对流场及粉尘颗粒运动轨迹的影响；

（5）忽略粉尘颗粒因反弹逃离单纤维表面而未被捕集等因素的影响；

（6）忽略粉尘颗粒间相互作用力对粉尘颗粒运动产生的影响.

1.2 模型中的颗粒运动轨迹

本文对颗粒运行的轨迹描述主要是通过牛顿第二定律进行计算描述并最终表示，详见文献［9］.

2 数值计算与结果讨论

2.1 稳态单纤维捕集效率计算

本文不考虑已沉积颗粒对后期来流颗粒沉积的影响，仅由纤维体本身对颗粒进行捕集，捕集体的形状永远都是这根纤维，因此，基于极限轨迹的单纤维捕集效率计算方法在这里是恒定适用的.令t时间内通过控制面的颗粒数为N，其中被捕集的颗粒数为N0，则稳态单纤维捕集效率η0的计算式可表示为

文献［10］采用实验的方法测试洁净纤维的捕集效率，实验测试中所拍图片如图2（a）所示.本文模拟结果如图2（b）所示.

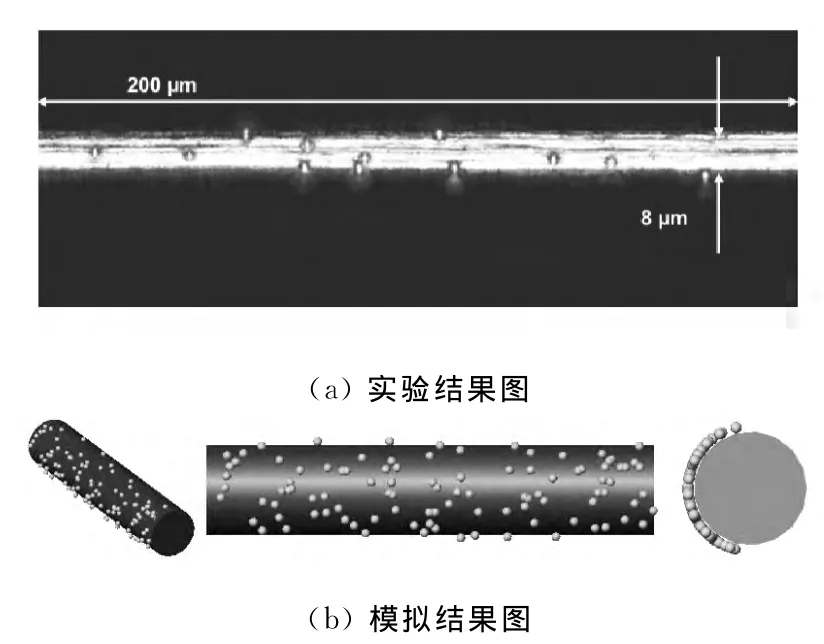
图2 模拟结果与文献实验结果对比Fig.2 The simulation results compared with the experimental results

2.2 结果与讨论

2.2.1 模拟计算结果稳定性分析

本文所讨论的为颗粒直径dp≥0.5μm的情形，并忽略其他各外力场的影响，因此，这里的颗粒捕集机理为惯性碰撞和拦截效应.数值求解过程中，颗粒的运动时间步长为Δt＝0.05.计算过程中所需的基本参数：空气动力黏度μ为1.8×10-5Pa·s；单纤维过滤模型的纤维直径为10μm；纤维长度为50μm.气流中颗粒分布的随机特征决定了每次模拟结果必为一次随机事件，因此，在相同计算条件下执行多次模拟结果取平均值才具有统计意义.

图3所示为稳态单纤维捕集效率随取平均值的数据组数的增加而变化的趋势图.由图3可知，在模拟次数重复均在10次以内的捕集效率平均值已趋于稳定，因此，在本文的计算中，每种计算条件下执行10次重复模拟，然后对计算结果取平均值.

图3 捕集效率平均值随数据组数增大而变化的趋势图Fig.3 The average value of collection efficiency changes with the number increasing of data sets

2.2.2 斯托克斯数St对稳态单纤维捕集效率的影响

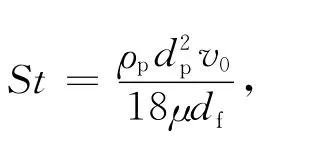
式中：ρp为颗粒密度，kg／m3；dp为颗粒直径，m；v0为过滤风速，m／s；df为纤维直径，m.

针对η0选取一个参数范围和条件等都合适的表达式（式（2））与模拟实验进行参照对比.

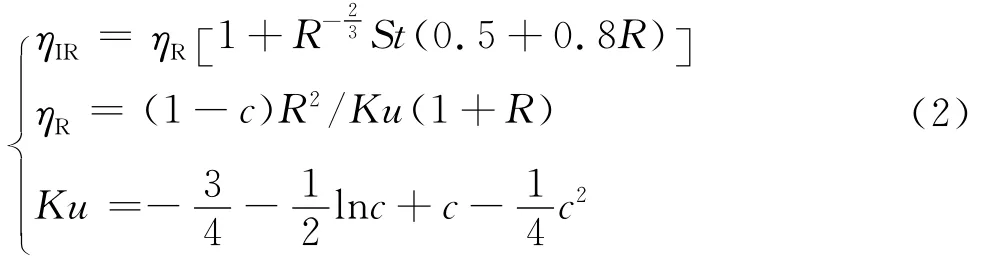
式中：R＝dp／df为拦截系数；ηR为拦截机理作用下的捕集效率；ηIR为碰撞和拦截两个机理共同作用下的捕集效率；c为填充率.

计算机模拟计算过程中所取参数：颗粒直径dp＝1μm，纤维直径df＝10μm，纤维长度Lf＝5df＝50μm，填充率c分别为0.05和0.15，斯托克斯数St作为x轴在0.3～2.5取15个点进行采样计算.模拟计算结果如图4所示.

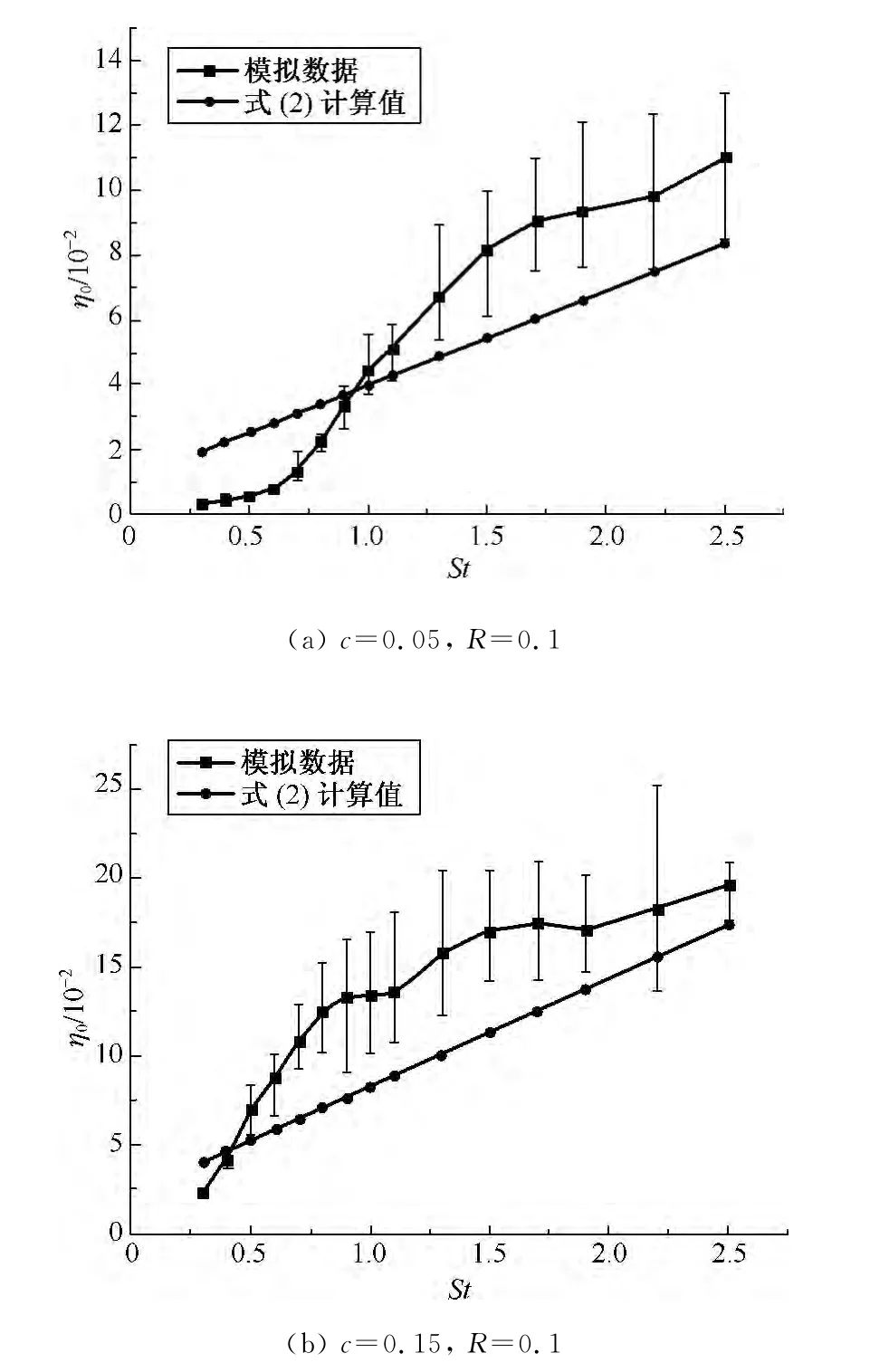
图4 η0与St之间的变化关系图Fig.4 Relationship betweenη0 and St

图4中的模拟数据线为误差图表示方式，上下点分别为模拟计算中该组捕集效率值中的最大值与最小值，从而体现了颗粒运动的随机性.由图4可知，随着St的增大，捕集效率η0整体呈现明显的递增过程，说明稳态情况下（忽略颗粒沉积在单纤维上沉积数量的增长），或非稳态情况下的颗粒沉积初始阶段，St对颗粒的捕集起着决定性的作用，这与经典纤维过滤理论的结论吻合［11］.

2.2.3 拦截系数R对稳态单纤维捕集效率的影响

模拟计算过程中所取参数：纤维直径df＝10μm，纤维长度Lf＝5df＝50μm，斯托克斯数St＝1，填充率c分别为0.05和0.15，拦截系数R作为x轴在0.005～0.800取15个点进行采样计算.计算过程中，通过改变颗粒直径的大小来改变拦截系数的值.模拟数据及经验计算式下拦截系数R对稳态单纤维捕集效率的影响关系曲线如图5所示.

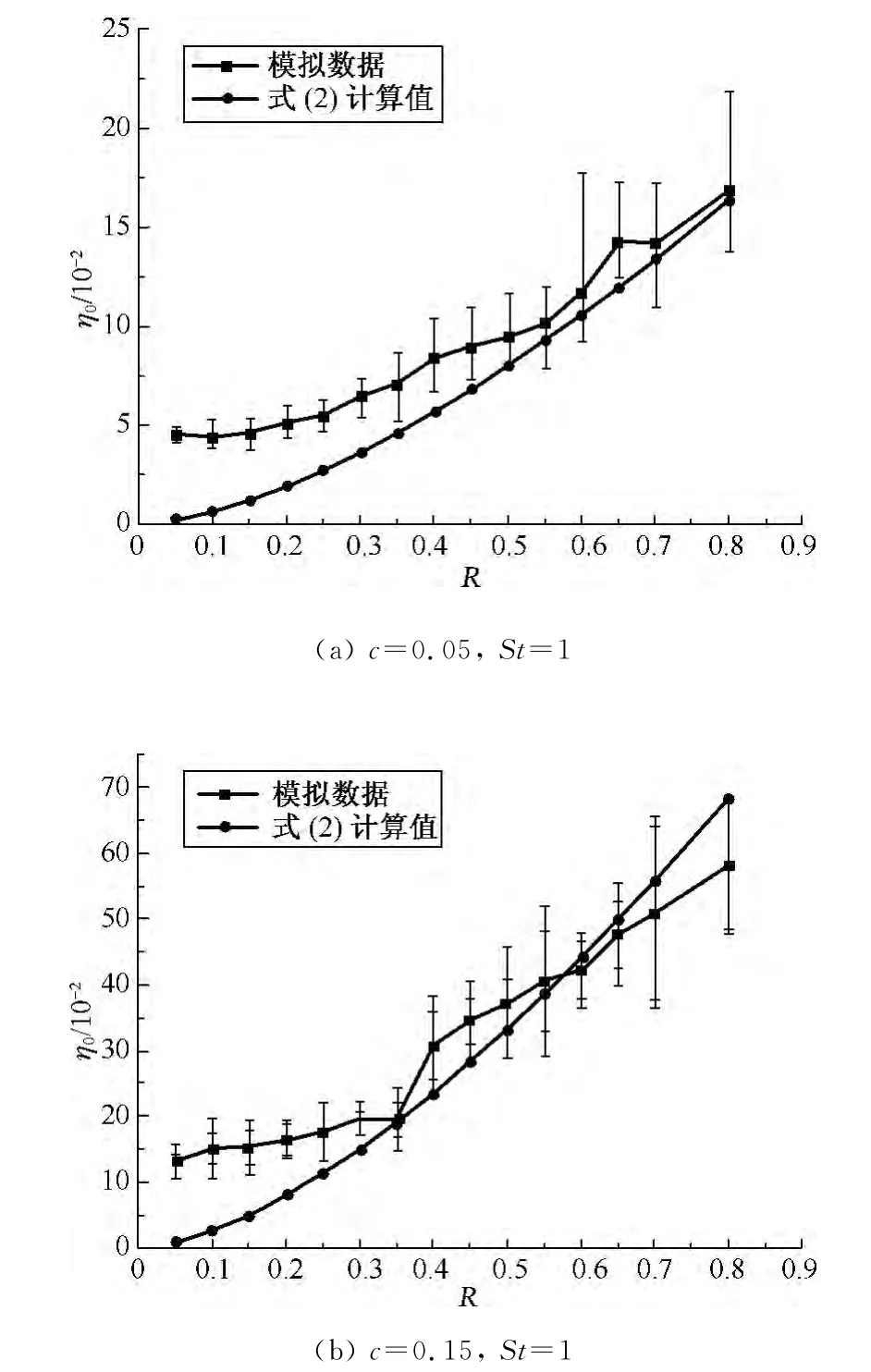
图5 η0与R之间的变化关系Fig.5 Relationship betweenη0 and R

由图5可知，捕集效率η0随拦截系数R的增大总体是逐渐增加的，且近似呈抛物线增加，其变化趋势与式（2）计算结果基本一致.这说明，稳态及非稳态的初始阶段，拦截系数R对颗粒的捕集同样具有显著的影响作用.

2.2.4 填充率c对稳态单纤维捕集效率的影响

模拟计算过程中所取参数：颗粒直径dp＝1μm，纤维直径df＝10μm，即拦截系数R＝0.1，纤维长度Lf＝5df＝50μm，St分别取0.5和1，填充率c在0.001～0.300取15个点进行采样计算.填充率c和稳态单纤维捕集效率之间的关系曲线如图6所示.

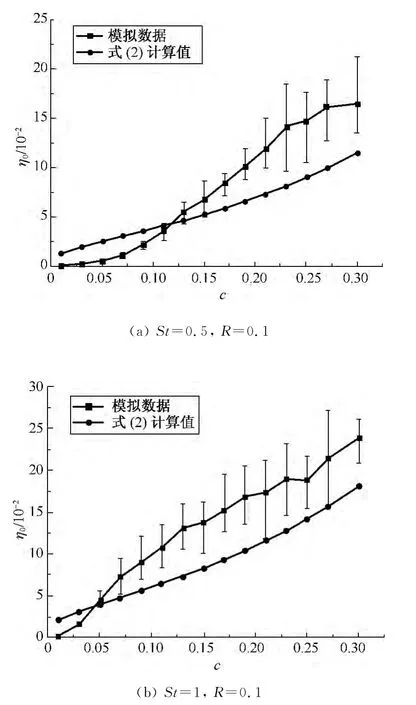
图6 η0与SVF之间的变化关系Fig.6 Rrelationship betweenη0 and SVF

由图6可知，填充率c对捕集效率η0的影响是非常明显的.随着c的增大，η0近似呈线性增加，其变化趋势与式（2）计算结果基本一致.

由图4～6可知，斯托克斯数St、拦截系数R及填充率c对稳态单纤维捕集效率η0均存在较大的影响，它们可被视为单纤维稳态过滤的主要影响因素，单纤维稳态过滤捕集效率可被描述为

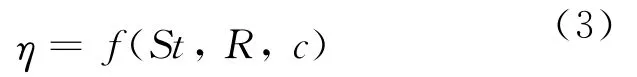
描述惯性颗粒的单纤维稳态过滤拦截及碰撞机理作用的捕集效率数学模型具体表达式有待于进一步的研究.

3 结 语

本文在不考虑颗粒沉积、颗粒间相互作用及其他一切外力影响的前提下，采用计算机模拟的方法对稳态情况下的单纤维过滤介质表面颗粒的沉积进行了模拟，分析其捕集效率受斯托克斯数St、拦截系数R及填充率c的影响规律.研究结果表明：St、R及c对稳态单纤维捕集效率均具有显著的影响作用，随着St、R及c的增大，稳态单纤维捕集效率η0均是递增的，而且捕集效率η0与R近似呈抛物线增加，与c则近似呈线性增加的关系.单纤维稳态过滤捕集效率可被描述为St、R及c的函数.研究结果与相关文献研究结果基本吻合.由此表明，本文的研究方法可以模拟拦截及碰撞机理对单纤维稳态捕集效率的作用，为研究及获得单纤维稳态捕集效率变化规律提供了条件及途径.从而避免了传统过滤理论采用繁琐及复杂的轨迹计算统计分析方法，孤立考虑拦截机理与碰撞机理作用，然后再将其机理合并计算所产生的误差及弊端，可以通过模拟计算，直接获得接近真实的、随机的捕集效率虚拟实验结果.

本文研究的重点主要集中在稳态情况下的单纤维对单分散颗粒的捕集模型，然而在实际过滤纤维捕集粉尘过程中，捕集的粉尘颗粒往往为多分散颗粒且颗粒分散度较大，同时，已沉积颗粒对纤维的进一步捕集有着非常显著的影响.因此，针对稳态单分散非惯性颗粒的捕集模型及非稳态情况下的多分散颗粒对纤维过滤捕集理论产生的影响及影响程度，这是今后需进一步深入研究的问题.

［1］MORAWSKA L，THOMAS S B，BOFINGER N D， et al.Comprehensive characterization of aerosols in a subtropical urban atmosphere：Particle size distribution and correlation with gaseous pollutants［J］.Atmospheric Environment，1998，32（14／15）：2461-2478.

［2］钱付平，王海刚.随机排列纤维过滤器颗粒捕集特性的数值研究［J］.土木建筑与环境工程，2010，32（6）：120-126.

［3］MOELTER W，FISSAN H .Structure of a high efficiency glass fiber filter medium［J］.Aerosol Science and Technology，1997，27（3）：447-461.

［4］KERSCHMANN R.Filter media structure in virtual reality［J］.Filtration and Separation，2001，38（7）：26-29.

［5］付海明，沈恒根.纤维过滤器过滤理论的研究进展［J］.中国粉体技术，2003，9（1）：41-46.

［6］KUWABARA S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers［J］.Journal of the Physical Society of Japan，1959，14（4）：527-532.

［7］WANG C S，BEIZAIE M，TIEN C.Deposition of solid particles on a collector：Formulation of a new theory［J］.Joumal of American Institute of Chemical Engineers，1977，23（6）：879-889.

［8］朱辉，付海明，亢燕铭.粉尘颗粒在单纤维表面沉积的计算机模拟［J］.环境污染与防治，2009，31（3）：10-15.

［9］朱辉，付海明，亢燕铭.单纤维过滤介质表面尘粒捕集的随机模拟［J］.环境工程学报，2010，4（8）：1881-1886.

［10］GERHARD K，STEFAN S，JORG M，et al.The collection efficiency of a particle-loaded single filter fiber［J］.Journal of Aerosol Science，2009，40（12）：993-1009.

［11］DAVIES C N.Air filtration［M］.New York：Academic Press Inc，1973.

Numerical Simulation Analysis of Stationary Collection Efficiency of Inertial Particles on Single Fiber Surface

YANGLin，FUHai-ming，LIJie，WANGLiang

（School of Environmental Science and Engineering，Donghua University，Shanghai 201620，China）

The collection efficiency on a single fiber in steady condition was mainly discussed with computer simulation data，and the inertial particles were taken as the research object.The interception mechanism and the inertial collision mechanism were taken into account during the simulation，at the same time particle dif fusion collection mechanism was ignored.Kuwabara flow field was used to characterize the airflow around the surface of single fibers so that the trajectory of particles could be calculated.The effect of Stokes numberSt，interception coef ficientRand the filling ratecon collection efficiency of single fiber was discussed.It was found that the collection efficiency increased withSt，Randcincreasing，and that its value approximately showed a linear increase relationship withcincreasing.The simulation results were consistent with the literature results.

single fiber；collection efficiency；numerical simulation；air filtration；stationary filtration

TQ 021

A

2013-04-03

国家自然科学基金资助项目（51178094）

杨 林（1989—），男，江苏盐城人，硕士，研究方向为纤维过滤原理.E-mail：yanglin＿leo＠sina.cn

付海明（联系人），男，高工，E-mail：fhm＠dhu.edu.cn

1671-0444（2014）03-0345-05