器件温度测试的影响因素

李兴鸿，赵春荣，赵俊萍

（北京微电子技术研究所，北京 100076）

器件温度测试的影响因素

李兴鸿，赵春荣，赵俊萍

（北京微电子技术研究所，北京 100076）

本文从器件用热像仪的测温过程、常用公式出发，针对测温条件进行了探讨，对公式里面的指数n的取值进行了推算。认为n可取4，但常数C和指数n的取值与波长范围和温度范围有关，要匹配。同时对IC温度分布的精确测量条件也进行了总结。

红外热像仪；辐射温度；实际温度；n值

引言

器件的可靠性与器件的温度有密切的关系。在器件的试验、使用和失效分析过程中，人们十分关心器件温度分布。

器件表面指定位置温度或温度分布一般用红外热像仪进行测量。红外热像仪测温时，要对测量温度和实际温度的关系进行标定，有时还要计算发射率。

我们在用恒温台标定温度时，对如何测量真实温度的细节进行了深入探讨，特别是指数n的取法，感觉很复杂。本文是一些探讨结果。

1 红外热像仪的测温过程

器件用红外热像仪由样品台、探测器固定及调焦支架、红外探测器、光学系统、信号处理系统和显示记录装置等组成。

我们的红外探测器由薄膜淀积热敏电阻构成。红外线通过光学系统聚焦到探测器像元阵列上。当像元接收一定带宽的红外辐射时，其阻值会变化。阻值的变化通过惠斯通电桥而变换为电信号。后续电路对这些原始电信号进一步放大和处理后送至显示器上变成灰度值，形成该目标温度分布的二维可视图像。每种灰度又用伪彩色代替在显示器显示。从而得到图像灰度和物体温度之间的对应关系，实现了测温。

2 物体实际温度与红外热像仪辐射温度的关系

2.1 热像仪常用公式

热像仪基本公式（1）是根据黑体辐射基本概念和定律、光能量度量方式、灰度近似、探测器光谱响应度[1]这些知识，并取探测器接收到的能量为目标自身辐射、环境反射辐射和大气辐射能量的和而推导出来的。笔者推导的结果与资料[2]的结果一致，推导过程从略。

其中

将（2）代入（1）得

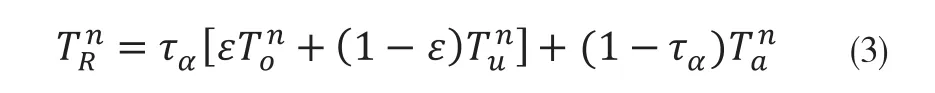
这就是热像仪常用公式（1）、（3）的来历及指数n的出处。C和n在一定条件下也是常数，由实际测量结果计算拟合而得，后面将详细说明。

2.2 热像仪常用公式的简化

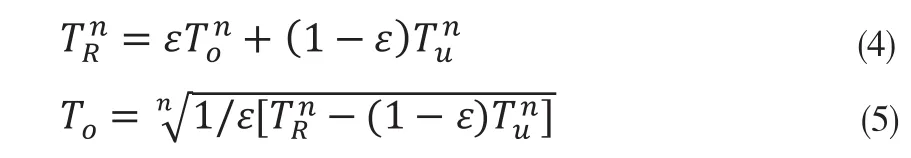
热像仪在洁净化间中使用，可认为是一个有电磁屏蔽的等温环境，周围环境物体温度和大气温度相同，所以可取，式（4）变为

用式（9）及（7）相互参照，能使ε的取值更合理。

如果取n=4，则

式（6）、（7）、（9）及（10）就是计算真实温度和发射率的常用公式。

但是，假若n未知，则ε也算不出来，因此需要知道n值。

3 n值估算方法

任意两式相除，比如

取对数

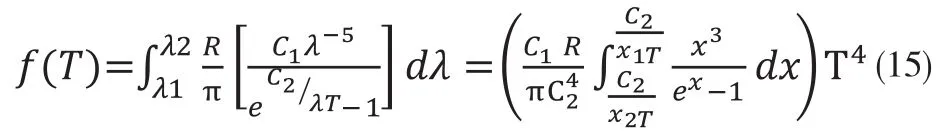
此时式（15）变为

在λ包括了0～∞的所有波长的情况下，从式（15）可得出

σ为斯蒂芬-波尔兹曼常数。

从以上演算可知，常数C与温度范围、波长范围、探测器的光谱响应度都有关系，n可以取4，但C并不总是常数。

换句话说，在n取4时，式（2）成立，但C仅在一定的温度范围和波长范围内有效，超出范围要重取C。

3.3 n值的变化

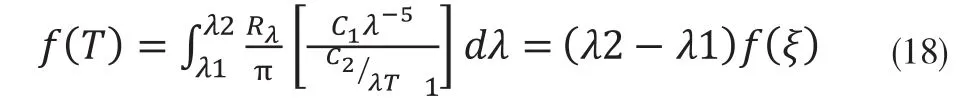
对于InSb探测器，其探测波长范围一般在3～4.7um范围，取ξ=3.85um，在27℃～100℃温度范围，n在10.6～12.2范围，且温度范围越高n越小，积分区间化得越细，越应该更精确，但都在10左右。

对于HgCdTe（8～13um）探测器，在27℃～100℃温度范围，也用上述方法进行计算，约4.09。

的窄波长范围内，n近似为5，在长波或高温区域，用瑞利—金斯公式估算，n近似为1。其实，在目标温度很高时，从式（3）可以得出，近似为，与n没什么关系了。

可见，n会变化，n与探测器的探测波长范围有关，也与温度范围有关。在一定温度范围和探测波长范围内，（2）成立。

3.4 不同n值下的发射率ε计算结果分析

如第2.1节所述，对于一个性能稳定的固体，在窄波长及窄温度范围内，发射率ε可视为常数。表1的ε计算结果与真实情况不同，说明n取值有问题。

3.5 n取4的条件

式中，ξ是λ1与λ2之间的一个数。

令常数：

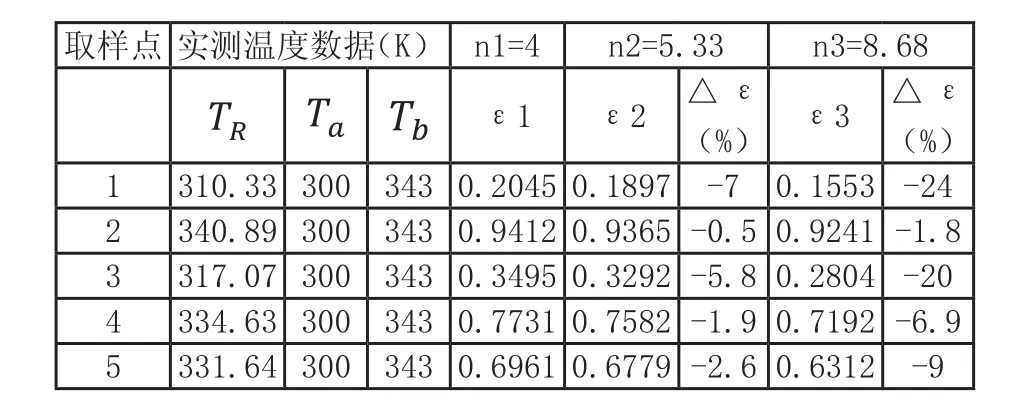
表1 不同n值对应的发射率和变化量

上述结果再一次表明，n可以取4，C也是常数，但C与波长范围和温度范围都有关系。

所以，我们今后在试验中的n就取4，但同时要注明波长和温度范围，也就是C和n是有匹配关系的，要连带考虑。

4 问题的解决方法

由上述可见，n的取值很困难。最好能避开n值和发射率ε。

可选的方法是将器件恒温标定。将温度区间尽可能细分，得出器件上关注位置的实际温度与辐射温度的查找表，记录标定条件（如环境温度、焦距、标定位置等），将其复制到实际测试过程中，再用查找表来查找实际温度。

在测量板级产品的器件温度分布时此法效果较好。因为器件体积大，表面材料种类相对少、面积大，容易标定。还可直接输入已知发射率数据测温。

但IC表面介质和硅材料对于红外线是透明的，又是多层金属布线工艺，微观结构不同，其表面的发射率就不同。但IC结构太多，只能选择有代表性的少量点来标定，会漏掉一些位置。标定分立器件比较要容易。

所以红外热像仪比较适用于IC的失效分析。因为只要知道关注点的相对温度找到热点就行，不必精确测温。

在计算发射率时，可取n为4，用若干个点的标定数据按式（10）来计算发射率，取其平均值。再用式（8）取任意温度组合再来验证和确定ε和n值。

如果要精确测IC表面的温度分布，参考3.4节，芯片表面涂覆厚的高发射率绝缘材料是一个不错的选择，GJB 548的方法就是如此。这时温度分布与芯片表面结构无关，但要先记录芯片形貌来做定位参考。

5 结束语

式（6）、（7）、（9）、（10）是我们常用的计算公式。但这些公式导出时作了如下假定，在使用公式时要尽量与这些假定协调一致：

1）假定被测物体为灰体，遵从朗伯定律。这就要求我们在使用热像仪观察物体时要聚好焦，使探测器与被测物体表面（或观测点）尽量平行。

2）假定了大气透射率为1，也就是没有衰减，所以被测物体与热像仪距离要尽可能缩短，空气湿度别太大。

3）假定了大气环境温度和外界物体的温度不变，都等于大气温度，因此热像仪的使用环境要稳定可控，周围没有大辐射源，起码要避开实验室的进出风口。

4）假定了发射率、吸收率、透射率等是常数，所以推导的公式只适用于较为稳定固体材料，且在窄的温度和波长范围内使用。

5）指数n的选择要根据具体的探测器来选择，如果设备厂家未告知，则要重新标定，不能乱取。n可取4，但要注意C在一定条件下是常数，条件变了则C也要变，C与n一样，与波长范围、温度范围、探测器的光谱响应度有关，也与光学透镜、滤光片等光学器件有关。

热像仪用于器件的失效分析是不错的选择，测板级器件温度分布也有很好的效果，但要测IC芯片表面温度分布时要先进行精密的温度标定，操作困难。芯片表面精确温度分布要靠涂敷高发射率材料来实现。

[1]姚启钧.光学教程.第三版[M].北京：高等教育出版社, 2002.

[2] 于波，季玉茹，金光熙.红外热像测温中真实温度的计算[J].吉林化工学院学报. 2004,21(1).

李兴鸿，研究员，航天大规模及超大规模集成电路检测和失效分析中心副主任，北京微电子技术研究所封装测试中心总工程师，毕业于华南理工大学半导体物理与器件专业。作者主要研究方向集成电路失效分析。

Inf uence Factors of Temperature Measurement on Devices

LI Xing-hong, ZHAO Chun-rong, ZHAO Jun-ping
（Beijing Microelectronic Technology Institute, Beijing 100076）

According to temperature measurement process and basic formula by using thermograph, we discussed measurement condition, calculated index n, and was considered n as 4. While that constant C and index n have a relationship with wavelength and temperature range, C and n should be matched. Finally, we summarized that test conditions about precision IC temperature distribution.

thermograph; radiation temperature; fact temperature; n value

TN4

A

1004-7204（2014）04-0006-04