分数维约束下的自适应对消技术研究

杨 振，杨建强

（1.国土资源部海底矿产资源重点实验室，广州 510075；2.广州海洋地质调查局，广州 510760；3.内蒙古煤田地质局勘测队， 呼和浩特 010010）

分数维约束下的自适应对消技术研究

杨 振1，2，杨建强3

（1.国土资源部海底矿产资源重点实验室，广州 510075；2.广州海洋地质调查局，广州 510760；3.内蒙古煤田地质局勘测队， 呼和浩特 010010）

介绍了自适应对消技术的基本原理，分析了自适应对消技术的优缺点，针对一些缺点提出了相应的改进方法。由于常规自适应对消技术是通过迭代技术实现的，需要迭代一定次数后才能确定最佳参数，所以在信号起始位置和有效信号尾部收敛效果不好，从而影响滤波效果。引入hausdorff维数来约束地震信号，首先求取原始地震信号的hausdorff维数谱，利用有效信号与随机噪音维数的不同，将有效信号以外的随机噪音滤除，并将自适应对消中的参考噪声对应位置的随机噪音去除；然后将更新后的地震信号和参考噪声进行自适应滤波，从而得到一个优化的自适应对消滤波器。

自适应噪声对消；分数维；LMS；NLMS

0 引言

“三高一准确”是地震资料最理想目的。地震数据如果没有较高的信噪比，高保真、高信噪就无从谈起。通过滤波去除噪声是提高信噪比的主要途径。多年来，众多学者提出了许多不同类型的去噪方法。

本文引入的分数维是根据不同信号的维数差异将其区分开来。Boschetti等人根据分形理论，利用地震记录中的维数变化检测地震信号的初至时间[1-2]。常旭等人给出了一种基于广义分维的信号初至估计方法[3-4]。自适应对消技术是利用噪声模型，通过迭代运算将地震记录中的噪声消除。魏巍、刘学伟等人将自适应噪声对消技术成功的应用到了单频干扰的消除[5]。苗文广利用对消技术在折射波的去除上取得了较好的效果[6]。

因此我们利用分数维的这一特性与传统的自适应对消技术进行结合，首先通过分数维将地震数据和噪声模型中的随机噪音滤除，然后再进行自适应噪声对消。由于引入了分数维压制随机噪音，有效的规避了自适应对消技术所带来的信号初始位置及有效信号位置的后部震荡问题。本文通过理论数据和实际数据系统验证了分数维约束下的自适应对消技术的可行性。

1 自适应对消技术原理

自适应噪声对消技术，是通过一些方法（低通滤波、预测模型等方式）获得初始噪声模型x（n），对该模型进行迭代运算得到噪声数据y（n），最终用d（n）减去y（n）得到消除噪声后的数据。如图1所示[7]。

图1中所示，误差信号为

上述误差信号的均方误差E[e2（n）]达到最小，其表达式为

我们定义ε=E[e2（n）]，当均方误差ε达到最小时，我们就可以得到最终的噪声数据。

由于直接求取误差信号比较困难，通常我们采用最小均方算法来实现自适应滤波器的迭代，当输入信号的振幅过大或过小时，会造成滤波器不稳定，因此我们采用较为常用的NLMS算法[7]。

图1 自适应噪声抵消器的一般结构Fig.1 General structure of self-adapting filter

1.1 两种算法对比

当输入信号的振幅过大或过小时，LMS算法会造成滤波器不稳定，如图2所示，原始输入信号为

同时，随机噪声为五倍单位随机噪音。如图2所示，当输入信号振幅较大时，会造成滤波器的不稳定，从而影响到滤波效果。因此我们使用NLMS算法，可以有效的避免这种问题的发生。如图3。

由图2和图3可以看出，NLMS算法相较于LMS算法具有很大的优越性，能够有效的避免当输入信号振幅过大过小造成的滤波器不稳定问题。

2 自适应对消数值模拟算例

利用NLMS算法针对模拟地震数据进行仿真实验，如图4所示。

图2 运用LMS算法的自适应对消实验Fig.2 The adaptive cancellation experiment by LMS algorithm

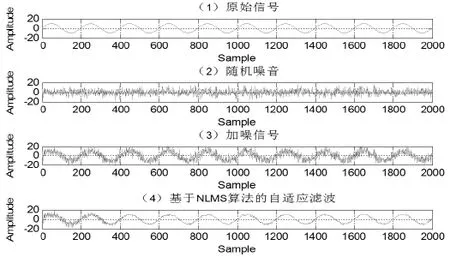
图3 运用NLMS算法的自适应对消实验Fig.3 The adaptive cancellation experiment by NLMS algorithm

图4 运用NLMS算法的自适应对消实验Fig.4 The adaptive cancellation experiment by LMS algorithm

通过图4分析可知，基于NLMS算法的自适应对消技术能够较好的滤除噪声，但在信号序列的初始位置及有效信号位置的后部会产生震荡，为了避免这种震荡，我们由此引入分数维（hausdorff瞬时维数）来约束噪声模型[2-4]。

图5为图4中所示的原始信号。图6为图4中的加噪信号。选取合适的参数，计算图6的Hausdorff瞬时维数，如图7所示。

利用NLMS算法的自适应对消技术能够有效的消除随机噪音，即图8所示，我们可以看出，在信号的开始和有效信号所在的尾部有震荡。为此我们根据图7所示的维数曲线，基于Hausdorff维数的差异，将有效信号范围之外的随机噪音滤除，并将输入参考噪声中对应部分的随机噪音去除，将更新后的加噪数据和参考噪声进行自适应滤波可得到图9所示的滤波结果。

从图9可以看出，该滤波效果与原始信号图5大致相同。基于上述仿真实验结果可以看出，Hausdorff维数约束下的自适应对消技术优化了传统的自适应对消算法[12]。

图5 原始信号Fig.5 Original signal

图6 加噪信号Fig.6 Noise signal

图7 图6的Hausdorff维数Fig.7 The hausdorff dimension of the data in the fig.6

图8 图4中第四个曲线Fig.8 The fourth curve in the fig.4

图9 基于Hausdorff维数约束下的自适应对消技术实验Fig.9 The adaptive noise cancellation experiment based on the hausdorff dimension constraint

3 自适应对消实测数据验证

图10为某地区实测的地震数据 （Z分量）。对图10所示地震数据利用低通滤波得到一个噪声数据。如果利用所得到噪声数据直接进行去噪，是不可以的。

我们利用图10所示的原始数据和图11所示的噪声数据进行自适应对消滤波。其结果如图12所示。

对图10和图11所示数据运用第二章节所实验的方法，可以得到图13所示的结果。

通过图12和图13的振幅谱对比可以看出，分数维约束下的自适应对消技术能有效的优化传统的自适应对消技术。

4 结语

从 1.1节中所进行的仿真实验可以看出，NLMS算法相较于LMS算法具有很大的优越性，能够有效的避免当输入信号振幅过大过小造成的滤波器不稳定问题。

从第三章节的实验中可以看出，可以将传统滤波方法所得到的噪声作为参考噪声输入，进行Hausdorff维数约束下自适应对消技术滤波，从而优化传统滤波方法的效果。

图10 左图为实际地震数据（Z分量）；右图为其振幅谱Fig.10 Actual seismic data on the left(Z component);its amplitude spectrum on the right

图11 左图为低通滤出的噪声（10 Hz以下）；右图为其振幅谱Fig.11 The low-pass filter data on the left(under 10 hz);its amplitude spectrum on the right

图12 左图为自适应对消滤波结果；右图为其振幅谱Fig.12 The adaptive cancellation filter result on the left;its amplitude spectrum on the right

图13 左图为自适应对消滤波结果；右图为其振幅谱Fig.13 The adaptive cancellation filter result on the left;its amplitude spectrum on the right

本文所引入的分数维约束下的自适应噪声对消技术，能在一定程度上避免自适应噪声对消技术带来的信号初始位置及有效信号位置后部的震荡问题，并从理论数据和实际数据两方面验证了该方法的可行性。

[1]牛滨华，孙春岩，张中杰，等.多项式Radon变换[J].地球物理学报，2001，44（2）：263-271.

[2] Boschetti F，Dentith M D，List R D.A fractal-based algorithm for detecting first arrivals on seismic traces[J]. Geophysics,1996，61（4）：1095-1102.

[3]常旭，刘伊克.Hausdorff分数维识别地震道初至走时[J].地球物理学报，1998，41（6）：826-832.

[4]常旭，刘伊克.地震记录的广义分维及其应用[J].地球物理学报，2002，45（6）：839-846.

[5]魏巍，刘学伟.自适应噪声抵消技术的仿真与应用研究[J].计算机仿真，2009，26（2）：358-361.

[6] 苗文广.频率域自适应滤波技术及其应用[D].吉林：吉林大学，2005：20-29.

[7] 曹斌芳.自适应噪声抵消技术的研究[D].湖南：湖南大学，2007：6-38.

[8] 牛滨华,沈操,黄新武.波动方程多次波压制技术的进展[J].地球物理学进展，2002，17（3）：480-485.

[9]Mandelbrot B B.The Fractal Geometry of Nature[M].San Francisco：W.H.Freeman and Company，1982.

[10]陈波.自适应滤波技术研究及其应用[D].武汉：武汉理工大学，2010.

[11]陈莉.自适应滤波算法与应用研究[D].西安：西安电子科技大学，2006.

[12] 杨振.基于分数维的自适应滤波去噪方法研究[D].北

京：中国地质大学，2012.

Study of Adaptive Cancellation Technology Based on the Fractal Dimension Constraint

YANG Zhen1，2，YANG Jianqiang3
（1.Key Laboratory of Marine Mineral Resources，Ministry of Land and Resources，Guangzhou 510075，China；2.Guangzhou Marine Geological Survey，Guangzhou 510760，China；3.Survey Team of Coal Geological Bureau of the Inner Mongolia Autonomous Region，Hohhot 010010，China）

This article describes the basic principles of the adaptive cancellation technology,analysis the advantages and disadvantages of the adaptive cancellation technology,and proposes some corresponding improvement methods about the shortcomings of the adaptive cancellation technology.Since the conventional adaptive cancellation techniques are realized by iteration and need some times to make sure the best parameters, so the starting position of the signal and the tail of the effective signal are not well convergence，thus affectingthe filtering effect.The paper used the hausdorff dimension constrain the seismic signal.Firstly,the paper computes the hausdorff dimension of the original seismic signal,and then filters the random noise beyond of the effective signal and the random noise at the relative position in the referenced noise based on the difference of the hasusdorff dimension about the effective signal and random noise;secondly，the paper updates the seismic signal and referenced noise to be adaptive filter，and gains an optimized adaptive cancellation filter.

Adaptive noise cancellation；Fractal Dimension；LMS；NLMS

TN97

A

1001-8662（2014）03-0076-06

10.13512/j.hndz.2014.03.013

杨振，杨建强.分数维约束下的自适应对消技术研究 [J].华南地震，2014，34（3）：76-81.[YANG Zhen，YANG Jianqiang.Study of Adaptive Cancellation Technology Based on the Fractal Dimension Constraint[J].South china journal of seismology，2014，34（3）：76-81.]

投稿日期：2013-12-25

国家专项项目课题（GZH201200508）

杨 振（1986-），男，硕士，工程师，主要从事海洋地震资料的处理与研究工作.

E-mai:542644088@qq.com.