基于航路规划的飞机节油问题研究

谷润平，陈 慧

（中国民航大学空中交通管理学院，天津 300300）

基于航路规划的飞机节油问题研究

谷润平，陈 慧

（中国民航大学空中交通管理学院，天津 300300）

以燃油成本最小为目标，综合考虑航班的频率限制、机型的市场需要、航路对机型的限制以及机队飞机的可用时间限制等因素，确定航空公司运营的各条航线与现有机队中各机型的最优组合，实现机型航班的优化配置节省燃油成本。并就该问题建立整数规划模型，通过算例对模型的应用进行分析和评价。

航班优化；节油；整数规划

近年来，随着中国经济的腾飞，民航事业迅速发展，航空公司想在激烈的市场竞争中脱颖而出，需要面临的问题之一就是进行合理的机队规划[1-2]。然而，许多航空公司面临的现状是公司机队已基本成型，但随着新航线的开辟、市场需求的变动，航班需要随之调整，因此航空公司急需解决是航班机型分配问题。与此同时，中国民航业燃油消耗量以年均约12%的速度增长。2011年中东局势日益紧张，国际原油价格飙升。加之中国航油经营的特色体制，使得燃油费用成为国内多数航空公司的最大成本项目[3]。因此，节油减排已不仅是环保问题，更是关系航空公司持续发展的重要影响因素。

本文旨在将燃油成本降至最低，着重考虑航空市场需求、航班频率限制、航路机场适航限制及航空公司飞机数量限制等因素[4]，通过建立数学规划模型，为航空公司航班优化决策提供依据。采用的规划方法简化了模型结构，在应用过程中快速抓住关键点，减少预测需要的信息量，同时还能满足机队规划应具备的市场适应性、灵活性要求，为航空运营者寻求机型与航班的优化配置以降低燃油成本提供了一种科学分析工具[5]。

1 节油优化模型构造

1.1 目标函数

假设航空公司有m条航线，有n种机型；或者航空公司机型较多，进行座位级计算简化后，航空公司有m条航线应使用同一座级的飞机，并且该座级的备选机型共有n种，单位时间（1天）内第i种飞机在第j条航路上往返飞行的次数为xij（i=1，2，…，n；j=1，2，…，m），根据首要考虑的节油因素，建立以下的目标函数

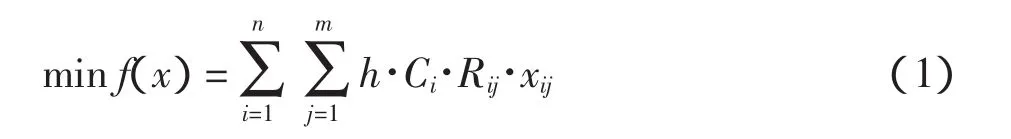
其中：h为航油价格（元/kg），Ci为机型i平均耗油率（kg/h），Rij为机型i在第j条航线上往返一次的平均飞行时间。目标函数是为每个航班安排具体的执行机型，以实现机队燃油消耗最小。

1.2 约束条件

1.2.1 频率（航班量）限制

其中：Qj为第j条航线上单位时间航班的最小频率，根据客货物需求量及政治、经济、地理位置等因素确定；Pj为第j条航线上单位时间航班的最大频率，受航班飞行时间和过站时间的限制，每条航线上的航班总量不大于该航线上所允许安排的最大航班量。

1.2.2 客流量限制

其中：机型i的座位数为Seati；计划满载因子为η；j航路预计单位时间能够实现的客流量上限为Demandj。式（3）反映了每条航线上可提供座位数不应小于总客流量。

1.2.3 机队有效时间限制

其中：Timei表示机型i单位时间内可执行任务的总时间。式（4）表示机型i单位时间内实际执行任务时间不应大于机型i单位时间内可执行任务的总时间。

1.2.4 机场及航路限制

由于设备条件或地理因素（高原高温机场）等限制，部分机场不允许某些机型起降，或者某些航路距离大于飞机最远航程，因此有

1.3 模型算法说明

这是一个整数规划模型，可以采用分支界定法求解[6]，得到燃油成本最小方案。

2 模型应用

已知某小型航空公司机队有3种机型，每种机型的数量、耗油率、可提供座位数、单位时间内可执行任务时间，如表1所示。

表1 机队配置相关数据Tab.1 Fleet configuration data

该公司运营航线30条，机型i在航路j上的往返时间、航路j的航班量限制、j航路预计单位时间能够实现客流量的上限，如表2所示。计划满载因子为0.8，由于机场原因限制，X305=0，X319=0。燃油价格0.5元/kg。

表2 航线相关参数Tab.2 Route-related parameters

2.1 原分配方案

根据公司原有分配方案，每条航线由何种机型执行及执行次数配置方案，如表3所示，目标函数值为234 000元。

表3 原方案航班配置Tab.3 Original scheme of flight configuration

2.2 优化方案

根据上节节油优化模型，应用LINGO规划软件求出优化解：目标函数值214 030元。每条航线具体由哪种机型执行及执行次数具体配置方案，如表4所示。

表4 优化方案航班配置Tab.4 Optimization scheme of flight configuration

2.3 结果分析

从目标函数值可明显看出，优化航班配置后，每天可节省燃油成本19 970元，则1年可节省约729万元，节约率约8.5%，根据新方案运行将使整个航空网络运营的燃油成本更低。

当航空公司机队规模越大，运营航路越多时，应用该模型优化的效果越明显[7]。

3 结语

本文对以节省燃油成本为目标的航班规划建立了整数规划模型，通过模型优化可为航空公司节省更多燃油成本且效果明显。用这种算法优化公司航班，既能满足市场需求，又可节省大量资金[8]。

本文构造的模型通用性较强，不仅考虑了航班的频率限制、市场客流量限制、航路对机型的限制以及机队的可用时间限制等因素，在具体的运用过程中还可以灵活掌握，根据实际情况进一步扩展或减少限制条件，如航空公司空勤人员数量对航班配置的限制、院校训练飞行可以不考虑客流量限制，甚至修改目标函数，如航班运行总成本最低或总收入最大，以调整最优解或满意解范围。

[1]彭语冰，张永莉，张晓全.机队规划模型的建立及其应用[J].系统工程理论与实践，2001（6）：100-103.

[2] DR PETER P BELOBABA.Airline Fleet Planning Models[EB/OL].（2006-4-10/2008-11-20）[2013-02-01].http：//www.core.org.cn/OcwWeb/Aeronautics-and-Astronautics/16-75JSpring-2006/LectureNotes/index.htm.

[3] 罗 杰，张雄旗，李国胜.基于燃油成本最小化的机队规划模型[J].应用科学，2009（18）：148.

[4] 闫克斌，孙 宏，史虹圣.飞机选型问题数学模型的建立[J].飞行力学，2005，23（4）：82-85.

[5] TREVETT J C.Fleet planning models[J].The Aeronuatical Journal，1983，87（863）：88-94.

[6]官建成.整数型机队规划模型及其应用[J].北京航空学院学报，1987（2）：67-75.

[7]TIMOTHY L JACOBS，BARRY C SMITH，ELLIS L JOHNSON.Incorporating network flow effects into the airline fleet assignment process[J].Transportation Science，2008，42（4）：514-529.

[8] ABARA J.Applying integer linear programming to the fleet assignment problem[J].Iterfaces，1989（19）：20-28.

Fuel conservation research based on route planning

GU Run-ping，CHEN Hui
（College of Air Traffic Management，CAUC，Tianjin300300，China）

The objective of optimization model is to minimize the airlines’ fuel cost.Several factors are considered to confirm the optimal composition of airplane types and fleets and to achieve fuel conservation，such as flight frequency on each air route， traffic demand of certain airplane type， route restrictions with the airplane types and the available time of fleet.One mathematical programming model is introduced； meanwhile， the analysis and evaluation of the model applications are presented with example.

flight optimization；fuel conservation； integral programming

F560.1

A

1674－5590（2014）02－0033－03

2013-02-06；

2013-04-10

谷润平（1971—），男，陕西靖边人，副教授，硕士，研究方向为飞机性能.

（责任编辑：杨媛媛）