斜交空心板梁极限承载力数值模拟分析及计算方法研究
2014-05-28龙浩军欧阳祥森
龙浩军,欧阳祥森
(1.湖南省交通规划勘察设计院,湖南 长沙 410008; 2.湖南工程学院,湖南 湘潭 411104)
0 引言
斜交空心板桥因其结构轻巧、施工简便,特别是建筑高度远低于相同跨径的其他梁式体系的桥梁,所以在斜交桥中成为人们的首选桥型。但是受到斜交角度的影响,对斜交空心板梁进行受力分析时不能将斜交板梁视为简支梁,斜交梁受力的复杂程度要远大于正交梁。此外由于斜交空心板梁截面挖空率大,荷载作用下除了表现出斜梁的受力性能外,还会表现出只有箱型截面才会出现的的翘曲、畸变等特性。国内外针对斜交梁桥的设计及计算方法进行研究的文献较多,而对斜交空心板受力分析及设计计算中的许多关键问题仍然认识模糊,这使得斜交空心板的设计十分不便。为加深对斜交空心板梁受力性能的认识,本文建立不同斜交角度空心板梁有限元模型,在考虑材料非线性的基础上对斜交板梁的抗弯极限承载力进行数值模拟计算,通过数值模拟的方式确定各种斜交角度空心板梁的极限承载力、关键截面的破坏形态,以此来弥补无法通过实物的破坏性试验来获得相关特性的缺陷。根据数值模拟所确定的关键截面的破坏规律,结合平截面假定以及材料的本构关系提出斜交空心板梁的极限承载力计算公式,以供设计人员参考使用。
1 不同斜交角度空心板梁计算分析模型的建立
分别建立斜交角度为 15°、30°、45°的斜交空心板梁有限元模型进行数值模拟计算,考虑混凝土、预应力筋以及普通钢筋的材料非线性,通过试算和分析确定混凝土材料和钢筋材料的本构关系和破坏准则,以确保计算分析的正确和非线性求解的快速收敛。通过对各种斜交角度的斜交空心板梁的计算机数值模拟,对斜交空心板梁的受力进行全过程描述,确定板梁的主要受力阶段,为斜交板梁极限承载力计算公式的推导提供理论依据。
1.1 材料的本构关系
对结构进行非线性分析,结构材料本构关系确定的准确与否是分析成败的关键。本文在考虑混凝土以及钢筋的本构关系时做如下假定:①混凝土材料的本构关系分阶段考虑,混凝土未开裂之前,采用线性本构关系;开裂后,采用非线性本构关系。②模型中预应力筋的σ-ε 关系采用双直线,普通钢筋采用理想的弹塑性σ-ε 关系。混凝土与钢筋材料具体的本构关系设定见文献[1]。
1.2 预应力混凝土斜交空心板的非线性有限元模型
本文以某标准跨径为30 m 的预应力混凝土斜交空心板梁为工程背景,单片空心板板宽1.59 m,板高1.40 m,采用C40 混凝土,标准强度fpk=1 860 MPa 的预应力筋。为简化建模过程,将空心板梁的横断面进行简化,简化后空心板梁横截面如图1所示。以该斜交空心板为基础,采用相同的截面形式,分别建立斜交角度为15°、30°、45°斜交空心板的非线性有限元模型,对不同斜交角度的斜交空心板做极限承载力数值模拟分析。
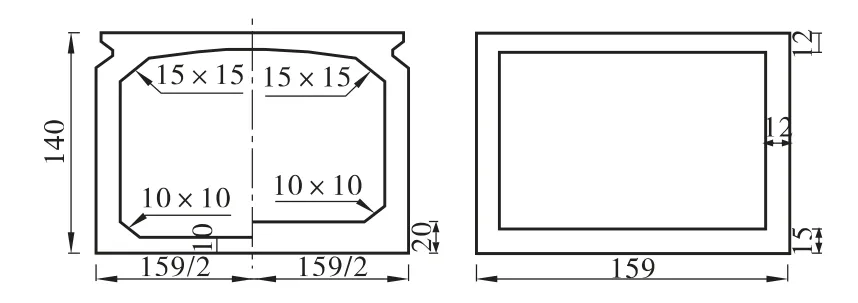
图1 斜交空心板简化图(单位:cm)
通常钢筋混凝土结构的有限元模型有3 种方式[2]:分离式、组合式和整体式。本文在建立不同斜交角度空心板梁时采用分离式和整体式相结合的方法,其中预应力筋用杆单元单元模拟;普通钢筋均匀弥散在混凝土中形成整体式模型,用能切实反映钢筋混凝土受力特性的三维实体单元来模拟。整体模型实体单元将钢筋分布于整个单元中,假定混凝土和钢筋粘结很好,单元视为连续均匀材料,因此钢筋与混凝土对单元刚度的贡献不会分别求出后再组合而是一次求得综合的刚度矩阵,但此时单元的刚度矩阵[D]需用由钢筋和混凝土两部分组合的弹性矩阵,其具体表达式为[3]:
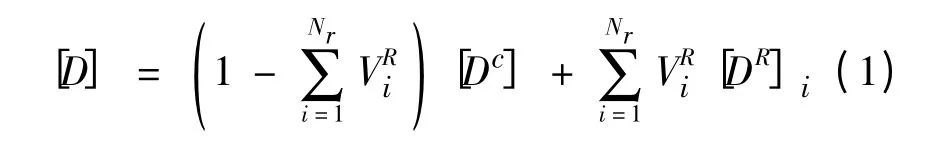
式中:Nr表示单元中加固材料即钢筋的数目(一般最多设置3 个参数即配筋的3 个方向);表示i 方向加固物即钢筋的体积率,即i 方向的钢筋体积配筋率;[Dc]表示混凝土的刚度矩阵;[DR]i表示 i 方向加固物(钢筋)在单元总体坐标系下的刚度矩阵,它可由下式给出:
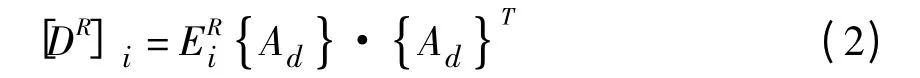
对混凝土实体单元采用了如下基本假定[4]:①只允许在每个积分点正交的方向开裂;②积分点上出现裂缝后,将通过调整材料属性来模拟开裂,裂缝的处理方式采用分布模型;③混凝土在整个受力阶段按各向同性材料考虑;④除开裂和压碎之外,混凝土也会塑性变形,采用Drucker -Prager 屈服面模型模拟塑性行为和应力-应变关系。
根据不同斜交角度空心板梁钢筋的布置情况,将各种斜交角度空心板梁沿板长、板高方向分区、分层,根据实际配筋的情况对不同的区域采用不同的钢筋体积配筋率。在支座处加约束时,考虑节点支承力对结构局部的影响较大,在梁端部反力支撑处处通过调整单元参数模拟钢板单元防止局部压碎。空心板单元离散网格见图2所示。

图2 斜交空心板梁单元离散图
将模型中各个参数调整设定完成后,对空心板梁模型施加约束、施加载荷,采用修正的NEWTON- RAPHSON 求解。
2 不同角度斜交空心板数值模拟计算结果分析
由于斜交空心板梁的非对称性,对不同斜交角度的空心板模型采用对称加载和非对称加载两种方式,通过数值模拟确定不同斜交角度的空心板梁在对称集中力作用和非对称集中力作用下的主要受力阶段以及关键截面发生正截面破坏时受压区应力分布规律,以及受拉区混凝土开裂后中性轴上移后的分布规律。具体加载形式如下:对称加载:在跨中截面顶板两侧对称地加大小相同的集中荷载,如图3;非对称加载:在跨中截面顶板一侧(Y= -0.8 m)施加偏载,如图4。
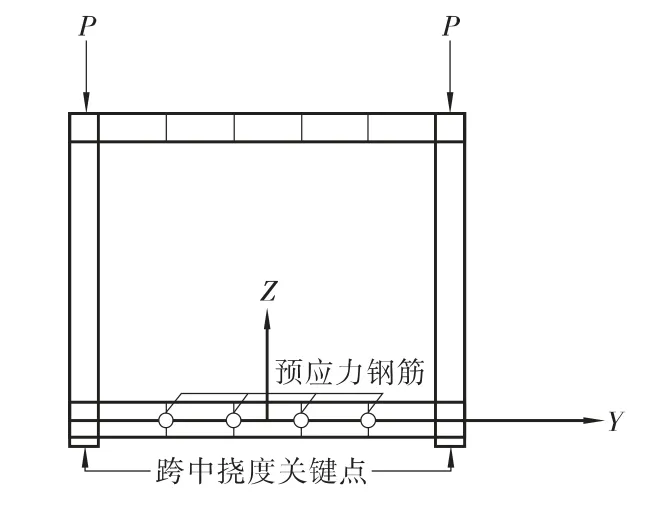
图3 对称加载位置示意图
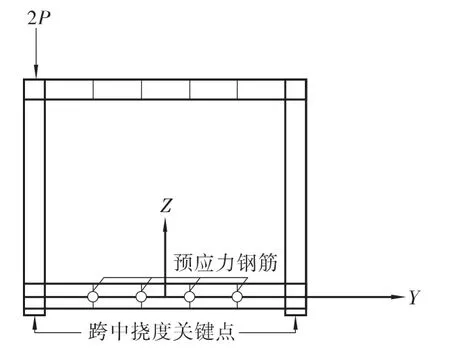
图4 非对称加载位置示意图
在对称荷载作用和非对称荷载作用下,空心板设计关键截面底板关键点P-f(荷载—挠度)曲线、空心板设计关键截面预应力筋节点P-σ(荷载—应力)曲线如图5~图8。同时本文将不同斜交角度斜交空心板梁在对称集中力和非对称集中力作用下破坏时设计关键截面受压区混凝土压碎时混凝土压应力分布情况以及截面破坏时极限应变分布规律绘成曲线,如图9~图14,其中受拉为正,受压为负,“(a)”表示发生正截面破坏时设计关键截面受压区混凝土压应力的分布规律;“(b)”表示发生正截面破坏时截面极限应变的分布情况,图中点划线描述破坏时截面中性轴的位置。
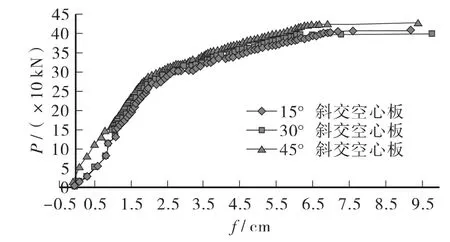
图5 对称荷载作用下板荷载-挠度曲线

图6 对称荷载作用下预应力筋的荷载-应力曲线
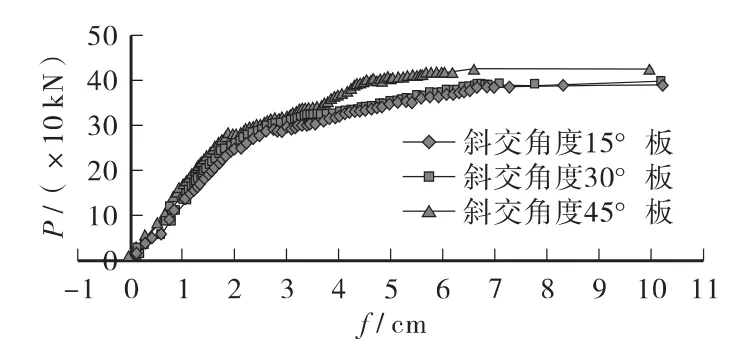
图7 非对称荷载作用下板荷载-挠度曲线
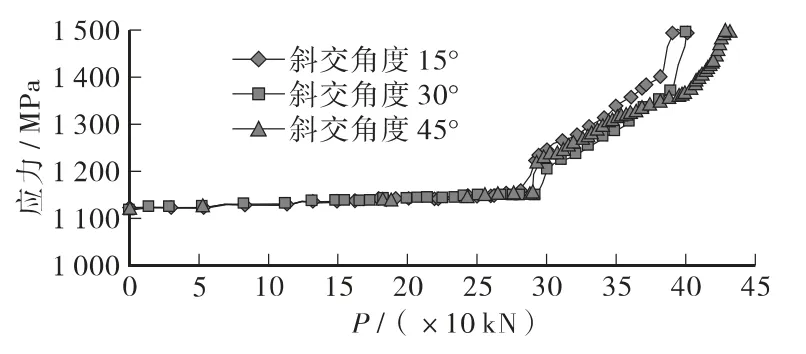
图8 非对称荷载作用下预应力筋的荷载-应力曲线
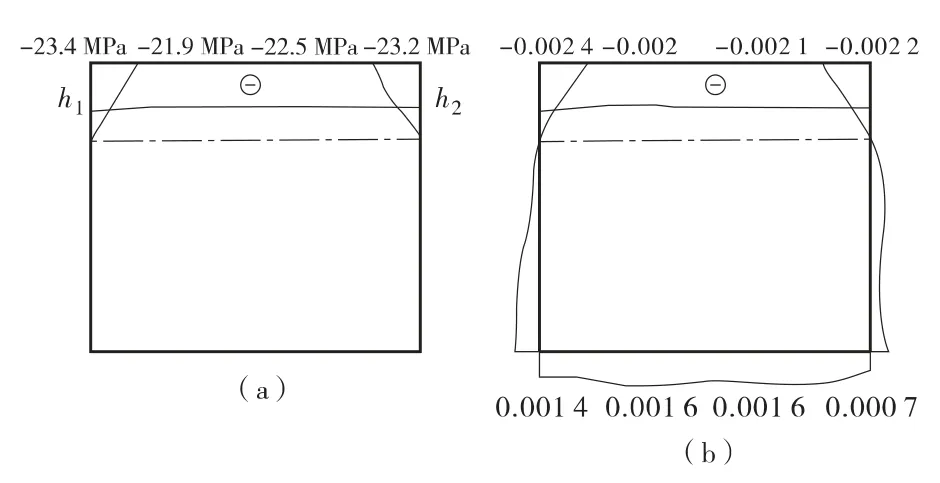
图9 对称荷载作用下15°斜交板破坏时跨中截面应力(a)、应变(b)
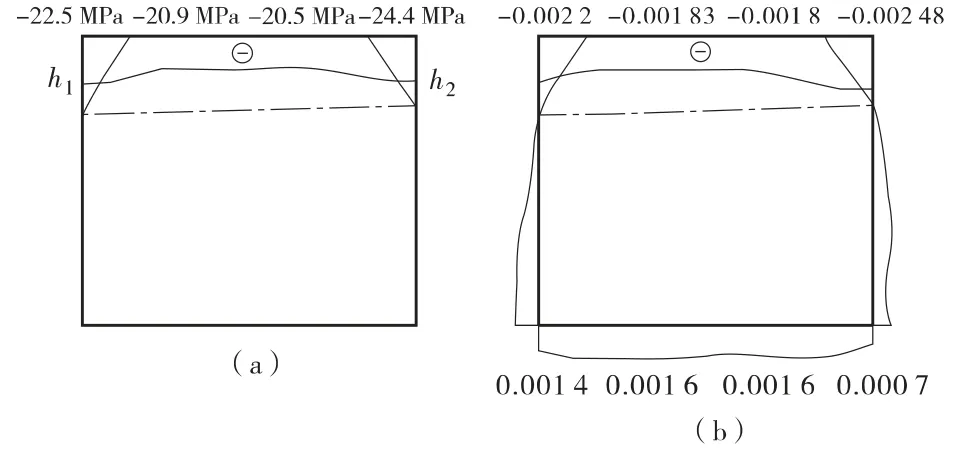
图10 对称荷载作用下30°斜交板破坏时跨中截面应力(a)、应变(b)
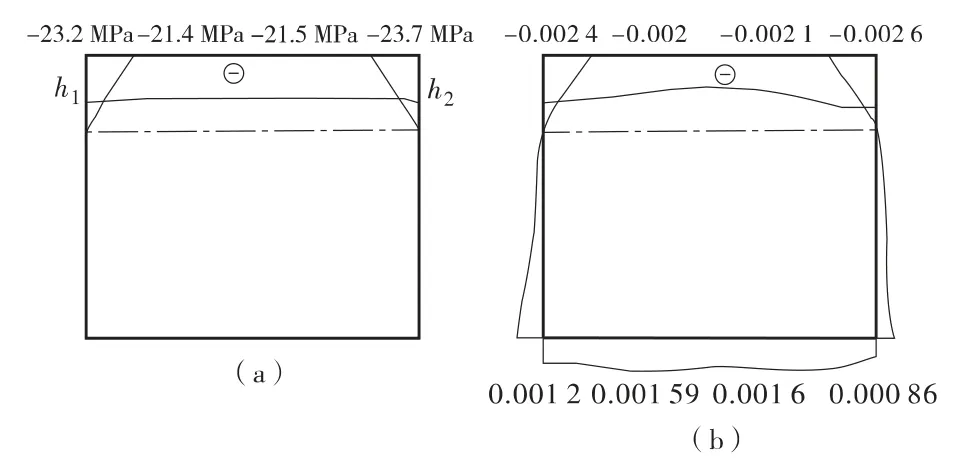
图11 对称荷载作用下45°斜交板破坏时跨中截面应力(a)、应变(b)
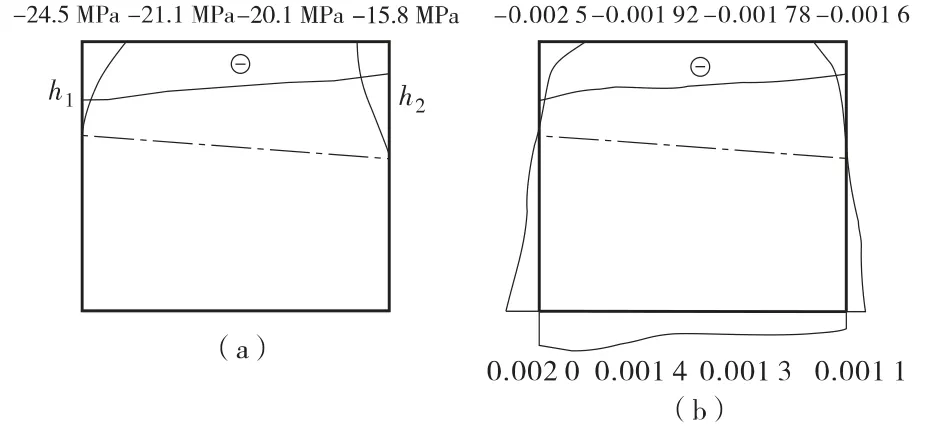
图12 非对称荷载作用下15°斜交板破坏时跨中截面应力(a)、应变(b)
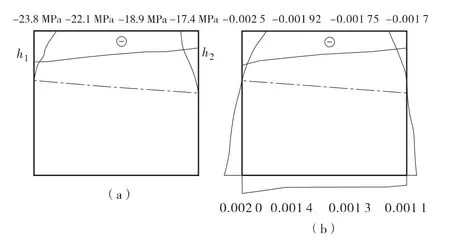
图13 非对称荷载作用下30°斜交板破坏时跨中截面应力(a)、应变(b)
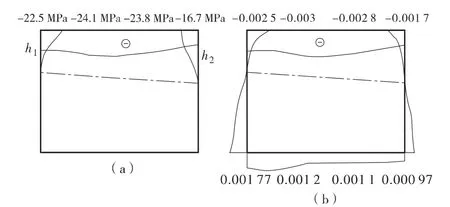
图14 非对称荷载作用下45°斜交板破坏时跨中截面应力(a)、应变(b)
3 不同斜交角度空心板梁的破坏特征与设计方法修正
3.1 不同斜交角度空心板梁的破坏特征
建模采用的约束和支撑条件不同对计算结果有一定的影响,文中建立的不同斜交角度的空心板梁都是采用两点支承的方式,模拟计算完成后可分析总结得出了对称集中力和非对称集中力作用下不同斜交角度空心板梁设计关键截面关键点的P-f 曲线、预应力筋的P-σ 曲线、破坏时设计关键截面应力、应变分布规律,由此可以分析总结出不同斜交角度空心板梁的破坏特征:
1)对称荷载作用时,为防止顶板的局部压碎,集中力施加在腹板的上面。各种斜交角度的斜交空心板在加载至极限荷载时,应力在集中力作用的周边区域较大,有发生局部压碎的征兆;顶板是主要的受压区,其压应力的大小分布不均匀但都接近混凝土抗压强度设计值。板梁中主要承受拉力的预应力筋在受拉区混凝土开裂后应力明显增加,从预应力筋的荷载-应力曲线中可以看到明显的斜率突变现象,预应力筋在达到屈服强度后应力开始保持不变。随着外荷载继续增加,布置于靠近板梁两侧腹板的预应力筋先屈服,之后中间的预应力筋屈服。从荷载-位移曲线可以看出作用荷载相同时,跨中截面关键点的位移量会随着斜交角度的增加略有增加。从荷载-预应力筋曲线可以看出作用荷载相同时,斜交角度越小的板,板中预应力筋的应力越大。
2)在顶板一侧(Y= -0.8 m)的偏心集中力作用下,各种斜交角度的空心板梁会首先在偏心力作用一侧,集中力作用位置附近的腹板受拉区随机的出现细小的垂直裂缝,随着荷载的增加裂缝向上和向两侧面斜向发展,偏心力作用一侧承受拉力的预应力筋会于其他受力主筋屈服,中性轴向偏心力作用一侧偏转。
3)对称荷载作用和非对称荷载作用下破坏时,截面中性轴的高度见表1。从表中数据可以看出对称荷载作用下,斜交空心板梁的中性轴位置会随着斜交角度的增大而略有下移,而在非对称荷载作用下,中心轴的位置却略有上移。
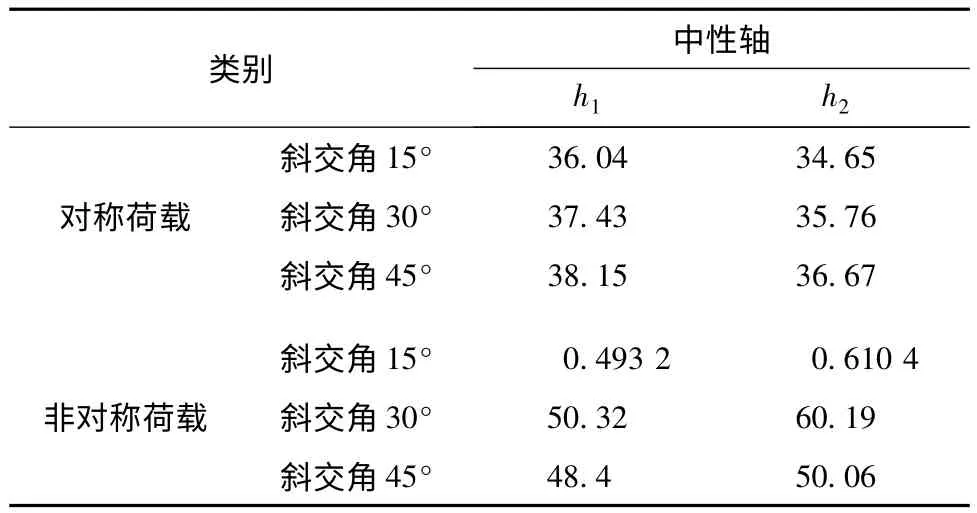
表1 截面中性轴的位置 cm
不同斜交角度空心板梁在对称集中力和非对称集中力作用下受力阶段划分基本相同,但是关键截面的最终破坏形态存在差别,受压区混凝土应力出现滞后现象,说明大挖空率的大截面空心板梁同样存在剪力滞后现象。
3.2 斜交空心板梁强度设计方法修正
根据不同斜交角度空心板梁的破坏形式和破坏特点,对斜交空心板梁的正截面强度计算公式进行讨论并加以修正。
3.2.1 正截面强度计算基本假定
根据以上数值模拟计算分析的结果,考虑到实际工程设计的实用性与准确性的因素,对斜交空心板梁正截面抗弯极限承载力计算公式进行修正时提出以下基本假定:
1)设计关键截面在这个受力过程中都保持平面,无扭曲;
2)计算极限承载力时,不考虑截面底板受拉区以及腹板受拉区混凝土的抗拉强度;
3)主要受力材料的σ-ε 关系:
受压混凝土采用二次抛物线加水平线的σ-ε变关系,预应力筋采用双直线σ-ε 关系,非预应力钢筋采用理想的弹塑性σ-ε 关系;
4)不考虑剪力滞的影响,在受压混凝土的有效工作宽度范围内应力图形采用矩形应力图,进入腹板到中性轴以上区域采用三角形应力分布图形;
5)斜交空心板顶板较薄,混凝土受压区有限,考虑空心板顶板受压区普通钢筋参与受压,并且假定截面破坏时受压区钢筋达到受抗压强度设计值。
3.2.2 斜交空心板梁正截面抗弯极限承载力计算修正
对斜交空心板梁进行正截面抗弯极限承载力计算时,依据截面破坏形态及前述基本假设的规定,对抗弯承载力计算公式进行修正。与以往计算公式[5]相同,依据破坏时截面中性轴的位置,可将空心板梁截面分为两类截面进行计算:第I 类(中性轴在顶板内)和第II 类截面(中性轴延伸至腹板内),其受力示意图如图15所示。
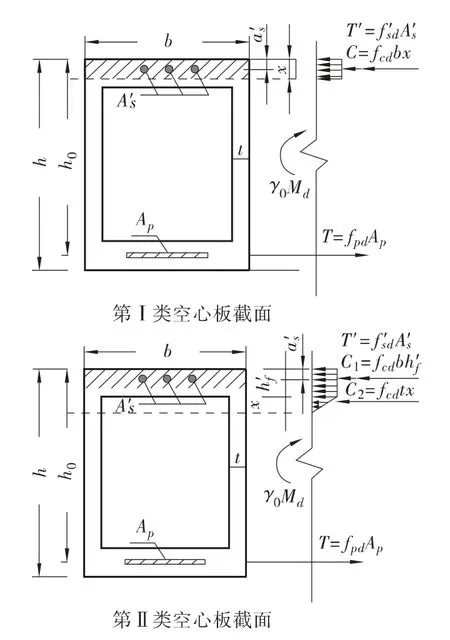
图15 斜交空心板正截面抗弯承载力计算受力示意图
1)第Ⅰ类空心板截面:
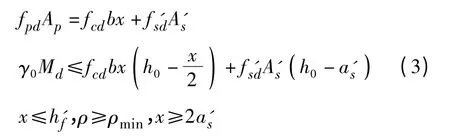
2)第Ⅱ类空心板截面:

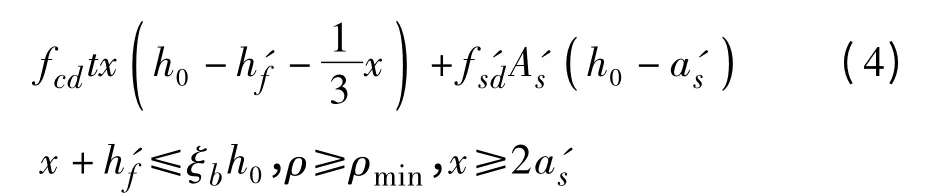
式中:fpd、Ap为受拉预应力钢筋的抗拉强度设计值和截面积;fcd为混凝土轴心抗压设计值;x 为对于第I 类空心板,等效受压区高度;对于第II 类空心板,等效受压区高度减去顶板厚度;b 为空心板宽度;t为单侧腹板宽度;h'f 为顶板厚度;h0为截面有效高度;a's为受压区普通钢筋到受压区边缘的距离;Md为弯矩组合设计值;ξb为相对界限受压区高度,可按文献[6]对应取值;ρmin为截面受拉钢筋最小配筋率,取值查看相关文献[6];γ0为桥梁结构的重要性系数。
运用本文提出的修正过的公式计算所得各种斜交角度空心板梁跨中正截面极限承载弯矩与有限元计算的跨中正截面极限承载弯矩进行对比,结果如表2所示。通过结果对比可以看出,本文对斜交空心板梁的正截面抗弯极限承载力计算公式的修正是合理而且必要的。修正后的公式能更充分地体现对构件材料的充分利用,更符合工程的实际情况。
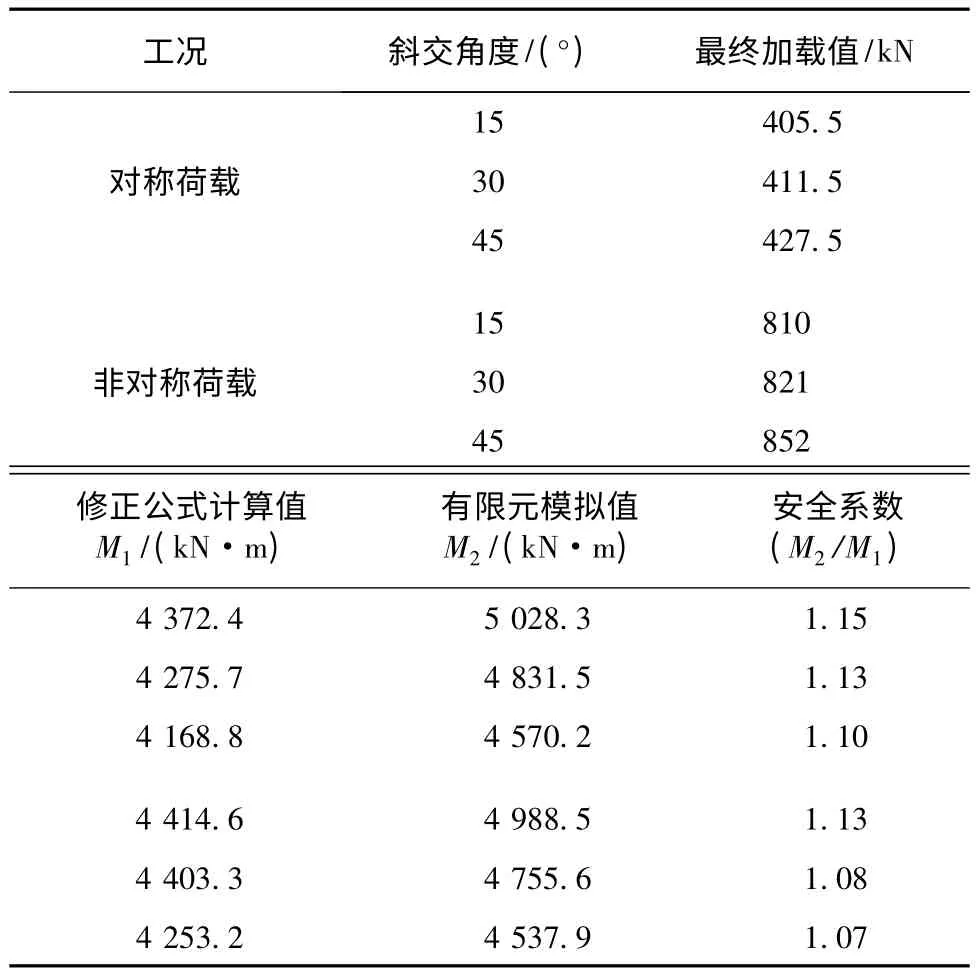
表2 本文提出公式所求得极限弯矩与数值模拟计算所得极限弯矩对比
4 结论
通过对不同斜交角度空心板梁进行的极限承载力模拟计算分析可以得出以下结论:
1)相同跨径不同斜交角度的斜交空心板梁的极限承载力在对称集中力和非对称集中力作用下,其破坏方式、破坏特征、正截面抗弯承载力大小等方面都存在较大差别,设计计算时应特别关注斜交角度对破坏形式以及承载力大小的影响。
2)基于不同斜交角度斜交空心板梁的极限承载力模拟计算分析所得的结果,修正了斜交空心板梁正截面抗弯承载力计算公式,计算公式建立所依据的基本理论以及基本假设与现有预应力混凝土构件的计算方法一致,便于计算。
3)在整个非线性数值模拟分析中未考虑扭矩对空心板跨中挠度、板内预应力筋的影响,而斜交空心板受力是弯剪扭耦合,因此应进一步研究扭矩对斜交空心板破坏的影响。
[1]欧阳祥森.预应力混凝土斜交空心板受力特性分析与极限承载力计算[D].长沙:长沙理工大学,2006.
[2]王新敏.ANSYS 工程结构数值分析[M].北京:人民交通出版社,2007.
[3]刘小燕,颜东煌,张 峰,等.高强混凝土T 梁极限承载力计算与参数分析[J].中国铁道科学,2006,27(1):8 -13.
[4]王勖成,邵 敏.有限单元法基本原理和数值方法(第二版)[M].北京:清华大学出版社,1995.
[5]刘小燕,欧阳祥森.斜交空心板正截面承载力模拟计算研究[J].公路交通科技,2008,25(2):89 -93.
[6]JTG D62 -2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
[7]狄 谨,等.矩形钢管混凝土桁架节点极限承载力研究[J].中国公路学报,2004,17(3):62 -67.
[8]过镇海.混凝土的强度和变形[M].北京:清华大学出版社,1997.
